Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно два решения.
Система равносильна
Пусть — множество точек плоскости
являющихся решением первого
уравнения при условии
Уравнение
задает окружность с
центром в точке
и радиусом
Необходимо, чтобы окружность со
множеством
имела ровно две общие точки. Изобразим положения окружности,
которые нам подходят:
Голубыс цветом изображено множество Все положения окружности, при
которых
и
нам подходят. Здесь
— радиус окружности,
которая касается гиперболы в 1 и 3 четвертях,
— радиус окружности,
которая проходит через точки
и
(общие точки гиперболы и прямой
).
Найдем координаты точек и
В силу симметрии прямой и гиперболы относительно прямой
точки
и
симметричны относительно
Значит, если
окружность проходит через точку
то она проходит и через точку
Так как
то
Следовательно, Тогда нам подходят
Заметим, что в силу симметрии и окружности, и гиперболы относительно
прямой если окружность касается части гиперболы в 1 четверти в точке
то она касается и части гиперболы в 3 четверти в точке
Причем в силу
симметрии и окружности, и гиперболы относительно прямой
точки
и
лежат на этой прямой. Следовательно, пусть
где
— точка
касания окружности радиуса
с гиперболой. Тогда
Тогда исходная система имеет ровно два решения при
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет хотя бы одно решение.
Рассмотрим систему в координатах Тогда графиком неравенства
является круг с центром в точке
и радиусом 3. Рассмотрим
уравнение:
Изобразим графики неравенства и уравнения исходной системы на координатной плоскости:
Системе удовлетворяют точка и все точки отрезка
Следовательно,
где — ордината точки
Найдем
Найдем и
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы одно решение.
Перепишем уравнение в виде
и рассмотрим функцию
Если где
— область значений функции
то исходное
уравнение имеет хотя бы одно решение. Таким образом, нужно исследовать
функцию
Пусть отсюда
Тогда имеем:
Пусть тогда
Нужно найти значения соответствующие
Исследуем функцию Функция нечетная, так как
Производная
Тогда знаки производной на промежутке такие:
Тогда график функции выглядит следующим образом:
Тогда
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет хотя бы одно решение на отрезке
Сделаем замену Тогда
Преобразуем уравнение:
Сделаем замену Если исходное уравнение должно иметь хотя бы
одно решение на отрезке
то новая система
должна иметь хотя бы одно решение на отрезке
Рассмотрим дискриминант уравнения: Так как
то
следовательно,
при всех
Таким образом, уравнение системы имеет ровно два различных корня.
Необходимо, чтобы при хотя бы один корень этого уравнения
удовлетворял условиям
и
Следовательно, как минимум
Поэтому рассмотрим это уравнение при
Пусть — квадратичная функция. Тогда графиком
является парабола, ветви которой направлены вверх и которая пересекает ось
абсцисс в двух точках. Абсцисса вершины этой параболы равна
Следовательно, если и
— соответственно меньший и больший корни
уравнения
то
Следовательно, разве что меньший корень
может лежать в отрезке
Запишем условия, при которых
При найденных имеем
причем выполняется также условие
Следовательно, — нужные нам значения параметра. Тогда
имеем:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых наименьшее значение
функции
меньше 3.
Условие задачи равносильно тому, что неравенство
имеет хотя бы одно решение.
Раскроем модуль, тогда мы получим следующую совокупность, которая должна иметь хотя бы одно решение:
Будем рассматривать параметр как переменную. Построим в системе
координат
множество
решений совокупности. Если некоторая точка
плоскости с координатами
принадлежит этому множеству
то для
исходной задачи это означает, что если параметр
принимает значение
то
будет одним из решений совокупности. Нас просят найти все
такие значения
параметра
при каждом из которых хотя бы одна
из точек вида
,
, принадлежит множеству решений
изображенному на плоскости
Фактически это равносильно тому, что
горизонтальная прямая
имеет хотя бы одну точку пересечения с
множеством
.
Пусть — множество решений первой системы, а
— множество решений
второй системы. Тогда
Множество состоит из всех точек, находящихся внутри окружности с
центром
радиуса 3, лежащих не ниже прямой
Множество
состоит из всех точек, находящихся внутри окружности с центром
радиуса 1, лежащих ниже прямой
Заметим, что обе окружности имеют две точки пересечения и
на прямой
Все прямые, находящиеся между прямыми и
(
— ордината
точки
), имеют со множеством
хотя бы одну общую точку. Следовательно,
все
являются решением задачи.
Найдем Это одна из точек пересечения окружности
с
прямой
Следовательно,
ищется из системы:
Так как то
следовательно,
Значит, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Обосновано получен ответ, отличающийся от верного только включением одной из граничных точек | 3 |
| С помощью верного рассуждения получен
искомый промежуток значений параметра
| 2 |
| Верно сведено к исследованию графически/или аналитически совокупности систем неравенств | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно два различных решения.
Преобразуем систему:
Заметим, что в первом уравнении совокупности не является решением,
следовательно, можно разделить обе части равенства на
и получить тем самым
Назовем множеством множество точек плоскости
которые лежат на
гиперболе
или на прямой
но не ниже прямой
Для того, чтобы понять, как выглядит множество
на плоскости, нужно найти
точки пересечения графиков
и
Для этого нужно решить
систему
Получаем точки
Следовательно, множество на плоскости выглядит следующим образом:
Нужно, чтобы прямая имела две точки пересечения со
множеством
Отметим граничные положения прямой
-
:
-
проходит через точку
тогда система имеет 1 решение;
-
между
и
:
-
система имеет 2 решения;
-
:
-
проходит через точку
тогда система имеет 2 решения;
-
между
и
:
-
система имеет 3 решения;
-
:
-
касается нижней части гиперболы, тогда система имеет 2 решения;
-
между
и
:
-
система имеет 1 решение;
-
:
-
касается верхней части гиперболы, тогда система имеет 2 решения;
-
выше
:
-
система имеет 3 решения.
Определим, при каких точка
принадлежит прямой
Определим, при каких точка
принадлежит прямой
Определим, при каких прямая
касается гиперболы
Тогда уравнение
должно иметь одно решение. Следовательно,
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение или не имеет решений.
Пусть Тогда уравнение примет вид
Рассмотрим две функции и
и исследуем
их.
Функция четная. Ее производная равна
При производная
при
имеем
Следовательно,
является точкой минимума и наименьшее значение функции
равно
Тогда график функции выглядит следующим образом (заметим, что
он при всех
находится в верхней полуплоскости, а также в силу четности
функции
симметричен относительно оси
):
Функция также четная. Ее графиком является корыто, правая ветвь
корыта задается уравнением
дно корыта протяженностью от
до
и высотой
Следовательно,
Значит,
получаем такой график (он тоже при всех
находится в верхней
полуплоскости и симметричен относительно оси
):
Единственное решение уравнение будет иметь, если
а
не имеет решений уравнение при
если при этом правая ветвь
графика функции
не пересекается с правой ветвью графика функции
Проверим, действительно ли при найденных значениях правая ветвь
графика функции
не пересекается с правой ветвью графика функции
Если то графики обеих функций выглядят так:
А уравнение принимает вид
и имеет три решения. Следовательно, нам не подходит.
При правая ветвь корыта имеет уравнение
при
и
действительно выполнено
Следовательно, при
и
Значит, правая ветвь
графика функции
выше правой ветви корыта, а в силу симметрии обоих
графиков относительно оси
и левая ветвь графика функции
выше левой
ветви корыта. То есть при
графики выглядят следующим образом:
Следовательно, в ответ идут
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно два различных решения.
Преобразуем первое уравнение системы:
Сделаем замену Тогда система примет вид
Рассмотрим графики, которые задают оба уравнения в системе координат
Первое уравнение задает окружность с центром в точке
радиуса
Второе уравнение задает «корыто», ветви которого имеют наклон
и
а дно находится на высоте
и протяженностью от
до
Определим траекторию движения центра окружности:
Изобразим на плоскости графики:
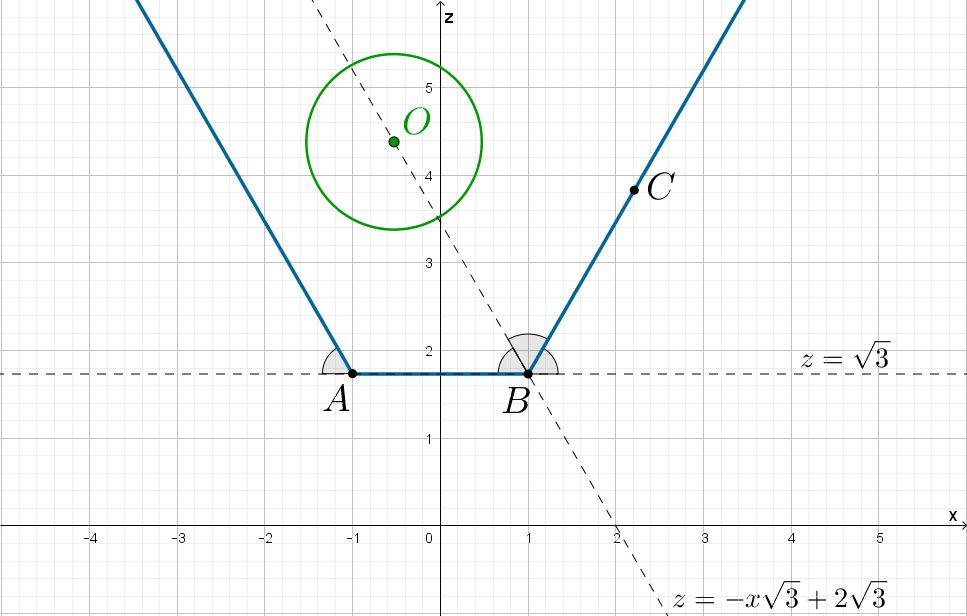
Заметим, что так как правая ветвь корыта задается уравнением то
она наклонена к положительному направлению оси абсцисс под углом
Так
как угловой коэффициент траектории движения центра окружности равен
то она наклонена к положительному направлению оси абсцисс под
углом
Следовательно, прямая, являющаяся траекторией движения
центра окружности, делит
пополам (все отмеченные на рисунке
углы равны по
). Следовательно, если окружность касается правой
ветви корыта — луча
то она касается также и основания корыта
Также заметим, что, находясь в таком положении, окружность не
имеет точек пересечения с левой ветвью корыта. Действительно, для этого
нужно показать, что расстояние между траекторией движения центра и
левой ветвью корыта, которые являются параллельными, больше радиуса
окружности.
Проведем перпендикулярно траектории движения центра окружности.
Получим прямоугольный
с
Следовательно,
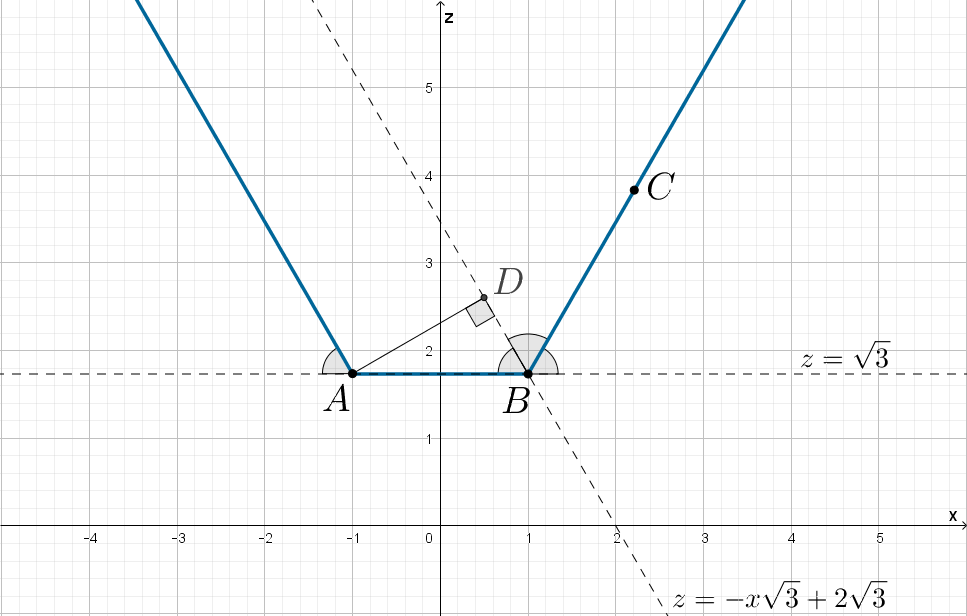
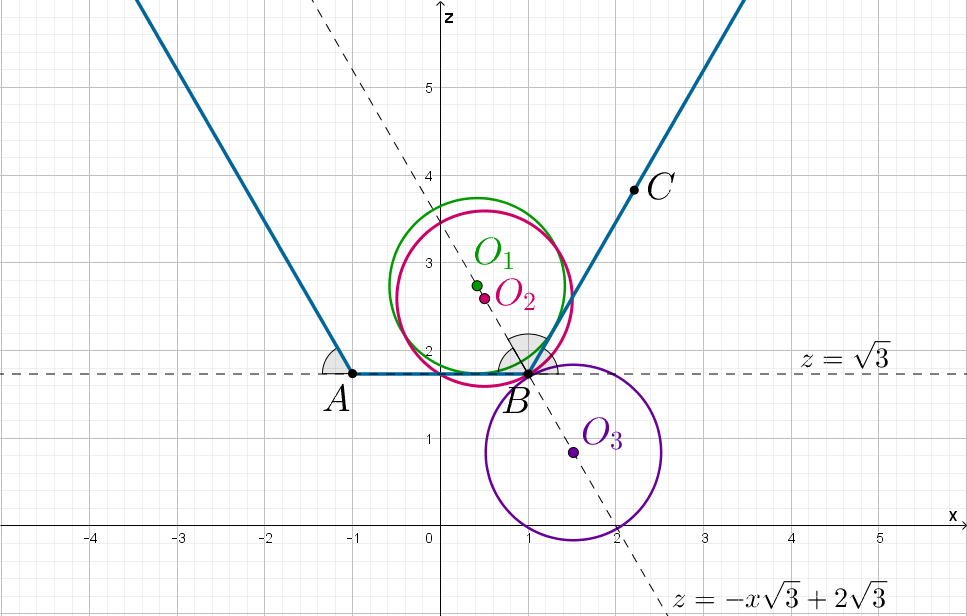
Таким образом, положения, когда окружность имеет с корытом две общие точки, это:
— когда она касается сторон то есть ее центр находится в точке
— когда ее центр находится между точками и
где
и
— положения центра окружности, когда она проходит через точку
Ищем положение точки
Следовательно, ордината точки
равна
Отсюда
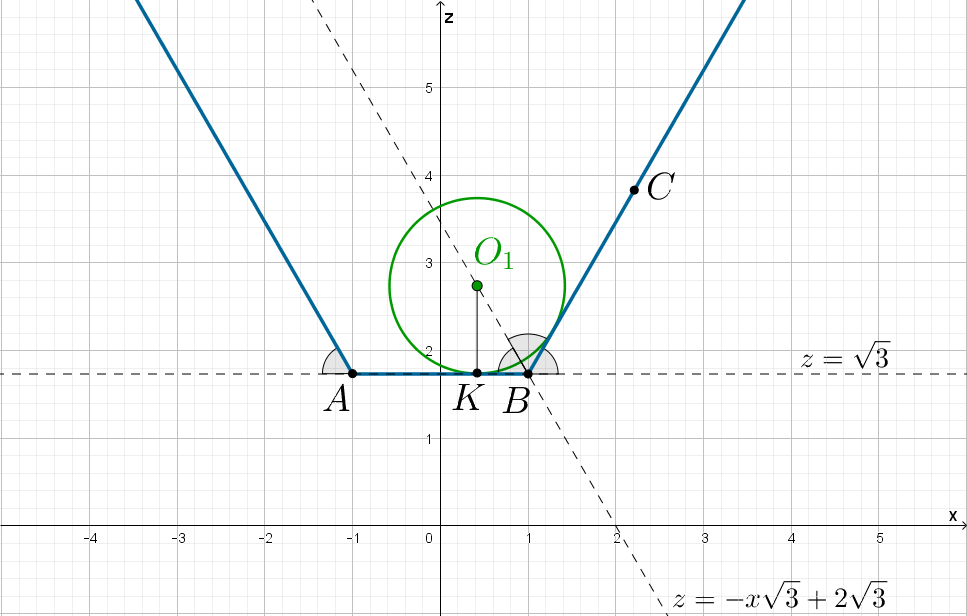
Ищем положение точек и
Координаты точки Так как окружность проходит через эту точку, то
она удовлетворяет уравнению окружности:
Таким образом, ответ:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование | 3 |
| ИЛИ | |
| допущена вычислительная ошибка | |
| Найдено конечное число значений
параметра | 2 |
| Cведено к исследованию графически или аналитически и выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все положительные значения при каждом из которых множеством
решений неравенства
является некоторый луч.
Так как мы рассматриваем данное неравенство только при то знаменатель
представляет собой квадратичный трехчлен от
Заметим, что по теореме Виета
его корнями являются числа
и
так как
Следовательно, неравенство можно переписать в виде:
Если решать данное неравенство методом интервалов, то необходимо отметить
нули числителя и нули знаменателя на вещественной прямой, они образуют
промежутки, на каждом из которых левая часть неравенства принимает значения
одного знака. Далее необходимо найти знак на каждом из таких промежутков.
Тогда решением неравенства будут те промежутки, над которыми стоит знак
«».
Заметим, что коэффициенты при во всех скобках положительны. Тогда если
все три корня различны, то картинка будет выглядеть так:
Видим, что в этом случае решение неравенства будет представлять собой объединение луча и отрезка (вместо отрезка может быть интервал или полуинтервал). Следовательно, этот случай нам не подходит.
Значит, некоторые корни должны совпадать. Мы понимаем, что луч может
получиться только если самая правая точка не будет выколотой, значит, самой
правой должна быть точка При этом она не должна совпадать ни с какой
другой.
Значит, Тогда
так как по условию
Следовательно,
неравенство имеет вид
Получили луч, следовательно, этот случай нам подходит. Таким образом,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получено искомое значение параметра, но допущена одна вычислительная ошибка (описка) | 3 |
| С
помощью верного рассуждения получено
значение параметра (возможно неверное
из-за одной вычислительной ошибки), но
решение недостаточно обосновано
(например, не обосновано наличие ровно
одного значения | 2 |
| Задача сведена к методу интервалов или исследованию графика, но дальнейшие рассуждения неверны или отсутствуют | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых неравенство
имеет единственное решение.
Заметим, что неравенство вида при
не имеет решений, тогда оно
равносильно системе
При этом даже условие излишне, так как из неравенства
вытекает
, откуда
Cледовательно, неравенство
равносильно неравенству
Тогда наше исходное неравенство равносильно системе
Двойное неравенство имеет единственное решение, если
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Необоснованны переходы в исследовании | 3 |
| Верное решение системы неравенств,
но либо есть ошибка, либо решение не
завершено (не составлено равенство,
позволяющее найти значение
параметра | 2 |
| Выполнен переход к системе двух неравенств | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых уравнение
имеет ровно два различных корня.
Уравнение равносильно
Будем рассматривать параметр как переменную. Построим в системе
координат
множество
решений системы. Если некоторая точка
плоскости с координатами
принадлежит этому множеству
то для
исходной задачи это означает, что если параметр
принимает значение
то
будет одним из решений системы. Нас просят найти все такие
значения
параметра
при каждом из которых существует ровно две
точки вида
,
, принадлежащие множеству решений
изображенному на плоскости
Фактически это равносильно тому, что
горизонтальная прямая
имеет две точки пересечения с множеством
Для каждого фиксированного решениям системы будут те точки
пересечения горизонтальной прямой
с графиком
, которые не
лежат на графике
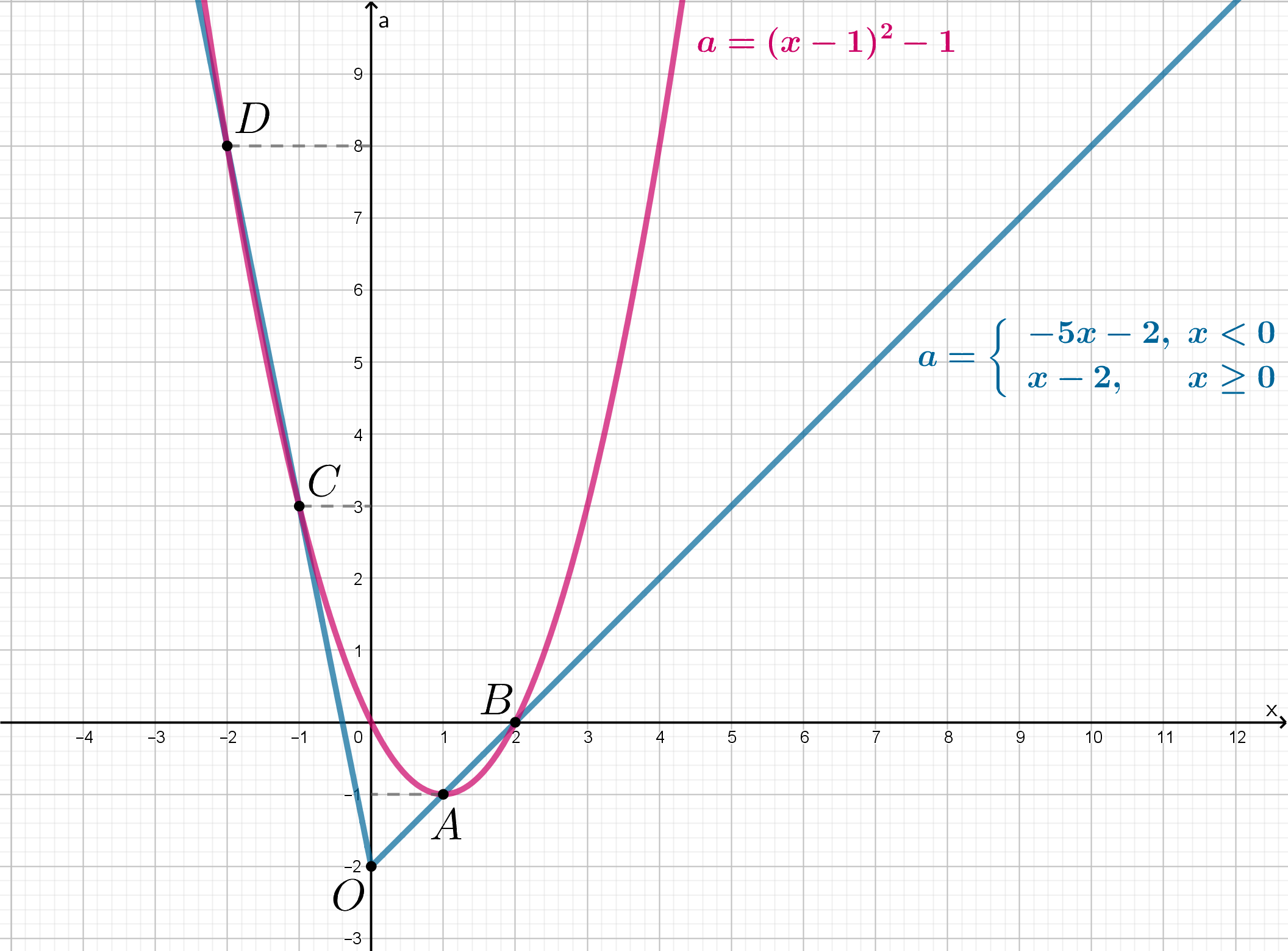
Таким образом, множеством решения системы является множество
состоящее из точек, лежащих на «уголке», с выколотыми точками
Следовательно, при
горизонтальная прямая
имеет с системой две точки пересечения.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых множеством решений
неравенства
является объединение ровно двух непересекающихся промежутков числовой прямой.
По теореме Виета корнями квадратичного многочлена относительно являются
и
. Следовательно, неравенство имеет
вид
Будем решать неравенство в системе координат Тогда первая система
совокупности задает часть плоскости не выше параболы
и не
ниже параболы
Вторая система совокупности задает часть
плоскости не ниже параболы
и не выше параболы
Нам подходят такие горизонтальные прямые , которые пересекают
полученную область по двум непересекающимся промежутками. Это все
горизонтальные прямые выше прямой
прямые
и
а также
все горизонтальные прямые ниже прямой
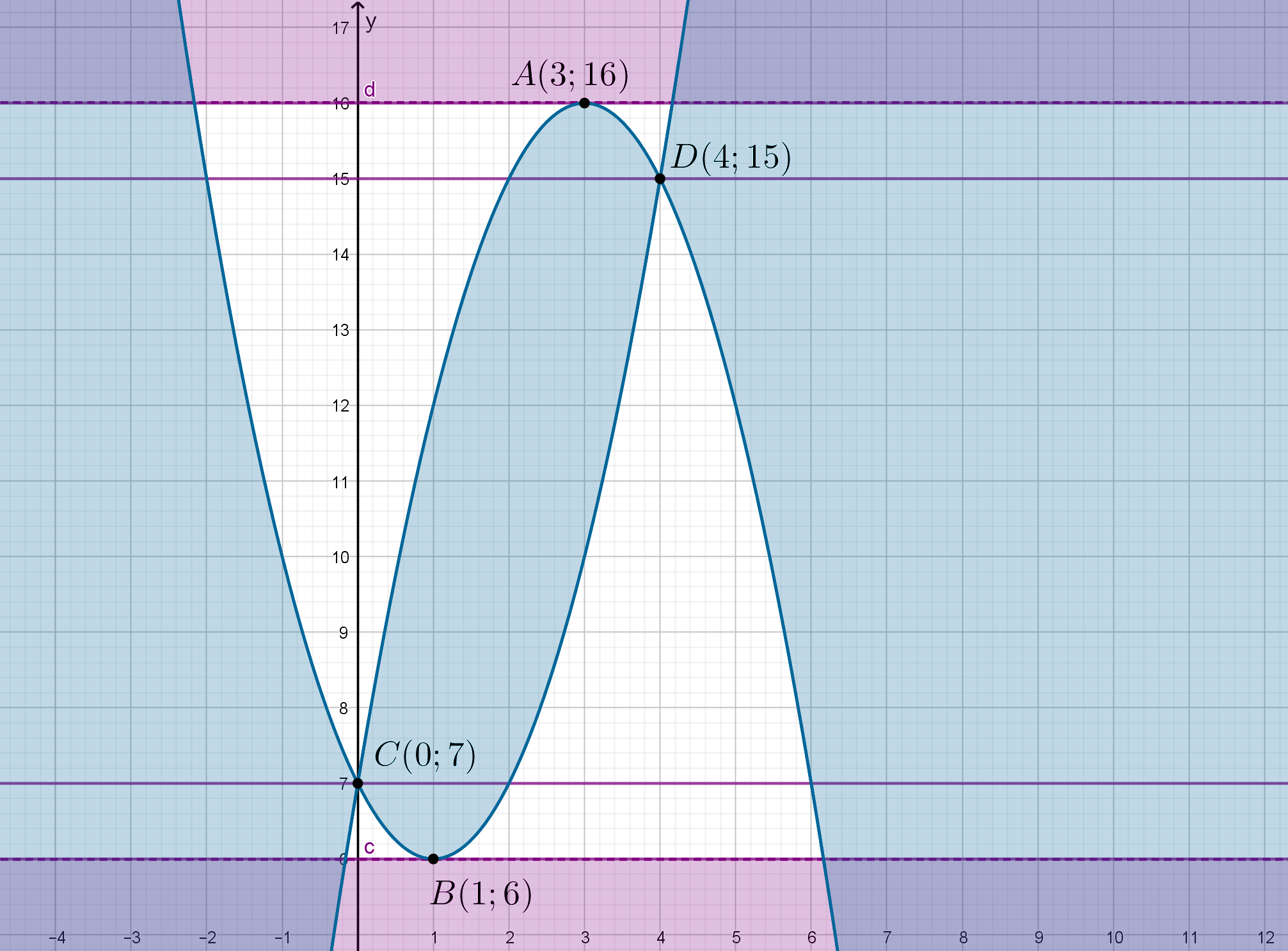
Тогда получаем подходящие значения параметра:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получено
множество значений | 3 |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом в решении представлена правильная графическая интерпретация или правильная аналитика | 2 |
| ИЛИ | |
| в решении верно найдены множества
значений параметра, за исключением
| |
| Верно сведено к исследованию взаимного расположения парабол (аналитически или графически) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых функция
имеет хотя бы одну точку максимума.
Раскроем модуль:
Таким образом, графиком функции является объединение
части левой параболы, соответствующей
и части правой параболы,
соответствующей
Заметим, что эти части «соединяются» в одной точке с
абсциссой
Так как у параболы одна убывающая и одна возрастающая ветвь, то от
каждой параболы можно взять либо только строго монотонную ветвь, либо
часть, состоящую из обеих ветвей, то есть и возрастающей, и убывающей.
Следовательно, график может принимать одну из четырех форм:
![]()
Точка максимума — это такое число в некоторой окрестности которого
точка графика с абсциссой
является самой высокой. Тогда точка максимума
имеется только на последнем рисунке. Последний рисунок задается тем, что
абсцисса
вершины левой параболы строго левее
а абсцисса
вершины правой параболы — строго правее
Тогда получаем
следующее условие на параметр:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку | 3 |
| Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки | 2 |
| Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых уравнение
имеет единственный корень на интервале
Преобразуем исходное уравнение.
В полученном уравнении слева стоит функция — стандартная парабола.
Справа стоит функция
которая задает семейство прямых,
проходящих через точку
Изобразим графики полученных функций на
координатной плоскости, учитывая, что мы ищем корни на интервале
![]()
- При
прямая
не пересекает график функции
на интервале
- При
прямая
пересекает график функции
в точке
- При
прямая
пересекает в двух точках график функции
на интервале
- При
прямая
пересекает график функции
на интервале
ровно в одной точке.
Таким образом, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения
получено множество значений | 3 |
| С помощью верного рассуждения
получены все граничные точки
искомого множества значений | 2 |
| ИЛИ | |
| при верном ходе решения допущена вычислительная ошибка | |
| Верно найдена хотя бы одна
граничная точка искомого множества
значений | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых уравнение
имеет два корня, расстояние между которыми больше 2.
При уравнение является линейным, а линейное уравнение не может иметь
два корня, следовательно, этот случай нам не подходит.
Пусть Тогда уравнение квадратное. Пусть
тогда уравнение имеет два корня
и
Требуется, чтобы
то
есть
По теореме Виета имеем:
Тогда получаем систему:
Следовательно,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения
получены все значения | 3 |
| С помощью верного рассуждения получениы все решения уравнения | 2 |
| Задача верно сведена к исследованию возможного значения корней уравнения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых уравнение
имеет единственное решение.
Пусть ,
, тогда уравнение равносильно
При получаем
, откуда
, откуда
При получаем
Следовательно,
Система имеет решение , если
Следовательно, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения
получено множество значений | 3 |
| С помощью верного рассуждения
получено множество значений | 2 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
| Задача верно сведена к исследованию возможного количества корней уравнения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет единственный корень.
Данное уравнение является квадратным при и линейным при
. Рассмотрим для начала второй случай.
При уравнение примет вид:
то есть
оно имеет единственный корень, что подходит по условию.
При уравнение является квадратным, и в таком случае для
единственности корня необходимо и достаточно того, что дискриминант будет
равен нулю. Запишем его и приравняем нулю:
Итого получаем, что уравнение имеет единственный корень при и
.



