Ошибка.
Попробуйте повторить позже
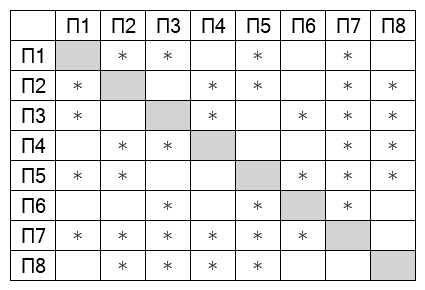
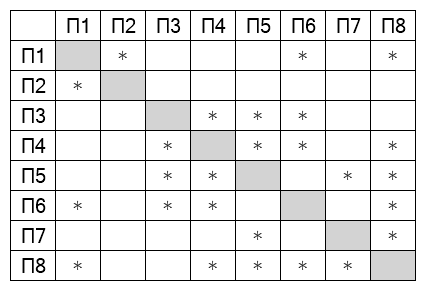
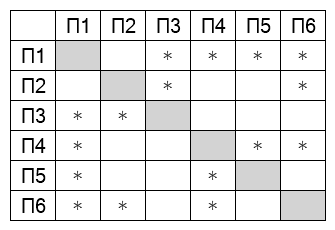
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
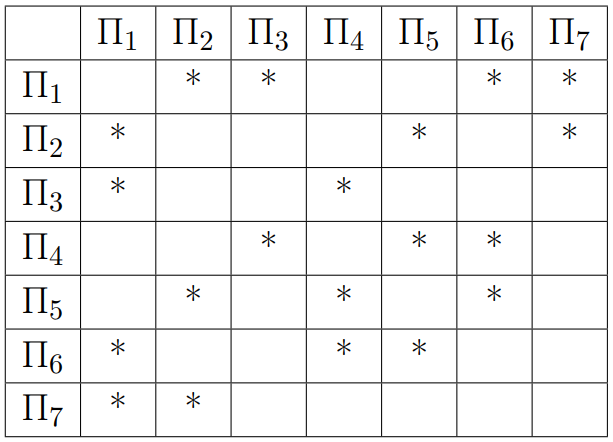
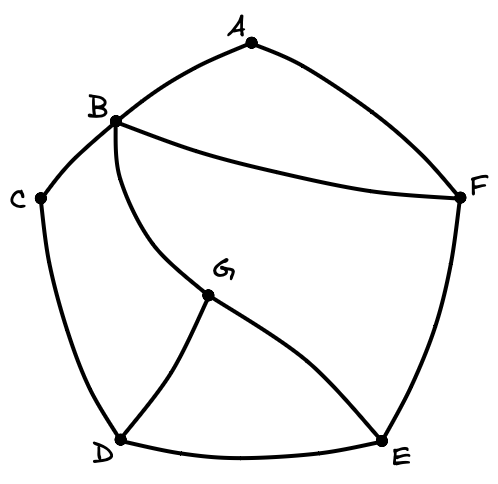
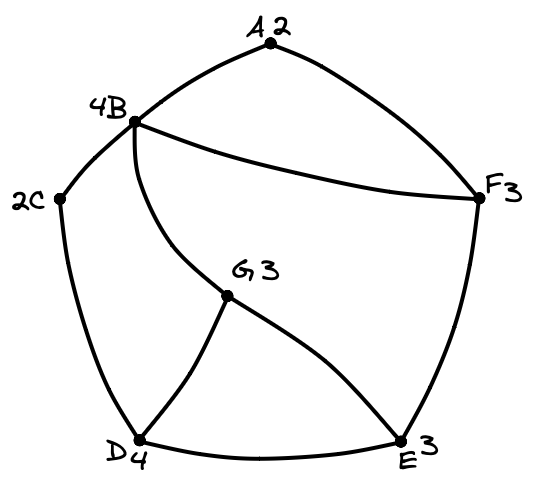
Сначала напишем степени всех вершин: A — , B —
, C —
, D —
, E —
, F —
, G —
.
Заметим, что всего одна вершина имеет степень — это B(П1).
Вершина B связана с четырьмя вершинами, но лишь две из них связаны еще и друг с другом.
Рассмотрим П3, П3 связано с П1 и П4, при этом П4 не связано с П1(B), следовательно, П3(C),
П4(D).
Второй пункт, который также имеет степень и связан с П1(B) — это П7(A).
П7(A) и П1(B) связаны с общим пунктом П2(F).
Пункты П1(B) и П4(D) связаны с пунктом П6(G).
Последний неопознанный пункт П5(E).
Тогда ответ: BFCDEGA
Ошибка.
Попробуйте повторить позже
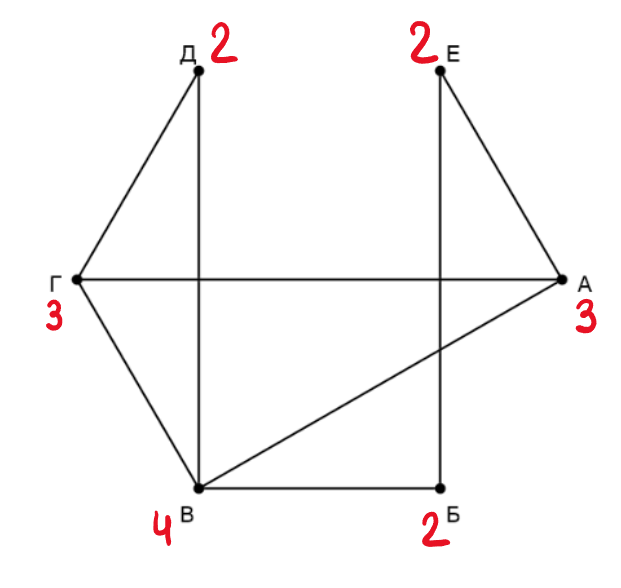
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.
Сначала напишем степени всех вершин: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
.
Заметим, что только одна вершина имеет степень
— это
(
). Ее связывают вершины со степенью
, и остается
лишь одна вершина со степенью
— это
(
). Также заметим, что только одна вершина имеет степень
— это
(
). Две из трех вершин со степенью
связаны друг с другом, значит, оставшаяся —
в пункте
. В вершину
не приходит только
, значит,
—
. Оставшаяся вершина со степенью
— это
, т.е.
.
Одна из вершин со степенью
приходит в
, а вторая — нет. Та, которая приходит,
—
, а
—
.
Получаем ответ: .
Ошибка.
Попробуйте повторить позже
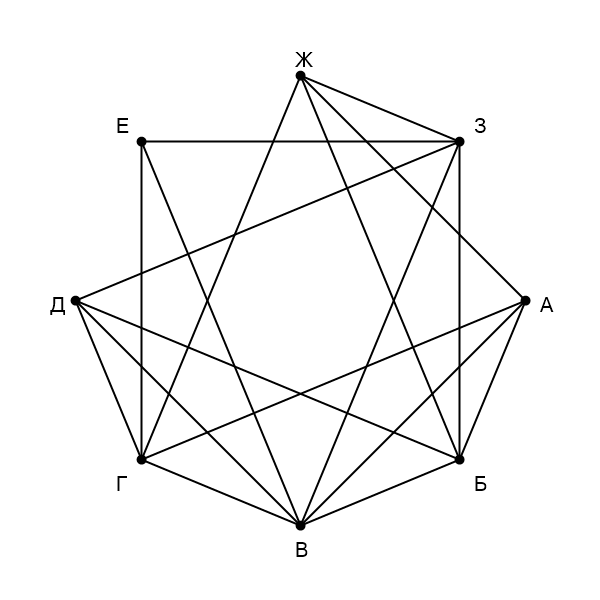
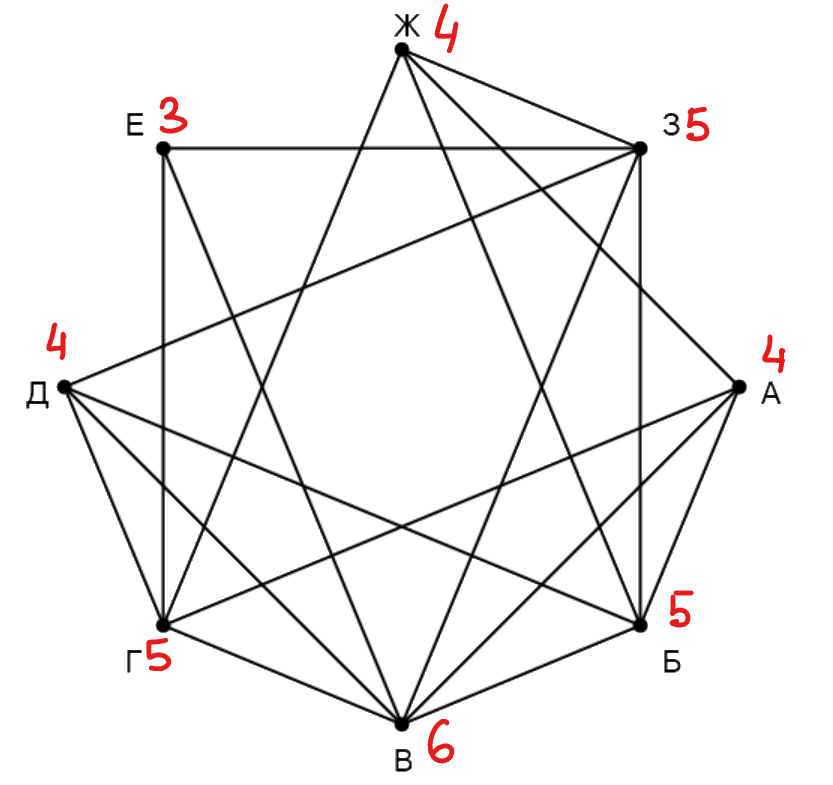
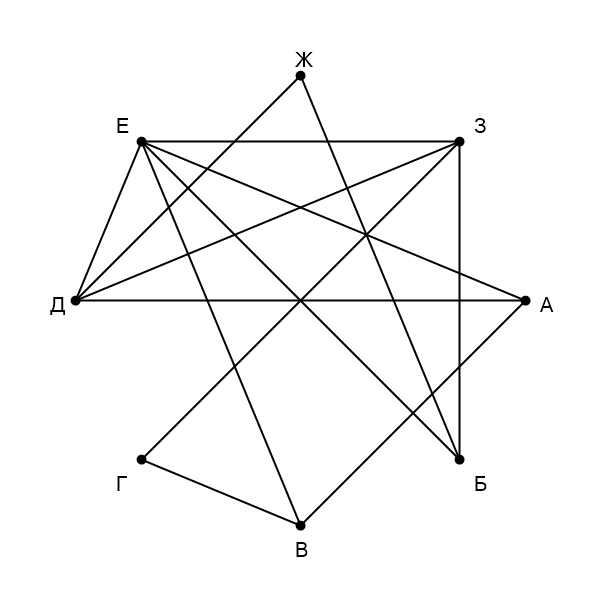
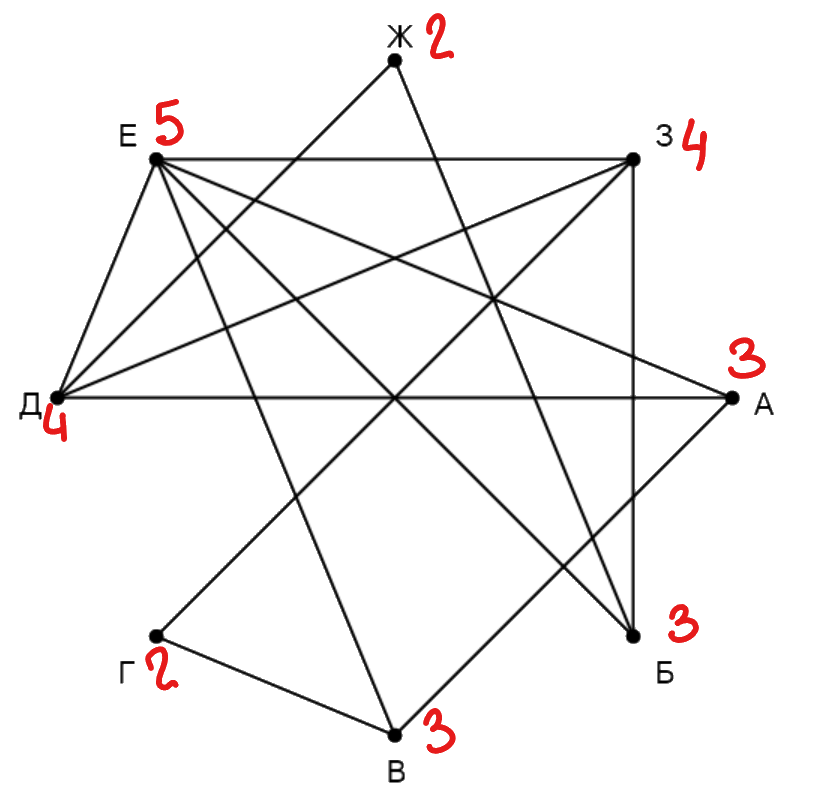
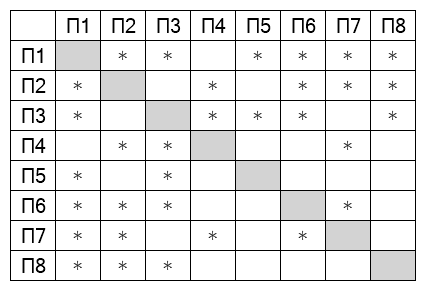
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.

Сначала напишем степени всех вершин: А - , Б -
, В -
, Г -
, Д -
, Е -
, Ж -
, З -
. Вершины степени
(Г и В) связаны одной вершиной степени
- А, тогда А - П
, и одной вершиной степени
- Ж, тогда Ж - П
.
Помимо этого Ж имеет общую дорогу с населённым пунктом Б, значит, Б - П
. У нас осталась одна вершина
степени
- З => З - П
, одна вершина степени
- Е => Е - П
, и одна вершина степени
- Д => Д -
П
. Населённый пункт З имеет дороги с Д (П
) и Г, значит, Г - П
, тогда оставшаяся вершина В - П
.
Получаем ответ: ГВДБЕЗЖА
Ошибка.
Попробуйте повторить позже
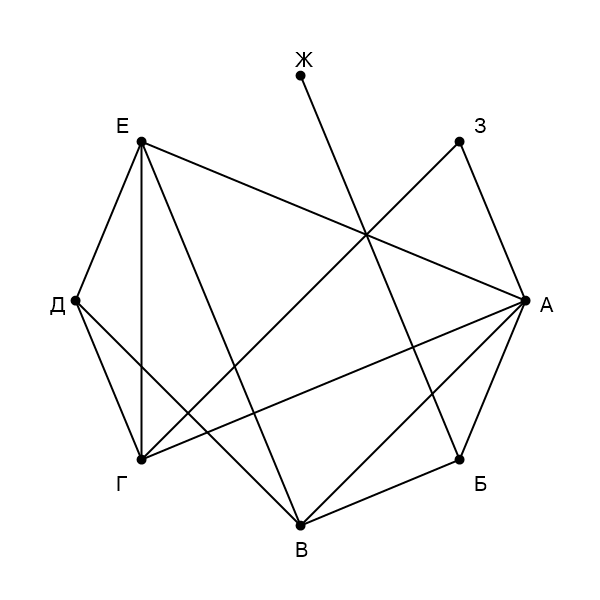
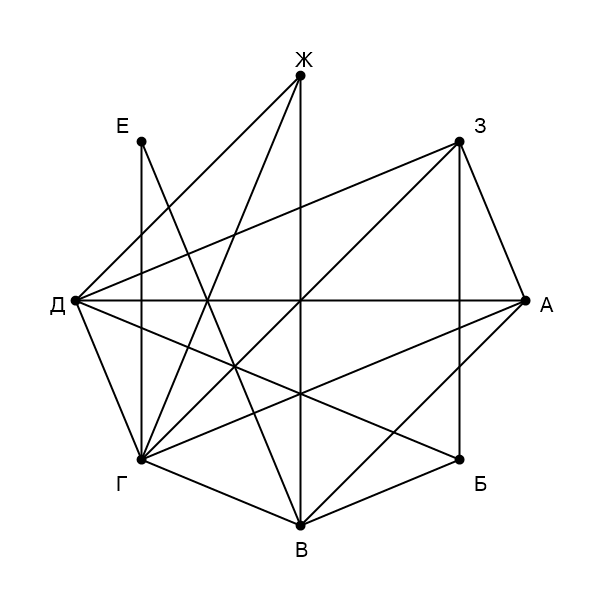
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.

Сначала напишем степени всех вершин: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
.
Заметим, что только одна вершина имеет степень
— это
, тогда
—
. Вершина
имеет степень
, она одна
из вершин, имеющих такую степень и не связанных с вершинами степени
, значит,
—
. Она связана с
единственной вершиной степени
—
, тогда
—
, и единственной вершиной степени
—
, тогда
—
. У
нас остался один пункт со степенью
—
, ему соответствует
, и пункт со степенью
—
, ему соответствует
. Вершины
и
связывают
(
) и
, тогда
—
. По остаточному принципу
—
.
Получаем ответ:
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.
Подпишем все степени вершин (количество ребер, выходящих из вершины) в таблице и на графе: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
. У нас три вершины с уникальными степенями, можем их сопоставить:
—
,
—
,
—
. Вершина
связана только с
, можем найти
:
—
.
связана с двумя вершинами, одна из которых
известна, значит,
—
. Осталась одна неизвестная вершина степени
, можем найти её в таблице:
—
. Из двух оставшихся вершин одна связана с
, другая нет, можем найти обе:
—
,
—
.
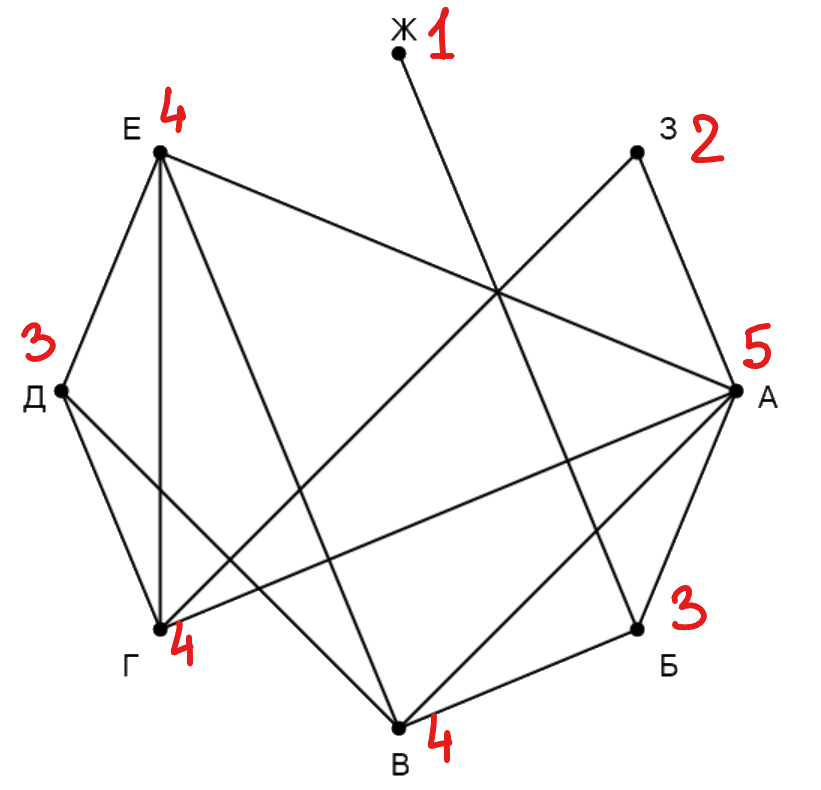
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.
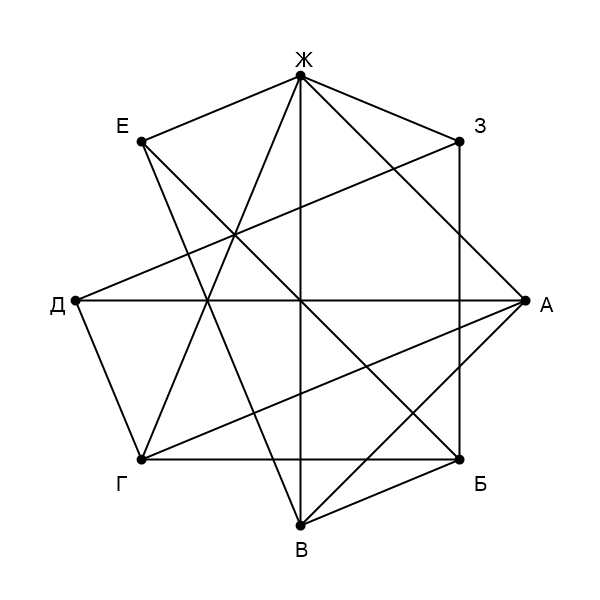
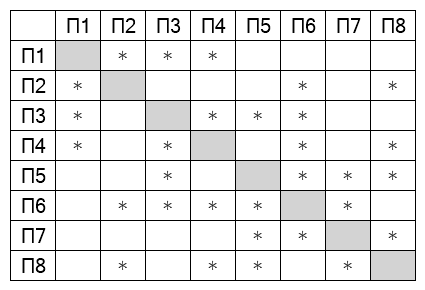
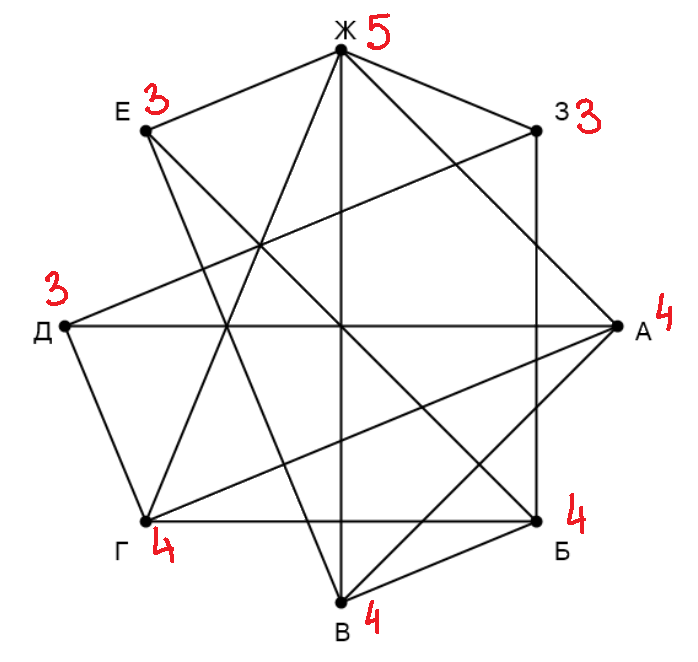
Сначала напишем степени всех вершин: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
.
Заметим, что только одна вершина имеет степень
— это
, тогда
— П
. Пункты
и
не связаны с
,
тогда
—
(степень вершины
), а
—
(степень вершины
).
и
связаны с
и
, значит,
—
,
—
. Вершины
и
связывает
, тогда
—
. Остались вершины
и
, они имеют разное
количество дорог, поэтому можем найти соответствующие пункты в таблице. Таким образом,
—
,
—
.
Получаем ответ:
Ошибка.
Попробуйте повторить позже
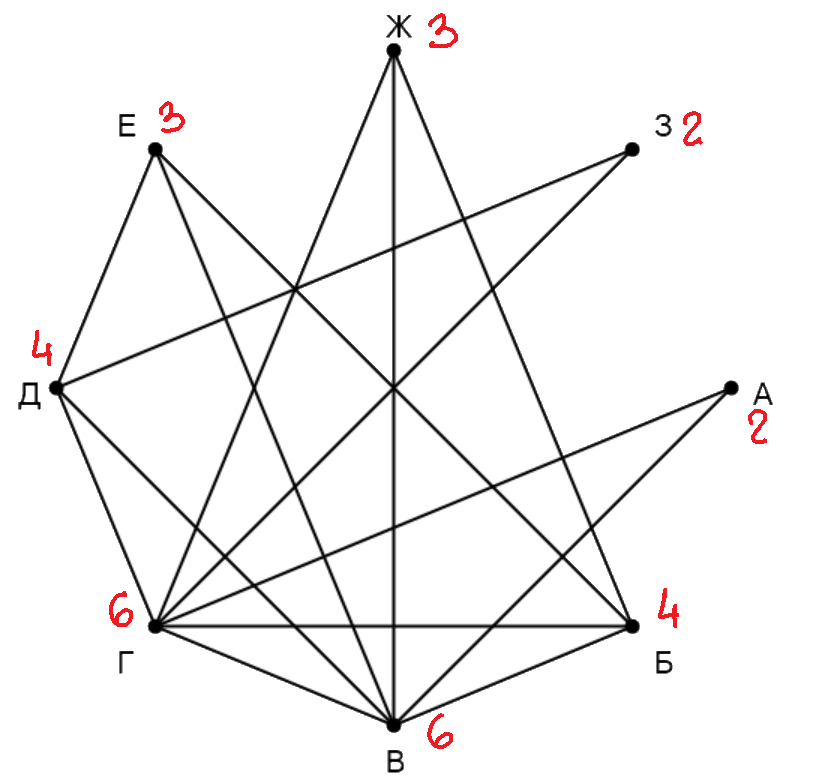
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Е в пункт Л.
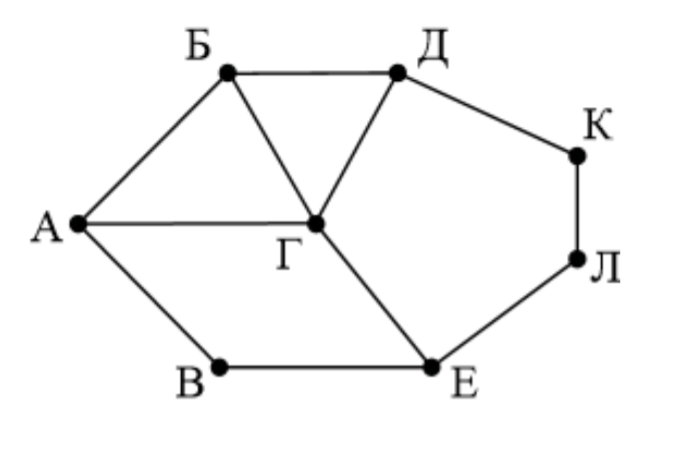
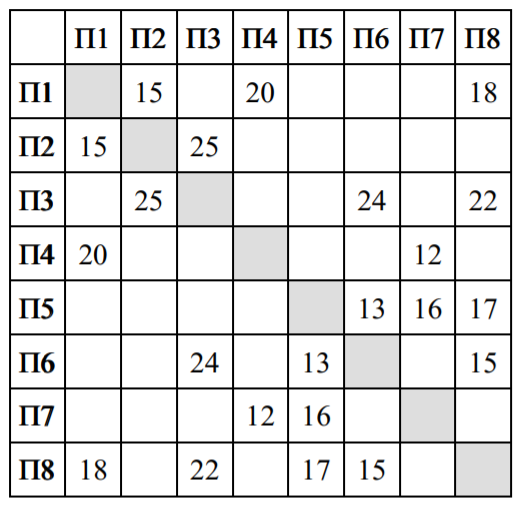
Сначала напишем степени всех вершин: А - , Б -
, В -
, Г -
, Д -
, Е -
, К -
, Л -
. Можем заметить,
что только одна вершина имеет степень
- это Г, тогда Г - П
. Вершина Г связана с А и Е, которые в свою очередь
связаны с В, тогда среди вершин степени
определим ту, что имеет общие дороги только с вершинами степени
,
следовательно, В - П
. Аналогично, лишь одна вершина имеет степень
и связана с двумя другими, имеющими ту же
степень, получим, что Б - П
. В и Б связывает А, тогда А - П
. Также В связана с Е, значит, Е - П
. Из вершин
степени
осталась только Д, ей соответствует П
. К имеет общую дорогу с Д, тогда К - П
, а Л - П
.
Найдём в таблице длину пути из Е (П) в Л (Л
) и запишем полученное значение в ответ.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа. В таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
и т. д.
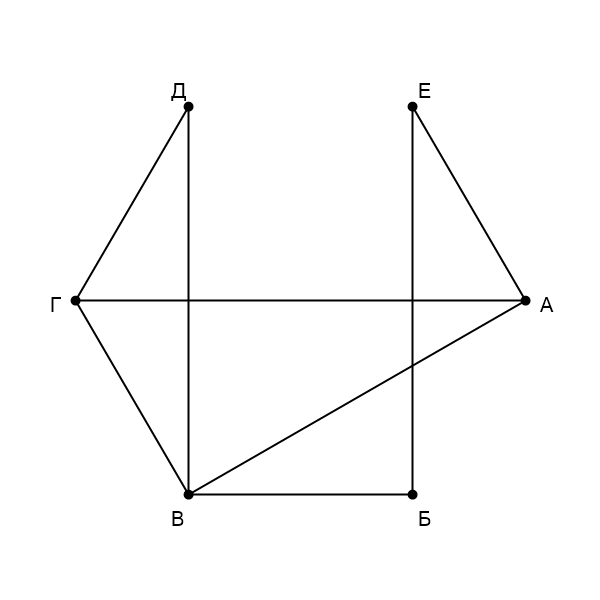
Распишем степени вершин. Видим, что единственная вершина степени это
—
. Вершина
не связана только
с одной вершиной —
, соответственно
—
. Вершина
связана с
и
, соответственно
и
. По
оставшимся степеням вершин
—
,
—
.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
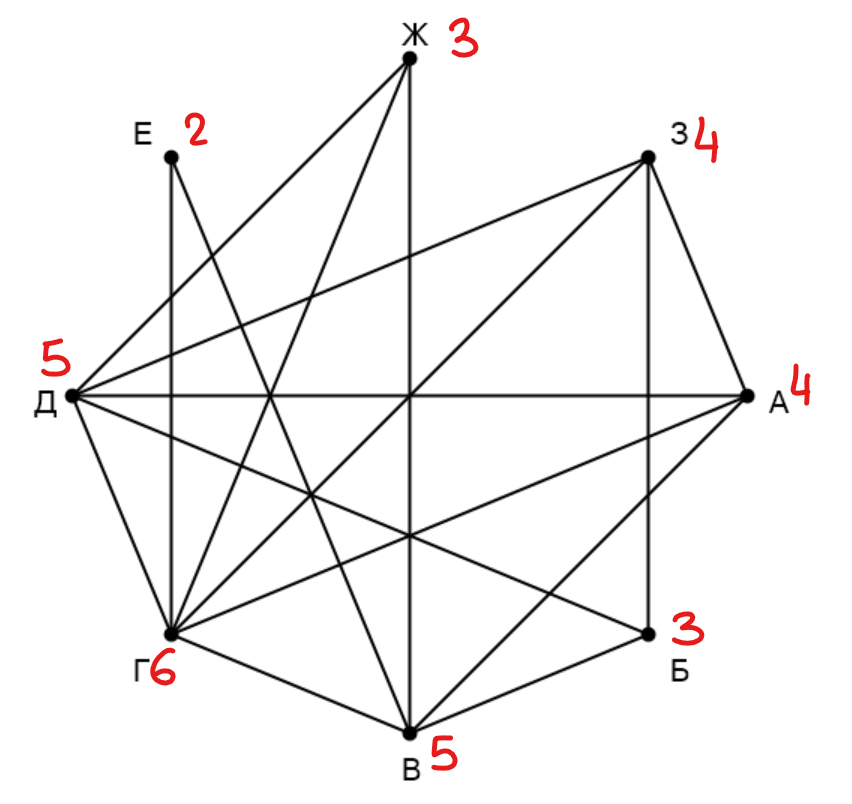
Подпишем степени вершин. Е — единственная вершина со степенью , ей соответствует П5. Она связана с вершиной Г
со степенью
и с вершиной В со степенью
. Им соответствуют П1 и П3 соответственно. Оставшаяся вершина Д со
степенью
соответствует П2. Вершина Г не связана с вершиной Б. Значит, вершине Б соответствует П4.
Вершина Б связана с вершиной З. Ей соответствует П7. Оставшимся вершинам А и Ж соответствуют П6 и П8
соответственно.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответ. П1, затем букву, соответ. П2, и т. д.
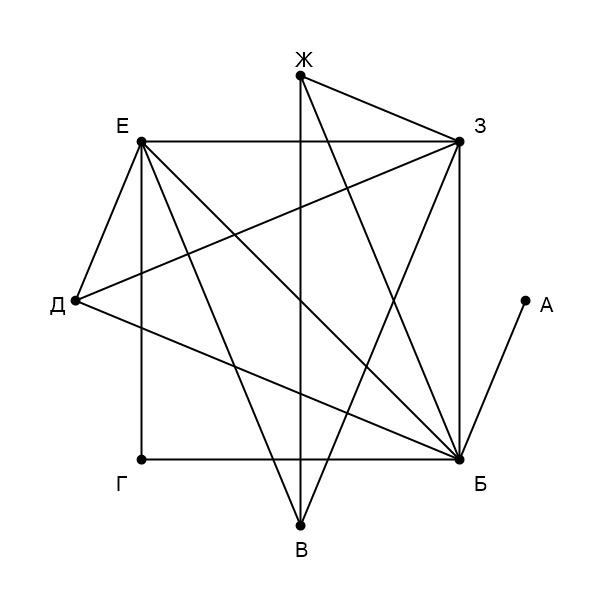

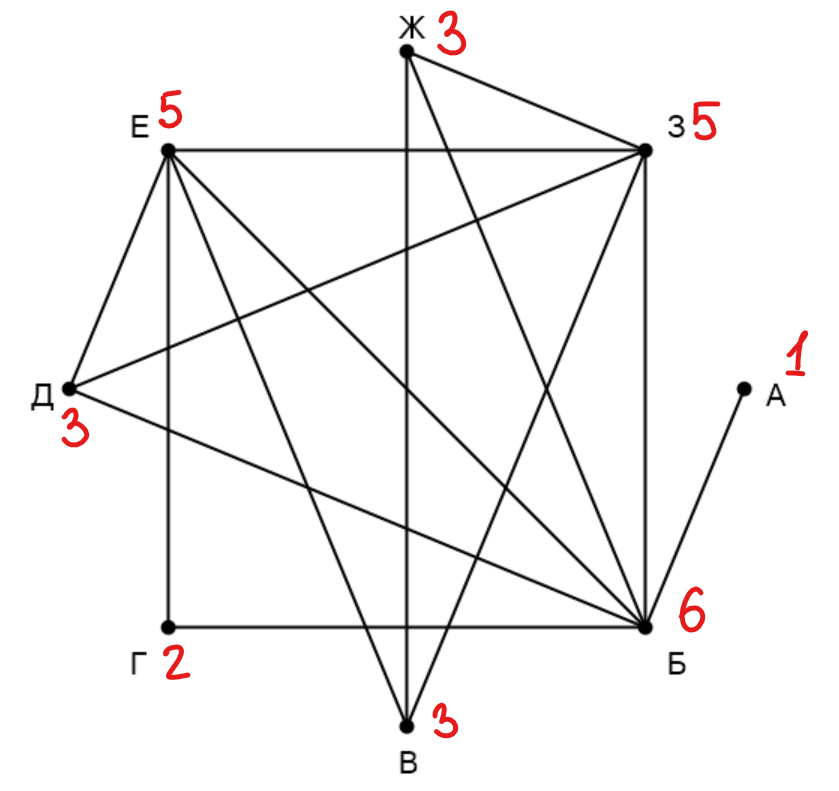
Подпишем все степени вершин (количество ребер, выходящих из данной вершины) на графе и в таблице: А - 1, Б - 6, В - 3, Г - 2, Д - 3, Е - 5, Ж - 3, З - 5, П1 - 3, П2 - 5, П3 - 2, П4 - 1, П5 - 6, П6 - 3, П7 - 3, П8 - 5. У нас есть 3 вершины с уникальными степеням, сопоставим их в таблице и на графе: П3 - Г, П4 - А, П5 - Б. Вершина Г связана с двумя вершинами, одна из которых известна, можем найти вторую: П2 - Е. Осталась одна неизвестная вершина степени 5, найдём её в таблице: П8 - З. Мы знаем все связи вершины Д в таблице, можем определить вершину Д: П6 - Д. Из двух оставшихся неизвестных одна связана с Е, другая нет, можем определить обе: П1 - В, П7 - Ж.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Запишите в ответ значение выражения (А
Б
В
Г
Д
Е
З
Ж), где вместо каждого буквенного обозначения пункта нужно подставить
соответстующий номер пункта в таблице, например если П1 = А, то в выражение вместо А нужно подставить
1.
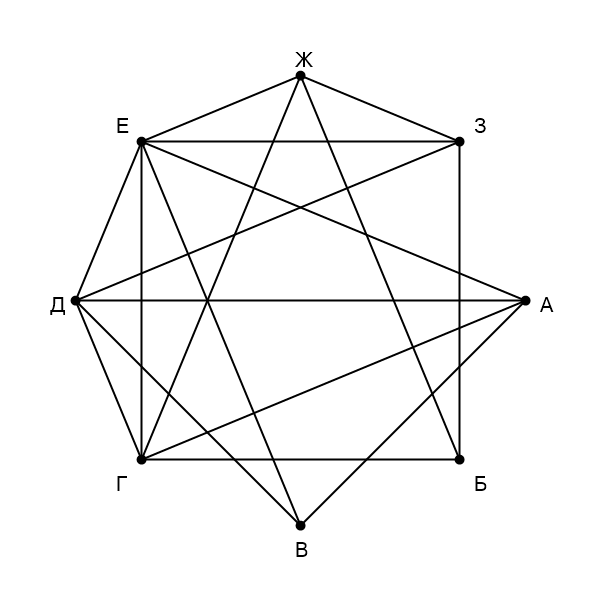
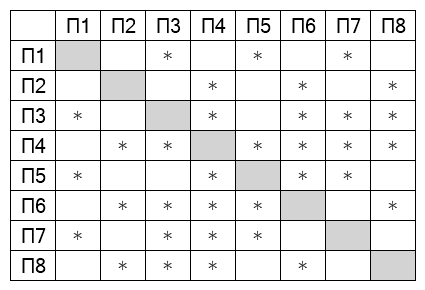
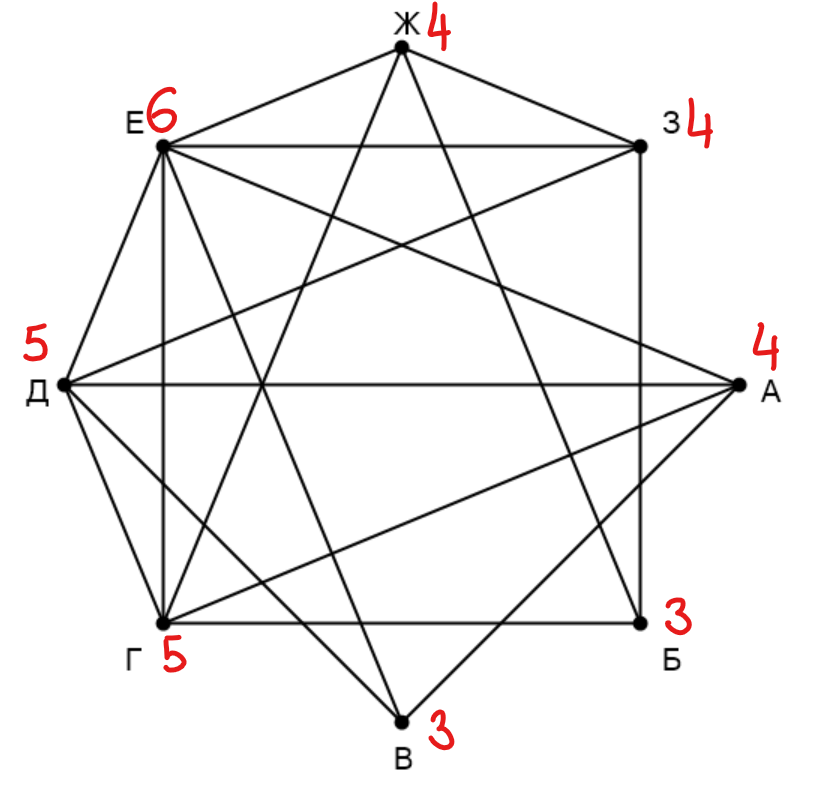
Подпишем на графе и в таблице степени вершин (количество ребер, выходящих из них): А - 4, Б - 3, В - 3, Г - 5, Д - 5, Е - 6, Ж - 4, З - 4, П1 - 3, П2 - 3, П3 - 5, П4 - 6, П5 - 4, П6 - 5, П7 - 4, П8 - 4. У нас есть одна вершина с уникальной степенью: П4 - Е. Кроме того, только вершина Б не имеет связи с Е, значит, П1 - Б. Вершина Б связана с двумя вершинами степени 4 и одной вершиной степени 5, вершину степени 5 можем найти: П3 - Г. Осталась одна неизвестная вершина степени 3, можем найти её: П2 - В. Осталась одна неизвестная вершина степени 5, её тоже можно определить: П6 - Д. Мы знаем все связи вершины А, номера этих вершин известны, можем определить по таблице, что П8 - А. Из оставшихся вершин одна связана с Г, другая нет, можем найти обе: П7 - Ж, П5 - З.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
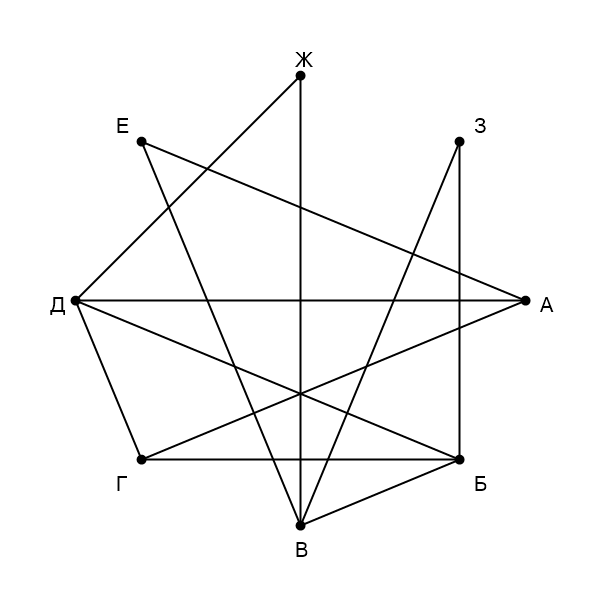
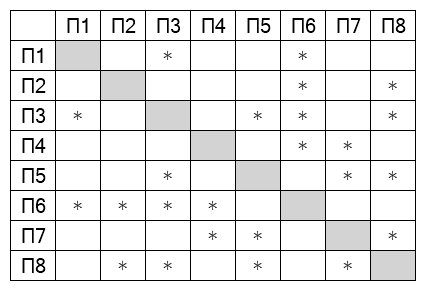
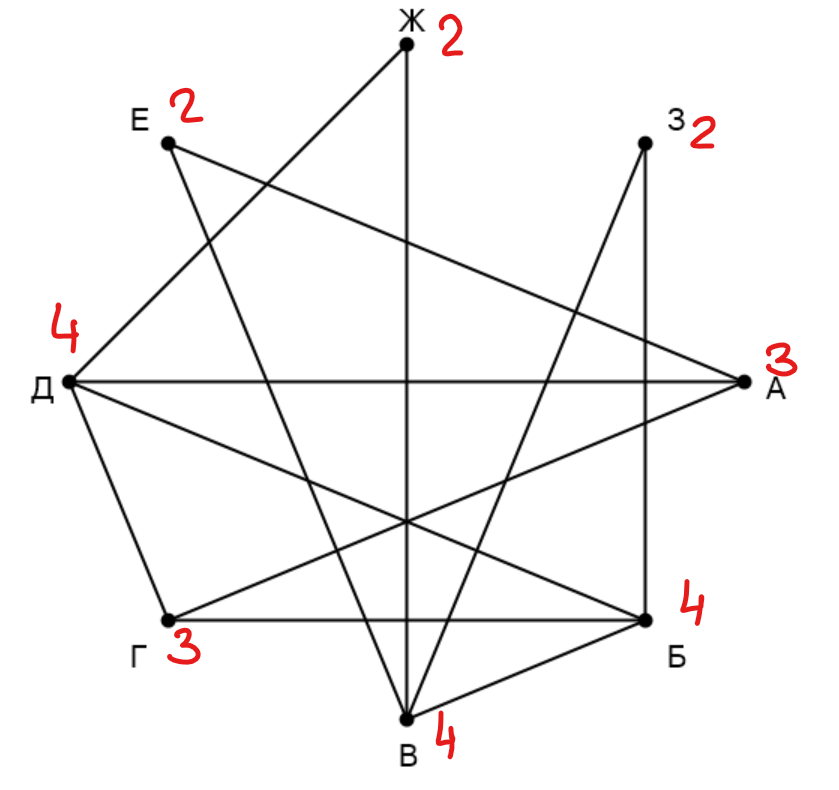
Подпишем все степени (количество ребер, выходящих из вершины) вершин на графе и в таблице: А - 3, Б - 4, В - 4, Г - 3, Д - 4, Е - 2, Ж - 2, З - 2, П1 - 2, П2 - 2, П3 - 4, П4 - 2, П5 - 3, П6 - 4, П7 - 3, П8 - 4. У нас есть две вершины степени 3: Г связана с вершинами со степенями 4, 4, 3, А связана с вершинами со степенями 2, 4, 3. Можем найти по этим связям в таблице обе: П5 - Г, П7 - А. Так как А связана с вершинами разных степеней, все они определяются однозначно: П4 - Е, П8 - Д. Е связана с двумя вершинами, одну из которых мы уже знаем, можем найти вторую: П6 - В. Осталась одна неизвестная вершина степени 4: П3 - Б. Две оставшиеся вершина по связям определяются однозначно: П1 - З, П2 - Ж.
Ошибка.
Попробуйте повторить позже
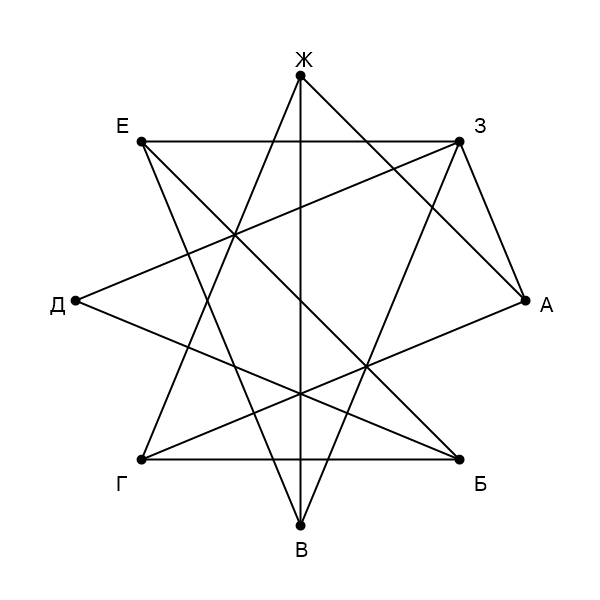
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
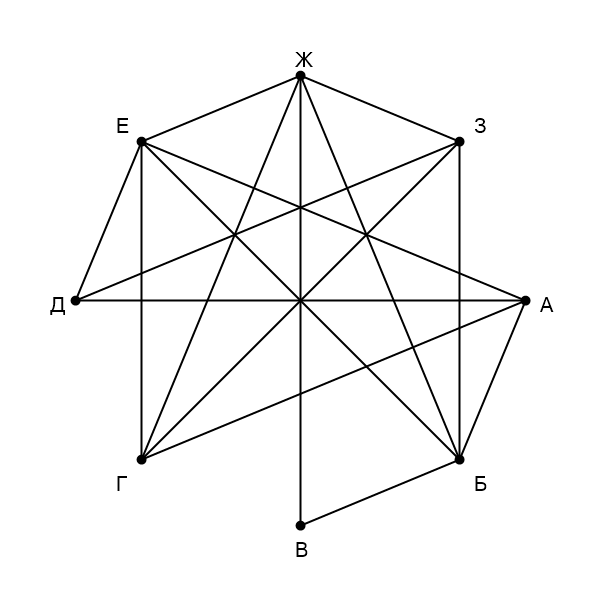

Сначала напишем степени всех вершин: А - , Б -
, В -
, Г -
, Д -
, Е -
, Ж -
, З -
. Заметим, что
только одна вершина имеет степень
- это В, тогда В - П
. Также лишь одна вершина имееь степень
- это Д,
тогда Д - П
. Вершина Д (П
) связана с двумя вершинами, степени которых равны
, и с одной (Е),
степень которой равна
. Тогда Е - П
. Е (П
) и Д (П
) имеют общую вершину А, значит, А - П
.
Вершины А (П
) и В (П
) связывает Б, тогда Б - П
. Пункт В (П
) имеет общие дороги с Б (П
) и
Ж, тогда Ж - П
. Определим, чему соответствуют оставшиеся вершины. Заметим, что Б (П
) связана с
З, тогда З - П
, так как только данный пункт пока не имеет буквенного обозначения. Значит, Г - П
.
Получаем ответ: ЕВЖАЗГБД
Ошибка.
Попробуйте повторить позже
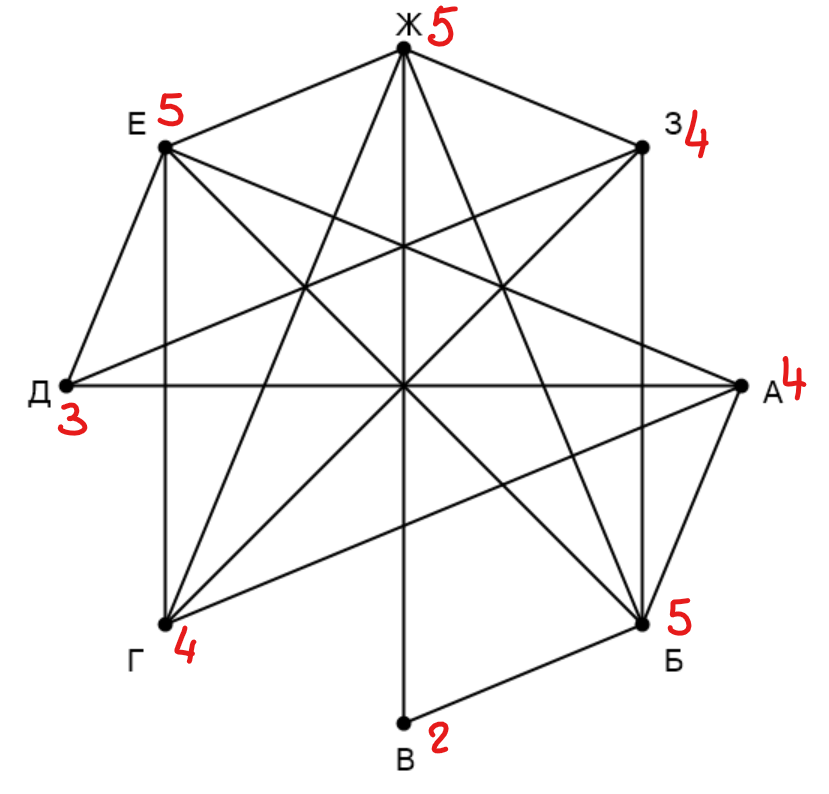
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.

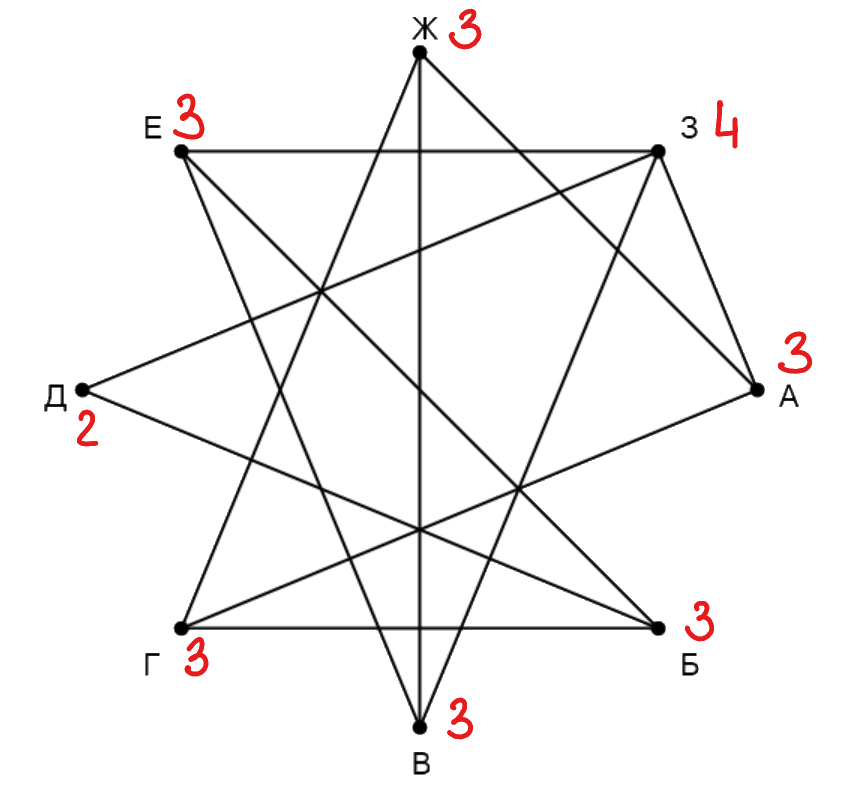
Сначала напишем степени всех вершин: А - , Б -
, В -
, Г -
, Д -
, Е -
, Ж -
, З -
.
Заметим, что только одна вершина имеет степень
- это Д, тогда Д - П
. Также лишь одна вершина имееь
степень
- это З, тогда З - П
. Вершина Д связана с З (П
) и Б, значит, Б - это П
. Пункты Б и З
связавает Е, тогда Е - П
. Е (П
) связана с З (П
), Б (П
) и В, по таблице смежности определяем, что В
- это П
. Вершина В (П
) связана с Е (П
), З (П
) и Ж, методом исключения, используя таблицу,
определяем, что Ж - это П
. Пункты Ж (П
) и З (П
) связывают В (П
) и А, так как В нам исвестна,
то по остаточному принципу А - это П
. У нас осталось одна вершина - Г, которая соответствует П
.
Получаем ответ: ВАДГЖЕБЗ
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания, указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.
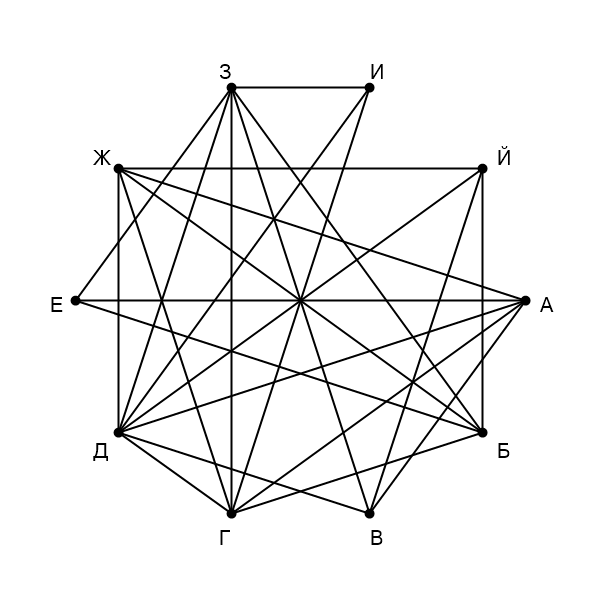

![]()
Сначала напишем степени всех вершин: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
,
—
. Можем заметить, что только одна вершина имеет степень
— это
,
тогда
—
. Вершина
связана со всеми вершинами, кроме
и
, значит,
— это
(так как
имеет степень
, как и
), а
— это
(так как
имеет степень
, как и
). Вершина
(
) связана с
,
и
, так как
мы уже знаем, то не составит труда определить
и
,
ведь у них разные степени, получаем, что
— это
, а
—
. Вершина
связана с
, имеющей
степень
, значит
— это
, тогда вершина
(которая также имеет степень
, но не связана с
) —
это
.
связана с
и
, из них мы не знаем, какому пункту соответствует
, но знаем
другие, тогда свободный пункт, связанный с
—
, значит, вершине
соответствует
. Заметим,
что теперь у нас остались два пункта, и оба с разными степенями, значит, можем определить вершины!
имеет степень
, как и свободная вершина
, а
имеет степень
, как и свободная вершина
.
Получаем ответ:
Ошибка.
Попробуйте повторить позже
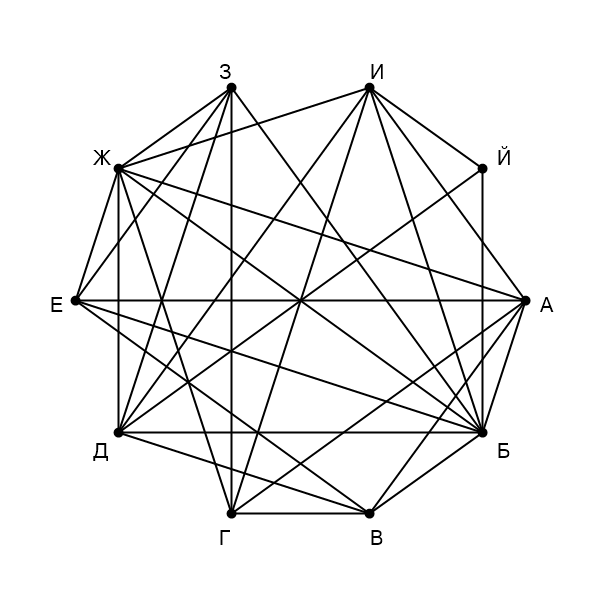
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П10: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.

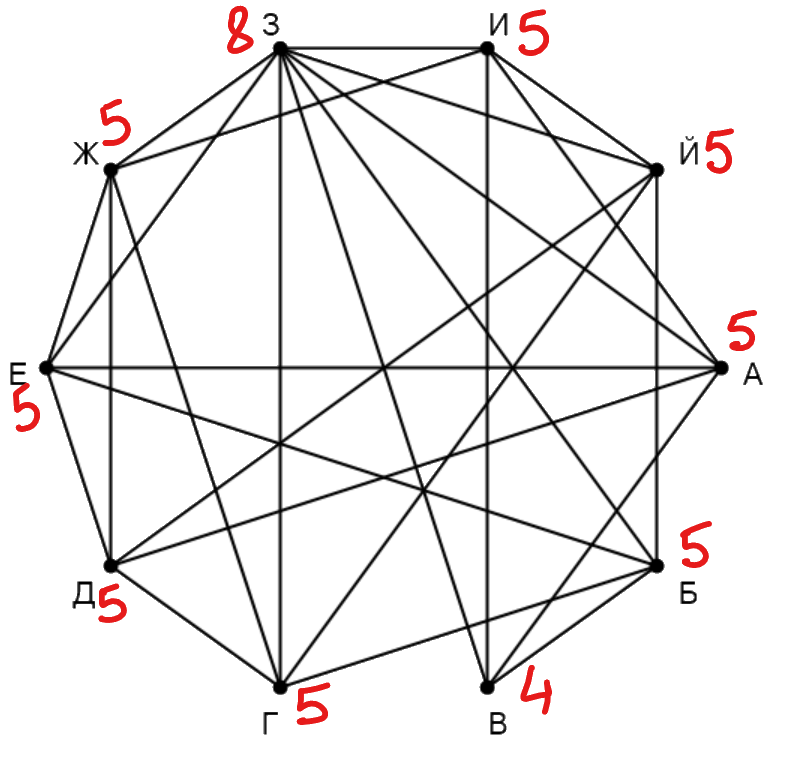
Подпишем степень (количество ребер, выходящих из нее) вершин на графе и в таблице. Получаем на графе: А - 5, Б - 5, В - 4, Г - 5, Д - 5, Е - 5, Ж - 5, 3 - 8, И - 5, Й - 5. В таблице: П1 - 5, П2 - 5, П3 - 5, П4 - 5, П5 - 4, П6 - 5, П7 - 8, П9 - 5, П10 - 5. У нас есть 2 две вершины с уникальными степенями, З и В, подпишем их в таблице: П5 - В, П7 - З. Только одна вершина не связана с З - это Д - найдём её в таблице: П6 - Д. Вершина В связана с тремя вершинами степени 5, и только одна из них связана с Д, найдём её в таблице: П9 - А. Из связей вершины В вершина А связана с И, но не связана с Б. Можем найти Б и И: П2 - И, П3 - Б. Вершина Б из оставшихся неизвестных связана со всеми, кроме Ж, можем найти Ж: П1 - Ж. Вершина Ж из оставшихся неизвестных не связана только с Й, находим: П4 - Й. Вершина Г связана с Й, а Е не связана, ищем в таблице: П8 - Г, П10 - Е.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П10: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.

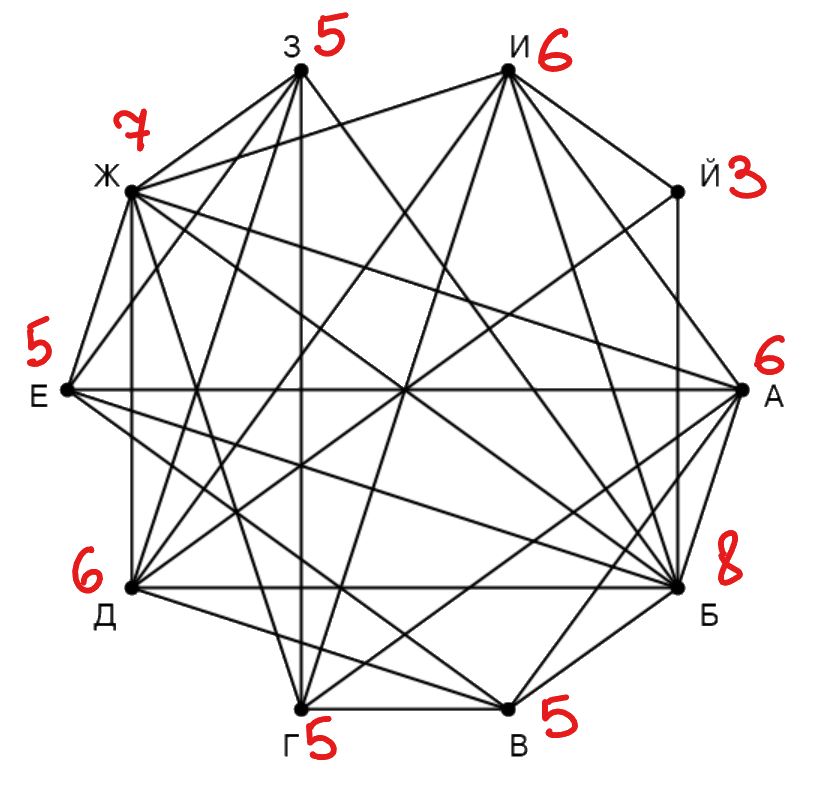
Подпишем у каждой вершины ее степень (количество ребер, выходящих из нее): А - 6, Б - 8, В - 5, Г - 5, Д - 6, Е - 5, Ж - 7, З - 5, И - 6, Й - 3. У нас есть сразу 3 вершины с уникальными степенями, Б, Й, Ж, найдем их в таблице и получаем: П1 - Б, П2 - Й, П10 - Ж. Г - единственная вершина, не связанная с Б, в таблице это П3, Г - П3. А - единственная вершина степени 6, не связанная с Й, находим в таблице: А - П9. В - единственная вершина степени 5, не связанная с Ж, найдем в таблице: В - П5. Осталось две неизвестных вершины степени 6, одна из которых связана с Г, можем найти обе. Связанная с Г - это П8 - И, не связанная - П6 - Д. Из двух оставшихся вершин одна связана с Д, другая нет. Связанная с Д - это П7 - З, не связанная - П4 - Е.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
, и т. д.
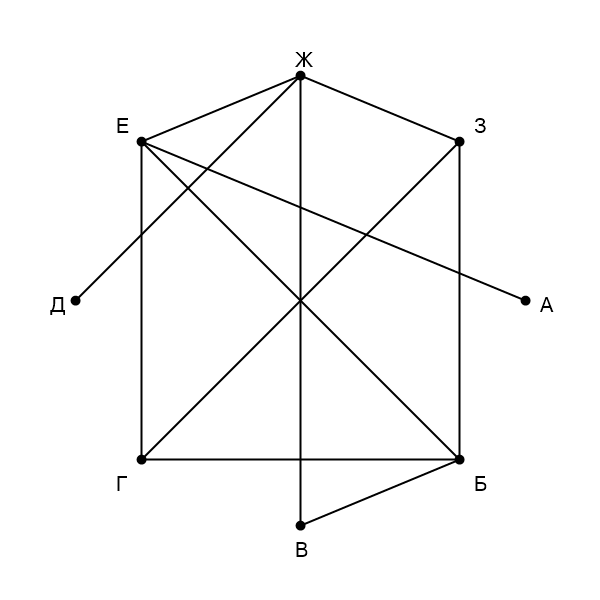

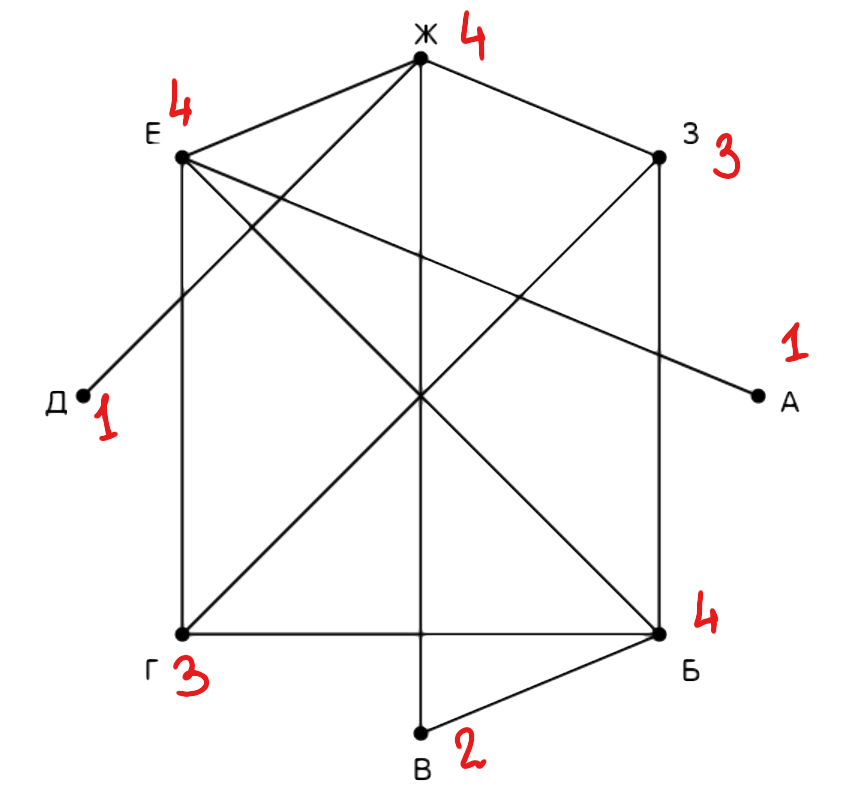
Подпишем около каждой вершины ее степень (количество ребер, выходящих из нее). Получается: —
,
—
,
—
,
—
,
—
,
—
,
—
,
—
. У нас есть вершина с уникальной степень —
— найдём в
таблице вершину степени
—
, получаем:
—
. Из
выходит два ребра, оба степени
, у нас
всего
вершины степени
, две из которых связаны с
, значит, мы можем определить не связанную
— вершина
. Ищем в таблице вершину степени
, не связанную с
, —
, значит,
—
.
связана с вершиной степени
—
, значит, находим в таблице вершину степени
, связанную с
, —
,
значит,
—
. У нас осталась еще одна вершина степени
—
, находим в таблице неизвестную
вершину степени
—
, значит
—
.
связана только с
, значит, единственная связь
в
таблице —
— это
. Единственная неизвестная вершина степени
— это
, находим в таблице
неизвестную вершину степени
—
, значит
—
. У нас осталась две вершины степени
, одна из
которых связана с
, другая с
. Получается,
, связанная с
, — это
, и остается, что
-
.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П10: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
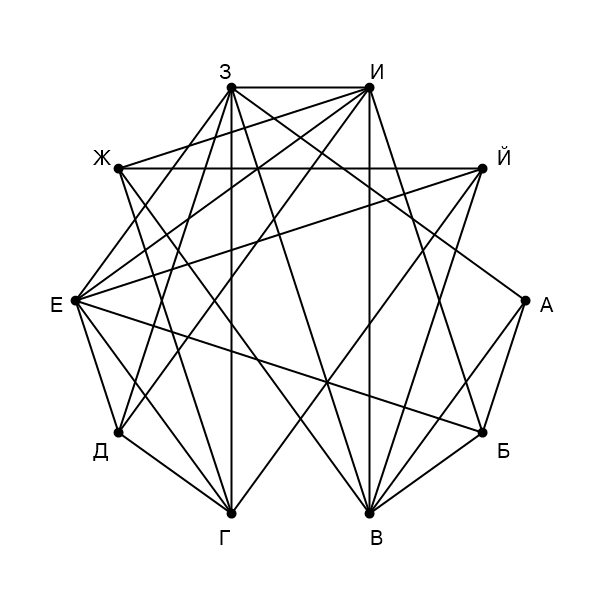

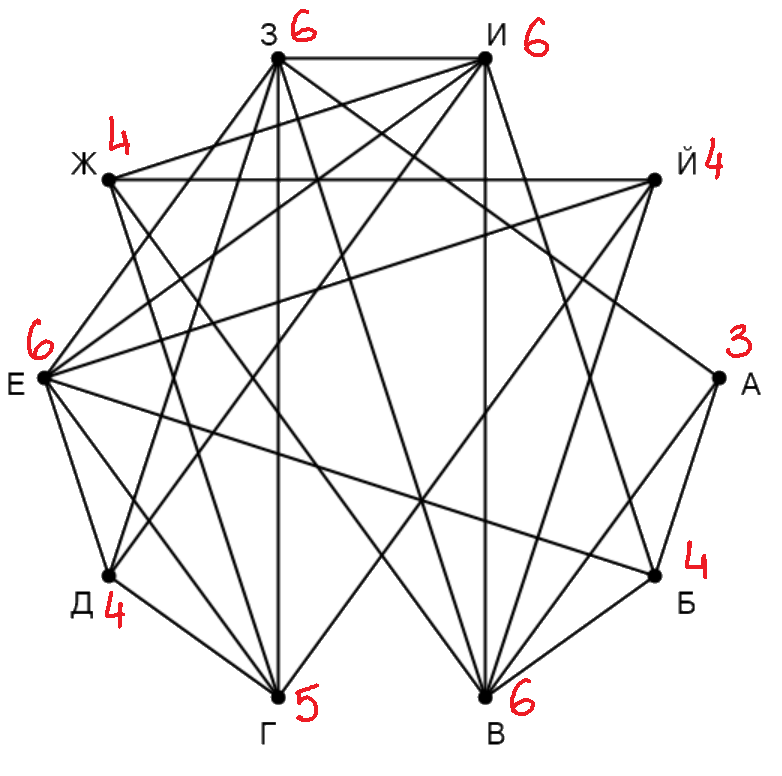
Расставим все степени (количество ребер, выходящих из нее) вершин: А - 3, Б - 4, В - 6, Г - 5, Д - 4, Е - 6, Ж - 4, З - 6, И - 6, Й - 4. У нас есть две вершины с уникальными степениями: А и Г, можем найти их по таблице: это вершины П5 и П3 соответственно. А связана с двумя вершинами степени 6 и одной вершиной степени 4, вершиной Б, эту вершину мы и можем найти по таблице через связи П5, это вершина П1. Б связана с тремя вершинами степени 6 из четырех, можем найти вершину, которая не связана с Б, степени 6, это вершина З, она же в таблице - П7. У нас осталось 3 вершины степени 4, две из которых связаны друг с другом, значит, можно найти вершину степени 4, не связанную ни с одной другой неизвестной вершиной степени 4, это вершина Д, она же в таблице П9. То же самое можно сделать с вершиной В и понять, что это П10. Осталось найти две вершины степени 6, одна из которых связана с З, другая нет, значит, по таблице через связи З ищем неизвестную вершину - это П6, она же вершина И. Значит, оставшаяся неизвестная вершина степени 6 - П2 - это Е. Две оставшиеся неизвестные можно найти по их связям: Й связана с Е, Г, В, а Ж связана с И, В, Г. Можно определить, что Й - это П4, а Ж - это П8.
Ошибка.
Попробуйте повторить позже
На рисунке схема дорог изображена в виде графа. В таблице звёздочками обозначено наличие дороги между населёнными
пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не
связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные
на графе буквенные обозначения пунктов от до
: сначала букву, соответствующую
, затем букву,
соответствующую
и т. д.
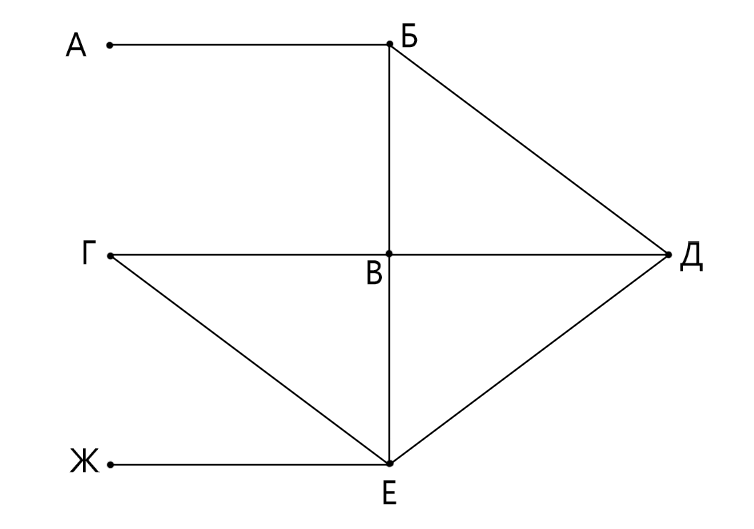
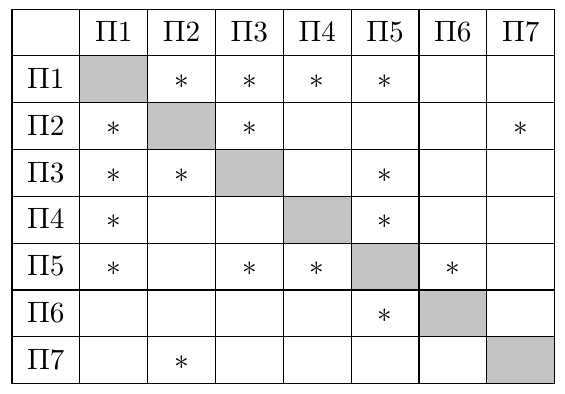
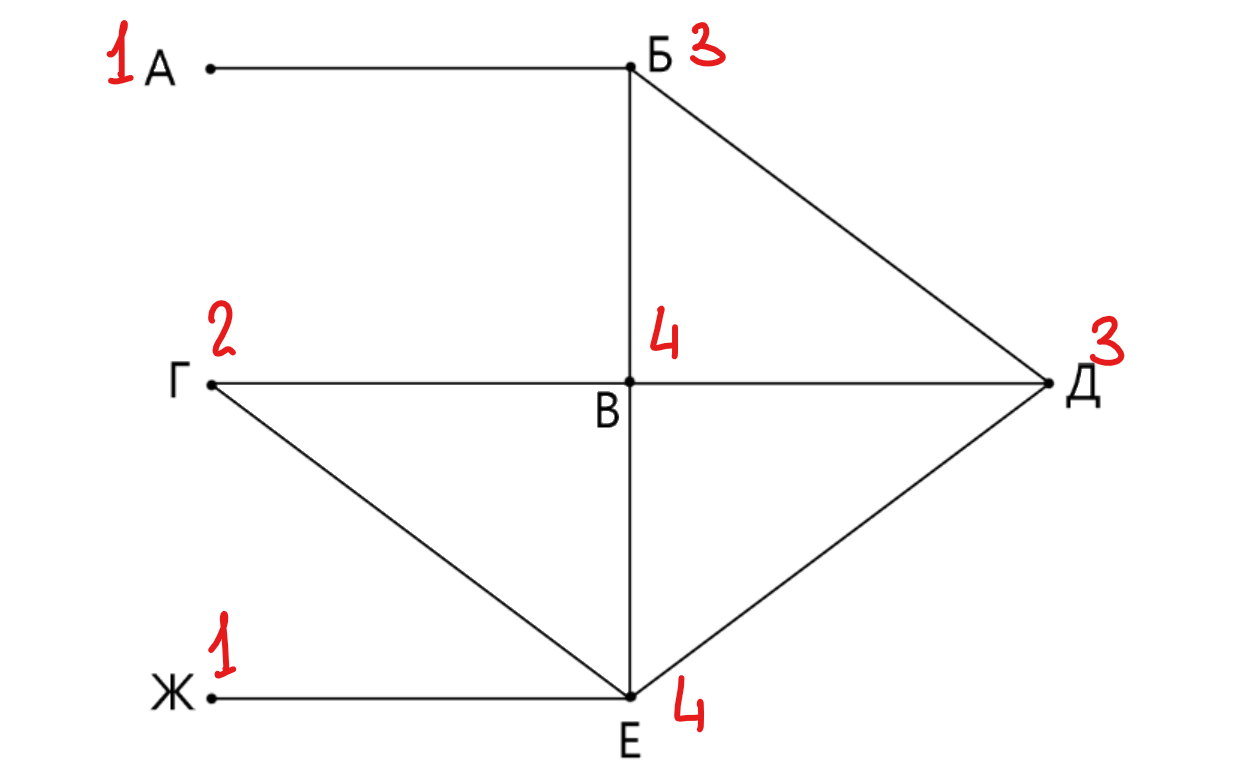
Распишем степени вершин. Видим, что — единственная вершина со степенью
. По матрице смежности устанавливаем,
что этой вершине соответствует
. Вершина
— единственная вершина со степенью
, которая связана с вершиной
со степенью
. По таблице смежности устанавливаем, что вершине
соответствует
, а вершине
—
.
Аналогично: вершина
— единственная вершина со степенью
, которая связана с вершиной
со
степенью
. По таблице смежности устанавливаем, что вершине
соответствует
, а вершине
—
. Оставшиеся две вершины —
со степенью
и
со степенью
. Им соответствуют
и
соответственно.



