Ошибка.
Попробуйте повторить позже
Объем правильной четырехугольной пирамиды равен 12. Точка
— середина ребра
Найдите объем
треугольной пирамиды
![]()
Пусть — площадь квадрата
— площадь треугольника
Тогда
Пусть — высота пирамиды
и
а
— высота пирамиды
Далее заметим, что
Тогда — средняя линия треугольника
так как
— середина
Отсюда
по углу и
отношению сторон
Тогда имеем:
![]()
Объем пирамиды вычисляется по формуле
Здесь — площадь основания пирамиды, а
— ее высота.
Тогда по условию имеем:
Вычислим объем пирамиды
Ошибка.
Попробуйте повторить позже
Найдите объем правильной треугольной пирамиды, сторона основания которой равна 6, а высота равна
В основании правильной пирамиды лежит правильный треугольник. Значит, площадь основания равна
Тогда объем пирамиды равен
Ошибка.
Попробуйте повторить позже
Найдите объем правильного тетраэдра, если одна из его апофем равна .

В правильном тетраэдре все грани являются равносторонними треугольниками. Высота тетраэдра
падает в точку пересечения медиан равностороннего треугольника (она же является точкой пересечения
биссектрис, высот и т.д.; далее в решении задачи нас будет интересовать точка пересечения медиан),
лежащего в основании.
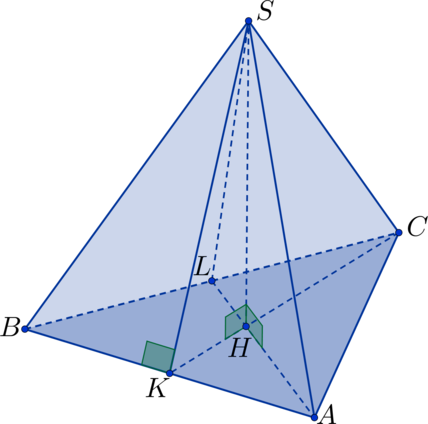
Пусть – правильный тетраэдр,
– апофема, лежащая в грани
. Она же является
медианой, проведенной к стороне
. Тогда, если ребро тетраэдра обозначить за
, то
высота
в равностороннем треугольнике выразится как
.
и
– медианы в треугольнике
,
– точка пересечения
и
,
– высота в тетраэдре. Медианы точкой пересечения делятся на отрезки,
состоящие в отношении
, где больший отрезок лежит между соответствующей вершиной
треугольника и точкой пересечения медиан. Тогда рассмотрим прямоугольный треугольник
:
, т.к. все равносторонние треугольники равны между собой и
следовательно также равны между собой их высоты.
, тогда найдем
по
теореме Пифагора:
. Наконец, найдем объем правильного
тетраэдра:
Ошибка.
Попробуйте повторить позже
В прямоугольной пирамиде
— высота пирамиды,
— прямоугольная трапеция с прямыми
углами
и
Найдите объем пирамиды, если
а

и
— прямоугольные треугольники, следовательно,
Таким образом,
Тогда можем найти площадь основания:
Значит,
Ошибка.
Попробуйте повторить позже
Объем правильной треугольной пирамиды равен . Найдите объем пирамиды, боковые ребра которой
являются апофемами исходной пирамиды.

Пусть – пирамида, боковые ребра которой являются апофемами исходной пирамиды
.
тоже является правильной пирамидой, так как вершины треугольника
являются
серединами сторон треугольника
, а значит стороны треугольника
являются
средними линиями треугольника
стороны треугольника
относятся к
соответствующим сторонам треугольника
как
их площади состоят в
отношении
. Высота искомой пирамиды совпадает с высотой исходной пирамиды
их
объемы относятся также, как их площади
объем искомой пирамиды равен
.
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида . На боковых рёбрах
,
и
отмечены точки
,
и
соотвественно так, что
,
и
. Найдите объём
если объём
равен 81.
![]()
Если то
Таким образом,
Если то
Таким образом,
Если то
Таким образом,
Воспользуемся формулой отношения объёмов для пирамид, имеющих равный трёхгранный угол:
Ошибка.
Попробуйте повторить позже
Найдите высоту правильной четырехугольной пирамиды с основанием 40 и боковым ребром 30.
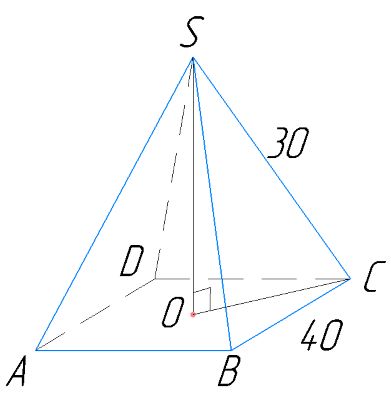
Длина отрезка равна половине длины диагонали квадрата
Диагональ
квадрата
тогда
В прямоугольном треугольнике
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с основанием
боковое
ребро
равно 17, сторона основания равна
Найдем объем пирамиды.
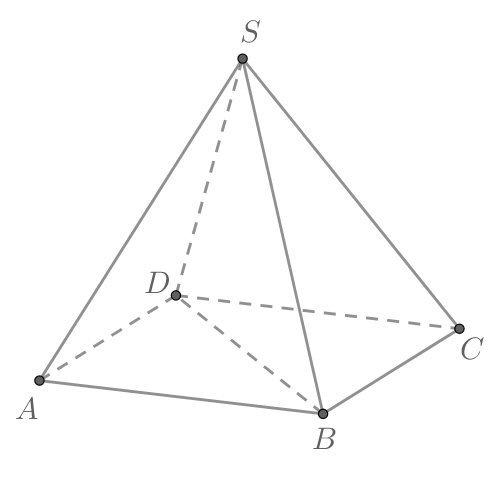
Пусть — точка пересечения диагоналей квадрата
Тогда
—
высота пирамиды. Следовательно,
— прямоугольный. Так как
а
то по теореме Пифагора
Следовательно, объем пирамиды равен
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде точка
— центр
основания,
— вершина,
Найдите длину отрезка
Так как пирамида правильная, то — высота пирамиды. Следовательно,
прямоугольный, значит, по теореме Пифагора
Так как пирамида правильная, то в основании лежит квадрат, следовательно,
его диагонали равны, причем точкой делятся пополам, значит,
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с высотой через точку на боковом
ребре, лежащую на расстоянии
от плоскости основания, проведена плоскость,
параллельная плоскости основания, которая отсекает от пирамиды меньшую
пирамиду. Найдите объем полученной меньшей пирамиды, если объем исходной
пирамиды равен 54.
Пусть плоскость провели через точку на ребре
Так как эта плоскость
параллельна плоскости основания, то она пересечет боковые грани по
прямым
, параллельным соответственно прямым
При этом
— тоже правильная четырехугольная
пирамида.
Рассмотрим плоскость Проведем
где
— высота
исходной пирамиды. Тогда
Следовательно, это и есть расстояние,
равное
на котором от плоскости основания проведена плоскость
Так как то имеем:
Также отсюда следует, что
Так как то
Таким образом, объемы маленькой и большой пирамид относятся как
Следовательно, объем маленькой пирамиды равен
Ошибка.
Попробуйте повторить позже
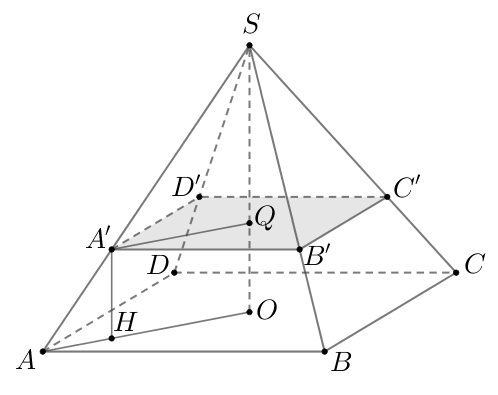
Дана правильная четырехугольная пирамида, объем которой равен . Найдите объем пирамиды,
вершина которой совпадает с вершиной исходной пирамиды, а вершины основания совпадают с
серединами сторон основания исходной пирамиды.
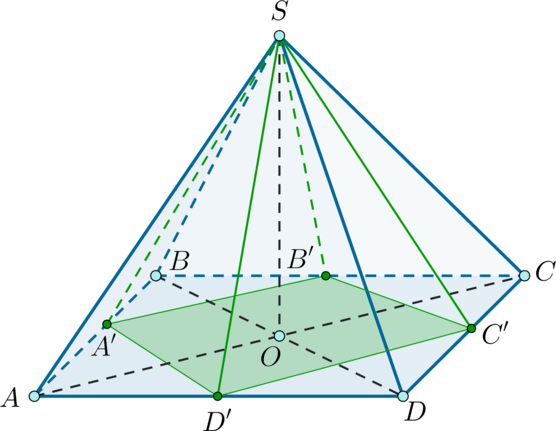
Рассмотрим рисунок. Пусть – исходная пирамида,
– середины отрезков
соответственно.
– высота пирамиды
.
Так как
Ошибка.
Попробуйте повторить позже
Пирамида прямоугольная,
– высота пирамиды. Точки
,
,
лежат соответственно
на сторонах
,
,
, причем
,
, а
. Найдите
площадь поверхности пирамиды
, если площадь поверхности пирамиды
равна
.
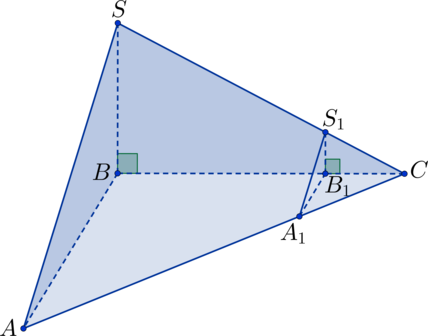
Треугольник и
подобны, т.к. у них общий угол
и по теореме Фалеса
параллельные стороны
и
отсекают пропорциональные отрезки. Аналогичным
образом подобны треугольники
и
. Тогда из пропорциональности
соответствующих сторон вытекает подобие треугольников
,
, соответственно
треугольникам
,
. Коэффициент подобия
. Тогда
Ошибка.
Попробуйте повторить позже
– прямоугольная пирамида (отрезок
перпендикулярен плоскости основания
),
– параллелограмм со сторонами
,
, причем
Построим перпендикулярно
, как показано на рисунке.
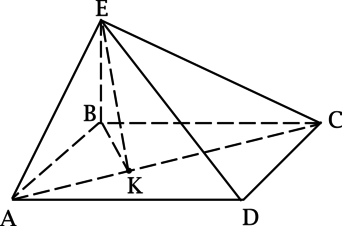
Так как – проекция
на плоскость
, то по теореме о трех перпендикулярах
перпендикулярен
, следовательно, угол между плоскостями
и
есть
.
Найдем :
рассмотрим параллелограмм . С одной стороны, его площадь
Приравняв площади параллелограмма, получим:
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с вершиной
. Угол между боковым ребром и
стороной основания равен
, а
. Найдите площадь боковой поверхности этой пирамиды.
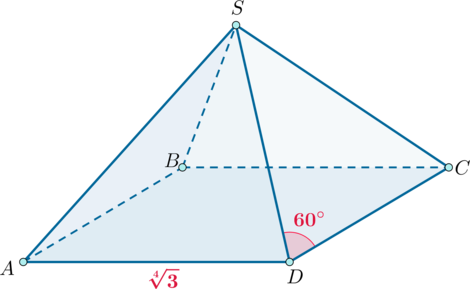
Так как пирамида правильная, то все боковые грани представляют собой равные равнобедренные
треугольники. Так как у них угол при основании равен , то они являются равносторонними, то есть
все боковые ребра пирамиды равны стороне основания. Площадь правильного треугольника со стороной
вычисляется по формуле
, следовательно, площадь боковой поверхности
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с вершиной
. Известно, что боковое ребро пирамиды
равно
, а угол между боковым ребром и плоскостью основания
. Найдите объем пирамиды.
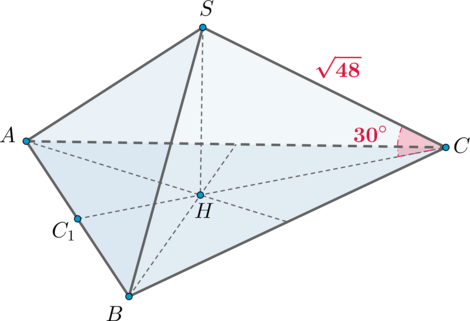
Пусть – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания,
то есть в точку пересечения медиан (высот, биссектрис).
Заметим, что .
Пусть – высота (а значит и медиана) основания. Тогда
Так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость, а
Из прямоугольного
Следовательно, объем пирамиды равен
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с вершиной
. Известно, что сторона основания
пирамиды равна
, а угол между ее высотой и боковым ребром равен
. Найдите объем
пирамиды.
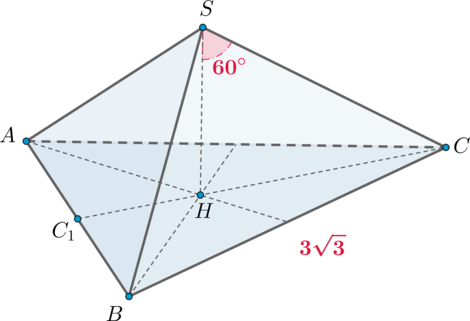
Пусть – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания,
то есть в точку пересечения медиан (высот, биссектрис).
Пусть – высота (а значит и медиана) основания. Тогда
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с основанием
, сторона которого равна
.
Найдите объем пирамиды, если угол
равен
.
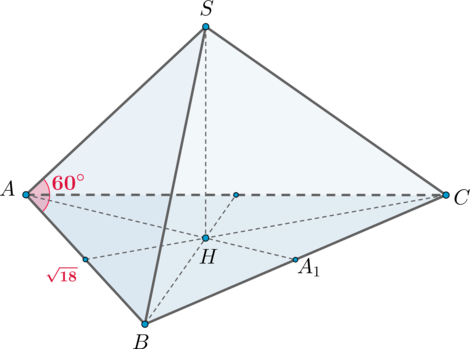
Пусть – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания,
то есть в точку пересечения медиан (высот, биссектрис). Также боковые грани представляют собой
равнобедренные треугольники. Так как в равнобедренном
угол при основании равен
, то
треугольник равносторонний, следовательно,
.
Пусть – высота основания. Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите апофему в правильной шестиугольной пирамиде, если сторона шестиугольника равна , а
тангенс угла наклона бокового ребра к основанию равен
.
– правильная шестиугольная пирамида,
– высота пирамиды,
–
правильный шестиугольник.
– равносторонний треугольник
. Рассмотрим
треугольник
:
– перпендикуляр,
– наклонная к плоскости шестиугольника,
– проекция
наклонной
.
– высота в равностороннем
треугольнике
. Тогда апофему можно найти из прямоугольного
треугольника
по теореме Пифагора:
.
Ошибка.
Попробуйте повторить позже
Высота правильной треугольной пирамиды равна , а двугранный угол при основании равен
.
Найдите объем пирамиды.
Так как пирамида правильная, то высота падает в точку пересечения медиан (которые являются
также высотами и биссектрисами) основания. Пусть
. Тогда
. Тогда по теореме о
трех перпендикулярах наклонная
, проекцией которой является
, также будет
перпендикулярна
. Следовательно,
– линейный угол двугранного угла при основании, то
есть
.
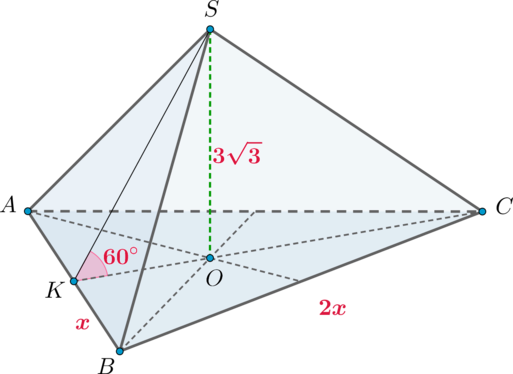
Из прямоугольного :
Пусть
Ошибка.
Попробуйте повторить позже
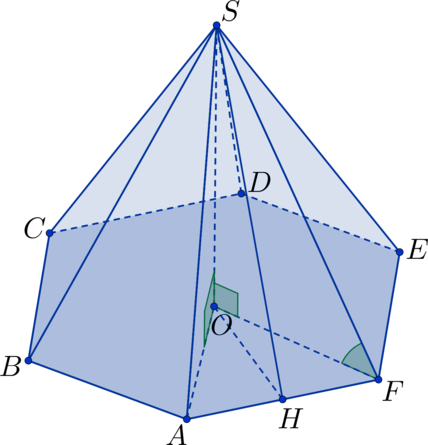
– правильная пирамида (
– шестиугольник),
, площадь полной
поверхности пирамиды равна
. Найдите расстояние от точки
до плоскости
.
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из этой точки на плоскость.
Так как в основании пирамиды правильный шестиугольник, то
Тогда суммарная площадь оставшихся граней пирамиды равна . Так как у
правильной пирамиды все грани – равные треугольники, то площадь каждой боковой грани равна
, откуда с учётом того, что
находим высоту треугольника
: она равна
2.
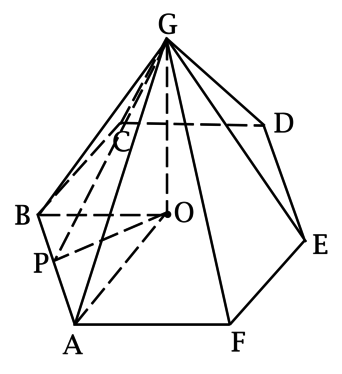
Так как – правильная пирамида, то точка
– основание перпендикуляра,
опущенного из точки
на плоскость
– центр описанной около
окружности,
.
Пусть высота в треугольнике
, тогда
,
, но треугольник
–
равнобедренный, тогда
– высота (в нём) и, значит,
.
По теореме Пифагора



