Ошибка.
Попробуйте повторить позже
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
![]()
Пусть площадь основания пирамиды равна а ее высота равна
Тогда объём пирамиды равен
Если высоту пирамиды увеличили в 4 раза, то и ее объем увеличился в 4 раза:
Ошибка.
Попробуйте повторить позже
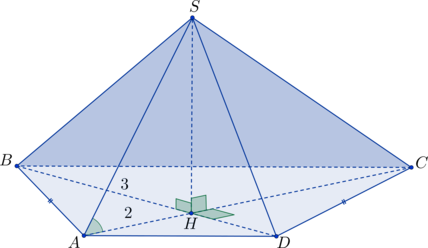
В основании пирамиды лежит прямоугольный треугольник с прямым углом
.
Точка
– центр описанной вокруг треугольника
окружности,
– высота
пирамиды. Найдите объем пирамиды, если известно, что
,
,
.
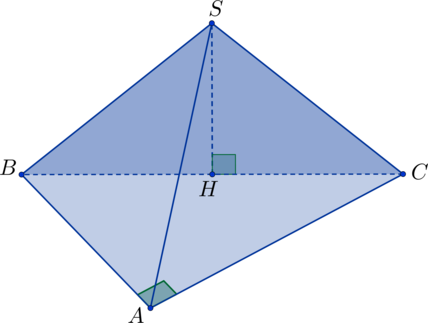
Центр описанной вокруг прямоугольного треугольника окружности лежит на гипотенузе и делит
ее пополам – радиусы описанной окружности. В прямоугольном
треугольнике
по теореме Пифагора:
. Треугольник
– прямоугольный, т.к.
(
– высота), тогда
по теореме Пифагора можно найти
:
.
Теперь найдем объем пирамиды:
Ошибка.
Попробуйте повторить позже
Объем треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию ее основания проведена плоскость. Найдите объем отсеченной треугольной пирамиды.
Средняя линия треугольника отсекает от него треугольник, подобный данному с
коэффициентом подобия Тогда площадь отсекаемого треугольника в 4 раза
меньше площади исходного треугольника.
Высоты исходной пирамиды и отсеченной, проведенные к плоскости этого треугольника, одинаковы. Следовательно, объем отсеченной пирамиды в 4 раза меньше объема исходной пирамиды:
Ошибка.
Попробуйте повторить позже
В основании пирамиды лежит равнобедренная трапеция
,
– большее основание.
Высота пирамиды падает на отрезок
. Апофема грани
равна
и образует угол
с
плоскостью трапеции. Найдите объем пирамиды, если средняя линия трапеции равна
.
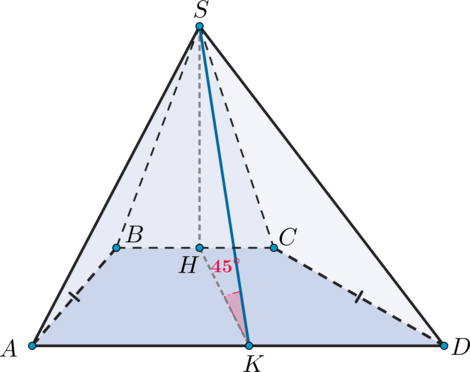
Пусть – высота пирамиды. Проведем
. Следовательно, по теореме о трех
перпендикулярах
(наклонная) также перпендикулярна
(так как
– ее проекция на
плоскость
). Следовательно,
и есть апофема грани
. Также отсюда следует,
что
(так как угол между прямой и плоскостью – это угол между прямой и
ее проекцией на плоскость). Следовательно,
прямоугольный и равнобедренный,
значит,
Ошибка.
Попробуйте повторить позже
– пирамида,
,
, проекция точки
на плоскость
– середина
. Длина отрезка, соединяющего точку
и середину
, равна
, площадь полной поверхности пирамиды равна
. Найдите
.
Так как , то
, тогда
–
прямоугольник, но
, следовательно,
– квадрат.
Обозначим отрезок, соединяющий точку и середину
через
.
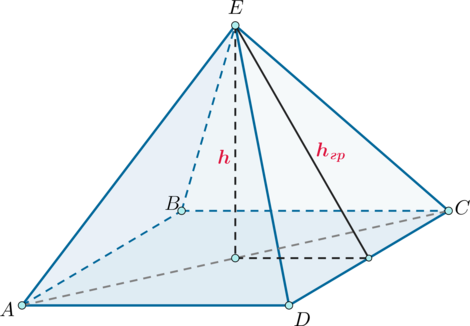
Так как – квадрат, то
соединяет точку
с серединой
, то есть проекцией точки
на
, откуда заключаем, что
перпендикулярен
. Через
обозначим перпендикуляр,
опущенный из точки
на
.
Пирамида является правильной по определению. Тогда её грани равные равнобедренные
треугольники и площадь её полной поверхности равна
.
По теореме Пифагора
По теореме Пифагора
Ошибка.
Попробуйте повторить позже
– пирамида,
– прямоугольник со сторонами
и
. Из точки
опущен перпендикуляр
на плоскость
, причём точка
попала на
так,
что
. Пусть
– площадь поверхности пирамиды
. Найдите
.
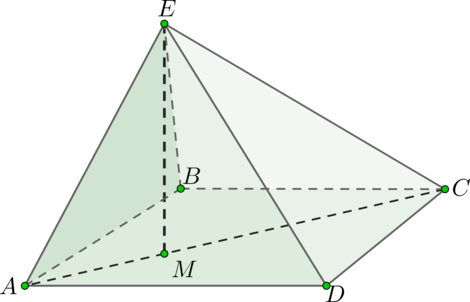
Пусть . Рассмотрим прямоугольник
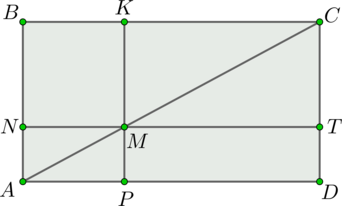
Достроим отрезки и
, проходящие через точку
, как показано на рисунке (
,
).
Тогда ,
,
,
.
– проекция
на
,
перпендикулярен
, тогда по теореме о трех перпендикулярах
перпендикулярен
. По
теореме Пифагора
. Площадь треугольника
равна
площадь треугольника
площадь треугольника
площадь прямоугольника
Площадь поверхности пирамиды:
Ошибка.
Попробуйте повторить позже
– пирамида,
– параллелограмм со сторонами
и
,
.
Из точки
опущен перпендикуляр
на плоскость
, причём точка
–
точка пересечения диагоналей
,
. Найдите объем пирамиды.
Объем пирамиды может быть найден по формуле , где
– площадь основания пирамиды,
– высота пирамиды.
Площадь параллелограмма может быть найдена по формуле , где
,
– не
параллельные стороны параллелограмма,
– угол между ними.
Найдем :
по теореме Пифагора для треугольника :
Так как диагонали параллелограмма точкой пересечения делятся пополам, то .
Найдем по теореме косинусов для треугольника
:
Ошибка.
Попробуйте повторить позже
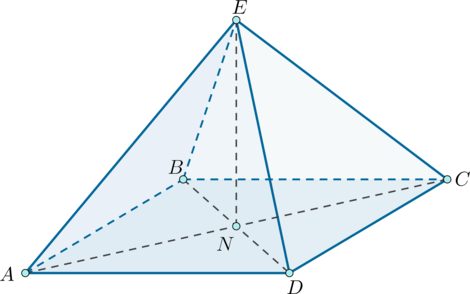
В основании пирамиды лежит равнобедренная трапеция с основаниями
и
.
–
точка пересечения диагоналей трапеции, а
– высота пирамиды. Диагонали трапеции
перпендикулярны,
,
,
. Найдите объем пирамиды.
и
– равнобедренные треугольники, т.к. трапеция
равнобедренная
,
В :
, т.к.
– прямоугольный. Тогда объем пирамиды можно
найти следующим образом:
Ошибка.
Попробуйте повторить позже
Высота треугольной пирамиды
падает на середину стороны
,
– правильный
треугольник со стороной
. Найдите объем пирамиды, если
.
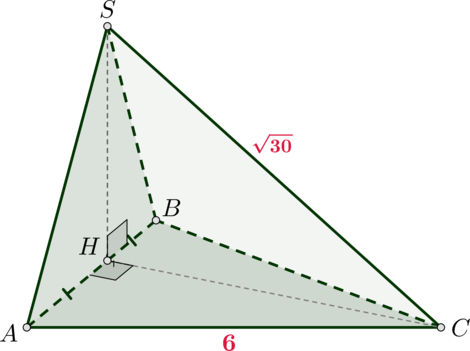
Так как – середина
и треугольник правильный, то
– высота. Следовательно,
Ошибка.
Попробуйте повторить позже
В пирамиде высота
падает в точку пересечения медиан основания. Треугольник
равнобедренный, боковые стороны равны
, а основание
. Найдите объем пирамиды,
если известно, что угол между боковым ребром
и плоскостью основания равен
.
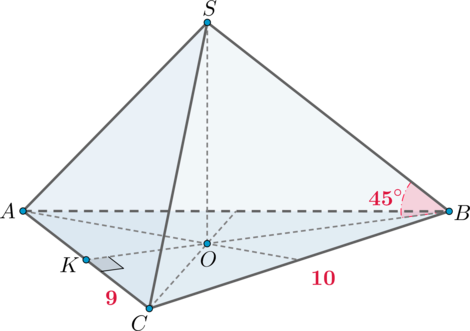
Пусть – высота в
, а значит и медиана. Тогда из прямоугольного
:
Ошибка.
Попробуйте повторить позже
Дана пирамида , вершиной которой является точка
, в основании лежит ромб, а высота
пирамиды падает в точку пересечения диагоналей ромба. Найдите объем пирамиды,
если известно, что угол
равен углу
, а диагонали основания равны
и
.
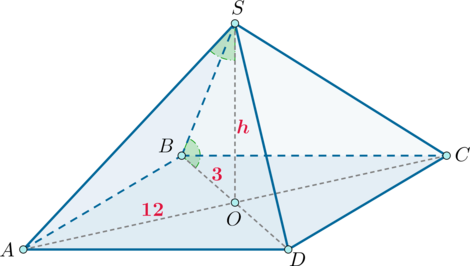
Так как диагонали ромба точкой пересечения делятся пополам, то ,
.
Заметим, что так как – высота пирамиды, то
и
– прямоугольные.
Так как у них есть равные острые углы, то они подобны. Пусть
, тогда из подобия
имеем:
Ошибка.
Попробуйте повторить позже
– треугольная пирамида,
. Плоскость
. Сечение
плоскостью
есть треугольник
, причём
, а высота пирамиды
, проведённая из вершины
к
, равна
. Найдите
.
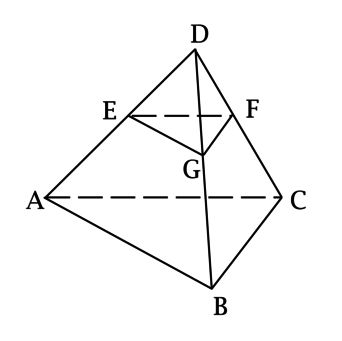
Так как , то треугольники
и
подобны. Так как
, то
.



