Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида объемом 40. Через вершину
и середину
ребра
проведена плоскость, пересекающая ребро
в точке
Расстояние от вершины
до этой плоскости равно 4, а площадь треугольника
равна 5.
а) Докажите, что точка делит ребро
в отношении
считая от
точки
б) Найдите угол между плоскостью сечения и плоскостью пирамиды,
если дополнительно известно, что ребро
перпендикулярно плоскости
и
равно 15.
а) Из условия следует, что Объемы тетраэдров, имеющих
общий трехгранный угол, относятся как произведения ребер, образующих этот
трехгранный угол. Следовательно,
Чтд.

б) По условию — высота тетраэдра
Следовательно,
Так как медиана треугольника делит его на два равновеликих треугольника,
то
— проекция
на плоскость
Следовательно, косинус угла между плоскостями
и
равен
б)
Ошибка.
Попробуйте повторить позже
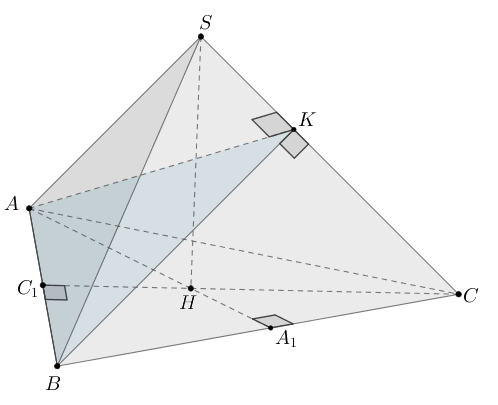
В правильной треугольной пирамиде проведено сечение плоскостью,
проходящей через сторону основания
перпендикулярно ребру
а) Докажите, что площадь сечения относится к площади основания пирамиды так же, как высота пирамиды относится к ее боковому ребру.
б) Найдите площадь сечения пирамиды, если боковое ребро а сторона
основания
а) Пусть — сечение пирамиды
плоскостью, перпендикулярной
и проходящей через
Так как
то
— высота пирамиды
Объемы тетраэдров, имеющих общий трехгранный угол, относятся как произведения ребер, образующих этот трехгранный угол. Следовательно,
С другой стороны,
Отсюда
Чтд.
б) Из пункта а) следует, что
Высота правильного треугольника со стороной равна
следовательно,
а
Тогда по теореме Пифагора
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
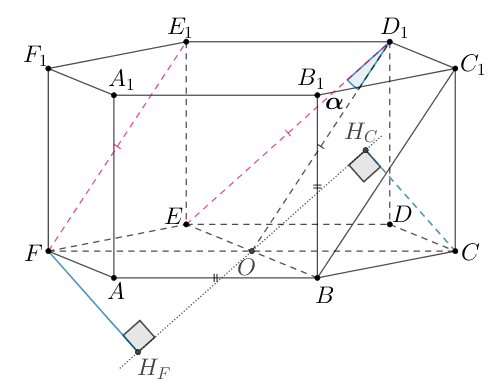
В правильной шестиугольной призме все ребра равны
1.
а) Докажите, что точки и
равноудалены от плоскости
б) Найдите расстояние между прямыми и
а) Так как плоскость пересекает две параллельные плоскости по параллельным
прямым, то плоскость плоскость
пересечет по прямой
Пусть
Тогда
— центр правильного
шестиугольника, следовательно,
Пусть
и
—
перпендикуляры из точек
и
на плоскость
соответственно. Тогда
как прямоугольные по гипотенузе и острому углу
(
как вертикальные). Следовательно,
Чтд.
В задаче 41859 была доказана формула
где — противоположные ребра тетраэдра,
— расстояние между ними,
— угол между ними. Будем пользоваться этой формулой, чтобы найти
расстояние между ребрами
и
тетраэдра
В наших обозначениях объем этого тетраэдра равен
где — угол между
и
Заметим, что отрезки и
равны
Так как
и
то
— параллелограмм, следовательно,
следовательно,
— угол между
и
Найдем его по теореме
косинусов из
где
С другой стороны, объем тетраэдра равен
по формуле, которая доказывалась в задаче 41979 ( и есть угол
между гранями
и
).
Заметим, что Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной призме со стороной основания
и высотой 7 на ребре
взята точка
так, что
На ребре
взята точка
так, что
Найдите угол между плоскостями
и
Так как то можно искать угол между плоскостью
и
плоскостью
Назовем этот угол
В задаче 41979 была доказана формула
для объема треугольной пирамиды, где и
— площади двух граней,
—
их общее ребро,
— угол между плоскостями этих граней.
Если рассмотреть тетраэдр то его объем равен
С другой стороны, его объем равен
Отсюда

- Пусть
— проекция
на
Тогда
следовательно,
-
Рассмотрим
Его полупериметр равен
Следовательно, по формуле Герона его площадь равна
Следовательно,
Ошибка.
Попробуйте повторить позже
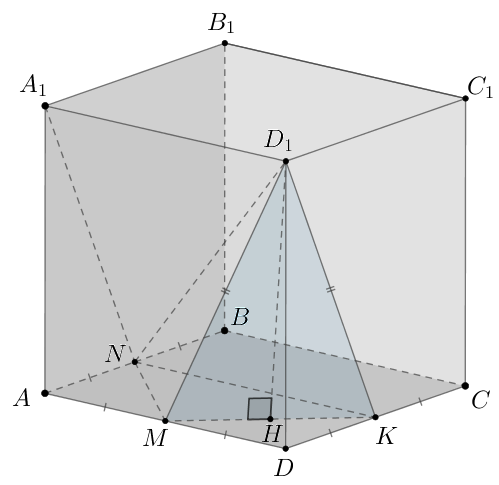
Точки и
— середины ребер
и
соответственно куба
Найдите расстояние между прямыми
и
если
ребро куба равно 6.
Пусть — середина
Тогда
Следовательно, расстояние
между прямыми
и
равно расстоянию от любой точки прямой
до плоскости
Пусть
— расстояние от точки
до этой
плоскости. Рассмотрим тетраэдр
Запишем его объем двумя
способами:
Пусть
Так как
равнобедренный, то
и
— прямоугольные и равнобедренные, следовательно,
Тогда
Следовательно,
— прямоугольный и равнобедренный.
Тогда
4
Ошибка.
Попробуйте повторить позже
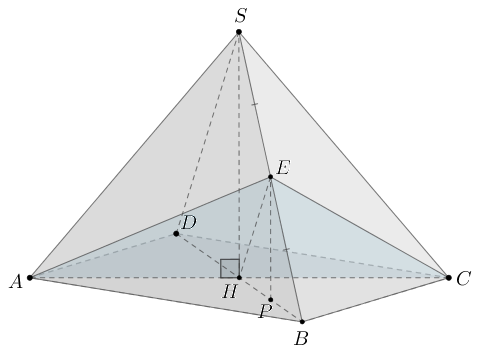
В правильной четырехугольной пирамиде с вершиной
все ребра
которой равны 1, точка
— середина бокового ребра
Найдите расстояние
от точки
до плоскости
Пусть — расстояние от точки
до плоскости
Рассмотрим тетраэдр
Пусть
— высота пирамиды
следовательно,
— высота тетраэдра
причем, так как
— середина
то
и
Запишем объем тетраэдра двумя разными способами:
Так как то по теореме о трех перпендикулярах
Следовательно,
— высота
Но
— медиана прямоугольного
треугольника
проведенная к гипотенузе. Следовательно,
Следовательно,
Ошибка.
Попробуйте повторить позже
В тетраэдре грани
и
имеют площади
и
и образуют
между собой угол
Найдите площадь сечения, проходящего через ребро
и
центр вписанного в тетраэдр шара.
В задаче 41979 была доказана формула
для объема треугольной пирамиды, где и
— площади двух граней,
—
их общее ребро,
— угол между плоскостями этих граней. Если обозначить
то по этой формуле объем тетраэдра
равен
Заметим, что центр шара, вписанного в тетраэдр, лежит на пересечении
биссекторных плоскостей тетраэдра. Следовательно, плоскость — биссектор,
то есть делит двугранный угол, образованный гранями
и
пополам.
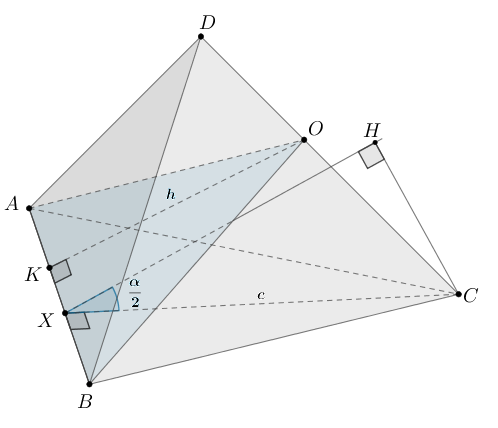
В задаче 46419 в ходе решения была доказана формула
где
Проведем Пусть
тогда по теореме о трех
перпендикулярах
Следовательно,
Пусть
— высота
проведенная к
Тогда
и
Тогда из получаем равенство
(так как )
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная призма в которой
Найдите расстояние между прямыми
и
Проведем Тогда расстояние между прямыми
и
равно
расстоянию от любой точки прямой
до плоскости
Пусть
—
расстояние от точки
до этой плоскости. Рассмотрим тетраэдр
Запишем его объем двумя способами:

равнобедренный с основанием
Пусть
Тогда, так
как
имеем:
Тогда
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная призма в которой
Найдите расстояние от точки
до плоскости
где
—
точка пересечения диагоналей основания
Пусть и
— перпендикуляры на плоскость
Тогда
с коэффициентом подобия
Следовательно,
Будем искать
Рассмотрим тетраэдр Его объем равен
от объема параллелепипеда.
Действительно,
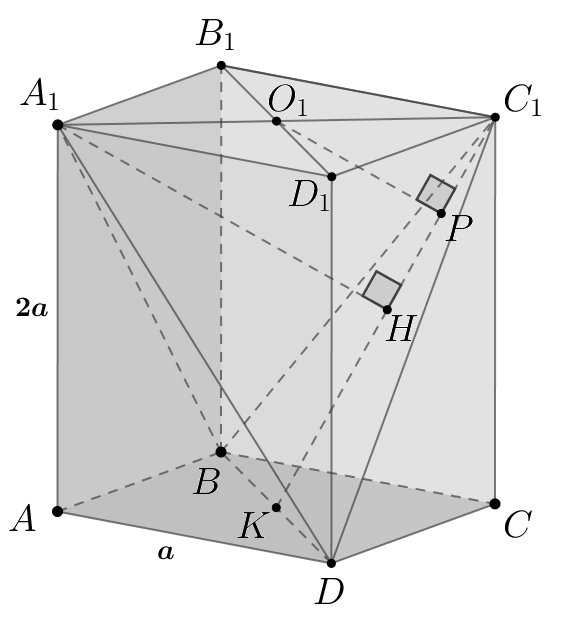
С другой стороны, если обозначить за расстояние от точки
до плоскости
объем этого тетраэдра равен
Следовательно,
-
равнобедренный с основанием
Пусть
Тогда, так как
имеем:
Следовательно,
Ошибка.
Попробуйте повторить позже
Докажите, что биссектор двугранного угла при ребре тетраэдра делит противоположное ребро на части, пропорциональные площадям граней тетраэдра, лежащих на гранях этого угла.
Пусть — тетраэдр, плоскость
— биссекторная плоскость,
Пусть
Докажем,
что
Проведем перпендикуляры
Проведем также
Тогда по ТТП
Тогда
так как это линейные углы двугранных углов, образованных биссекторной
плоскостью и гранями двугранного угла. Следовательно, по острому углу и общей
гипотенузе
Отсюда
Следовательно, если
обозначить за
то
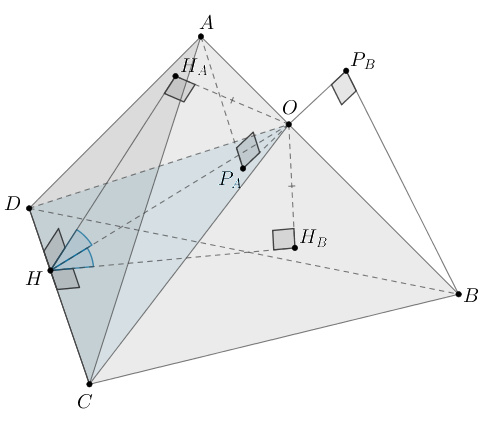
Проведем теперь
Тогда
Но точки лежат на одной прямой и
причем
Следовательно, получаем нужное равенство
Ошибка.
Попробуйте повторить позже
Длина ребра прямоугольного параллелепипеда
равна
угол
равен
а угол
равен
Найдите расстояние между
прямыми
и
Так как то расстояние между прямыми
и
равно
расстоянию от любой точки прямой
до плоскости
Пусть
—
расстояние от
до этой плоскости. Рассмотрим тетраэдр
. Запишем
его объем двумя способами:

-
-
Пусть
Следовательно,
Тогда
Следовательно,
Тогда
Ошибка.
Попробуйте повторить позже
Длина ребра прямоугольного параллелепипеда
равна
угол
равен
а угол
равен
Найдите расстояние от точки
до плоскости
Рассмотрим тетраэдр Его объем равен
от объема параллелепипеда.
Действительно,
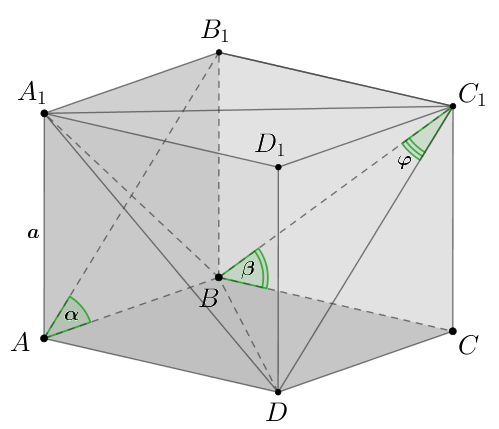
С другой стороны, если обозначить за расстояние от точки
до плоскости
объем этого тетраэдра равен
Следовательно,
-
-
Пусть
Следовательно,
Тогда
Следовательно,
Тогда
Ошибка.
Попробуйте повторить позже
В кубе с ребром, равным 3, найдите расстояние между
прямыми
и
Проведем Тогда
следовательно, расстояние между
прямыми
и
равно расстоянию между прямой
и плоскостью
а оно в свою очередь равно расстоянию от любой точки прямой
до
этой плоскости.
Пусть — расстояние от точки
до плоскости
Рассмотрим
тетраэдр
Запишем его объем:

-
— равносторонний, его стороны равны диагоналям квадратов со стороной 3. Так как
то
Следовательно,
Ошибка.
Попробуйте повторить позже
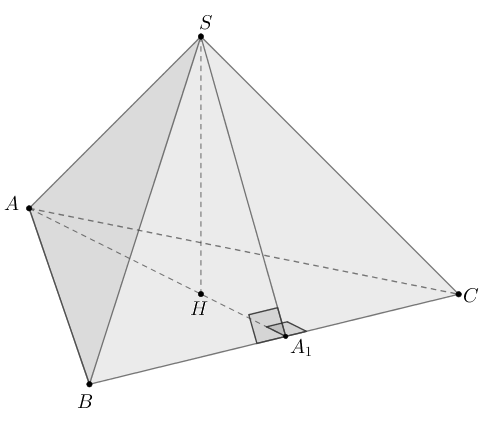
В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найдите отношение радиуса вписанного в пирамиду шара к стороне основания пирамиды.
Пусть боковое ребро пирмиды равно высота пирамиды
сторона
основания равна
а радиус вписанного в пирамиду шара равен
Запишем
объем пирамиды
двумя разными способами:
Пусть Тогда по теореме Пифагора
следовательно,
Так как высота правильного треугольника равна
то
Следовательно,
Следовательно, по теореме Пифагора
Тогда
Следовательно,
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной призме сторона основания
а боковое ребро
Точка
— середина ребра
Найдите
расстояние от точки
до плоскости
Пусть — расстояние от точки
до плоскости
Рассмотрим тетраэдр
Запишем его объем:
По теореме Пифагора
Пусть
Так
как
равнобедренный, то
Следовательно, по теореме Пифагора
Следовательно,
Ошибка.
Попробуйте повторить позже
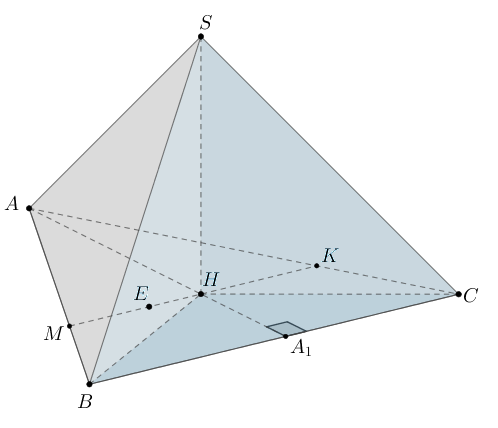
В правильной треугольной пирамиде с вершиной
на сторонах
и
выбраны точки
и
соответственно так, что треугольник
подобен треугольнику
с коэффициентом подобия
На прямой
выбрана точка
так, что
Найдите расстояние от точки
до
плоскости
если сторона основания пирамиды равна 6, а высота пирамиды
равна
Так как равносторонний, то
также равносторонний,
следовательно,
как соответственные, значит,
Из условия следует, что
Пусть — высота основания, тогда если
— высота пирамиды, то
По обратной теореме Фалеса, так как
имеем
Следовательно,
Заметим, что так как то
следовательно, то
расстояние от любой точки прямой
до плоскости
будет одинаковым.
Пусть
— расстояние от точки
до плоскости
Запишем объем
пирамиды
двумя разными способами:
Так как высота правильного треугольника со стороной равна
то
Тогда
По теореме Пифагора апофема
Следовательно,
Ошибка.
Попробуйте повторить позже
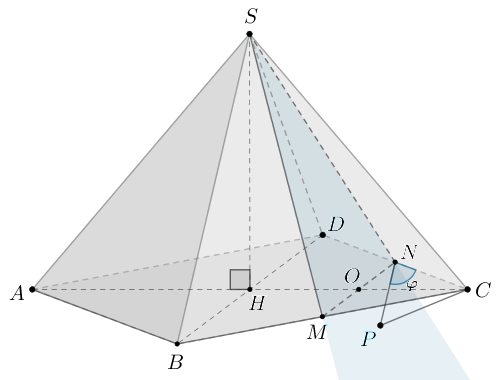
В правильной четырехугольной пирамиде с вершиной
со стороной
основания, равной
и боковым ребром, равным 5, найдите угол между прямой
и плоскостью, проходящей через середины
и
и вершину
Пусть и
— середины
и
соответственно. Назовем плоскость
плоскостью
Так как
то угол между
и
равен углу
между
и
Проведем
Тогда
— проекция
на
Следовательно,
Найдем Запишем объем пирамиды
двумя разными способами:
где — высота пирамиды
Вычислим нужные величины.
и
Следовательно,
Тогда
Ошибка.
Попробуйте повторить позже
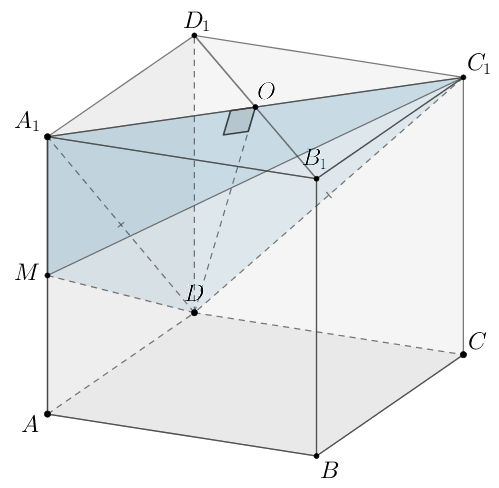
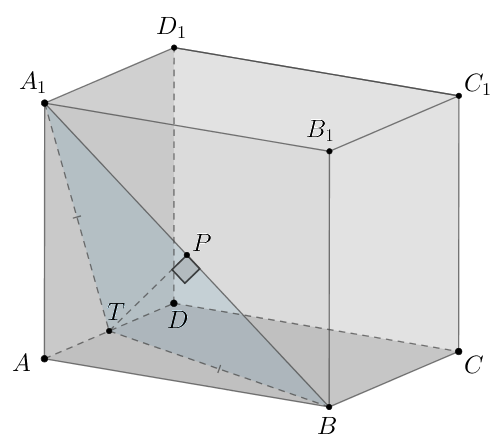
Дан куб с ребром 1,
— середина ребра
а) Докажите, что объем пирамиды в 12 раз меньше объема
куба.
б) Найдите расстояние от вершины до плоскости
а) Объем куба равен Объем пирамиды
равен
б) Запишем объем пирамиды двумя разными способами, обозначив за
искомое расстояние от точки
до плоскости
Заметим, что как прямоугольные по двум катетам.
Следовательно,
значит,
равнобедренный. Пусть
— его
высота, проведенная к основанию. По теореме Пифагора
Следовательно,
Тогда
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
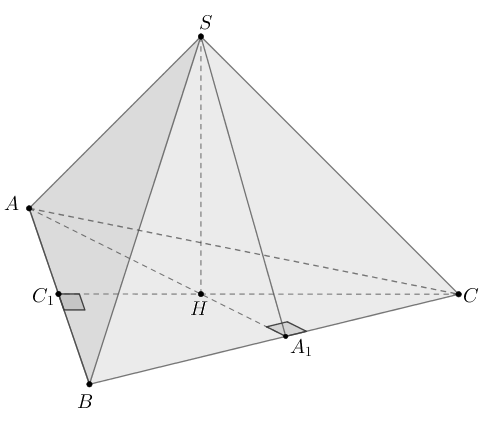
В правильной треугольной пирамиде с основанием
боковое ребро
равно 5, а сторона основания равна 6.
а) Докажите, что
б) Найдите расстояние от вершины до плоскости
а) Пусть и
— высоты основания пирамиды, которые пересекаются в
точке
Тогда
— высота пирамиды.
— проекция наклонной
на
плоскость
Следовательно, так как
по теореме о трех
перпендикулярах
б) Объем пирамиды равен
где — искомое расстояние от точки
до плоскости
- Высота правильного треугольника со стороной
равна
следовательно,
-
По теореме о трех перпендикулярах
По теореме Пифагора
Следовательно,
Тогда
-
Площадь правильного треугольника со стороной
равна
следовательно,
Тогда
б)
Ошибка.
Попробуйте повторить позже
Плоскость пересекает боковые ребра и
треугольной пирамиды
в
точках
и
соответственно и делит объем пирамиды пополам.
а) Постройте сечение пирамиды плоскостью, если
б) В каком отношении эта плоскость делит медиану грани
а) Докажем, что плоскость, которую мы назовем пересекает ребро
Для этого покажем, что плоскость
отсекает от пирамиды
пирамиду
объем которой больше половины объема пирамиды
Так как объемы треугольных пирамид с общим трехгранным углом относятся как произведения ребер, выходящих из вершины этого трехгранного угла, то
Следовательно, плоскость пересекает ребро
Пусть она его пересекает в
точке
Определим положение точки
на ребре
Тогда по той же самой
теореме
Сечение пирамиды плоскостью определено и построено.
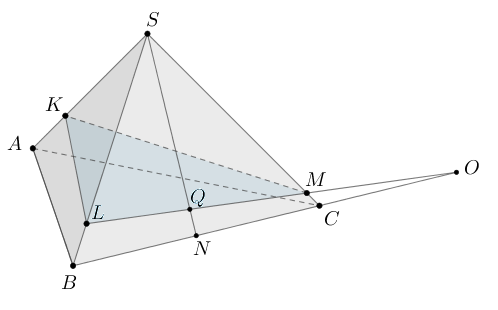
б) Пусть плоскость пересекает
в точке
Пусть прямая
пересекается с прямой
в точке
Запишем теорему Менелая для
и
прямой
Следовательно, можно принять
Тогда по теореме
Менелая для
и прямой
б)



