Поиск наибольшего/наименьшего значения у элементарных функций —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#17167

Найдите наименьшее значение функции $3 y = 13+ 75x − x$ на отрезке $[−5;5].$

Показать ответ и решение

Для того, чтобы найти наименьшее значение функции на отрезке, нужно схематично изобразить график функции.

1.

Найдем производную:

y′ = 75− 3x2

2.

Найдем нули производной:

75− 3x2 = 0 ⇒ x= ±5

3.

Найдем знаки производной в получившихся промежутках и изобразим схематично график функции:

$PIC$

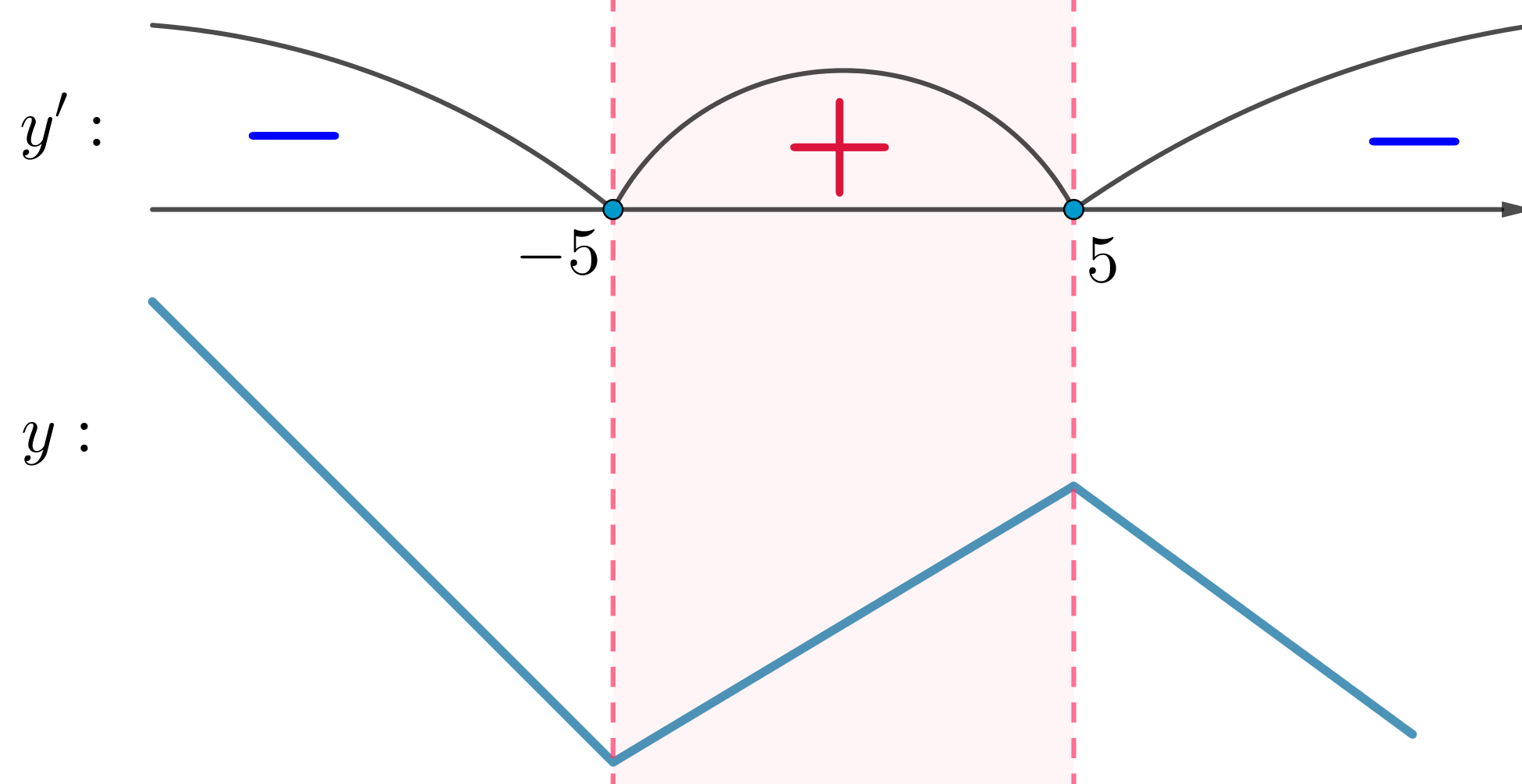
Таким образом, на отрезке $[−5;5]$ функция $y$ возрастает. Следовательно, наименьшее значение на этом отрезке она принимает в точке $x = −5 :$

y(−5)= 13− 5⋅75+ 53 = −237

Ответ: -237

Ошибка.
Попробуйте повторить позже

Задача 2#2742

Найдите наименьшее значение функции $y = 2x2 + 2x + 11$ на отрезке $[− 4;0]$ .

Показать ответ и решение

ОДЗ: $x$ – произвольный.

1)

y′ = 4x + 2

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна $0$ или не существует):

4x + 2 = 0 ⇔ x = − 0,5.

Производная существует при любом $x$ .

2) Найдём промежутки знакопостоянства $′ y$ :

$PIC$

3) Найдём промежутки знакопостоянства $′ y$ на рассматриваемом отрезке $[− 4;0]$ :

$PIC$

4) Эскиз графика на отрезке $[− 4;0]$ :

$PIC$

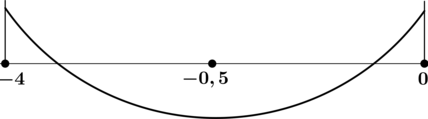
Таким образом, наименьшего на $[− 4;0]$ значения функция достигает в $x = − 0,5$ .

y(− 0,5 ) = 2 ⋅ 0,25 − 1 + 11 = 10,5.

Итого: $10,5$ – наименьшее значение функции $y$ на $[− 4;0]$ .

Ответ: 10,5

Ошибка.
Попробуйте повторить позже

Задача 3#32320

Найдите наибольшее значение функции $y = x3 − 4x2+ 4x$ на отрезке $[−4;−1].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 3x − 8x+ 4

Найдем нули производной:

′ 2 2 y= 0 ⇒ 3x − 8x+ 4= 0 ⇔ x = 3;2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 2;0]$ попадает нуль производной $x =− 1$ .

$PICT$

При $x∈ [− 4;− 1]$ производная положительна, то есть функция возрастает. Следовательно, на отрезке $[−4;−1]$ наибольшее значение достигается в точке $x= −1$ , и оно равно

y(−1)=− 1− 4− 4 =− 9.

Ответ: -9

Ошибка.
Попробуйте повторить позже

Задача 4#32319

Найдите наибольшее значение функции $y = x7 +5x3− 16$ на отрезке $[−9;1].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 6 2 y =7x + 15x

Найдем нули производной:

′ 2 4 2 y = 0 ⇒ x (7x +15)= 0 ⇔ x = 0 ⇔ x= 0

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[−9;1]$ попадает нуль производной $x =0$ .

$PICT$

При $x∈ [− 9;1]$ производная неотрицательна, то есть функция возрастает. Следовательно, на отрезке $[−9;1]$ наибольшее значение достигается в точке $x= 1$ , и оно равно

y(1)= 1+5 − 16= −10.

Ответ: -10

Ошибка.
Попробуйте повторить позже

Задача 5#32318

Найдите наибольшее значение функции $y = x3 − 3x+ 4$ на отрезке $[− 2;0].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 3x − 3

Найдем нули производной:

′ 2 y= 0 ⇒ x = 1 ⇔ x =±1

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 2;0]$ попадает нуль производной $x =− 1$ .

$PICT$

При $x∈ [− 2;− 1)$ производная положительна, то есть функция возрастает; при $x∈ (−1;0]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[−2;0]$ наибольшее значение достигается в точке максимума $x= −1$ , и оно равно

y(− 1)= −1 +3+ 4= 6.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 6#32317

Найдите наибольшее значение функции $y = 3+27x− x3$ на отрезке $[− 3;3].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 27− 3x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[2;10]$ попадает нуль производной $x= 6$ .

$PICT$

При $x∈ [− 3;3]$ производная положительна, то есть функция $y =y(x)$ возрастает. Следовательно, на отрезке $[−3;3]$ наибольшее значение достигается в конце отрезка, то есть в точке $x =3$ , и оно равно

y(3)= 3+ 27⋅3 − 33 = 57.

Ответ: 57

Ошибка.
Попробуйте повторить позже

Задача 7#32316

Найдите наибольшее значение функции $y = 3x5− 20x3− 54$ на отрезке $[−4;− 1].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 4 2 y = 15x − 60x

Найдем нули производной:

′ 2 2 2 y =0 ⇒ 3x(5x − 20)= 0 ⇔ x =0;4 ⇔ x = 0;±2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 4;−1]$ попадает нуль производной $x =− 2$ .

$PICT$

При $x∈ [− 4;− 2)$ производная положительна, то есть функция возрастает; при $x∈ (−2;− 1]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[−4;−1]$ наибольшее значение достигается в точке максимума $x= −2$ , и оно равно

y(− 2)= −3 ⋅25+ 20⋅23− 54= 10.

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 8#32315

Найдите наибольшее значение функции $y = x5 − 5x3− 20x$ на отрезке $[−6;1].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 4 2 y = 5x − 15x − 20

Найдем нули производной:

′ 4 2 2 y = 0 ⇒ 5(x − 3x − 4)= 0 ⇔ x = −1;4 ⇔ x = ±2

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 6;1]$ попадает нуль производной $x =− 2$ .

$PICT$

При $x∈ [− 6;− 2)$ производная положительна, то есть функция возрастает; при $x∈ (−2;1]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[−6;1]$ наибольшее значение достигается в точке максимума $x= −2$ , и оно равно

y(−2)= −25+5 ⋅23+ 20⋅2= 48.

Ответ: 48

Ошибка.
Попробуйте повторить позже

Задача 9#32314

Найдите наибольшее значение функции $y = 15 +12x+ x3$ на отрезке $[−2;2].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y= 12+ 3x

Найдем нули производной:

′ 2 y =0 ⇒ 3(4+ x )= 0 ⇔ x∈ ∅

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. В нашем случае производная таковых точек не имеет, следоваитетно, всюду принимает значения одного знака, а именно $y′(x) >0$ для всех $x ∈ℝ$ (это можно проверить, подставив, например, $x= 0$ ). Следовательно, функция возрастает на всем $ℝ$ , значит, на отрезке $[−2;2]$ наибольшее значение достигается в конце отрезка, то есть в точке $x =2$ , и оно равно

3 y(2)= 15+ 12⋅2+ 2 =47.

Ответ: 47

Ошибка.
Попробуйте повторить позже

Задача 10#32313

Найдите наибольшее значение функции

3 2 y = x − 6,5x + 14x− 14

на отрезке $[−4;3].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ.$ Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

y′ = 3x2− 13x +14

Найдем нули производной:

7 y′ = 0 ⇒ 3x2− 13x+ 14= 0 ⇔ x = 2;3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков.

$PICT$

При $x∈ [− 4;2)$ производная положительна, то есть функция возрастает; при $( 7) x ∈ 2;3$ производная отрицательна, то есть функция убывает; при $( ] x ∈ 73;3$ производная положительна, то есть функция снова возрастает. Следовательно, на отрезке $[−4;3]$ наибольшее значение достигается в точке максимума $x= 2$ или в конце отрезка $x= 3 :$

y(2) =23 − 6,5⋅22+ 14⋅2− 14= − 4 y(3) =33 − 6,5⋅32+ 14⋅3− 14= − 3,5

Следовательно, наибольшее значение функции равно -3,5.

Ответ: -3,5

Ошибка.
Попробуйте повторить позже

Задача 11#32312

Найдите наибольшее значение функции $y = 3x − 2x√x$ на отрезке $[0;4].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную (заметим, что $√ - 32 x x= x$ ):

′ 1 y =3 − 3x2

Найдем нули производной:

′ √- y = 0 ⇒ x = 1 ⇔ x= 1

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x ∈[0;1)$ производная положительна, то есть функция возрастает; при $x∈ (1;4]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[1;4]$ наибольшее значение достигается в точке максимума $x =1$ , и оно равно

y(1)= 3⋅1− 2⋅1 =1.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 12#32311

Найдите наименьшее значение функции $y = x√x− 3x+ 1$ на отрезке $[1;9].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную (заметим, что $√ - 32 x x= x$ ):

′ 3 1 y= 2x 2 − 3

Найдем нули производной:

√- y′ = 0 ⇒ x = 2 ⇔ x= 4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x ∈[1;4)$ производная отрицательна, то есть функция $y = y(x)$ убывает; при $x∈ (4;9]$ производная положительна, то есть функция возрастает. Следовательно, на отрезке $[1;9]$ наименьшее значение достигается в точке $x= 4$ , и оно равно

y(4)= 432 − 3⋅4+ 1= −3.

Ответ: -3

Ошибка.
Попробуйте повторить позже

Задача 13#32310

Найдите наибольшее значение функции $y = 3x − 2x32$ на отрезке $[0;7].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 1 y =3 − 3x2

Найдем нули производной:

′ √- y = 0 ⇒ x = 1 ⇔ x= 1

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x ∈[0;1)$ производная положительна, то есть функция возрастает; при $x∈ (1;7]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[1;9]$ наибольшее значение достигается в точке максимума $x =1$ , и оно равно

y(1)= 3⋅1− 2⋅1 =1.

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 14#32309

Найдите наибольшее значение функции $y = x3 +2x2− 4x+4$ на отрезке $[−2;0].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 3x +4x− 4

Найдем нули производной:

′ 2 2 y = 0 ⇒ 3x + 4x − 4 =0 ⇔ x= −2;3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 2;0]$ попадает нуль производной $x =− 2$ .

$PICT$

При $x∈ [− 2;0]$ производная отриательна, то есть функция убывает. Следовательно, на отрезке $[− 2;0]$ наибольшее значение функции достигается в точке $x= −2$ , и оно равно

y(−2)= −23+2 ⋅22+ 4⋅2+ 4= 12.

Ответ: 12

Ошибка.
Попробуйте повторить позже

Задача 15#32308

Найдите наибольшее значение функции $y = x3 − 6x2$ на отрезке $[− 3;3].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 3x − 12x

Найдем нули производной:

′ y = 0 ⇒ 3x(x − 4)= 0 ⇔ x= 0;4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[−3;3]$ попадает нуль производной $x =0$ .

$PICT$

При $x∈ [− 3;0)$ производная положительна, то есть функция $y = y(x)$ возрастает; при $x ∈(0;3]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[−3;3]$ функция имеет точку максимума $x= 0$ , в которой и достигается наибольшее значение на этом отрезке, и оно равно

y(0)=0.

Ответ: 0

Ошибка.
Попробуйте повторить позже

Задача 16#32307

Найдите наибольшее значение функции $y = x3 − 3x+ 4$ на отрезке $[− 2;0].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 3x − 3

Найдем нули производной:

′ 2 y= 0 ⇒ x = 1 ⇔ x =±1

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков. Из точек, где производная равна нулю или не существует, на отрезок $[− 2;0]$ попадает нуль производной $x =− 1$ .

$PICT$

При $x∈ [− 2;−1)$ производная положительна, то есть функция $y = y(x)$ возрастает; при $x ∈(−1;0]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[−2;0]$ функция имеет точку максимума $x= −1$ , в которой и достигается наибольшее значение на этом отрезке, и оно равно

y(−1)= −13+ 3+4 =6.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 17#32306

Найдите наименьшее значение функции $y = 2x32 − 3x+ 1 3$ на отрезке $[1;9].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 1 y = x2 − 3

Найдем нули производной:

′ √- y = 0 ⇒ x = 3 ⇔ x= 9

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x∈ [1;9]$ производная положительна, то есть функция возрастает. Следовательно, на отрезке $[1;9]$ наименьшее значение достигается в точке $x= 9$ , и оно равно

2 3 y(9)= 3 ⋅92 − 3⋅9+ 1= −8.

Ответ: -8

Ошибка.
Попробуйте повторить позже

Задача 18#32304

Найдите наименьшее значение функции $y = 2x32 − 3x+ 1 3$ на отрезке $[1;9].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 1 y = x2 − 3

Найдем нули производной:

′ √- y = 0 ⇒ x = 3 ⇔ x= 9

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x∈ [1;9]$ производная отрицательна, то есть функция убывает. Следовательно, на отрезке $[1;9]$ наименьшее значение достигается в точке $x= 9$ , и оно равно

2 3 y(9)= 3 ⋅92 − 3⋅9+ 1= −8.

Ответ: -8

Ошибка.
Попробуйте повторить позже

Задача 19#32303

Найдите наименьшее значение функции $y = x32 − 3x+ 1$ на отрезке $[1;9].$

Показать ответ и решение

Функция определена при всех $x ≥0$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 3 1 y= 2x 2 − 3

Найдем нули производной:

√- y′ = 0 ⇒ x = 2 ⇔ x= 4

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x ∈[1;4)$ производная отрицательна, то есть функция $y = y(x)$ убывает; при $x∈ (4;9]$ производная положительна, то есть функция возрастает. Следовательно, на отрезке $[1;9]$ наименьшее значение достигается в точке $x= 4$ , и оно равно

y(4)= 432 − 3⋅4+ 1= −3.

Ответ: -3

Ошибка.
Попробуйте повторить позже

Задача 20#32302

Найдите наибольшее значение функции $y = 5+9x− x3 3$ на отрезке $[−3;3].$

Показать ответ и решение

Функция определена при всех $x ∈ℝ$ . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее производную:

′ 2 y = 9− x

Найдем нули производной:

′ 2 y= 0 ⇒ x = 9 ⇔ x =±3

Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:

$PICT$

При $x∈ [− 3;3]$ производная положительна, то есть функция $y =y(x)$ возрастает. Следовательно, на отрезке $[−3;3]$ наибольшее значение доистигается в точке $x= 3$ , и оно равно

33 y(3)= 5+ 9⋅3− 3-= 23.

Ответ: 23