Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Сделаем замену Тогда имеем:
Следовательно, уравнение равносильно
Так как замена линейная, то исходное уравнение имеет единственное решение тогда и только тогда, когда уравнение с заменой имеет единственное решение.
Функция является четной и уравнение имеет вид
. Следовательно, если это
уравнение имеет решение
, то оно имеет также решение
. Значит, количество решений уравнения будет
четным, если среди решений нет
, и нечетным, если среди решений уравнения есть
. Так как нам
требуется, чтобы уравнение имело единственное решение, что является нечетным количеством, то
— решение
уравнения.
- 1.
- Найдем, при каких
число
является решением уравнения:
- 2.
- Проверим, является ли
единственным корнем уравнения при найденных
или уравнение имеет другие корни. Для этого заметим, что если мы определим хотя бы один корень
, то найденные значения параметра нам не подойдут. Если же мы докажем, что других корней нет, то найденные
нам подходят.
Итак, при
уравнение имеет вид
Следовательно,
нам подходит.
При
уравнение имеет вид
Левая часть уравнения
, а правая часть уравнения
Следовательно, по методу оценки равенство возможно тогда и только тогда, когда обе части равны нулю:
Следовательно,
нам подходит.
При
уравнение имеет вид
Рассмотрим функции
Сравним значения функций в точках
и 1.
Тогда имеем:
Так как функции непрерывны на всей области определения, то существует
при котором
то есть
является корнем уравнения. Следовательно, уравнение имеет как минимум три корня, значит,
нам не подходит.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно два решения.
Рассмотрим первое уравнение. При оно равносильно
Рассмотрим это уравнение как квадратное относительно Дискриминант
равен
Следовательно,
Следовательно, первое уравнение задает на координатной плоскости две
прямые
и
с выколотыми на этих
прямых точками пересечения с прямой
Это точки
и
Неравенство системы задает круг с центром в точке и радиусом
Этот круг при
вырождается в точку
Заметим, что центр
круга движется по прямой
Изобразим графики и те положения круга, при
которых он имеет ровно две общие точки с прямыми.
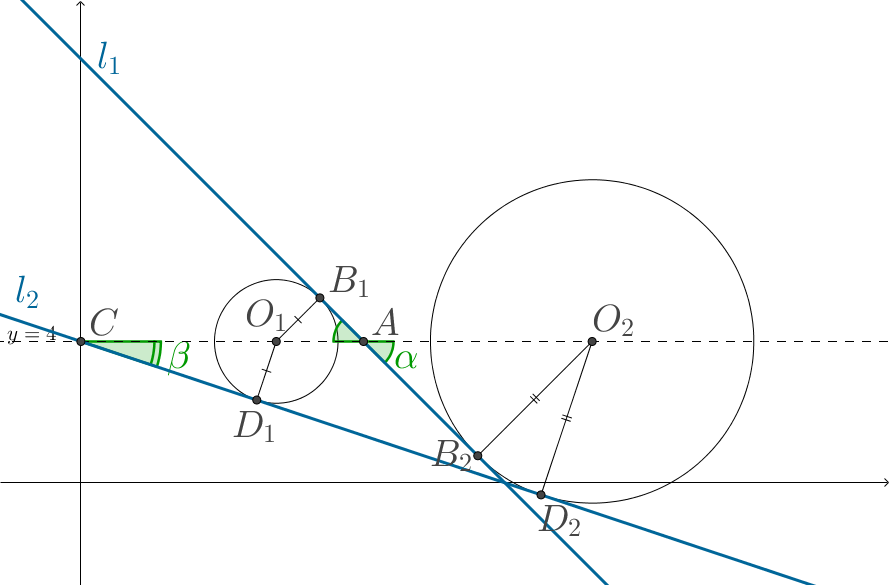
Нам подходят всего два положения круга, определенные положением центра: в
точке и в точке
когда окружность касается обеих прямых одновременно.
При этом точки
и
прямой
не совпадают с точкой
(ординаты
разных знаков) и точки
и
прямой
не совпадают с точкой
(абсциссы разных знаков).
Если окружность пересекает хотя бы одну из прямых в двух точках, то это значит, что все точки этой прямой, лежащие между двумя точками пересечения, являются решением системы. То есть решений будет бесконечно много и этот случай нам не подойдет.
Заметим сразу, что из уравнений прямых определяется угол наклона этих
прямых к оси коэффициент
перед
в уравнении прямой
равен тангенсу угла наклона прямой. Следовательно,
— острый угол
между прямой
и горизонталью;
— острый угол между прямой
и горизонталью.
Выпишем нужные нам точки:
Положение 1: точка
— радиусы окружности, перпендикулярные прямым. Так
как
то можно найти отрезки
и
С другой стороны, длина равна модулю разности абсцисс точек
и
Аналогичные рассуждения для отрезка
Получаем систему:
Положение 2: точка
Имеем:
Таким образом, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы один корень. В ответ укажите наибольшее значение
Уравнение определено при Также стоить заметить, что при
уравнение не имеет решений, так как левая часть
правая
и не
существует такого
при котором они одновременно равны нулю. Следовательно,
Перепишем уравнение в виде
При имеем
Исследуем производную этой функции.
Найдем нули производной:
Производная положительна на всей области определения, следовательно,
— возрастает при всех
Изобразим график функции и график функции
при таком
при котором они пересекаются хотя бы в одной точке.
Такое положение параболы задается следующим условием:
откуда
Следовательно, наибольшее
равно 2.
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых уравнение
имеет ровно три различных корня.
Источники:
Пусть
Тогда уравнение имеет вид
и
равносильно
Заметим, что Следовательно, в буквах
и
уравнение
равносильно
Вернувшись полностью к переменной получаем. что исходное уравнение
равносильно
Полученная совокупность, а значит и исходное уравнение, может иметь максимум 3 корня. Это выполняется, если каждый корень удовлетворяет своему неравенству и корни попарно не равны друг другу:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно один корень на отрезке
Источники:
Так как уравнение вида равносильно
то наше уравнение
равносильно
Назовем число хорошим, если оно удовлетворяет условию и лежит в
отрезке
в противном случае будем называть число плохим. Определим, при
каких
числа
и
хорошие и плохие.
— хорошее, если
Тогда — плохое, если
— хорошее, если
Тогда — плохое, если
Нам подходят ситуации, когда ровно одно из чисел хорошее (а второе, соответственно, плохое) либо когда оба числа равны и хорошие.
хор-плох:
плох-хор:
хор-хор и равны:
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых неравенство
имеет решения.
Так как для любого имеем
то
Следовательно, основание
логарифмов может быть разве что от 0 до 1. Следовательно, неравенство
равносильно
Графиком последних двух неравенств является верхний полукруг с центром
радиуса 1 без нижней границы. Необходимо, чтобы объединение двух
полос, заданных первыми тремя неравенствами, имело с этим полукругом хотя бы
одно пересечение. Определим
при которых наоборот: решений нет.
Пусть — прямая вида
касающаяся полукруга,
—
прямая вида
проходящая через точку
Рассмотрим первый случай: когда нижняя границы полосы находится
совпадает с или находится выше. Тогда, во-первых, прямая поднята вверх
относительно начального положения
следовательно,
Во-вторых, расстояние от центра полукруга до прямой
больше радиуса
полукруга. Следовательно, эти положения задаются следующей системой:
Рассмотрим второй случай: когда верхняя граница полосы совпадает с или
находится ниже. Это задается неравенством
Следовательно, итоговый ответ:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы одно решение.
Так как то уравнение равносильно
При уравнение равносильно
следовательно, решением
уравнения будут
Значит,
нам подходит.
Пусть далее Тогда уравнение равносильно
Так как то полученное уравнение имеет решения, если
Следовательно, итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет или семь, или восемь различных решений.
Перепишем уравнение в виде
Пусть Так как
— функция, то разным
значениям
обязательно соответствуют разные значения
Тогда уравнение
примет вид
Исследуем новую переменную:
при
уравнение
не имеет решений.
при
имеем
и
Следовательно,
при имеем
— два решения;
при имеем
— три решения;
при имеем
— четыре решения.
при
имеем
— два решения.
Следовательно, необходимо, чтобы уравнение
имело два корня
или
Найдем дискриминант нашего уравнения:
Нужно, чтобы то есть
При этом рассмотрим два случая:
- 1.
Тогда
Этот случай нам подходит.
- 2.
Тогда парабола
должна выглядеть следующим образом:
Следовательно, такая парабола задается системой
Значит, итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых множество решений
неравенства
является отрезком длиной 1.
Неравенство равносильно
Сделаем замену Тогда для новой переменной сохраняется то же
условие, что и для старой. Неравенство равносильно
Рассмотрим последнюю систему. Ее решением должно быть множество, которое
в объединении с точкой образует отрезок длины 1. Рассмотрим
неравенство
Решим его графически в системе координат Левая часть
представляет собой верхнюю полуокружность с центром в точке
радиуса 1.
Правая часть
представляет собой пучок прямых, проходящих через
точку
Изобразим положения, при которых выполняется условие задачи:
Все положения прямой между изображенным положением и вертикалью нам
подходят. Изображенное положение — когда прямая проходит через точку
Следовательно, итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно два различных решения.
Пусть Исследуем новую переменную. Если
то уравнение
не имеет решений, так как
следовательно,
При
это
уравнение имеет единственный корень
при
оно имеет два
решения.
Рассмотрим исходное уравнение после этой замены. При оно
равносильно
Это уравнение квадратное. Найдем его дискриминант:
Чтобы выполнялось условие задачи, нужно, чтобы один корень был больше 1, а второй либо не существовал, либо был меньше 1.
- 1.
Тогда единственный корень уравнения
При
имеем
— подходит. При
имеем
— не подходит.
- 2.
или
(при
). Тогда парабола
должна задаваться одним из следующих способов:
Эти графики и положения точки 1 задаются следующими условиями:
Следовательно, итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых участок графика
функции
при
находится строго выше аналогичного
участка графика функции
Условие задачи равносильно следующему условию: найти при которых
неравенство
верно при всех
Следаем замену Тогда неравенство равносильно
Получили квадратичное неравенство, решение которого зависит от
того, где расположено число на вещественной прямой. Рассмотрим
случаи:
- 1.
Тогда неравенство равносильно
Множество
не содержит в себе интервал
следовательно, этот случай нам не подходит.
- 2.
Тогда неравенство равносильно
Множество
содержит интервал
если
Следовательно, в этом случае нам подходят
- 3.
Тогда неравенство примет вид
Множество
содержит интервал
при всех
Итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно два различных решения
Сделаем замену Тогда уравнение примет вид
Если это уравнение имеет корни, то по теореме Виета сумма и произведение этих корней равны
Нам подходят числа
Следовательно, получаем, что исходное уравнение равносильно
Эти уравнения линейные при и квадратные при
Следовательно,
рассмотрим два случая.
- 1.
Тогда совокупность равносильна
Она имеет два решения. Следовательно,
нам подходит.
- 2.
Рассмотрим дискриминанты первого и второго уравнений соответственно:
Рассмотрим по отдельности некоторые случаи в зависимости от того, равен нулю, меньше или больше нуля каждый дискриминант.
- 2.1.
Следовательно, совокупность имеет два решения. Это нам подходит.
- 2.2.
Тогда каждое уравнение имеет по одному корню. Но эти корни совпадают и равны
следовательно, это значение параметра нам не подходит.
- 2.3.
Этот случай нам может подходить только тогда, когда множества корней первого и второго уравнений совпадают. Это выполнено, если уравнения одинаковы, то есть если
Нам подходит только
Итоговый ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение или не имеет решений.
Пусть Тогда уравнение примет вид
Рассмотрим и исследуем две функции:
Графиком функции является парабола, ветви которой направлены
вверх, а вершина находится в точке
Следовательно,
является
точкой минимума и наименьшее значение функции
равно
Тогда график функции выглядит следующим образом. При этом
заметим, что он при всех
находится в верхней полуплоскости, а
также в силу четности функции
симметричен относительно оси
Функция также четная. Ее графиком является корыто, правая ветвь
которого задается уравнением
дно корыта протяженностью от
до
и высотой
Следовательно,
Тогда получаем график, который при всех находится в верхней
полуплоскости и симметричен относительно оси
Единственное решение уравнение будет иметь, если
В
свою очередь, уравнение не имеет решений при
если при этом правая
ветвь графика функции
не пересекается с правой ветвью графика функции
Проверим, действительно ли при найденных значениях правая ветвь
графика функции
не пересекается с правой ветвью графика функции
Если то графики обеих функций выглядят так:
Тогда исходное уравнение имеет три решения и принимает вид
Следовательно, нам не подходит.
При правая ветвь корыта имеет уравнение
при
и
действительно выполнено
Последнее неравенство выаполняется, так как имеют место оценки
Следовательно, при
и
Значит, правая ветвь
параболы выше правой ветви корыта, а в силу симметрии обоих графиков
относительно оси
и левая ветвь параболы выше левой ветви корыта. То есть
при
графики выглядят следующим образом:
Тогда исходное уравнение имеет единственное решение или не имеет решений при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получено
множество значений | 3 |
| С
помощью верного рассуждения получены
все граничные точки искомого множества
значений | 2 |
| Верно получена хотя бы одна граничная
точка искомого множества значений | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |



