а) Так как и — вписанные, то суммы противоположных углов для каждого четырехугольника равны Тогда и откуда Эти углы являются соответственными при и и секущей Следовательно,

Также и следовательно, Эти углы также являются соответственными при и и секущей следовательно, Тогда Следовательно, — либо трапеция, либо прямоугольник. Но так как косинус одного из углов ненулевой (что не выполнено для углов ), то — трапеция.

Также так как эти углы смежные. Отсюда и из вышезаписанного равенства следует, что Но следовательно, следовательно, трапеция равнобедренная. Чтд.

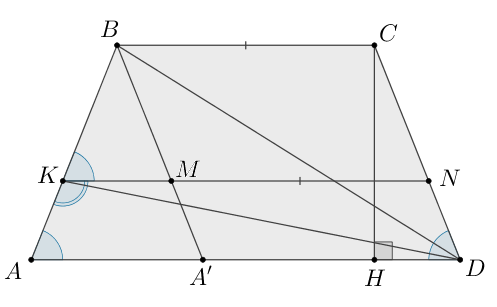
б) Пусть Проведем Тогда

По свойству равнобедренной трапеции

Проведем Пусть Тогда — параллелограмм, следовательно, Тогда

( — общий), следовательно,

Следовательно,

Проведем Тогда окружность, описанная около есть окружность, описанная около Следовательно, по теореме синусов

По теореме косинусов для

Тогда

Проведем Тогда по теореме косинусов для

Если — радиус окружности, описанной около то, так как эта же окружность является описанной около имеем по теореме синусов следующее: