Ошибка.
Попробуйте повторить позже
В прямоугольный треугольник с прямым углом
вписана окружность с
центром в точке
и радиусом
К этой окружности параллельно прямой
проведена касательная, которая пересекает стороны
и
в точках
и
соответственно. В треугольник
вписана окружность с центром в
точке
и радиусом
Прямые
и
пересекаются в точке
а) Докажите, что
б) Найдите площадь треугольника если
Источник:
а) Пусть Так как
— биссектриса угла
то по свойству
биссектрисы
Что и требовалось доказать.
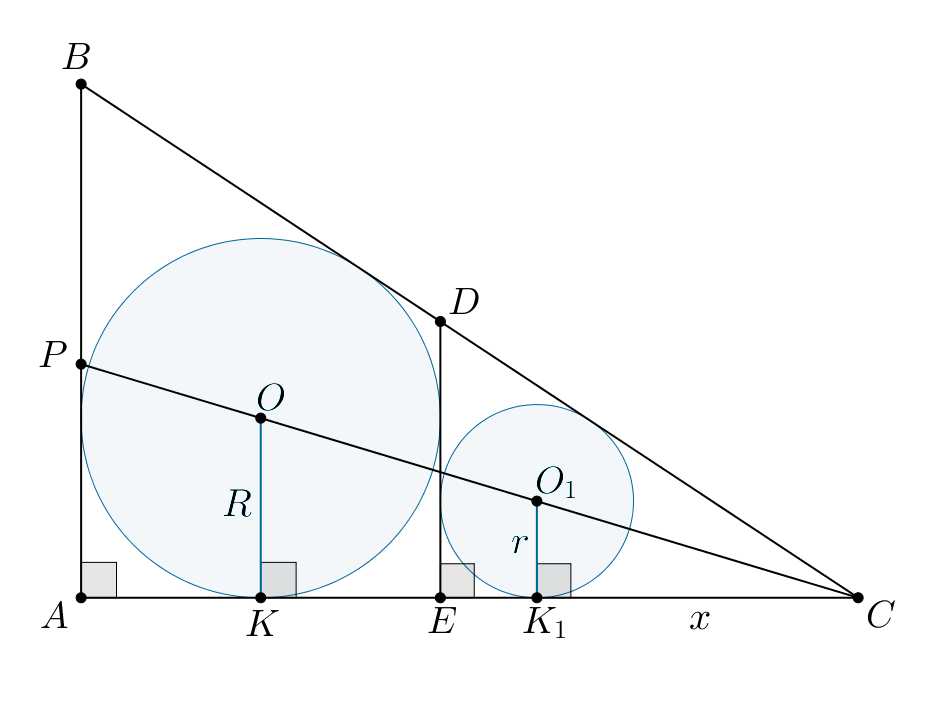
б) Проведем радиусы и
в точки касания окружностей со
стороной
Большая окружность вписана в прямоугольную трапецию
следовательно, ее радиус
равен
Меньшая окружность
вписана в прямоугольный
следовательно, ее радиус
равен
как прямоугольные с общим острым углом. Следовательно,
если
то
Следовательно,
С другой стороны,
При этом Следовательно,
Тогда искомая площадь равна
б) 270
Ошибка.
Попробуйте повторить позже
В трапеции с основаниями
и
провели биссектрисы углов
и
которые пересекаются в точке
Через точку
параллельно
прямой
провели прямую, которая пересекает стороны
и
соответственно в точках
и
При этом
а) Докажите, что трапеция равнобедренная.
б) Найдите если
Источник:
а)
как накрест лежащие, следовательно,
и
— равнобедренные, откуда
Так как то из
следует, что
По
теореме Фалеса
Следовательно,
Значит, трапеция равнобедренная. Что и требовалось доказать.
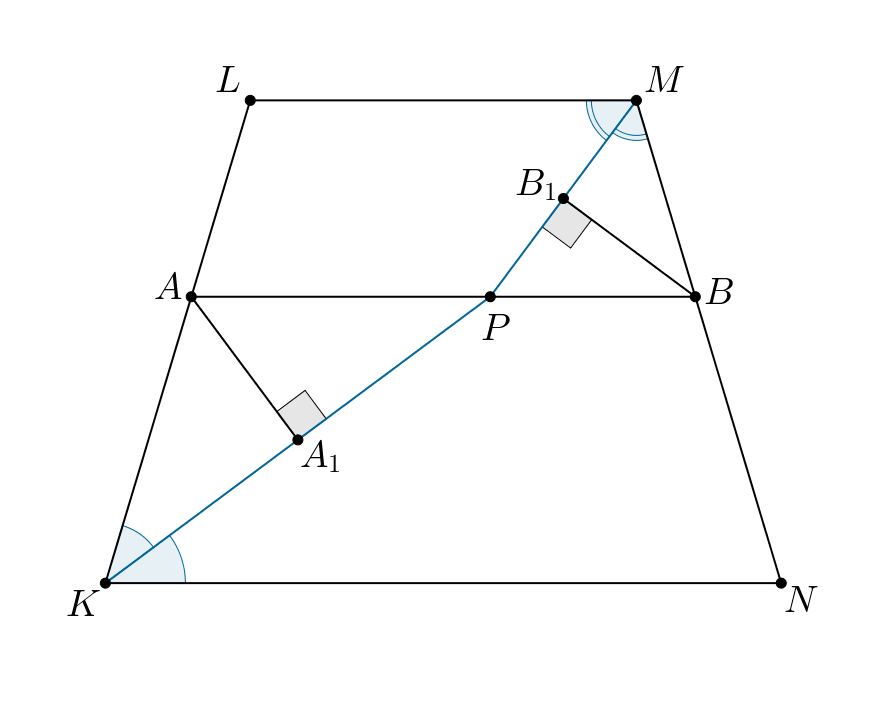
б) Проведем
Обозначим
Так
как трапеция равнобедренная, то
откуда
Тогда
как прямоугольные с равными острыми углами.
Следовательно,
Тогда
Тогда
б) 0,28
Ошибка.
Попробуйте повторить позже
На стороне ромба
отметили точку
так, что
Через точку
перпендикулярно
провели прямую, которая пересекает
диагонали
и
в точках
и
соответственно, при этом
а) Докажите, что точка делит отрезок
в отношении
считая от
вершины
б) Найдите периметр ромба если
Источник:
а) Пусть прямая пересекает сторону
в точке
как
прямоугольные по острому углу (
как вертикальные).
Следовательно,
Следовательно, если то
Тогда
и
по тому же признаку, следовательно,
Что и требовалось доказать.

б) Пусть
Тогда
Тогда Следовательно,
Так как то
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В равнобедренной трапеции боковая сторона
равна
а основание
больше основания
Построена окружность, касающаяся сторон
и
а) Докажите, что если то окружность пересекает сторону
в
двух точках.
б) Найдите длину той части отрезка которая находится внутри
окружности, если
Источник:
а) Пусть
— трапеция, описанная около данной окружности.
Пусть
Тогда суммы противоположных сторон трапеции
равны, следовательно,
То, что окружность пересекает в двух точках, равносильно тому, что
Если окружность не пересекает сторону
или касается ее, то
имеем:
Получили противоречие. Следовательно, окружность пересекает сторону в
двух точках. Что и требовалось доказать.
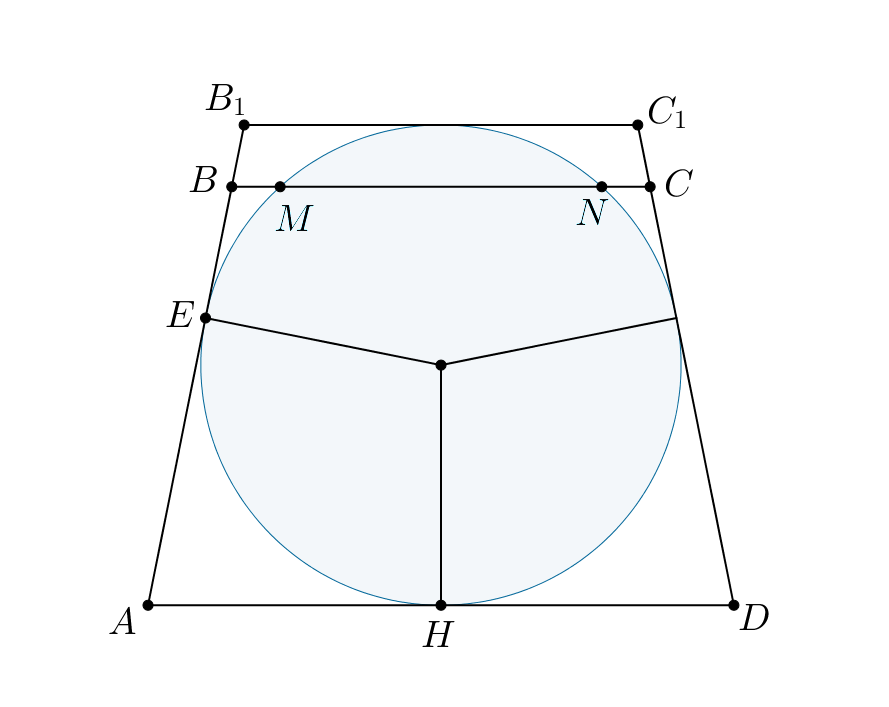
б) Пусть окружность пересекает в точках
и
считая от точки
Пусть
Тогда
Так как трапеция равнобедренная, то точка
касания окружности с основанием
делит его пополам. Следовательно,
Так как отрезки касательных равны, то для точки
касания
окружности со стороной
имеем:
Так как квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то
б)
Ошибка.
Попробуйте повторить позже
В параллелограмме угол
вдвое больше угла
Биссектриса
угла
пересекает отрезок
в точке
На продолжении стороны
за
точку
выбрана такая точка
что
а) Докажите, что
б) Найдите если
Источник:
а) Пусть Тогда
Так как
как накрест лежащие при
и секущей
а
— общий у
и
то эти треугольники подобны по двум
углам. Следовательно,
Что и требовалось доказать.
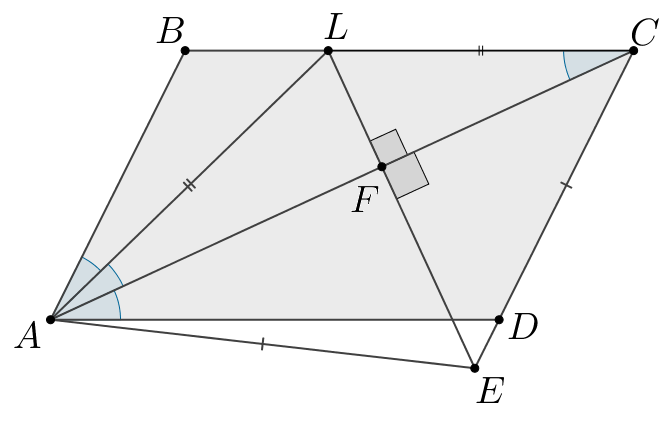
б) по трем сторонам (
равнобедренный, так как углы
при стороне
равны
). Следовательно, если
то
и
— биссектрисы равнобедренных треугольников
и
проведенные к
основанию
Тогда они также являются высотами и медианами, следовательно,
По условию следовательно,
Найдем
Следовательно,
Тогда искомый отрезок равен
б) 14,2
Ошибка.
Попробуйте повторить позже
В параллелограмме угол
вдвое больше угла
Биссектриса
угла
пересекает отрезок
в точке
На продолжении стороны
за
точку
выбрана такая точка
что
а) Докажите, что
б) Найдите если
Источник:
а) Пусть
и
Тогда нужно доказать, что
Тогда как накрест лежащие при
и секущей
1 способ
Треугольники и
подобны по двум углам, так как
общий и
Запишем отношение подобия:
Что и требовалось доказать.
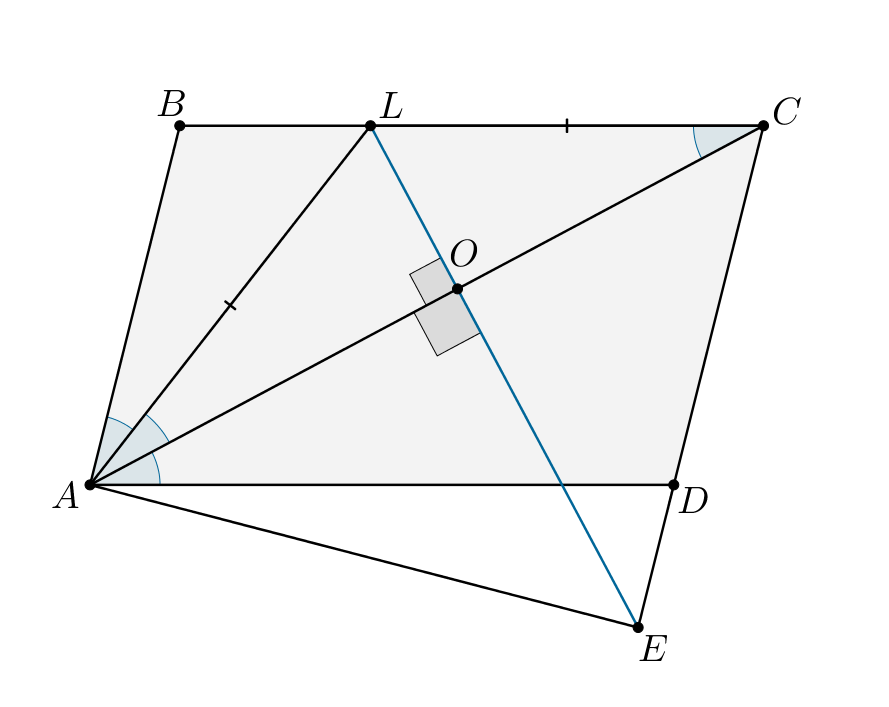
2 способ
Так как то
равнобедренный, значит,
Далее,
как односторонние углы при
и секущей
Следовательно,
Тогда получаем следующие
соотношения:
Что и требовалось доказать.
б) По пункту а) по условию
следовательно,
треугольники
и
равны по трем сторонам (
— общая).
Отсюда
и
— биссектриса, а значит, медиана и высота в
равнобедренном треугольнике
Аналогично
— биссектриса, медиана и
высота в равнобедренном треугольнике
Далее, из условия следует
В прямоугольном имеем:
В прямоугольном имеем:
Тогда искомый отрезок равен
б) 29,7
Ошибка.
Попробуйте повторить позже
Четырехугольник со сторонами
и
вписан в
окружность радиусом
а) Докажите, что прямые и
параллельны.
б) Найдите
Источник:
а) Проведем и рассмотрим
и
Так как равные хорды
стягивают равные меньшие дуги, то меньшие дуги
и
равны,
следовательно,
как вписанные углы, опирающиеся на эти дуги.
Это накрест лежащие углы при параллельных прямых
и
и
секущей
Следовательно,
Что и требовалось доказать.

б) По теореме синусов для
Проведем Тогда
то есть
Далее имеем:
Тогда из прямоугольного по теореме Пифагора
Следовательно, Значит,
Тогда
Замечание.
Четырехугольник не является прямоугольником, поскольку в таком
случае для прямоугольного треугольника
имели бы
и
что неверно.
б) 32
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Четырехугольник со сторонами
и
вписан в
окружность радиусом
а) Докажите, что прямые и
параллельны.
б) Найдите
Источник:
а) Углы как вписанные, которые опираются на равные дуги,
стягиваемые равными отрезками
и
Также эти углы являются накрест
лежащими при прямых
и
и секущей
Таким образом,
Что и требовалось доказать.
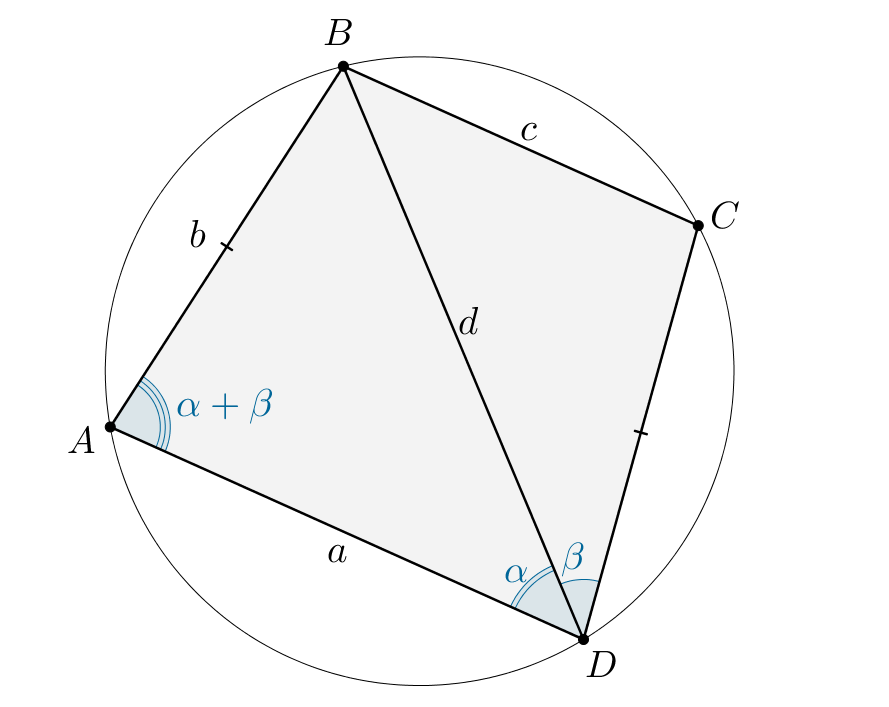
б) Из пункта а) следует, что по двум сторонам и углу
между ними, так как
— общая,
(как вписанные,
опирающиеся на равные дуги). Отсюда получаем
Обозначим
тогда по теореме Птолемея
имеем:
Найдем
Пусть Рассмотрим
Он вписан в ту
же окружность, что и четырехугольник
Следовательно, по теореме
синусов
Тогда, так как получаем
По теореме синусов в
Тогда
б) 42,16
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В трапеции с меньшим основанием
точки
и
— середины
сторон
и
соотвественно. В каждый из четырехугольников
и
можно вписать окружность.
а) Докажите, что трапеция равнобедренная.
б) Найдите радиус окружности, описанной около трапеции если
а радиус окружности, вписанной в четырехугольник
равен
Источник:
а) Если четырехугольник описанный, то суммы противоположных сторон этого четырехугольника равны. Следовательно,
Что и требовалось доказать.
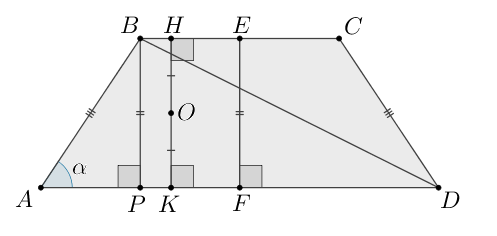
б) Пусть — центр окружности, вписанной в
Тогда
и
— радиусы этой окружности. Так как
то
точки
лежат на одной прямой, следовательно,
— высота трапеции
равная
В равнобедренной трапеции отрезок, соединяющий середины оснований,
перпендикулярен основаниям, следовательно, и
Так
как
— описанный, то суммы противоположных сторон равны, значит, если
то
Следовательно, и тогда
Так как — вписанная трапеция, то ее площадь можно найти по
формуле (
— полупериметр)
Так как то
Из находим, что
следовательно,
Следовательно, В силу симметрии решаемой системы
относительно перемены местами и
если принять, что
получаем
Пусть Тогда по свойству равнобедренной трапеции
Следовательно,
Тогда по теореме
Пифагора
Если
то
следовательно, по теореме
синусов
Так как окружность, описанная около это та же окружность, что
описана около
то мы нашли ее радиус и он равен
б) 9,1
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В трапеции с меньшим основанием
точки
и
— середины
сторон
и
соответственно. В каждый из четырехугольников
и
можно вписать окружность.
а) Докажите, что трапеция равнобедренная.
б) Найдите радиус окружности, описанной около трапеции если
а радиус окружности, вписанной в четырехугольник
равен
7.
Источник:
а) Пусть Если в четырехугольник вписана
окружность, то суммы противоположных сторон равны. Следовательно,
Что и требовалось доказать.
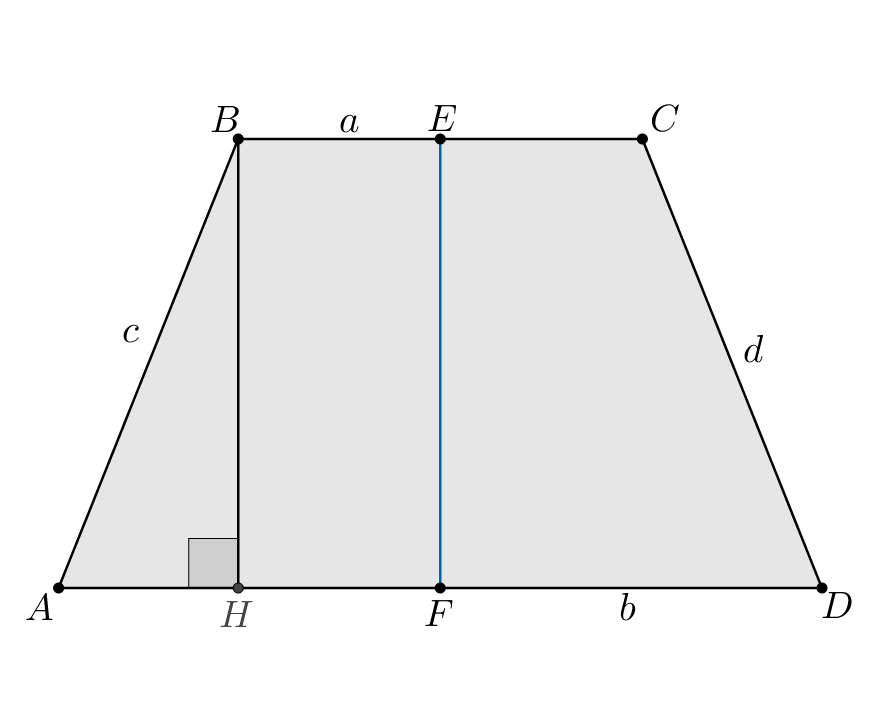
б) Высота трапеции равна диаметру окружности, вписанной в эту трапецию.
Проведем Тогда имеем:
Так как при этом то
— параллелограмм и
Тогда
Пусть полупериметр трапеции равен
Тогда по формуле
Брахмагупты квадрат площади этой трапеции равен
С другой стороны, площадь этой трапеции равна
Отсюда получаем уравнение

Из пункта а) следует, что
Подставим это в уравнение выше и получим
Обозначим и проведем
Тогда окружность, описанная
около
есть окружность, описанная около
По теореме синусов
для этого треугольника
Найдем В прямоугольном треугольнике
имеем:
Также имеем:
Тогда по теореме Пифагора из
Тогда искомый радиус равен
б)
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке касается гипотенузы
прямоугольного
треугольника
и пересекает его катеты
и
в точках
и
Точка
— основание высоты, опущенной из вершины
и
— центры
окружностей, вписанных в треугольники
и
а) Докажите, что и
лежат на отрезке
б) Найдите расстояние от точки до прямой
если
Источник:
а) Пусть окружность с центром в точке пересекает
в точке
в
точке
Так как эта окружность касается
то радиус, проведенный в точку
касания, перпендикулярен
следовательно,
— радиус этой
окружности. Также
Следовательно,
равнобедренный и
прямоугольный, значит,
Докажем, что лежит на
Для точки
доказательство будет
аналогично.
Пусть — биссектриса
Докажем, что
Рассмотрим
и
Они равны по двум сторонам и углу между
ними (
— общая). Следовательно,
Следовательно, так как
то
следовательно,
— биссектриса второго угла
треугольника
Значит,
— точка пересечения биссектрис
треугольника
значит, это центр вписанной в этот треугольник окружности,
следовательно,
Чтд.
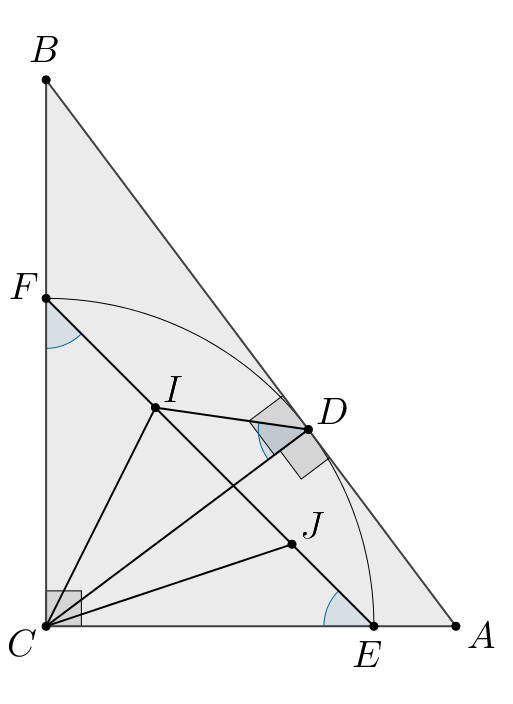
б) Расстояние от точки до прямой
равно высоте
равнобедренного
прямоугольного
проведенной к гипотенузе
А эта высота в свою
очередь равна
Так как то
б)
Ошибка.
Попробуйте повторить позже
На сторонах и
четырехугольника
около которого можно
описать окружность, отмечены точки
и
соответственно. Около
четырехугольников
и
также можно описать окружность.
Косинус одного из углов четырехугольника
равен
а) Докажите, что четырехугольник является равнобедренной
трапецией.
б) Найдите радиус окружности, описанной около четырехугольника
если радиус окружности, описанной около четырехугольника
равен
а
и
Источник:
а) Так как
и
— вписанные, то суммы противоположных
углов для каждого четырехугольника равны
Тогда
и
откуда
Эти углы являются
соответственными при
и
и секущей
Следовательно,
Также и
следовательно,
Эти углы также являются соответственными при
и
и секущей
следовательно,
Тогда
Следовательно,
— либо трапеция, либо прямоугольник. Но так как косинус одного из
углов
ненулевой (что не выполнено для углов
), то
—
трапеция.
Также так как эти углы смежные. Отсюда
и из вышезаписанного равенства
следует, что
Но
следовательно,
следовательно, трапеция равнобедренная. Чтд.
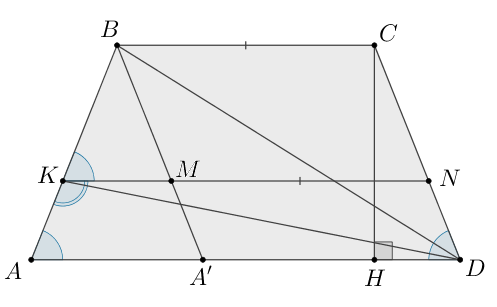
б) Пусть
Проведем
Тогда
По свойству равнобедренной трапеции
Проведем Пусть
Тогда
— параллелограмм,
следовательно,
Тогда
(
— общий), следовательно,
Следовательно,
Проведем Тогда окружность, описанная около
есть окружность,
описанная около
Следовательно, по теореме синусов

По теореме косинусов для
Тогда
Проведем Тогда по теореме косинусов для
Если — радиус окружности, описанной около
то, так как эта же
окружность является описанной около
имеем по теореме синусов
следующее:
б)
Ошибка.
Попробуйте повторить позже
Точки
и
лежат на окружности в указанном порядке, причем
а прямые
и
перпендикулярны. Отрезки
и
пересекаются в точке
а) Докажите, что прямая пересекает отрезок
в его середине.
б) Найдите площадь треугольника если
Источник:
а) Меньшие дуги, стягиваемые равными хордами, равны, следовательно, равны
меньшие дуги
и
Вписанные углы, опирающиемся на равные дуги,
равны, следовательно,
Тогда при секущей
и накрест лежащих углах
Следовательно,
Тогда
— диаметр, так как
вписанный

Следовательно, и
как прямоугольные по
общей гипотенузе и острому углу (
как вписанные и
опирающиеся на равные дуги). Отсюда
следовательно,
—
биссектриса в равнобедренном
проведенная к основанию. Значит,
— высота.
Таким образом, — высота и биссектриса в
следовательно, он
равнобедренный и
также является и медианой. Значит,
Что и
требовалось доказать.
б) Пусть Тогда из
имеем:
Следовательно,
Так как — высота и биссектриса, то
равнобедренный и
—
медиана. Следовательно,
Также имеем:
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точки и
лежат на окружности в указанном порядке, причем
а
Точка
— пересечение прямых
и
а) Докажите, что прямая делит отрезок
пополам.
б) Найдите площадь треугольника если
Источник:
а) Так как и
— вписанный четырехугольник, то
—
равнобедренная трапеция. Следовательно,
Углы как вписанные, опирающиеся на равные дуги.
Следовательно, так как
то
— равнобедренный. Отсюда
следует, что
— середина
значит,
также равнобедренный, то есть
Тогда следовательно,
Так как эти углы
являются соответственными при прямых
и
и секущей
то
Тогда
— ромб, следовательно,
— середина диагонали
Что и требовалось доказать.

б) Так как и
делит
пополам, то
— диаметр.
Следовательно,
Так как угол
опирается на дугу в два раза
большую, чем дуга, на которую опирается угол
то
и далее
имеем:
По теореме косинусов из
Заметим, что по двум углам, следовательно,
Тогда окончательно имеем:
б)
Ошибка.
Попробуйте повторить позже
В параллелограмме угол
острый. На продолжениях сторон
и
за точку
выбраны точки
и
соответственно, причем
и
а) Докажите, что
б) Найдите если
Источник:
а) Заметим, что по построению и
— равнобедренные трапеции,
следовательно, диагонали каждой трапеции равны. Тогда у трапеции
равны
и
у трапеции
равны
и
Следовательно,
Что и требовалось доказать.
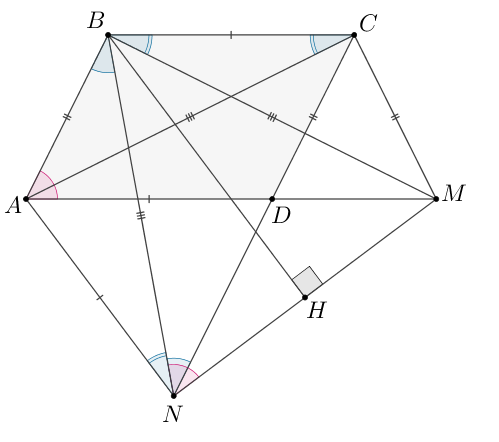
б) Так как и
— равнобедренные трапеции, следовательно,
Обозначим
Тогда
Заметим, что
— равнобедренный, причем
Следовательно, Проведем высоту
Тогда
также является и медианой. Из прямоугольного треугольника
имеем:
Таким образом,
б)
Ошибка.
Попробуйте повторить позже
В параллелограмме тангенс угла
равен
На продолжениях сторон
и
параллелограмма за точку
выбраны точки
и
соответственно, причем
и
а) Докажите, что
б) Найдите если
Источник:
а) Так как — параллелограмм, то
Из условия следует, что
и
равнобедренные, тогда
Аналогично
Тогда
по двум сторонам и углу между ними, откуда
следует, что
Что и требовалось доказать.
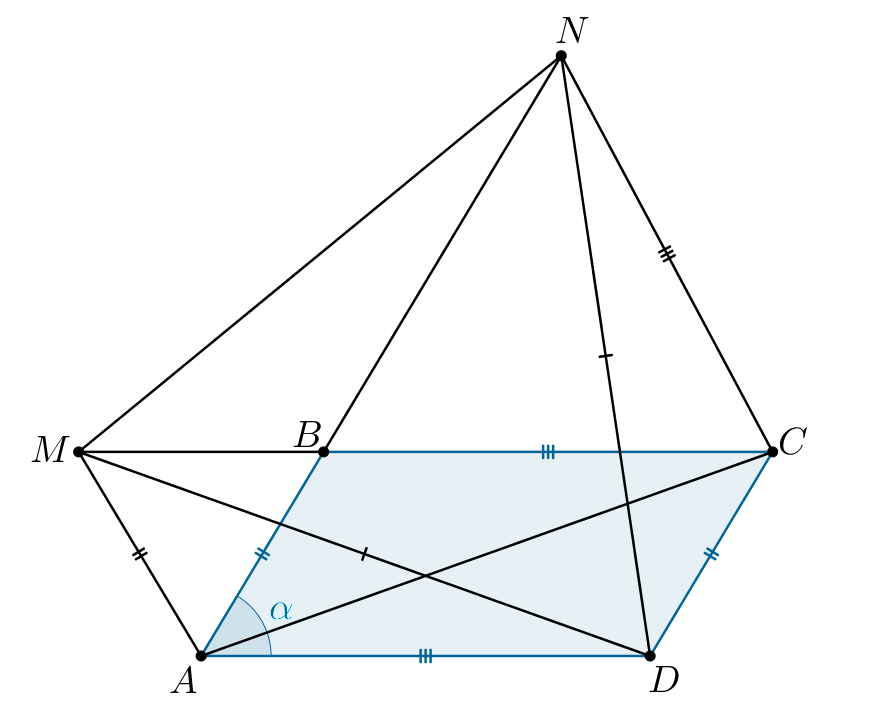
б) Так как
то
Следовательно,
Тогда по теореме косинусов из
б) 4
Ошибка.
Попробуйте повторить позже
Около окружности с центром описана трапеция
с основаниями
и
а) Докажите, что
б) Найдите отношение большего основания трапеции к меньшему, если известно,
что а площадь четырехугольника с вершинами в точках касания
окружности со сторонами трапеции составляет
площади трапеции
Источник:
а) Центр вписанной окружности лежит на пересечении биссектрис углов трапеции.
Так как то
Следовательно,
Аналогично доказывается, что Чтд.
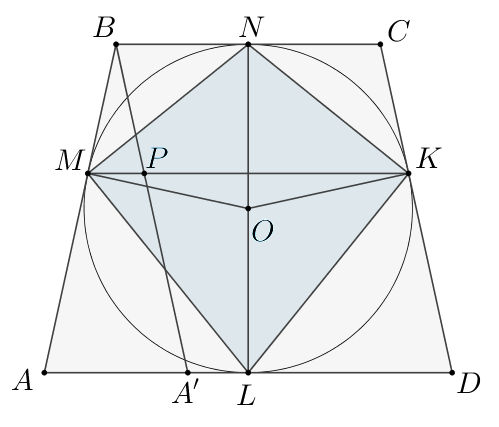
б) Пусть — точки касания окружности со сторонами
и
соответственно. Так как трапеция равнобедренная, то
следовательно,
следовательно,
равнобедренный и
также является и медианой. Тогда
— середина
Аналогично доказывается,
что
— середина
Пусть
Тогда
как
отрезки касательных. Следовательно,
значит,
Также заметим, что лежат на одной прямой, то есть
—
высота трапеции и одна из диагоналей четырехугольника
Так как а
то
Тогда

Найдем Проведем
Тогда
— параллелограмм, а
также
— параллелограмм, где
Следовательно,
следовательно,
Следовательно,
Площадь трапеции равна
Тогда получаем следующее равенство:
Отсюда или
Так как
то
б) 6
Ошибка.
Попробуйте повторить позже
Точки
— середины сторон соответственно
и
остроугольного треугольника
а) Докажите, что окружности, описанные около треугольников
и
пересекаются в одной точке.
б) Известно, что и
Найдите радиус окружности,
вписанной в треугольник, вершины которого — центры окружностей, описанных
около треугольников
и
Источник:
а) Пусть — вторая точка пересечения окружностей, описанных около
треугольников
и
Четырехугольник вписан в окружность, поэтому
Аналогично четырехугольник вписан в окружность, следовательно,
Следовательно,
Следовательно, четырехугольник также вписан в окружность, то
есть точка
лежит на окружности, описанной около треугольника
Чтд.
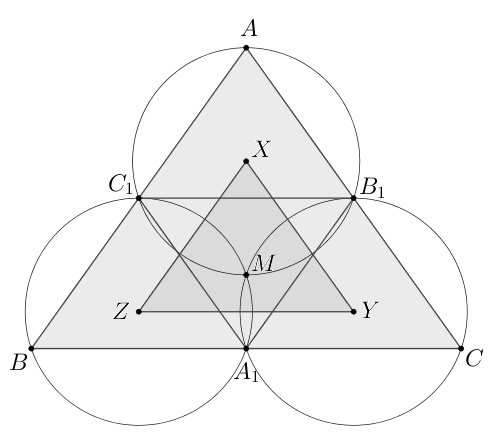
б) Докажем, что
и
— диаметры трех окружностей.
Пусть
— центр окружности, описанной около
Докажем, что
Так как — точка пересечения серединных перпендикуляров к сторонам
то
Отсюда
— вписанный,
следовательно,
лежит на окружности, описанной около
Аналогично доказывается, что
лежит на двух других окружностях,
следовательно,
— точка пересечения всех трех окружностей, то есть это и есть
точка
Из того, что
следует, что
и
— диаметры трех окружностей.
Следовательно, если
и
— центры этих окружностей, то эти точки —
середины отрезков
и
соответственно, значит,
и
— средние линии в
и
соответственно.
Следовательно, стороны
равны половинам сторон
значит, эти
треугольники подобны с коэффициентом подобия
Тогда радиус окружности,
впписанной в
в два раза меньше радиуса окружности, вписанной в
По формуле
радиус окружности, вписанной в
равен
б)
Ошибка.
Попробуйте повторить позже
В трапеции основание
в два раза меньше основания
Внутри
трапеции взяли точку
так, что углы
и
прямые.
а) Докажите, что
б) Найдите если
а расстояние от точки
до прямой
равно стороне
Источник:
а) Продлим боковые стороны и
трапеции до пересечения в точке
Получим
Поскольку как соответственные при
и секущей
а
— общий, то
Так как
то стороны
в 2 раза меньше соответствующих сторон
Следовательно, точка — середина
точка
— середина
Тогда
и
— серединные перпендикуляры к сторонам
и
соответственно.
Так как точка пересечения серединных перпендикуляров к сторонам
треугольника — центр описанной окружности, то — центр описанной около
окружности. Значит,
и
— радиусы этой окружности,
следовательно,
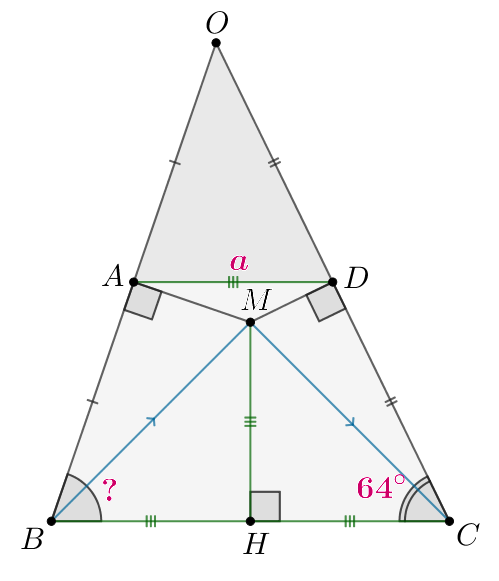
б) Пусть Если
— расстояние от точки
до стороны
то
— серединный перпендикуляр к
В наших обозначениях
Тогда из
по теореме Пифагора
По теореме синусов для
Выбираем так как в противном случае сумма углов
будет
больше
Тогда искомый угол равен
б)
Ошибка.
Попробуйте повторить позже
Точка лежит на отрезке
Прямая, проходящая через точку
касается
окружности с диаметром
в точке
и второй раз пересекает окружность с
диаметром
в точке
Продолжение отрезка
пересекает окружность с
диаметром
в точке
а) Докажите, что прямые и
параллельны.
б) Найдите площадь треугольника если
и
Источник:
а) как вписанные углы, опирающиеся на диаметры
и
окружностей.
как вертикальные углы.
Следовательно,
Эти углы являются накрест
лежащими при
и
и секущей
Следовательно,
Чтд.
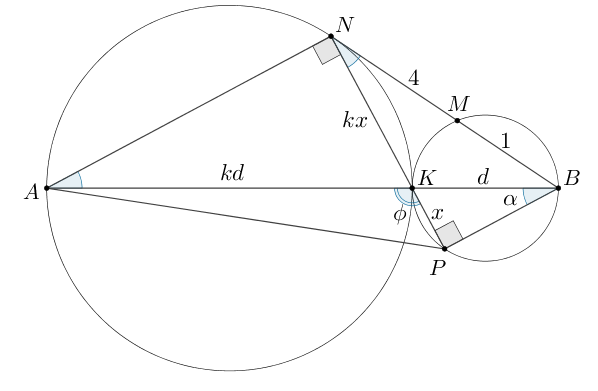
б) как прямоугольные по острому углу. Пусть
Обозначим
Тогда
Так как произведение секущей на ее внешнюю часть — величина постоянная для окружности, то
Так как квадрат касательной равен произведению секущей на ее внешнюю часть, то
Пусть Тогда
как угол между касательной и хордой,
заключающих дугу, на которую опирается вписанный угол
Тогда из
Из имеем:
Следовательно,

Получаем систему:
как вертикальные. Рассмотрим
По теореме
синусов имеем:
Следовательно,
б)



