а) Пусть — вторая точка пересечения окружностей, описанных около треугольников и

Четырехугольник вписан в окружность, поэтому

Аналогично четырехугольник вписан в окружность, следовательно,

Следовательно,

Следовательно, четырехугольник также вписан в окружность, то есть точка лежит на окружности, описанной около треугольника Чтд.

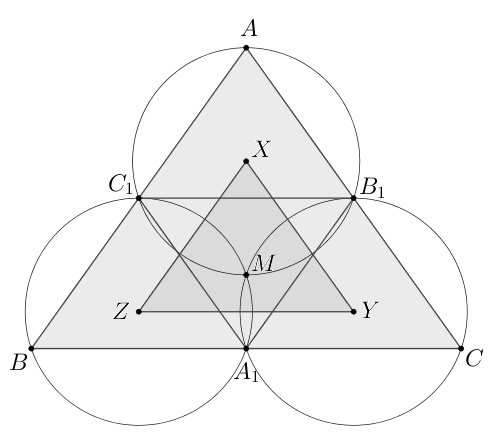
б) Докажем, что и — диаметры трех окружностей. Пусть — центр окружности, описанной около Докажем, что

Так как — точка пересечения серединных перпендикуляров к сторонам то Отсюда — вписанный, следовательно, лежит на окружности, описанной около Аналогично доказывается, что лежит на двух других окружностях, следовательно, — точка пересечения всех трех окружностей, то есть это и есть точка Из того, что следует, что и — диаметры трех окружностей.

Следовательно, если и — центры этих окружностей, то эти точки — середины отрезков и соответственно, значит, и — средние линии в и соответственно. Следовательно, стороны равны половинам сторон значит, эти треугольники подобны с коэффициентом подобия Тогда радиус окружности, впписанной в в два раза меньше радиуса окружности, вписанной в По формуле радиус окружности, вписанной в равен