Упрощённые 13 в координатах —Каталог задач по ЕГЭ - Математика

Тема Стереометрия в координатах

07 Упрощённые 13 в координатах

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела стереометрия в координатах

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#24701

В основании четырёхугольной пирамиды $SABCD$ лежит прямоугольник $ABCD$ со сторонами $AB = 12$ и $√- BC = 5 3$ . Длины боковых рёбер пирамиды $SA = 5$ , $SB = 13$ , $SD = 10$ .

а) Докажите, что $SA$ — высота пирамиды.

б) Найдите расстояние от вершины $A$ до плоскости $SBC$ .

Показать ответ и решение

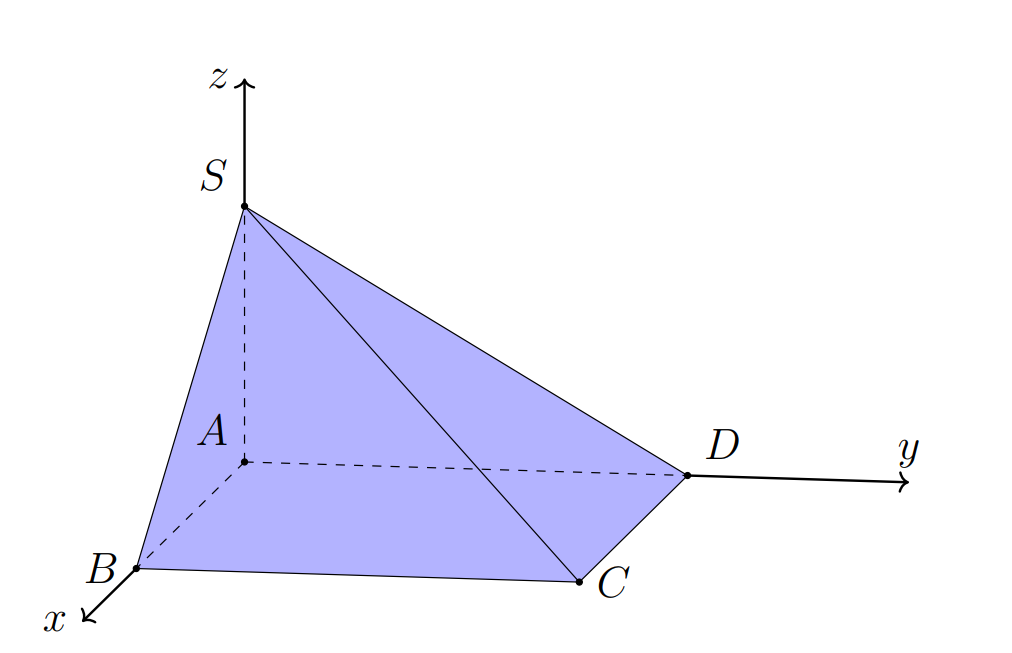
Введём прямоугольную систему координат(см. рисунок).

Точка $A$ - начало координат,

Ось $OX$ направим вдоль вектора $−A−→B$ ,

Ось $OY$ направим вдоль вектора $−−→ AD$ ,

Ось $OZ$ направим в верхнюю полупространство перпендикулярно векторам $−−→ AB$ и $−−→ AD$ .

a) Заметим, что $AB2 + SA2 = SB2$ и $SA2 + AD2 = SD2$ , поэтому $SA ⊥ AB$ , $SA ⊥ AD$ , значит, $SA ⊥ ABC$ . ч.т.д

б) Из пункта а) следует, что точка $S$ по координате $z$ имеет значение = $SA = 5$ . Тогда:

$( ) 0 A = || 0|| ( ) 0$ $( ) 12 B = || 0 || ( ) 0$ $( ) 12 C = ||5√3-|| ( ) 0$ $( ) 0 S = || 0|| ( ) 5$

$( ) ( ) ( ) ( ) x 12 0 12 −S→B : ||y|| = B − S = || 0 || − ||0|| = || 0 || ( ) ( ) ( ) ( ) z 0 5 − 5$

$( ) ( ) ( ) ( ) x 12 0 12 −S→C :|| y|| = C − S = || 5√3|| − || 0|| = || 5√3|| ( ) ( ) ( ) ( ) z 0 5 − 5$

Параметрически зададим уравнение плоскости $SBC$ :

$( ) x SBC :|| y|| = S + α⋅−S→B + β ⋅−S→C, α,β ∈ ℝ ( ) z$

$( ) ( ) ( ) ( ) x 0 12 12 SBC :|| y|| = || 0|| + α⋅|| 0|| + β ⋅|| 5√3-|| ( ) ( ) ( ) ( ) z 5 − 5 − 5$

Пусть $H$ - проекция точки $A$ на плоскость $SBC$ , тогда:

$( ) ( ) x 12α+ 12β H :|| y|| = || 5√3β || ( ) ( ) z 5− 5α − 5β$

$( ) ( ) x 12α + 12β −A−→H :|| y|| = H − A = || 5√3-β || ( ) ( ) z 5− 5α− 5β$

Очевидно, что $AH ⊥ SB$ и $AH ⊥ SC$ , следовательно, $(AH, SB) = 0$ и $(AH, SC ) = 0$

( ( ) ( ) |||| | 12α + 12β | | 12 | |||| || 5√3-β || × || 0 || = 0 ( |||| ( ) ( ) { (AH, SB) = 0 { ( 5− 5α − 5β ) (− 5 ) ( (AH, SC) = 0 = || 12α + 12β 12 = |||| || √ - || || √ -|| |||| |( 5 3β |) × |(5 3|) = 0 ||( 5− 5α − 5β − 5

( √ - {12(12α+ 12β) +5 3β ⋅0− 5(5 − 5α− 5β) = 0 = ( = 12(12α+ 12β) +75β − 5(5− 5α− 5β) = 0

( ( {169α + 169β = 25 { α = 25- = = 169 (169α + 169β + 75β = 25 ( β = 0

$( ) ( -25- ) ( ) −−→ | x| | 12⋅169 | | 5 | AH :|( y|) = |( 0 |) = 16069|( 0 |) z 5 − 5⋅12569 12$

Найдем $|AH |$

$√------------ |AH | = 61069 52 + 02 +122 = 61069 ⋅13 = 6013$

Ответ:

$ρ(A,SBC ) = 6103$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#24700

Основанием прямой треугольной призмы $ABCA1B1C1$ является прямоугольный треугольник $ABC$ с прямым углом $C$ . Прямые $CA1$ и $AB1$ перпендикулярны.

а) Доказать, что $AA = AC 1$ .

б) Найти $A1C$ , если $CC1 = 5$ .

Показать ответ и решение

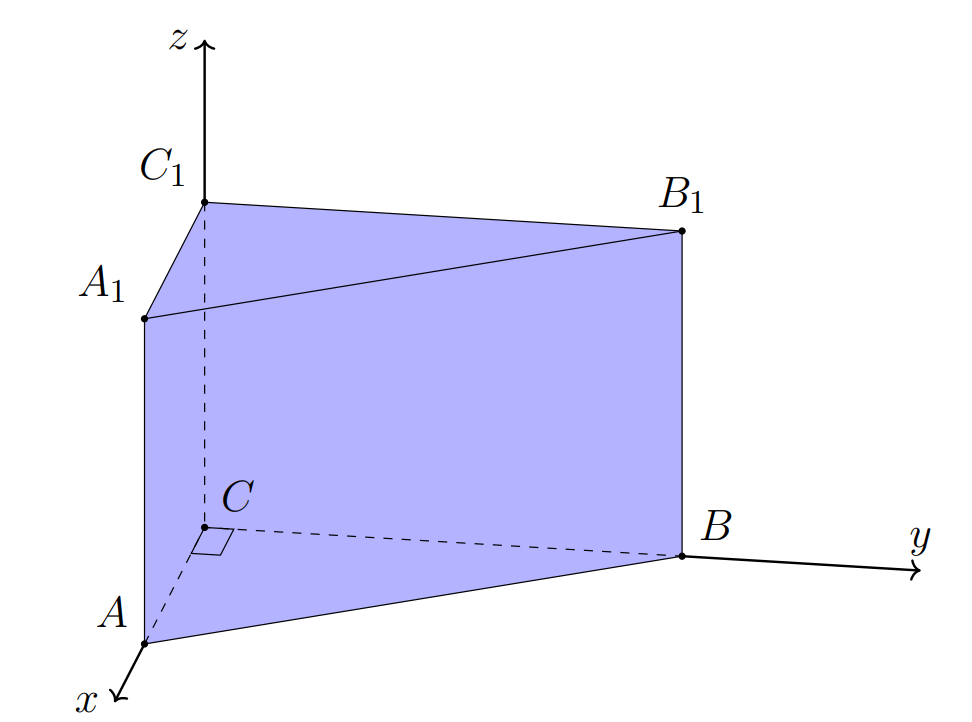
Введём прямоугольную систему координат(см. рисунок).

Точка $C$ - начало координат,

Ось $OX$ направим вдоль вектора $−C→A$ ,

Ось $OY$ направим вдоль вектора $−−→ CB$ ,

Ось $OZ$ направим вдоль вектора $−−→ CC1$ .

Пусть $AC = a,BC = b,AB = c,AA1 = h$

$( ) 0 || || C = ( 0) 0$ $( ) a || || A = ( 0) 0$ $( ) 0 || || B = (b) 0$ $( ) 0 || || C1 = (0) h$ $( ) a || || A1 = (0) h$ $( ) 0 || || B1 = ( b) h$

$( x) ( a) ( 0) (a) −−→ || || || || || || || || CA1 :( y) = A1 − C = ( 0) − ( 0) = (0) z h 0 h$

$( ) ( ) ( ) ( ) −−→ | x| | 0| |a| |− a| AB1 :|( y|) = B1 − A = |( b|) − |(0|) = |( b |) z h 0 h$

а) Из условия, что $CA1 ⊥ AB1$ следует, что $−−→ −−→ −−→ −−→ CA1 ⊥ AB1 → (CA1, AB1) = 0$

$( ) ( ) a − a (−C−A→1,−A−B→1 ) = || 0|| × || b|| = a⋅(− a)+ 0 ⋅b+ h⋅h = 0 ( ) ( ) h h$

− a2 + h2 = 0

a = h

Так как $AC = a,AA = h 1$ , $AC = AA 1$ ч.т.д.

б) Из условия $CC1 = 5 → AA1 = 5$

Из доказанного ранее $AC = AA1 = 5$

По теореме Пифагора для треугольника $AA1C$ :

$A C2 = AA2 + AC2 = 52 + 52 1 1$

$√ - A1C = 5 2$

Ответ:

$√- A1C = 5 2$

Ошибка.
Попробуйте повторить позже

Задача 3#24699

Точки $N$ и $M$ - середины рёбер $AD$ и $CC1$ куба $ABCDA1B1C1D1$ соответственно.

а) Доказать, что прямая $BM ⊥ B1N$

б) Пусть $H$ - проекция точки $M$ на прямую $B N 1$ . Найти $B H 1$ , если $AB = 12$

Показать ответ и решение

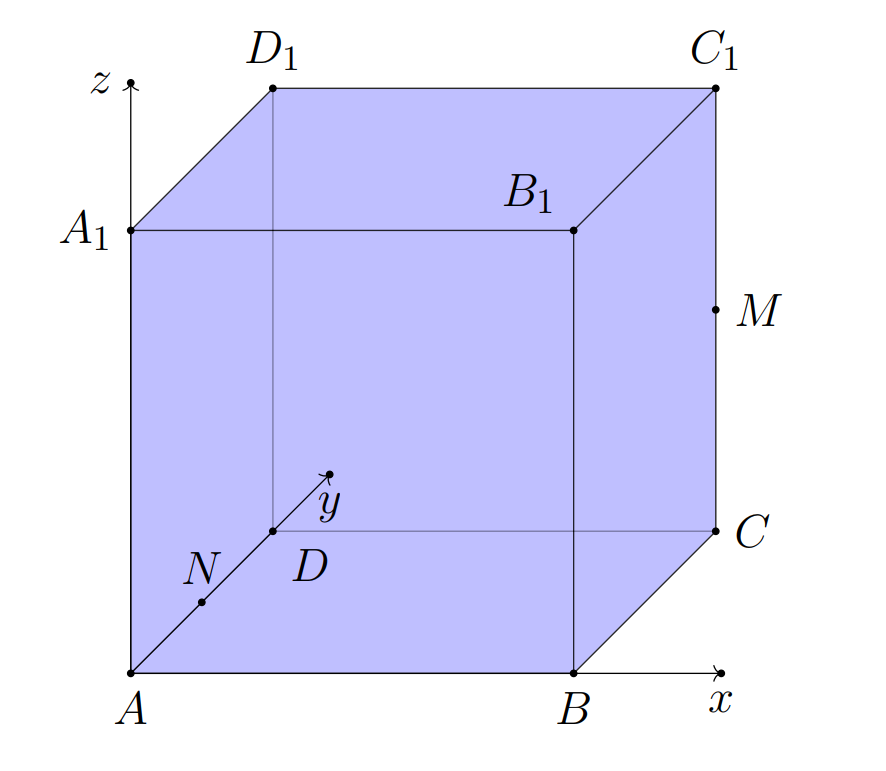
Введём прямоугольную систему координат(см. рисунок).

Точка $A$ - начало координат,

Ось $OX$ направим вдоль вектора $−A−→B$ ,

Ось $OY$ направим вдоль вектора $−−→ AD$ ,

Ось $OZ$ направим вдоль вектора $−−→ AA1$ .

Пусть $AB = a$ , тогда имеем следующие координаты точек:

$( ) 0 || || A = ( 0) 0$ $( ) a || || B = (0) 0$ $( ) a || || C = ( a) 0$ $( ) 0 || || D = ( a) 0$

$( 0) || || A1 = ( 0) a$ $( a) || || B1 = ( 0) a$ $(a) || || C1 = (a) a$ $( 0) || || D1 = ( a) a$

Так как $N$ - середина $AD$ :

$( ) ( ) ( ) ( ) ( ) ( ) x 0 0− 0 0 0 0 || || 1−−→ || || 1 || || || || || a|| || a|| N :( y) = A + 2AD = ( 0) + 2 ⋅( a− 0) = ( 0) + ( 2) = ( 2) z 0 0− 0 0 0 0$

Так как $M$ - середина $CC1$ :

$( ) ( ) ( ) ( ) ( ) ( ) x a a− a a 0 a M :|| || = C + 1−C−C→ = || || + 1⋅|| || = || || + || || = || || (y ) 2 1 ( a) 2 ( a− a) ( a) ( 0) ( a) z 0 a− 0 0 a2 a2$

а) Прямые перпендикулярны, если перпендикулярны их направляющие вектора. То есть, $BM ⊥ B1N$ , если $−B−M→ ⊥ −B−−→N 1$ . Найдем вектора $−−B→M ,−B−−→N 1$ :