Ошибка.
Попробуйте повторить позже
Середина стороны
выпуклого четырёхугольника
равноудалена от
всех его вершин. Найдите
если
а углы
и
четырёхугольника
равны соответственно
и
Так как точка равноудалена от всех вершин
то
Значит, около четырехугольника можно описать окружность с центром
в точке
и радиусом
Пусть
Так как четырехугольник вписанный, то сумма его противоположных углов
равна
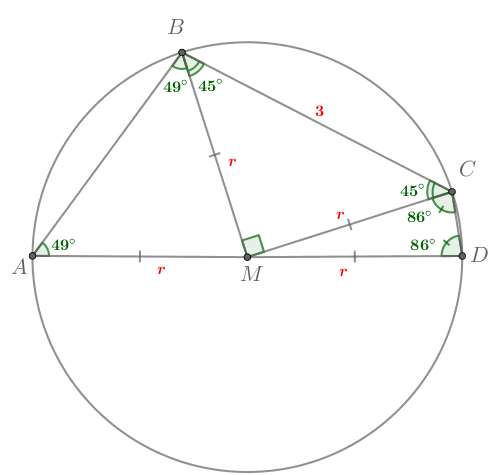
Найдем четырехугольника
Так как в треугольнике
то он равнобедренный. В
равнобедренном треугольнике углы при основании равны, поэтому
Найдем
Так как в треугольнике
то треугольник
—
равнобедренный. В равнобедренном треугольнике углы при основании равны,
поэтому
В по теореме о сумме углов треугольника:
Тогда треугольник — прямоугольный. По теореме Пифагора:
Найдем
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Четырехугольник со сторонами
и
вписан в
окружность. Диагонали
и
пересекаются в точке
причем
Найдите радиус окружности, описанной около этого
четырехугольника.
Проведем Тогда
как соответсвенные углы,
образованные параллельными прямыми
и
и секущей
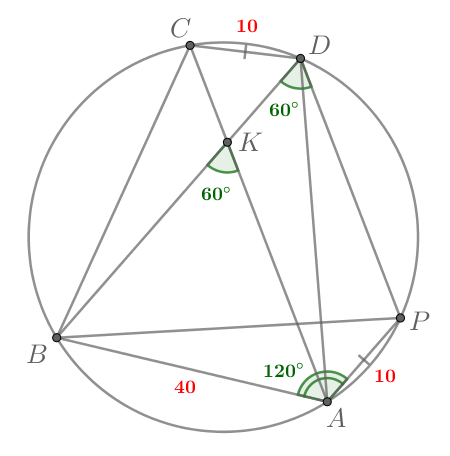
Рассмотрим четырехугольник Параллельные прямые
и
высекают на окружности равные дуги, следовательно, хорды, которые их
стягивают, равны, то есть
Так как — вписанный четырехугольник, то сумма его противоположных
углов равна
значит,
Рассмотрим треугольник Запишем теорему косинусов для него:
Пусть радиус окружности равен По теореме синусов для треугольника
Значит, радиус окружности равен
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Середина стороны
выпуклого четырёхугольника
равноудалена
от всех его вершин. Найдите
если
а углы
и
четырехугольника
равны соответственно
и
Так как точка равноудалена от всех вершин
то
Значит, около четырехугольника можно описать окружность с центром
в точке
и радиуса
Пусть
Так как четырехугольник вписанный, то сумма противоположных углов равна
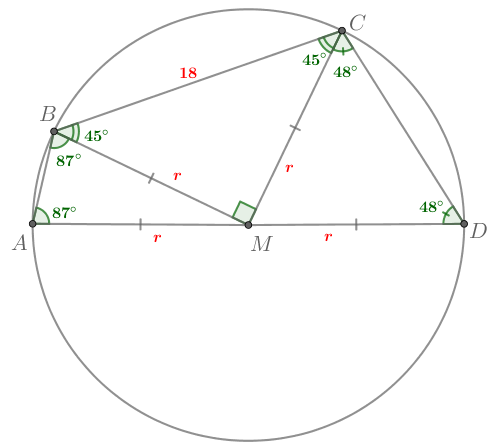
Найдем четырехугольника
Так как в то
— равнобедренный. В
равнобедренном треугольнике углы при основании равны, поэтому
Найдем
Так как в то
— равнобедренный. В
равнобедренном треугольнике углы при основании равны, поэтому
В по теореме о сумме углов треугольника:
Тогда — прямоугольный. По теореме Пифагора:
Найдем
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Четырёхугольник со сторонами
и
вписан в
окружность. Диагонали
и
пересекаются в точке
причём
. Найдите радиус окружности, описанной около этого
четырёхугольника.
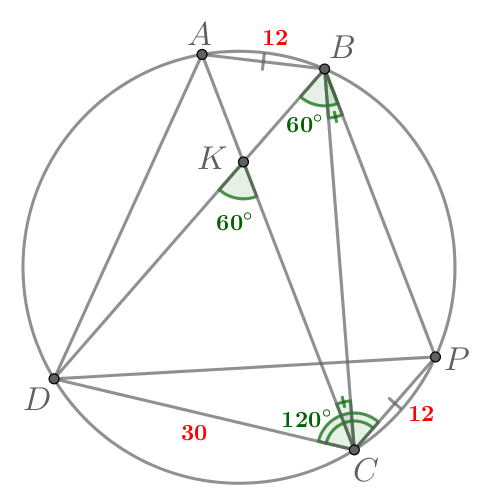
Так как и
— вертикальные, то
Проведем прямую через точку параллельную
Пусть она пересекает
окружность в точке
Так как то
как накрест лежащие при
параллельных прямых.
Вписанный угол равен половине дуги, на которую он опирается, поэтому
Так как то дуги
и
на которые опираются эти
углы, равны.
Хорды окружности, стягивающие равные дуги, равны, поэтому
Четырехугольник вписанный. По свойству вписанного четырехугольника
Рассмотрим треугольник По теореме косинусов
Тогда
Пусть — радиус окружности. В треугольнике
по теореме
синусов
Найдем
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, получен верный ответ | 2 |
| Ход решения верный, все его шаги присутствуют, но допущена арифметическая ошибка | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |



