Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны. Докажите,
что углы
и
также равны.
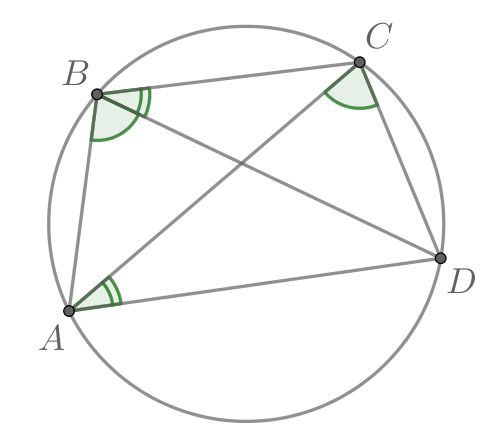
и опираются на один отрезок
Тогда по признаку
вписанного четырёхугольника
— вписанный.
По свойству вписанного четырёхугольника углы, опирающиеся на одну сторону,
равны, следовательно,
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны. Докажите,
что углы
и
также равны.
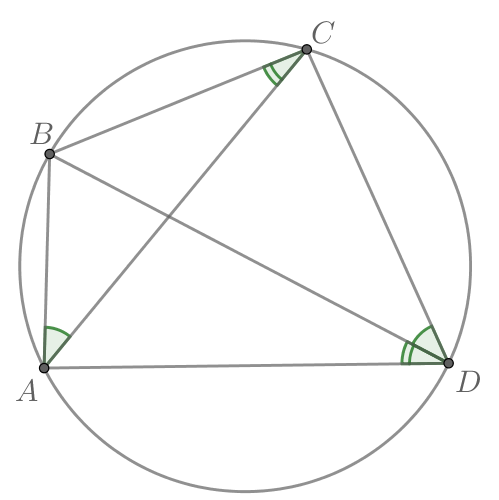
Так как и они опираются на один отрезок
то по критерию
вписанности четырехугольника
— вписанный.
Тогда как вписанные углы, опирающиеся на дугу
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны. Докажите, что углы
и
также
равны.
В четырехугольнике углы, опирающиеся на сторону
равны, значит, четырехугольник
— вписанный.
Тогда углы, опирующиеся на сторону
также равны, то есть
Что и требовалось доказать.
![]()
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Известно, что около четырёхугольника можно описать окружность и что
продолжения сторон
и
четырёхугольника пересекаются в точке
Докажите, что треугольники
и
подобны.
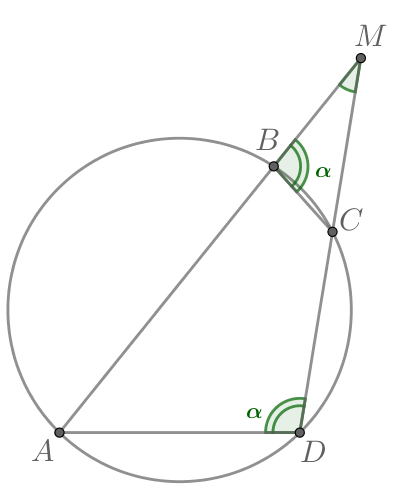
Пусть Тогда
так как сумма
противоположных углов вписанного четырёхугольника равна
Сумма смежных углов равна поэтому
Рассмотрим треугольники и
— общий,
Таким образом, треугольники и
подобны по двум углам.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Окружности с центрами в точках и
пересекаются в точках
и
причём точки
и
лежат по одну сторону от
прямой
Докажите, что
Способ 1.
Проведём отрезки
и
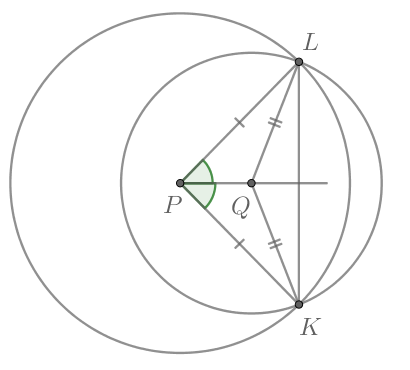
Тогда как радиусы окружности с центром в точке
как радиусы окружности с центром в точке
Рассмотрим треугольники
и
В них
— общая сторона,
Тогда треугольники
и
равны по трём сторонам. Следовательно,
как
соответственные элементы равных треугольников.
Рассмотрим равнобедренный треугольник В нём
— биссектриса,
проведённая к основанию, следовательно, и высота. Значит,
Способ 2.
Пусть — середина хорды
Проведём отрезки
и
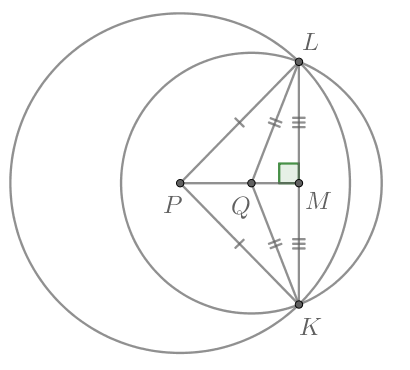
В треугольнике
как радиусы окружности с центром в точке
поэтому треугольник
равнобедренный. Тогда по свойству равнобедренного
треугольника медиана
проведённая к основанию, является высотой, то есть
В треугольнике
как радиусы окружности с центром в точке
поэтому треугольник
равнобедренный. Значит,
— медиана и
высота, и
Две прямые, перпендикулярные третьей прямой, параллельны. Прямые и
перпендикулярны прямой
и проходят через точку
значит, точки
лежат на одной прямой, перпендикулярной
Значит,
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Окружности с центрами в точках и
не имеют общих точек, и окружности не
лежат одна внутри другой. Внутренняя общая касательная к этим окружностям
делит отрезок, соединяющий их центры, в отношении
Докажите, что
диаметры этих окружностей относятся как
Пусть внутренная общая касательная касается окружности с центром в точке в
точке
окружности с центром в точке
в точке
Обозначим за
точку
пересечения
и
По условию
Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то
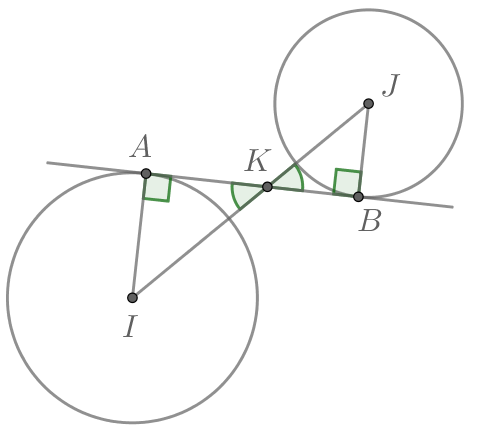
Рассмотрим треугольники и
как вертикальные. Тогда
по двум углам.
Запишем коэффициент подобия:
Пусть — диаметр окружности с центром в точке
— диаметр
окружности с центром в точке
Тогда
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Окружности с центрами в точках и
не имеют общих точек, и ни одна из
них не лежит внутри другой. Внутренняя общая касательная к этим окружностям
делит отрезок, соединяющий их центры, в отношении
. Докажите, что
диаметры этих окружностей относятся как
Пусть — центр первой окружности,
— центр второй,
и
— точки
касания общей касательной с первой и второй окружностями соответственно.
Пусть
— точка пересечения
и
Тогда по условию
Проведем радиусы и
Так как
— общая касательная к
окружностиям, то
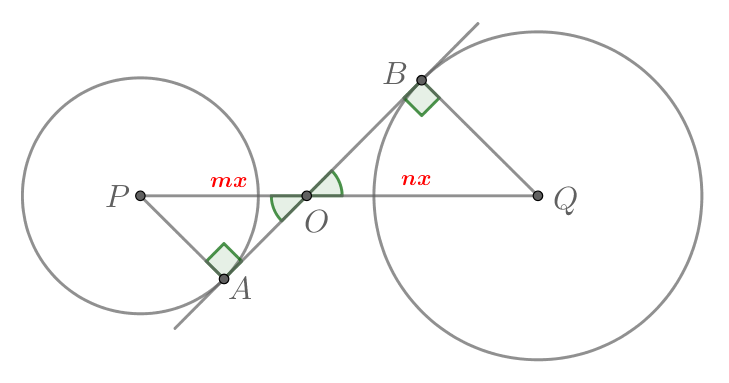
Заметим, что как вертикальные. Тогда треугольники
и
подобны по двум углам, следовательно,
Диаметр любой окружности равен ее удвоенному радиусу, то есть
Тогда
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Окружности с центрами в точках и
не имеют общих точек, и окружности не лежат одна внутри другой. Внутренняя
общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении
Докажите, что радиусы
этих окружностей относятся как
Обозначим точки касания за и
а точку пересечения касательной и прямой
за
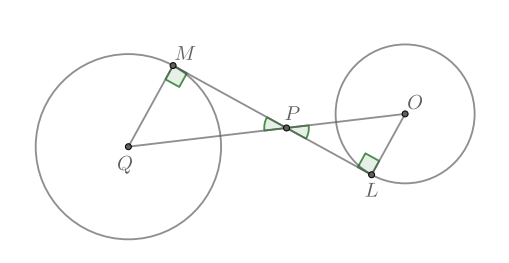
Рассмотрим треугольники и
Они подобны по двум углам:
как вертикальные,
как углы между касательной и радиусом. Тогда
Из условия известно, что тогда
При этом и
— радиусы окружностей, то есть радиусы этих окружностей относятся как
что и требовалось
доказать.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |



