Ошибка.
Попробуйте повторить позже
Основания и
трапеции
равны соответственно 5 и 45,
Докажите, что треугольники
и
подобны.
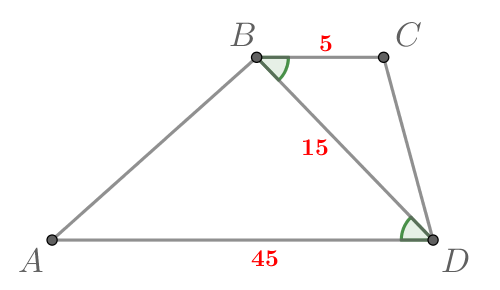
Рассмотрим треугольники и
- 1.
- Так как
то
как внутренние накрест лежащие.
- 2.
Тогда по двум сторонам и углу между ними.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Через точку пересечения диагоналей параллелограмма
проведена
прямая, пересекающая стороны
и
в точках
и
соответственно.
Докажите, что отрезки
и
равны.
Рассмотрим треугольники и
- 1.
так как диагонали параллелограмма точкой пересечения делятся пополам;
- 2.
как вертикальные;
- 3.
как внутренние накрест лежащие углы при параллельных прямых
и
и секущей
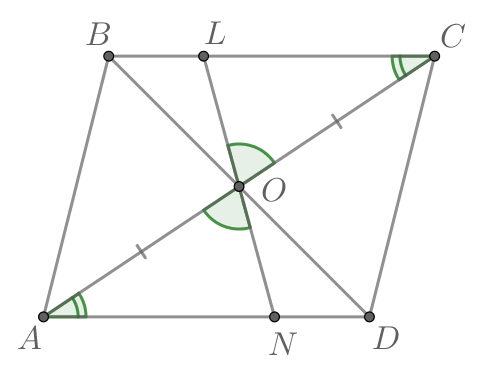
Тогда треугольники и
равны по стороне и двум прилежащим к
ней углам. Значит,
как соответственнные элементы равных
треугольников.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Через точку пересечения диагоналей параллелограмма
проведена
прямая, пересекающая стороны
и
в точках
и
соответственно.
Докажите, что отрезки
и
равны.
Проведем
Тогда
— параллелограмм, так как
его противоположные стороны параллельны. Следовательно,
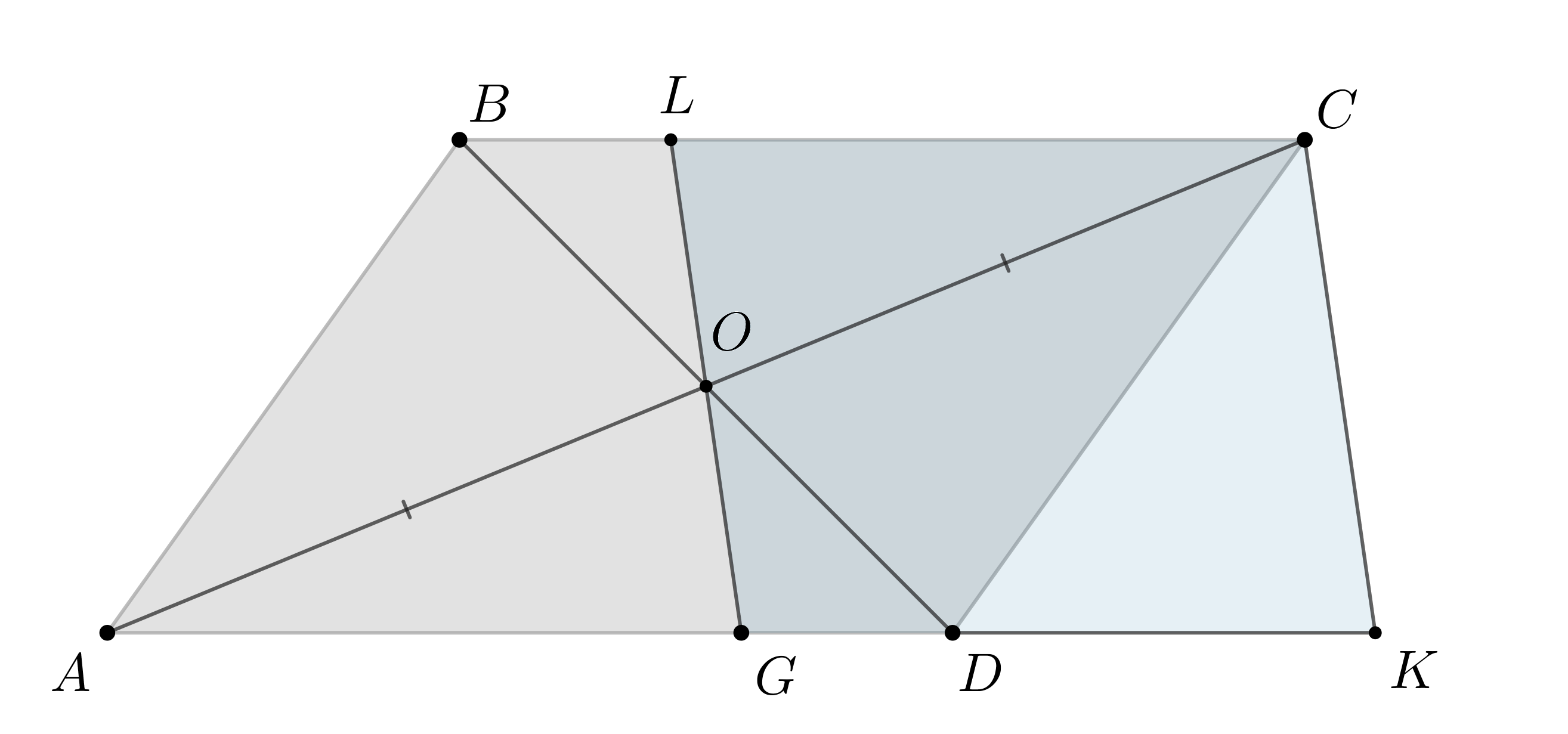
Так как и
— середина
то по теореме Фалеса
— середина
следовательно,
Таким образом,
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В параллелограмме проведены высоты
и
к сторонам
и
соответственно, при этом
Докажите, что
—
ромб.
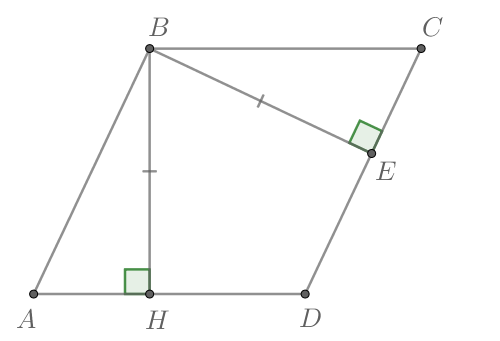
Площадь параллелограмма равна произведению основания на высоту, проведённой к этому основанию, поэтому
Значит,
Так как то
По свойству параллелограмма
Так как
то
Значит,
— ромб по определению.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В трапеции с основаниями
и
диагонали пересекаются в точке
Докажите, что площади треугольников
и
равны.
Опустим высоты и
трапеции
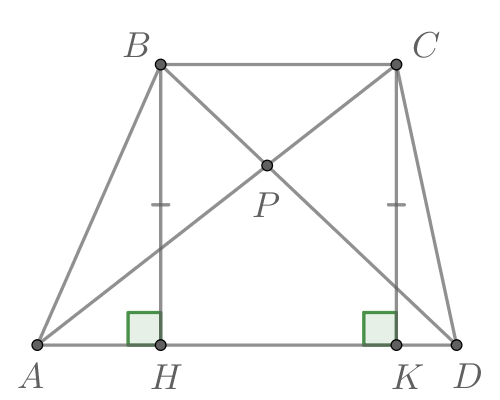
Рассмотрим треугольники и
В них проведены высоты
и
соответственно. Так как площадь треугольника равна половине произведения
основания на высоту, то
как расстояние между двумя параллельными прямыми. Значит,
Так как и
то
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Сторона параллелограмма
вдвое больше стороны
Точка
— середина стороны
Докажите, что
— биссектриса угла
Так как — середина
то
По условию
значит,
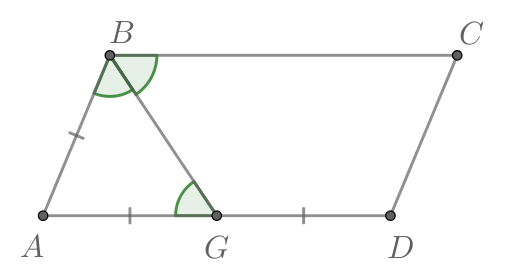
Рассмотрим треугольник
следовательно, треугольник
равнобедренный. В равнобедренном треугольнике углы при основании
равны, поэтому
Так как накрест лежащие углы при параллельных прямых равны, и
то
Таким образом,
Значит, — биссектриса
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Сторона параллелограмма
вдвое больше стороны
Точка
— середина стороны
Докажите, что
— биссектриса угла
Так как — середина
то
По условию
значит,
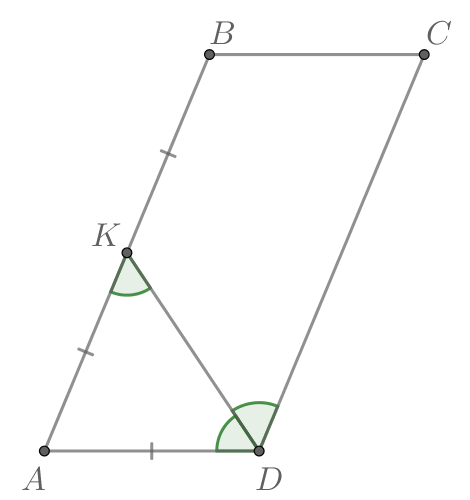
Рассмотрим треугольник
следовательно, треугольник
равнобедренный. В равнобедренном треугольнике углы при основании
равны, поэтому
Так как накрест лежащие углы при параллельных прямых равны, и
то
Таким образом,
Значит, — биссектриса
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
параллелограмма
пересекаются в точке
лежащей на стороне
Докажите, что
— середина
Углы и
равны, так как
— биссектриса. Также углы
и
равны, так как
— биссектриса.
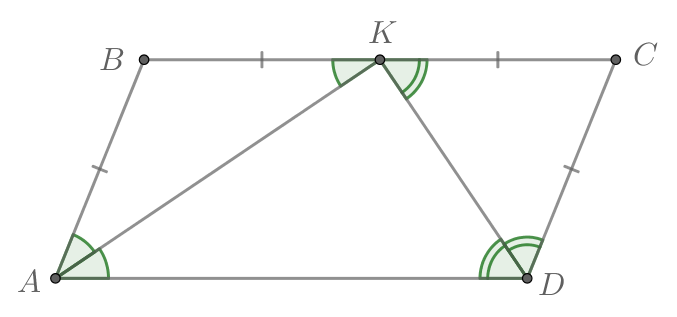
Противоположные стороны в параллелограмме параллельны, поэтому
и
как накрест лежащие. Получаем два
равнобедренных треугольника
и
В параллелограмме противоположные стороны равны, то есть в
силу равнобедренности треугольников
Тогда точка
— середина
стороны
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
трапеции
пересекаются в точке
лежащей
на стороне
Докажите, что точка
равноудалена от прямых
и
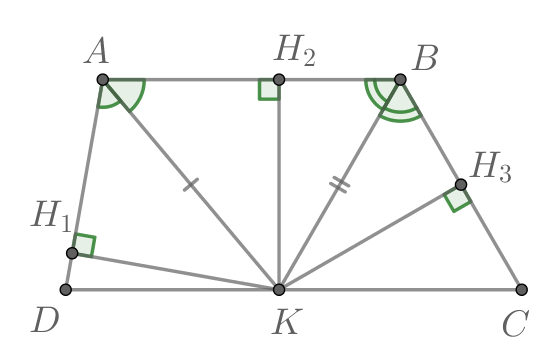
Проведем перпендикуляры из точки
к прямым
соответственно.
Требуется доказать, что точка равноудалена от прямых
и
то есть, что длины перпендикуляров из точки
к этим прямым равны, то
есть:
Рассмотрим и
- 1.
- 2.
- 3.
– общая сторона.
=
по стороне и двум прилежащим к ней углам. Тогда
как соответственные элементы равных треугольников.
Рассмотрим и
- 1.
- 2.
- 3.
– общая сторона.
=
по стороне и двум прилежащим к ней углам. Тогда
как соответственные элементы равных треугольников.
Получаем:
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
В параллелограмме диагонали
и
пересекаются в точке
Докажите, что площадь параллелограмма
в четыре раза больше площади
треугольника
Проведём через точку высоту
параллелограмма
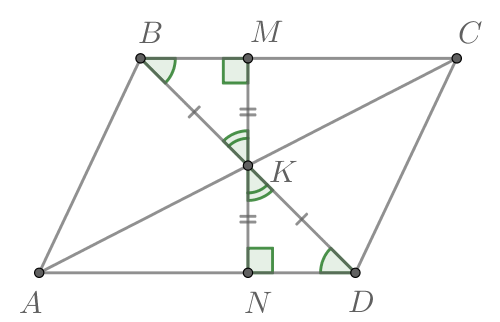
Рассмотрим треугольники и
- 1.
как накрест лежащие при параллельных прямых;
- 2.
как вертикальные;
- 3.
так как диагонали параллелограмма точкой пересечения делятся пополам.
Тогда треугольники и
равны по стороне и двум прилежащим к
ней углам.
как соответственные элементы равных
треугольников.
Площадь треугольника равна половине произведения основания на высоту:
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Внутри параллелограмма выбрали произвольную точку
Докажите,
что сумма площадей треугольников
и
равна половине площади
параллелограмма.
Проведем высоту в
в
высоту
По формуле площади
треугольника
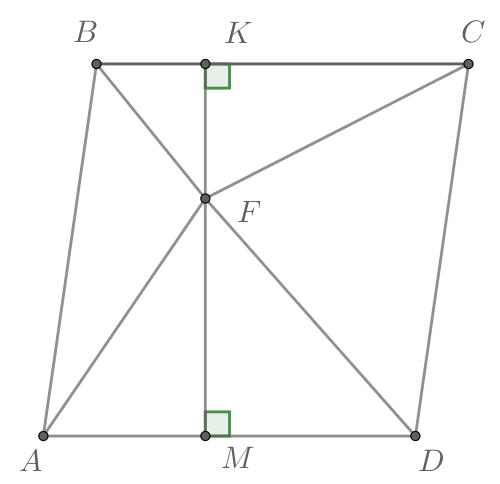
Тогда
По свойству параллелограмма противоположные стороны равны, то есть
поэтому
По определению параллелограмма по построению
и
поэтому по свойству параллельных прямых
Так как
и
имеют общую точку
и перпендикулярны прямой
то
и
лежат на одной прямой, поэтому:
Таким
образом,
При этом – высота параллелограмма
так как
поэтому по формуле площади параллелограмма
Получаем
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
На средней линии трапеции с основаниями
и
выбрали
произвольную точку
Докажите, что сумма площадей треугольников
и
равна половине площади трапеции.
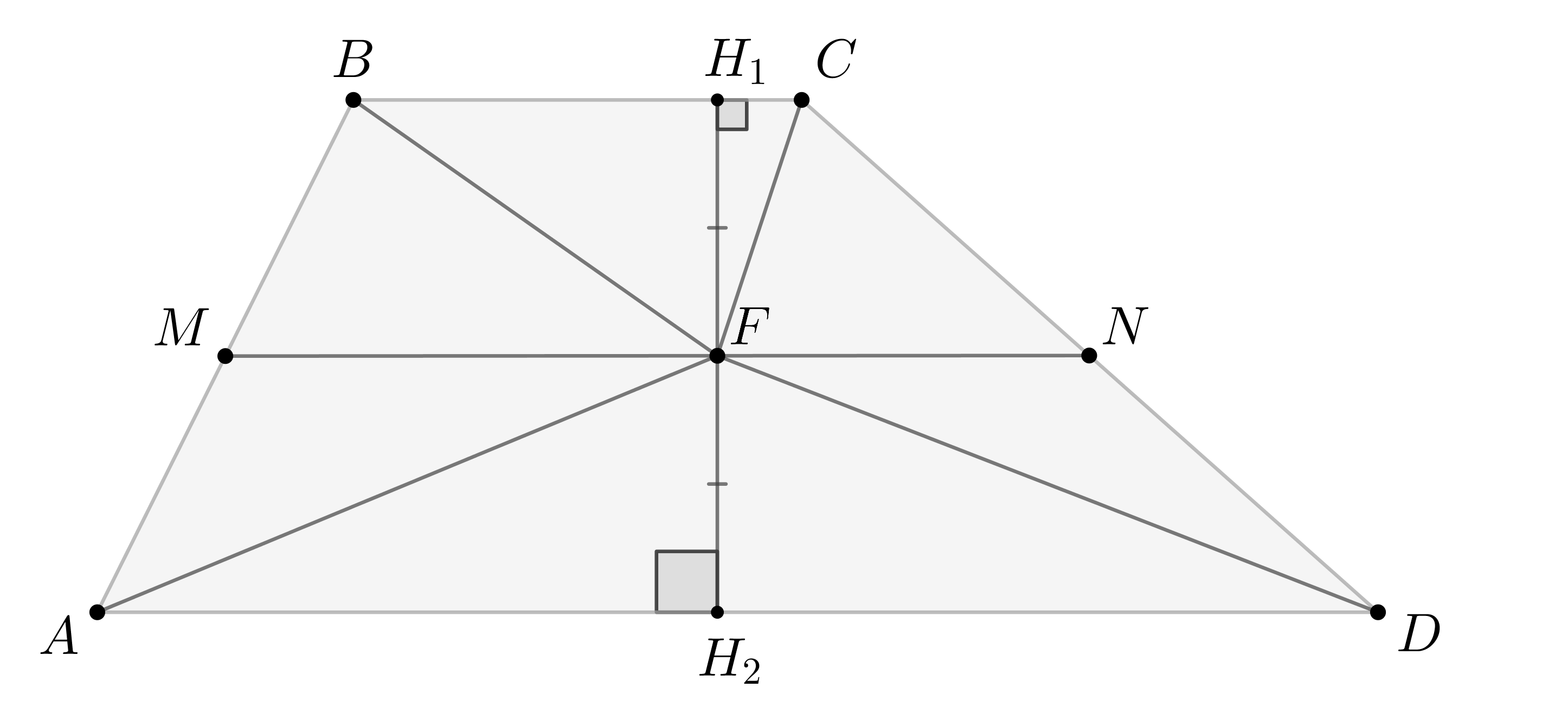
Пусть — средняя линия. Так как
то расстояние от точки
до
оснований трапеции одинаково, то есть
Действительно,
следовательно, точки
и
лежат на одной прямой. Тогда по теореме Фалеса для
и
и
так как
то
где
— высота трапеции.
Тогда
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Точка — середина боковой стороны
трапеции
Докажите, что
площадь треугольника
равна сумме площадей треугольников
и
Опустим перпендикуляры и
из точки
на прямые
и
соответственно. Тогда
следовательно
Так как две прямые, перпендикулярные третьей, параллельны, то
точки
лежат на одной прямой, то есть
— высота трапеции
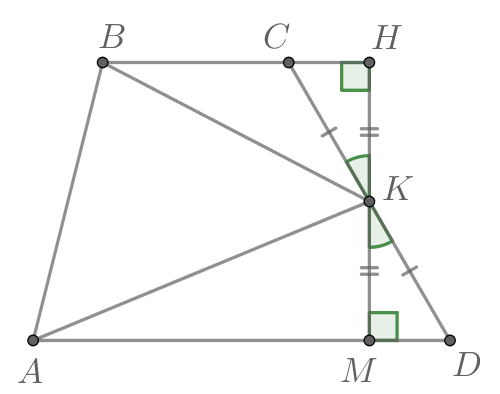
Рассмотрим треугольники и
В них
по условию,
как вертикальные. Тогда треугольники
и
равны по гипотенузе и острому углу. Следовательно,
как соответственные элементы равных треугольников.
Так как площадь треугольника равна половине произведения высоты на основание, то
Значит,
Так как то
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Дана равнобедренная трапеция Точка
лежит на основании
и
равноудалена от концов другого основания. Докажите, что
— середина
основания
Так как точка равноудалена от концов основания
то
Тогда
треугольник
— равнобедренный. В равнобедренном треугольнике углы при
основании равны, поэтому
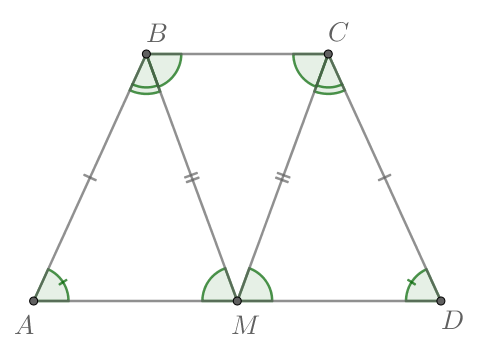
Так как накрест лежащие углы при параллельных прямых равны, то
В равнобедренной трапеции углы при основании равны, поэтому
По теореме о сумме углов треугольника
Рассмотрим треугольники и
так как трапеция
равнобедренная,
Тогда треугольники
и
равны по двум сторонам и углу между ними.
как
соответственные элементы равных треугольников. Значит, точка
— середина
основания
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Ошибка.
Попробуйте повторить позже
Точка — середина боковой стороны
трапеции
, а
Докажите, что трапеция
прямоугольная.
Отметим точку — середину
Так как точка — середина
то
— средняя линия трапеции
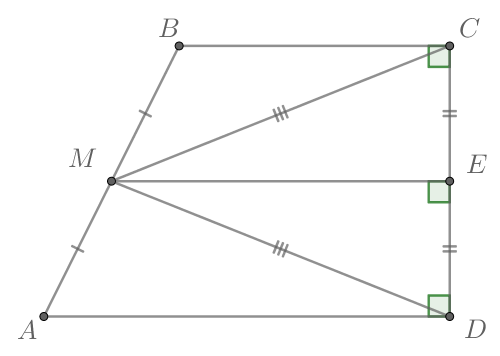
По свойству средней линии трапеции
Рассмотрим Так как
то
— равнобедренный.
— медиана равнобедренного треугольника, проведенная к основанию. По
свойству медианы в равнобедренном треугольнике, проведенной к основанию,
— высота.
Тогда
Так как перпендикулярная к одной из двух параллельных прямых, перпендикулярна и к другой прямой, то
Тогда
то есть трапеция — прямоугольная.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | 2 |
| Доказательство в целом верное, но содержит неточности | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |



