Произвольные последовательности чисел —Каталог задач по ЕГЭ - Математика

Ошибка.
Попробуйте повторить позже

Задача 1#2021

Верно ли, что при любом $k > 0$ последовательность $√ ------ an = n + k$ не убывает?

Показать ответ и решение

Зафиксируем произвольное $k > 0$ .

Рассмотрим функцию $√ ------ f(x) = x + k$ при $x > 0$ .

При $x > 0$ :

′ 1 f (x) = --√------ > 0. 2 x + k

Таким образом, функция $f$ возрастает на $(0;+ ∞ )$ , тогда $f (n + 1) > f(n)$ – при всяком $n ∈ ℕ$ , то есть последовательность $an$ возрастает, а следовательно, она не убывает.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 2#730

Верно ли, что при любом $k > 0$ последовательность $√ ------ √ -- an = n + k − n$ убывает?

Показать ответ и решение

Зафиксируем произвольное $k > 0$ .

Рассмотрим функцию $√ ------ √ -- f(x) = x + k − x$ при $x > 0$ .

При $x > 0$ :

1 1 √x-− √x-+--k- f ′(x) = --√------− -√---= --√------√---. 2 x + k 2 x 2 x + k x

Так как $0 < x < x + k$ , то $√ -- √ ------ x < x + k$ , следовательно, $f ′(x) < 0$ при $x > 0$ , то есть функция $f$ убывает на $(0;+ ∞ )$ , тогда $f (n + 1) < f(n)$ – при всяком $n ∈ ℕ$ , то есть последовательность $an$ убывает.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 3#72215

На доске написано 30 различных натуральных чисел, каждое из которых либо оканчивается цифрой 1, либо четное. Сумма всех чисел равна 771.

а) Может ли на доске быть выписано ровно четыре числа, оканчивающихся цифрой 1?

б) Может ли на доске быть выписано ровно 13 чисел, оканчивающихся цифрой 1?

в) Найдите наименьшее возможное количество чисел, оканчивающихся единицей, среди выписанных на доске.

Показать ответ и решение

а) Если на доске записано 4 числа, оканчивающихся на 1, то их сумма чётна, так как сумма чётного количества нечётных чисел чётна.

Если на доске записано 26 чётных чисел, то их сумма чётна, так как сумма любого количества чётных чисел чётна.

Таким образом, сумма всех 30 чисел также будет чётной. Но число 771 нечётно, значит, ответ на пункт отрицательный.

б) Рассмотрим сумму 30 наименьших натуральных чисел таких, что 13 из них оканчиваются на 1, а остальные 17 — чётные.

По формуле суммы арифметической прогрессии 17 последовательных чётных чисел $S1$ имеем:

2+ 34 S1 = --2--⋅17= 306.

Запишем сумму 13 наименьших оканчивающихся на 1 чисел $S2$ :

S2 = 1 +11+ 21+ 31+ 41+ 51+ 61+ 71+ 81+ 91+ 101 +111+ 121= 793.

То есть $S1+ S2 > 771,$ при этом мы рассматривали наименьший возможный пример чисел, значит, для всех остальных наборов сумма будет еще больше, поэтому ответ на этот пункт также отрицательный.

в) Пусть на доске записано $n$ чисел, оканчивающихся на 1. Тогда на этой же доске записано $30− n$ чётных чисел.

Запишем сумму $S1$ первых $n$ чисел как сумму суммы $n$ единиц и $n$ наименьших натуральных последовательных чисел, кратных 10:

S1 = 1 ⋅n + 0+-10(n-−-1)-⋅n= 5n2− 4n. 2

Запишем сумму $S2$ первых $30 − n$ наименьших натуральных чётных чисел:

S2 = 2+-2-+2((30-− n-)− 1) ⋅(30− n)= (31− n)⋅(30 − n) =n2 − 61n +930. 2

Сумма $S1+ S2 ≤ 771$ по условию:

2 2 5n − 4n+ n − 61n+ 930≤ 771,

2 6n − 65n+ 159≤ 0.

Найдём нули левой части через формулу дискриминанта:

D = 652− 4 ⋅6⋅159= 4225 − 3816= 409.

$⌊ √ --- n = 65−---409, || 1 12√ --- ⌈n = 65+---409. 2 12$

По методу интервалов получаем $n∈ [65−√409; 65+√409] 12 12$ .

Определим положение левой границы отрезка.

Раз $400< 409< 441$ , то $20 < √409< 21.$ Тогда:

√--- 65-− 21 < 65−-409-< 65−-20, 12 12 12

2 65− √409 3 33 < ---12----< 34.

Так как $n ∈ℕ$ , то $n ≥4.$ Однако если $n$ чётно, то (как показано в пункте а)) мы встречаем противоречие, поэтому на самом деле $n ≥ 5.$

Пример для $n = 5:$

1+ 11+ 21+ 31+ 41+ 2+ 4+ ...+24 +26+ 484= 771.

Ответ:

а) Нет.

б) Нет.

в) 5. Пример: $1,11,21,31,41,2,4,...,24,26,484.$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в пунктах а), б) и в)	4

Обоснованно получен верный ответ в пункте в) и обоснованно получен верный ответ в пунктах а) или б)	3

Обоснованно получены верные ответы в пунктах а) и б),	2
ИЛИ
обоснованно получен верный ответ в пункте в)

Обоснованно получен верный ответ в пунктах а) или б)	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 4#60162

В строку записаны $n$ чисел, причем суммы любых трех подряд равна 7, а сумма всех равна 20.

1) Может ли $n$ равняться 12?

2) Может ли $n$ равняться 10? Найдите седьмое число.

Показать ответ и решение

1) Если $n= 12,$ то числа можно разбить на 4 группы по 3 подряд идущих, значит, сумма всех чисел равна $7⋅4 =28,$ а не 20.

2) Первое, второе и третье числа образуют тройку, и их сумма равна 7. Аналогично — числа с номерами 4, 5, 6 и 8, 9, 10. Значит, сумма всех чисел, кроме седьмого, равна $7⋅3= 21,$ следовательно, седьмое равно $20− 21= − 1.$

Пример такой строки:

−1, 4, 4, −1, 4, 4, −1, 4, 4, − 1

Ответ:

1) Нет, не может

2) Может, $− 1$

Ошибка.
Попробуйте повторить позже

Задача 5#46570

Гринч позеленел и решил похитить Рождество и спрятал все подарки в своей пещере на самой вершине горы в сундуке, а на сундук повесил замок. Код замка представляет собой последовательность чисел, первый член которой равен 0, а каждый следующий отличается от предыдущего на единицу.

а) Может ли 22-й член последовательности быть равен нулю?

б) Может ли среди первых 11 членов последовательности быть ровно шесть двоек?

в) Для каждого целого числа $i$ определим $ki$ — количество чисел, равных $i,$ среди первых восьми членов последовательности. Какое наибольшее значение может принимать произведение всех ненулевых $ki?$ Например, если среди первых восьми членов последовательности три нуля, одна двойка и четыре единицы, то $k0 = 3,$ $k1 =4,$ $k2 = 1,$ остальные равны нулю. Произведение ненулевых $ki$ в этом случае равно $3⋅4⋅1= 12.$

$PIC$

Показать ответ и решение

а) Любые два соседних члена последовательности отличаются на 1, следовательно, они разной четности. Первый член 0 — четный, четность чередуется, значит, все члены с нечетными номерами четны, а с четными номерами — нечетны. Таким образом, 22-ой член последовательности должен быть нечетным и не может быть равен нулю.

б) Среди первых 11 членов последовательности ровно 6 четных, то есть это те члены, у которых нечетные индексы:

1, 3, 5, 7, 9, 11

При этом мы знаем, что первый четный член равен нулю. Получаем противоречие, так как шесть двоек невозможно разместить на пяти свободных позициях для четных чисел.

в) Рассмотрим ненулевые $ki.$ Их сумма должна равняться 8, так как они равны количествам вхождений различных чисел в первую восьмерку.

Решим сначала другую задачу. Найдем максимально возможное значение, которое может принимать произведение нескольких натуральных чисел, сумма которых равна 8. Далее разберемся, какое наибольшее значение произведения реализуемо в условиях нашей задачи.

Пусть среди наших чисел с суммой 8 есть хотя бы одна единица, а их произведение равно $p,$ то есть имеется следующий набор чисел:

1, a1, ..., ak

Тогда, если мы возьмем набор $a1+ 1,...,ak,$ то сумма чисел в нем будет также равна 8, а произведение будет больше, чем в исходном. Таким образом, можем сделать вывод, что максимум произведения не может достигаться в наборе, в котором есть хотя бы одна единица.

Рассмотрим всевозможные наборы чисел с суммой 8, такие, что ни одно из чисел не равно единице, чтобы найти максимум произведения чисел в таком наборе.

Рассмотрим, чему может равняться количество чисел в наборе.

В наборе 5 и более чисел.
В этом случае хотя бы одно из чисел будет равно единице, ведь даже $2⋅5$ уже превышает 8. Как мы доказали выше, ни в каком из таких наборов не может достигаться максимум произведения.
В наборе 4 числа.
Каждое из чисел не меньше 2, значит, единственный возможный вариант это четыре двойки. В этом случае произведение равно 16.
В наборе 3 числа.
Возможны следующие случаи (порядок не важен): ${2,2,4}, {2,3,3}.$ Максимальное произведение достигается во втором случае и равно 18.
В наборе 2 числа.
Возможны следующие случаи (порядок не важен): ${2,6}, {3,5}, {4,4}.$ Максимальное произведение достигается в третьем случае и равно 16.
В наборе 1 число.
Единственный возможный вариант, когда единственное число равно 8.

Теперь будем перебирать возможные значения произведения вниз начиная с наибольшего и проверять, реализуемы ли они в условиях исходной задачи.

Произведение равно 18.
Оно достигается в единственном случае, когда среди первых восьми чисел два числа $a,$ три числа $b$ и три числа $c.$ При этом мы знаем, что среди первых восьми чисел ровно 4 четных. Докажем, что какими бы ни были четности чисел $a,$ $b$ и $c,$ общее количество четных в нашем наборе из восьми не будет равно 4. Разберем несколько случаев:
- Пусть среди $a,b,c$ нет ни одного нечетного, либо все нечетные. Тогда среди наших восьми чисел будет либо 0, либо 8 нечетных, а должно быть ровно 4.
- Пусть среди $a,b,c$ ровно одно нечетное. Если это $a,$ то среди наших восьми чисел будет 2 нечетных. Если $b$ — то 3, если $c$ — тоже 3. Ни в одном из этих вариантов количество нечетных не равно 4.
- Пусть среди $a,b,c$ ровно два нечетных. Если это $a$ и $b,$ то среди наших восьми чисел будет $2+ 3= 5$ нечетных. Если $b$ и $c$ — то 6, если $c$ и $a$ — то 5. Ни в одном из этих вариантов количество нечетных не равно 4.
Получили, что произведение, равное 18, не реализуемо.
Произведение равно 17.
Такое произведение не достигается путем перемножения чисел с суммой 8, так как один из множителей должен быть равен 17.
Произведение равно 16.
Есть пример, где первые 8 членов последовательности равны
$0, 1, 0, 1, 0, 1, 0, 1$
Тогда $k0 = 4,$ $k1 = 4,$ остальные $ki$ равны 0, тогда произведение ненулевых $ki$ равно 16. В полученном примере все условия выполняются, следовательно, 16 — наибольшее достижимое значение произведения.

Ответ:

а) Нет

б) Нет

в) 16

Критерии оценки


Содержание критерия	Балл

Верно получены все перечисленные (см. критерий на 1 балл) результаты	4

Верно получены три из перечисленных (см. критерий на 1 балл) результатов.	3

Верно получены два из перечисленных (см. критерий на 1 балл) результатов.	2

Верно получен один из следующий результатов: — обоснованное решение в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки.	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 6#2023

Иван придумал функцию $f (x )$ , область определения которой $ℝ$ , а область значений – конечное подмножество $ℝ$ .

Настя придумала бесконечную последовательность, в которой каждый член, начиная с пятого, имеет вид

an = f (f(f(an− 4) + an−3) − an−1).

Можно ли с уверенностью утверждать, что начиная с некоторого номера $N$ члены этой последовательности повторяются периодически c некоторым периодом $T > 0$ (т.е. при любых $k ∈ ℕ$ выполнено равенство $aN+k = aN+k+T$ )?

Показать ответ и решение

Заметим, что каждый член последовательности, начиная с пятого, однозначно определяется предыдущими четырьмя членами, следовательно, если в данной последовательности дважды встречается фрагмент $a,b,c,d$ , то есть она имеет вид $a1...,a, b,c,d,...,a,b,c,d,...$ , то она периодическая.

Остаётся показать, что некоторый фрагмент такого вида действительно встретится в последовательности Насти не менее двух раз.

Так как область значений $f (x)$ – конечное множество, то в этом множестве найдётся элемент, который встречается в последовательности бесконечное число раз. Обозначим этот элемент через $a$ .

Так как $a$ встречается бесконечное число раз, а претендентов на роль правого соседа $a$ лишь конечное число, то найдётся число $b$ , такое, что фрагмент $a, b$ встречается в последовательности бесконечное число раз.

Так как фрагмент $a,b$ встречается бесконечное число раз, а претендентов на роль правого соседа фрагмента $a,b$ лишь конечное число, то найдётся число $c$ , такое, что фрагмент $a,b,c$ встречается в последовательности бесконечное число раз.

Аналогично, найдётся число $d$ такое, что фрагмент $a,b,c,d$ встречается в последовательности бесконечное число раз, следовательно, Настина последовательность периодична.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 7#2022

Максим придумал бесконечную последовательность натуральных чисел, в которой каждый член, начиная с третьего, равен последней цифре суммы двух предыдущих членов (в десятичной записи). Можно ли с уверенностью утверждать, что, начиная с некоторого номера $N$ , члены этой последовательности повторяются периодически c некоторым периодом $T > 0$ (т.е. при любых $k ∈ ℕ$ выполнено равенство $aN+k = aN+k+T$ )?

Показать ответ и решение

Заметим, что каждый член последовательности, начиная с третьего, однозначно определяется ровно двумя предыдущими членами последовательности, следовательно, если в данной последовательности дважды встречается фрагмент $a,b$ , то есть она имеет вид $a1...,a,b,...,a,b,...$ , то она периодическая.

Остаётся показать, что некоторый фрагмент такого вида действительно встретится в последовательности Максима не менее двух раз.

Начиная с третьего члена, каждый член последовательности совпадает либо с 0, либо с 1, ..., либо с 9.

Так как последовательность бесконечная, то найдётся член этой последовательности, который повторяется бесконечное число раз.

Пусть $0$ повторяется бесконечное число раз. Тогда следующие после $0$ члены не могут быть всё время разными (их разных – конечное количество, а $0$ встречается бесконечно много раз).

В итоге следующие после $0$ члены также хотя бы раз совпадут, и фрагмент вида $0,b$ действительно встретится в последовательности хотя бы дважды.

Если другое число повторяется бесконечное число раз, то рассуждения в этом случае аналогичны предыдущим.

Таким образом, последовательность Максима периодична.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 8#731

Илья придумал бесконечную последовательность натуральных чисел, в которой каждый член, начиная с сотого, равен последней цифре квадрата предыдущего члена (в десятичной записи). Можно ли с уверенностью утверждать, что, начиная с некоторого номера $N$ , члены этой последовательности повторяются периодически c некоторым периодом $T > 0$ (т.е. при любых $k ∈ ℕ$ выполнено равенство $aN+k = aN+k+T$ )?

Показать ответ и решение

Заметим, что каждый член последовательности, начиная с сотого, однозначно определяется единственным предыдущим ему членом последовательности, следовательно, если в данной последовательности, начиная с сотого члена, дважды встречается одно и то же число, то она периодическая.

Остаётся показать, что некоторое число такого вида действительно встретится в последовательности Ильи не менее двух раз, начиная с сотого члена.

Начиная с сотого члена, каждый член последовательности совпадает либо с 0, либо с 1, ..., либо с 9.

Так как последовательность бесконечная, то найдётся член этой последовательности, который повторяется бесконечное число раз. Таким образом, последовательность Ильи периодична.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 9#729

Илья выписал последовательность остатков от деления последовательно идущих натуральных чисел на 3 (начиная с некоторого числа). Верно ли, что начиная с некоторого номера $N$ , члены последовательности повторяются периодически c некоторым периодом $T > 0$ (т.е. при любых $k ∈ ℕ$ выполнено равенство $aN+k = aN+k+T$ )?

Показать ответ и решение

Любое $a ∈ ℕ$ имеет такой же остаток от деления на 3, что и $a + 3t$ , где $t ∈ ℕ$ – произвольное.

Так как различных остатков от деления на 3 может быть не больше 3, то фрагмент последовательности, в котором нет одинаковых чисел, имеет длину не больше 3: $b1,b2,b3$ , но тогда $b4 = b1$ , $b5 = b2$ , $b6 = b3$ и т.д., то есть члены выписанной Ильёй последовательности, начиная с некоторого номера, повторяются периодически.

Ответ: Да

Ошибка.
Попробуйте повторить позже

Задача 10#732

Тимур придумал бесконечную последовательность действительных чисел, в которой первые 10 членов натуральные числа, а каждый член, начиная с третьего, равен остатку от деления предпредыдущего члена на предыдущий член, либо $0$ (то есть, например, $a3$ равен остатку от деления $a1$ на $a2$ , либо $a3 = 0$ ).

а) Приведите пример такой последовательности.

б) Назовём периодом последовательности наименьшее натуральное число $T$ , такое что, начиная с некоторого номера $N$ , для любого $k ∈ ℕ ∪ {0}$ выполняется $aN+k = aN+k+T$ . Найдите период последовательности Тимура.

Показать ответ и решение

а) Будем искать такую последовательность в виде

A, A + B, A, B,A − B, 2B − A, 2A − 3B, 5B − 3A, 5A − 8B, 13B − 8A, ...

(каждый последующий член равен разности двух предыдущих). Чтобы такая последовательность подходила под условие, необходимо и достаточно, чтобы

{ A > B > A − B > 2B − A > 2A − 3B > 5B − 3A > 5A − 8B > 13B − 8A > 0 A, B ∈ ℕ.

Данная система эквивалентна системе

( ( { 21 13 { 336 338 --B < A < --B ----B < A < ---B ( 13 8 ⇔ ( 208 208 A, B ∈ ℕ. A, B ∈ ℕ.

Таким образом, можно взять, например, $A = 337$ , $B = 208$ . При этом получим последовательность

337,545,337, 208,129,79, 50,29,21,8, ...

б) Если какой-то из членов последовательности равен $0$ , то, начиная с него, все члены последовательности равны $0$ (так как результат деления на $0$ не может совпасть ни с каким действительным числом).

Пусть никакой из членов последовательности не равен $0$ .

1) Пусть $a1 > a2$ . Так как остаток от деления не может быть больше делителя, то $a2 > a3 > a4 > ...$ , то есть последовательность убывает.

При этом остатки от деления натуральных чисел будут натуральными числами ( $0$ мы запретили), то есть каждый следующий член последовательности будет натуральным числом, меньшим предыдущего по крайней мере на $1$ .

Тогда член последовательности с номером $N = a 1$ должен быть натуральным числом, меньшим, чем $a1$ по крайней мере на $N = a1$ , что невозможно.

2) Пусть $a2 > a1$ , тогда $a3 = a1$ и этот пункт сводится к пункту 1) при помощи смены обозначений $a2 = b1$ , $a3 = b2$ , ..., $an+1 = bn$ и дословного повторения рассуждения для последовательности $b ,...,b ,... 1 n$ .

Таким образом, последовательностей, подходящих под условие, у которых никакой из членов не равен $0$ , не бывает. Тогда, начиная с некоторого номера, все члены последовательности Тимура равны $0$ и, значит, $T = 1$ .

Ответ:

а) $337,545, 337,208,129, 79,50,29, 21,8,...$

б) $1$

Ошибка.
Попробуйте повторить позже

Задача 11#12710

По кругу выписаны несколько целых чисел, причем каждое из чисел больше суммы двух предыдущих, если двигаться по часовой стрелке. Например, если выписаны три числа $a1,$ $a2$ и $a3$ (нумерация по часовой стрелке), то должны выполняться три неравенства: $a1+ a2 < a3,$ $a2+ a3 < a1$ и $a3+ a1 < a2.$

а) Может ли количество чисел равняться 10?

б) Могут ли два неотрицательных числа стоять рядом, если выписано не менее 4 чисел?

в) Какое наименьшее количество отрицательных чисел могло быть выписано, если всего чисел 100?

Показать ответ и решение

а) Да, может, например, так:

$PIC$

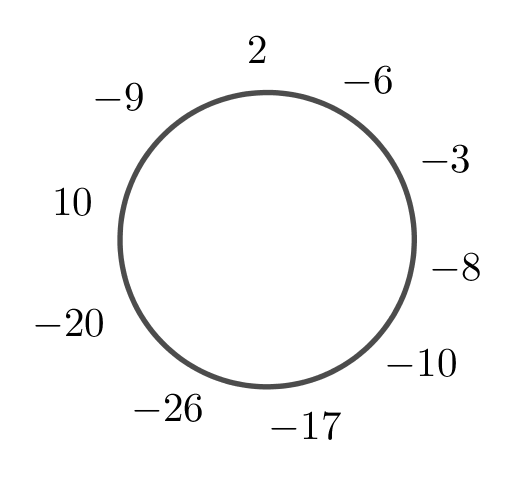
б) Обозначим через $n$ общее количество чисел в круге. Пусть, не умаляя общности, $a1$ и $a2$ — два соседних неотрицательных числа. Следующее за ними по часовой стрелке число $a3$ по условию должно быть больше суммы $a1+ a2,$ а значит, больше каждого из $a1$ и $a2.$ Будем двигаться далее по часовой стрелке, проводя аналогичное рассуждение (нам ничто не помешает, так как $a2$ и $a3$ снова неотрицательные). Получим, что при движении по часовой стрелке начиная с $a3$ числа строго увеличиваются, причем $a3 > a1$ и $a3 > a2,$ следовательно, $an > a3 > a1.$ Однако по условию $a1$ должно быть больше суммы $an−1+ an,$ что невозможно при $an >a1$ и неотрицательном $an−1.$ Значит, два неотрицательных числа не могли стоять рядом.

в) В предыдущем пункте мы доказали, что неотрицательные числа не могут соседствовать в круге, следовательно, отрицательных чисел должно быть не меньше половины от общего количества, то есть не меньше 50.

Допустим отрицательных ровно 50, тогда неотрицательных тоже 50, и они должны чередоваться в круге. Обозначим числа $a ,...,a 1 n$ по часовой стрелке, не умаляя общности, будем считать, что $a 1$ отрицательное. Тогда из чередования мы знаем, что $a2$ неотрицательное. По условию должно выполняться $a3 > a1+ a2,$ следовательно, $a3$ — отрицательное число, большее, чем $a1.$ Аналогично получаем (нам ничто не помешает, так как важна только отрицательность/неотрицательность числа, а она при сдвиге на 2 по часовой стрелке сохраняется), что $a5 > a3, ..., a99 > a97,$ а также $a1 > a99.$ Получаем противоречивую цепочку неравенств

a < a < ⋅⋅⋅< a < a 1 3 99 1

Значит, 50 отрицательных быть не могло. На 51 отрицательное число строится следующий пример:

$PIC$

Ответ:

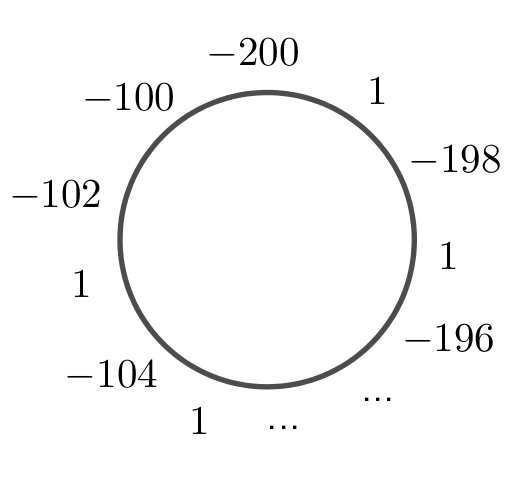
а) Да

б) Нет

в) 51

Критерии оценки


Содержание критерия	Балл

Верно получены все перечисленные (см. критерий на 1 балл) результаты	4

Верно получены три из перечисленных (см. критерий на 1 балл) результатов.	3

Верно получены два из перечисленных (см. критерий на 1 балл) результатов.	2

Верно получен один из следующий результатов: — пример в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки.	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 12#11754

На доску слева направо в ряд выписали пять натуральных чисел. Затем между каждой парой соседних чисел $ai$ и $ai+1$ записали разность $ai+1− ai.$ Оказалось, что каждая из разностей, кроме самой левой, ровно на единицу больше той разности, которая записана слева от нее, то есть $ai+1 − ai$ на единицу больше, чем $ai− ai−1$ . Например, для исходных чисел 4, 6, 9, 13, 18 разности соседей равны 2, 3, 4, 5 — каждая следующая на единицу больше предыдущей.

а) Может ли сумма пяти чисел, записанных изначально, равняться 300?

б) Может ли сумма пяти чисел, записанных изначально, равняться 426?

в) Найти наибольшее возможное значение самого правого из чисел, записанных изначально, если их сумма равна 100.

Показать ответ и решение

Пусть на доску выписали числа $a1,$ $a2,$ $a3,$ $a4$ и $a5$ в таком порядке. Пусть $a2− a1 = r.$

По условию имеем:

$pict$

Тогда

$pict$

В задаче нас просят выяснить может ли сумма чисел равнятся 300 и 426, выразим её через $a1$ и $r :$

a5 +a4+ a3+ a2+ a1 = a1+ 4r+ 6+ a1+ 3r+ +3 + a1+ 2r+ 1+ a1+ r+ a1 = 5a1 +10r+ 10

а) Мы выяснили, что $a1+ a2+ a3 +a4 +a5 = 5a1+ 10r+ 10.$ Значит,

5a1+10r+ 10= 300 ⇒ a1+ 2r+ 2= 60 ⇒ a1 = 60− 2r− 2 = 2(29− r)

Тогда, чтобы число $a1$ было натуральным, нужно взять $r <29.$ Пусть $r =28.$ Тогда $a1 = 2(29 − 28)= 2.$ То есть

$pict$

Разности по построению чисел удовлетворяют условию, проверим сумму:

a1+ a2+ a3+ a4+ a5 = 2+ 30+ 59+ 89+ 120 = 300

Значит, изначально могли быть написаны числа 2, 30, 59, 89 и 120.

б) Если сумма чисел $a1,$ $a2,$ $a3,$ $a4$ и $a5$ представима в виде

a5 +a4+ a3+ a2+ a1 = 5a1+ 10r+ 10,

значит она кратна 5, так как каждое слагаемое кратно 5. 426 не делится на 5, поэтому сумма пяти чисел, записанных изначально, не может равнятся 426.

в) В этом пункте нас просят найти наибольшее значение самого правого числа. Мы знаем, что $a5 = a1+ 4r+ 6.$

Если сумма чисел $a1,$ $a2,$ $a3,$ $a4$ и $a5$ равна 100, то

5a1+ 10r+ 10= 100 ⇒ a1+ 2r+ 2= 20 ⇒ a1 = 2(9 − r)

Так как $a1$ — натуральное число, $r < 9.$ Тогда мы можем оценить $a5 :$

a5 = a1+ 4r+ 6= 2(9 − r)+ 4r+ 6= 18− 2r+ 4r+ 6= 24+ 2r ⇒

⇒ a5 = 24 +2r < 24 +2 ⋅9= 24+ 18= 42

Заметим, что $a5 = 24+ 2r$ кратно 2 и $a5 < 42.$ Значит, наибольшее возможное значение $a5 = 40.$

Докажем, что значение $a5 = 40$ достигается. Для этого простроим пример, подходящий под условие, в котором $a5 = 40.$ Если $a5 = 24+ 2r = 40,$ то $r = 8.$ Значит,

a1 = 2(9− r)= 2(9 − 8)= 2

Тогда

$pict$

Найдем сумму полученных чисел:

a1+a2 +a3+ a4+ a5 = 2+ 10+ 19+ 29+ 40= 100

Значит, полученный пример удовлетворяет условию. Тогда наибольшее возможное значение самого правого из чисел, записанных изначально, если их сумма равна 100, равно 40.

Ответ:

а) да

б) нет

в) 40

Ошибка.
Попробуйте повторить позже

Задача 13#11684

Последовательность чисел устроена следующим образом: первый ее член равен нулю, а каждый следующий отличается от предыдущего на единицу.

а) Может ли 22й член последовательности быть равен нулю?

б) Может ли среди первых 11 членов последовательности быть ровно шесть двоек?

в) Для каждого целого числа $i$ определим $ki$ — количество чисел, равных $i,$ среди первых восьми членов последовательности. Какое наибольшее значение может принимать произведение всех ненулевых $ki?$ Например, если среди первых восьми членов последовательности три нуля, одна двойка и четыре единицы, то $k0 =3,$ $k1 = 4,$ $k2 = 1,$ остальные равны нулю. Произведение ненулевых $ki$ в этом случае равно $3⋅4 ⋅1 = 12.$

Показать ответ и решение

а) Любые два соседних члена последовательности отличаются на 1, следовательно, они разной четности. Первый член 0 — четный, четность чередуется, значит, все члены с нечетными номерами четны, а с четными номерами — нечетны. Таким образом, 22-ой член последовательности должен быть нечетным и не может быть равен нулю.

б) Среди первых 11 членов последовательности ровно 6 четных (это те, у которых нечетные индексы: 1, 3, 5, 7, 9, 11). При этом мы знаем, что первый четный член равен нулю. Получаем противоречие, так как шесть двоек невозможно разместить на пяти свободных позициях для четных чисел.

в) Рассмотрим ненулевые $ki.$ Их сумма должна равняться 8, так как они равны количествам вхождений различных чисел в первую восьмерку.

Решим сначала другую задачу. Найдем максимально возможное значение, которое может принимать произведение нескольких натуральных чисел, сумма которых равна 8, а уже затем разберемся, какое наибольшее значение произведения реализуемо в условиях нашей задачи.

Пусть среди наших чисел с суммой 8 есть хотя бы одна единица, а их произведение равно $p,$ то есть имеется следующий набор чисел: $1,a1,...,ak.$ Тогда, если мы возьмем набор $a1+ 1,...,ak,$ то сумма чисел в нем будет также равна 8, а произведение будет больше, чем в исходном. Таким образом, можем сделать вывод, что максимум произведения не может достигаться в наборе, в котором есть хотя бы одна единица.

Рассмотрим всевозможные наборы чисел с суммой 8, такие, что ни одно из чисел не равно единице, чтобы найти максимум произведения чисел в таком наборе. Рассмотрим, чему может равняться количество чисел в наборе.

В наборе 5 и более чисел.
В этом случае хотя бы одно из чисел будет равно единице, ведь даже $2⋅5$ уже превышает 8. Как мы доказали выше, ни в каком из таких наборов не может достигаться максимум произведения.
В наборе 4 числа.
Каждое из чисел не меньше 2, значит, единственный возможный вариант это четыре двойки. В этом случае произведение равно 16.
В наборе 3 числа.
Возможны следующие случаи (порядок не важен): ${2,2,4}, {2,3,3}.$ Максимальное произведение достигается во втором случае и равно 18.
В наборе 2 числа.
Возможны следующие случаи (порядок не важен): ${2,6}, {3,5}, {4,4}.$ Максимальное произведение достигается в третьем случае и равно 16.
В наборе 1 число.
Единственный возможный вариант, когда единственное число равно 8.

Теперь будем перебирать возможные значения произведения вниз начиная с наибольшего и проверять, реализуемы ли они в условиях исходной задачи.

Произведение равно 18.
Оно достигается в единственном случае, когда среди первых восьми чисел два числа $a,$ три числа $b$ и три числа $c.$ При этом мы знаем, что среди первых восьми чисел ровно 4 четных. Докажем, что какими бы ни были четности чисел $a,$ $b$ и $c,$ общее количество четных в нашем наборе из восьми не будет равно 4. Разберем несколько случаев:
- Пусть среди $a,b,c$ нет ни одного нечетного, либо все нечетные. Тогда среди наших восьми чисел будет либо 0, либо 8 нечетных, а должно быть ровно 4.
- Пусть среди $a,b,c$ ровно одно нечетное. Если это $a,$ то среди наших восьми чисел будет 2 нечетных. Если $b$ — то 3, если $c$ — тоже 3. Ни в одном из этих вариантов количество нечетных не равно 4.
- Пусть среди $a,b,c$ ровно два нечетных. Если это $a$ и $b,$ то среди наших восьми чисел будет $2 + 3= 5$ нечетных. Если $b$ и $c$ — то 6, если $c$ и $a$ — то 5. Ни в одном из этих вариантов количество нечетных не равно 4.
Получили, что произведение, равное 18, не реализуемо.
Произведение равно 17.
Такое произведение не достигается путем перемножения чисел с суммой 8, так как один из множителей должен быть равен 17.
Произведение равно 16.
Есть пример, первые 8 членов последовательности равны: 0, 1, 0, 1, 0, 1, 0, 1. Тогда $k0 = 4,$ $k1 = 4,$ остальные $ki$ равны 0, тогда произведение ненулевых $ki$ равно 16. В полученном примере все условия выполняются, следовательно, 16 — наибольшее достижимое значение произведения.

Ответ:

а) Нет

б) Нет

в) 16