Ошибка.
Попробуйте повторить позже
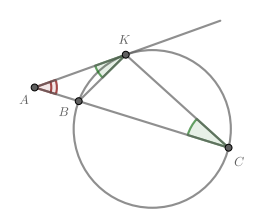
Параллелограмм и окружность расположены так, что сторона
касается окружности,
является
хордой, а стороны
и
пересекают окружность в точках
и
соответственно.
а) Докажите, что около четырехугольника можно описать окружность.
б) Найдите длину отрезка если известно, что
.
(пробный ЕГЭ 2017)
а) Четырехугольник вписанный
.
, т.к.
— параллелограмм.
—
вписанный.
![]()
б) Для начала докажем лемму.
___________________________________________________________
Лемма 1. Пусть есть окружность и точка вне ее. Через точку
проведена касательная
к окружности,
а также прямая, пересекающая окружность в двух точках
и
. Тогда
.
Доказательство. , т.к. угол между касательной и хордой равен вписанному углу, опирающемуся
на эту хорду. Тогда
по двум углам (т.к.
общий). Запишем подобие
|
|
___________________________________________________________
Вернемся к решению исходной задачи. Дважды воспользовавшись Леммой 1 для точек и
, получим
соотношения
Далее, из равенств углов, доказанных в первом пункте, очевидно, что трапеции и
— равнобокие, то
есть
. Пусть
. Тогда из вписанности четырехугольника
|
|
Выразим двумя способами по теореме косинусов для треугольников
и
и найдем
Найдем по теореме косинусов для треугольника
![]()
б)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




