Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система неравенств
имеет конечное число решений.
Первое неравенство можно переписать в виде
Заметим, что прямые и
симметричны относительно прямой
, следовательно, имеют равные углы между осями
абсцисс и ординат соответственно. Таким образом, первое неравенство задает некоторую область, обозначенную на рисунке голубым
цветом.
Второе неравенство при задает пустое множество, но тогда и вся система не имеет решений, что нам не подходит. при
оно
задает точку
, удовлетворяющую первому неравенству, то есть система имеет одно решение, что нам подходит. При
фиксированном
оно задает круг с центром в точке
(центр движется по прямой
) и радиусом
.
При изменении
от
до
окружность движется вниз по прямой
и ее радиус увеличивается от
до
.
На рисунке обозначено положение круга, при котором он с голубой областью имеет конечное число решений (касается границы этой области, и при этом касании мы имеем два решения):
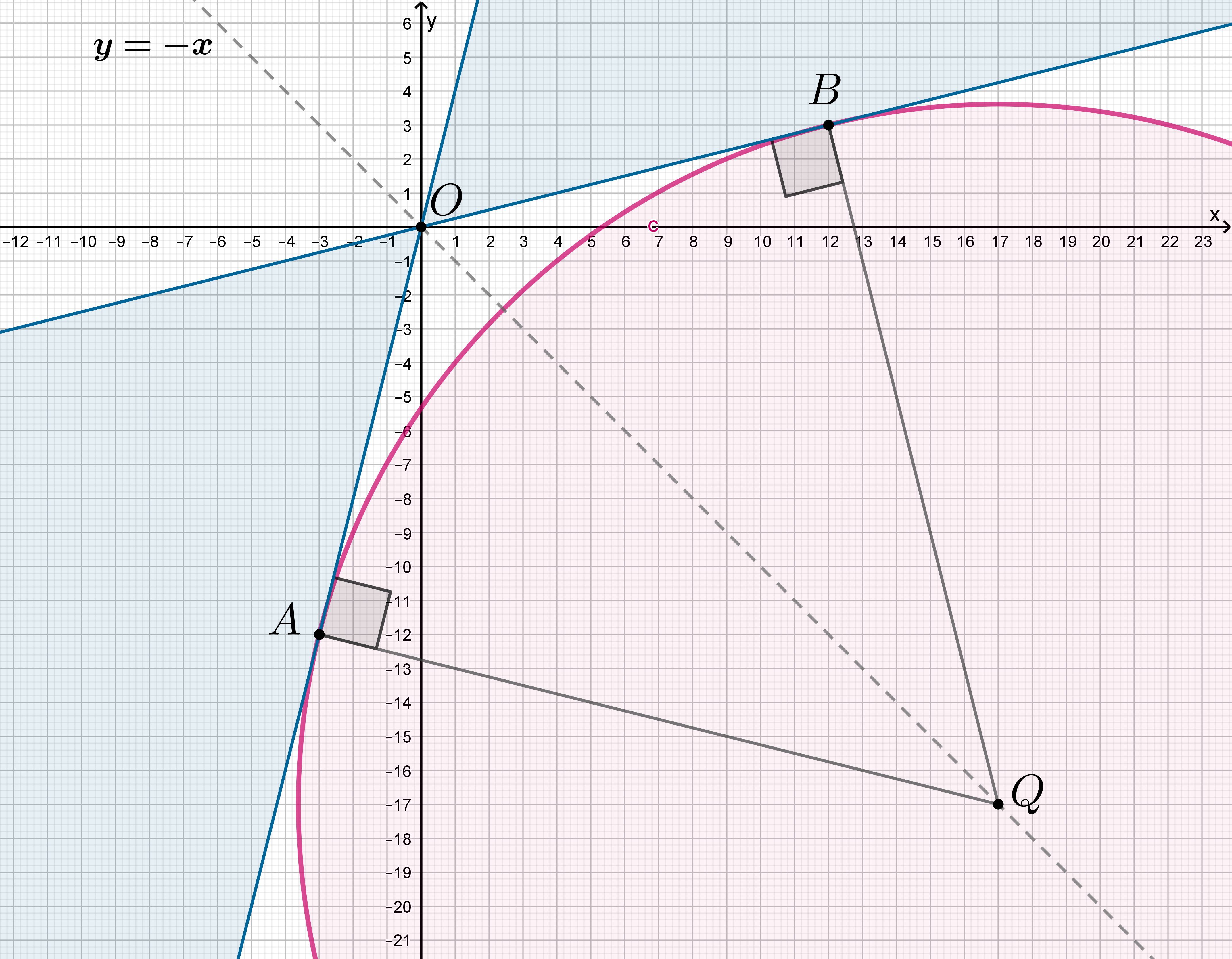
Заметим, что в силу симметрии прямых и
относительно прямой
, а также симметрии круга
относительно этой прямой, круг, касаясь одной прямой, будет касаться также и другой прямой.
Если окружность касается прямой, то радиус окружности равен расстоянию от центра окружности до этой прямой:
Таким образом, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет ровно два решения.
В первом уравнении системы оба слагаемых левой части неотрицательны при всех значениях и
Сумма этих
слагаемых равна нулю тогда и только тогда, когда каждое из них равно нулю. Таким образом, исходная система
равносильна
В первом уравнении преобразованной системы имеем стандартную параболу во втором — линейную функцию
Линейная и квадратичная функции имеют не более двух точек пересечения, а по условию нас просят найти
при которых решений ровно два. Значит, нас интересуют значения
при которых обе эти точки пересечения являются
решениями системы.
Условие означает, что никакие точки вертикальной прямой
не могут быть решениями системы.
Четвертое условие означает, что нас интересуют только положительные значения
Последнее условие задает область между вертикальными прямыми
и
(включая эти прямые, так
как знаки нестрогие).
Таким образом, чтобы система имела ровно два решения, обе точки пересечения функций и
должны лежать в области
причем ни одна из них не должна принадлежать «запрещенной» вертикальной прямой
Построим графики (на
картинке область
изображена при
):
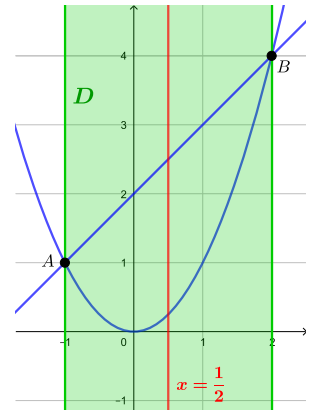
Графики и
пересекаются в точках
и
Ни одна из них не лежит на прямой
- При
левая граница
области
обращается в
и проходит через точку
а правая граница
области
обращается в
и проходит через точку
то есть обе точки принадлежат области
такие
нам подходят.
- При всех
область
становится «уже» и точка
оказывается левее прямой
а точка
— правее прямой
то есть точки
и
не попадают в область
такие
нам не подходят.
- При всех
обе точки
и
лежат внутри области
Таким образом, нам подходят
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточно обоснованное построение/недостаточно обоснован какой-то момент при исследовании | 3 |
| ИЛИ | |
| ответ отличается от верного невключением граничной точки | |
| Верно найдены точки пересечения и граничное значение параметра, но переход к ответу неверный | 2 |
| ИЛИ | |
| допущена вычислительная ошибка | |
| Верно сведено к исследованию графически или аналитически и выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все , при которых система неравенств
имеет решения.
Первое неравенство при задает точку
не удовлетворяющую второму неравенству, следовательно, этот случай нам не подходит.
При
первое неравенство равносильно
Оно задает круг с центром в (который движется по прямой
) и радиусом
Заметим, что при отдалении
круга от начала координат его радиус увеличивается.
Второе неравенство задает область под прямой Заметим, что эта прямая параллельна траектории движения центра
круга. Также заметим, что при
и
круги симметричны относительно прямой
Следовательно, если нам подходит
то нам подходит также и
Рассмотрим только Тогда граничное положение круга, при котором он имеет хотя бы одну общую точку с голубой областью —
когда круг касается прямой
На рисунке это положение
при этом положение
— ему симметричное при противоположном

Тогда расстояние от центра круга до прямой
равно радиусу круга:
Следовательно, при и
система имеет хотя бы одно решение.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых среди решений
системы неравенств
нет решений, у которых , в то же время имеет хотя бы одно решение
, у которого
.
Первое неравенство равносильно
Первая система в нижней полуплоскости (с границей ) задает вертикальную полосу между прямыми
и
.
Вторая система в верхней полуплоскости задает круг с центром в начале координат и радиусом
, если
;
точку, совпадающую с началом координат, если
(не подходит, так как в этом случае начало координат не лежит в
области, задающейся вторым неравенством). Назовем область, задающуюся первым неравенством,
, и обозначим голубым
цветом.
Пусть далее .
Второе неравенство задает розовую область над прямой (назовем ее
).
Чтобы эти области пересекались, и в пересении была хотя бы одна точка , у которой
и точно
, граница розовой
области должна находиться между прямыми
и
.
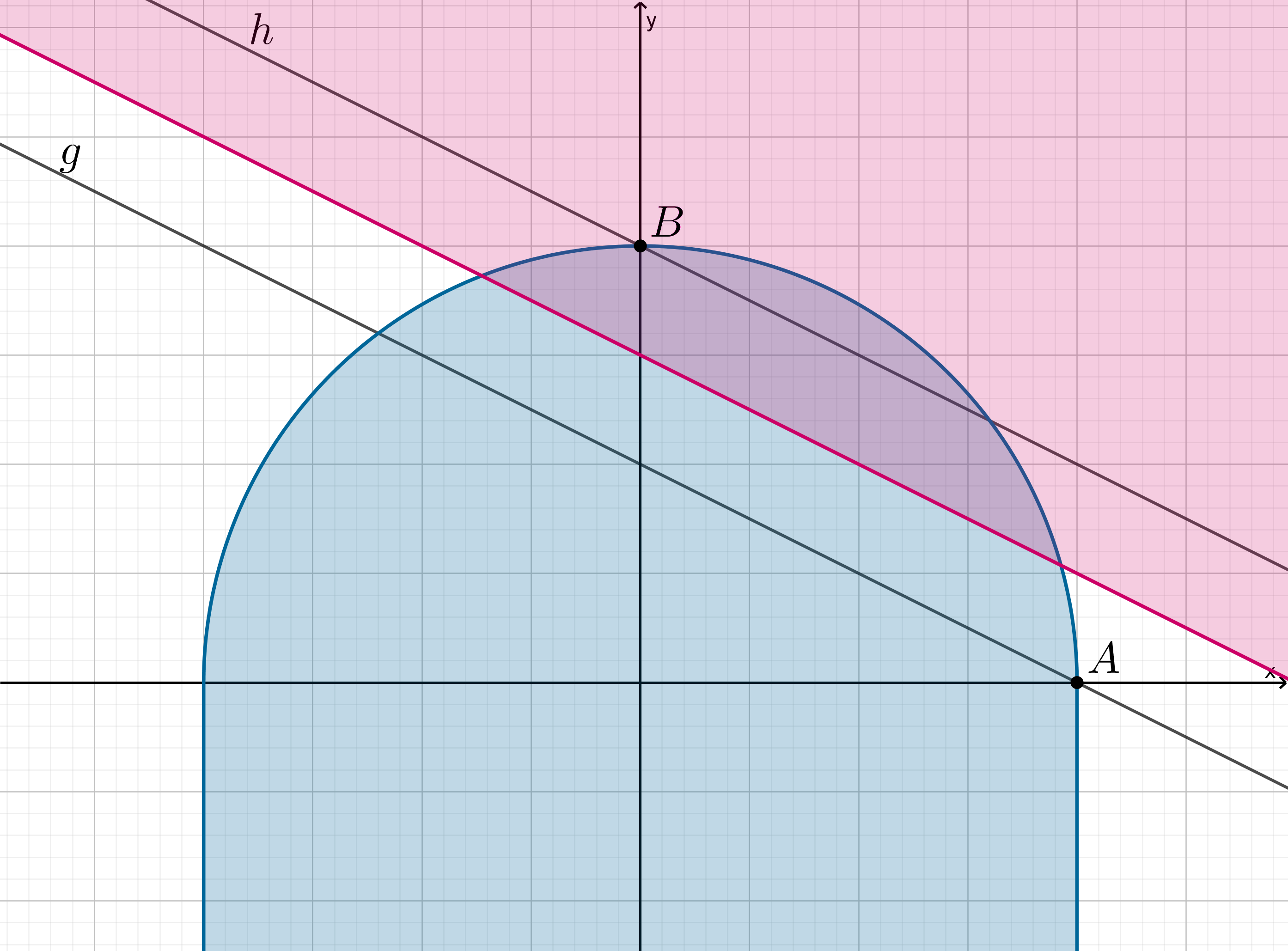
Точка имеет координаты
, точка
имеет координаты
, следовательно,
Следовательно, , то есть
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Неравенство равносильно
Следовательно, оно задает полосу между прямыми и
.
Уравнение при задает пустое множество, следовательно, система не имеет решений, что нам не подходит. При
оно
задает точку
, которая лежит в полосе (так как удовлетворяет неравенству), следовательно,
нам подходит. При
уравнение задает окружность с центром в
, который движется по прямой
, и радиусом
,
который при движении ентра по прямой
сверху вниз увеличивается.
Единственное решение у системы тогда, когда окружность касается границы полосы внешним образом (в точке ):
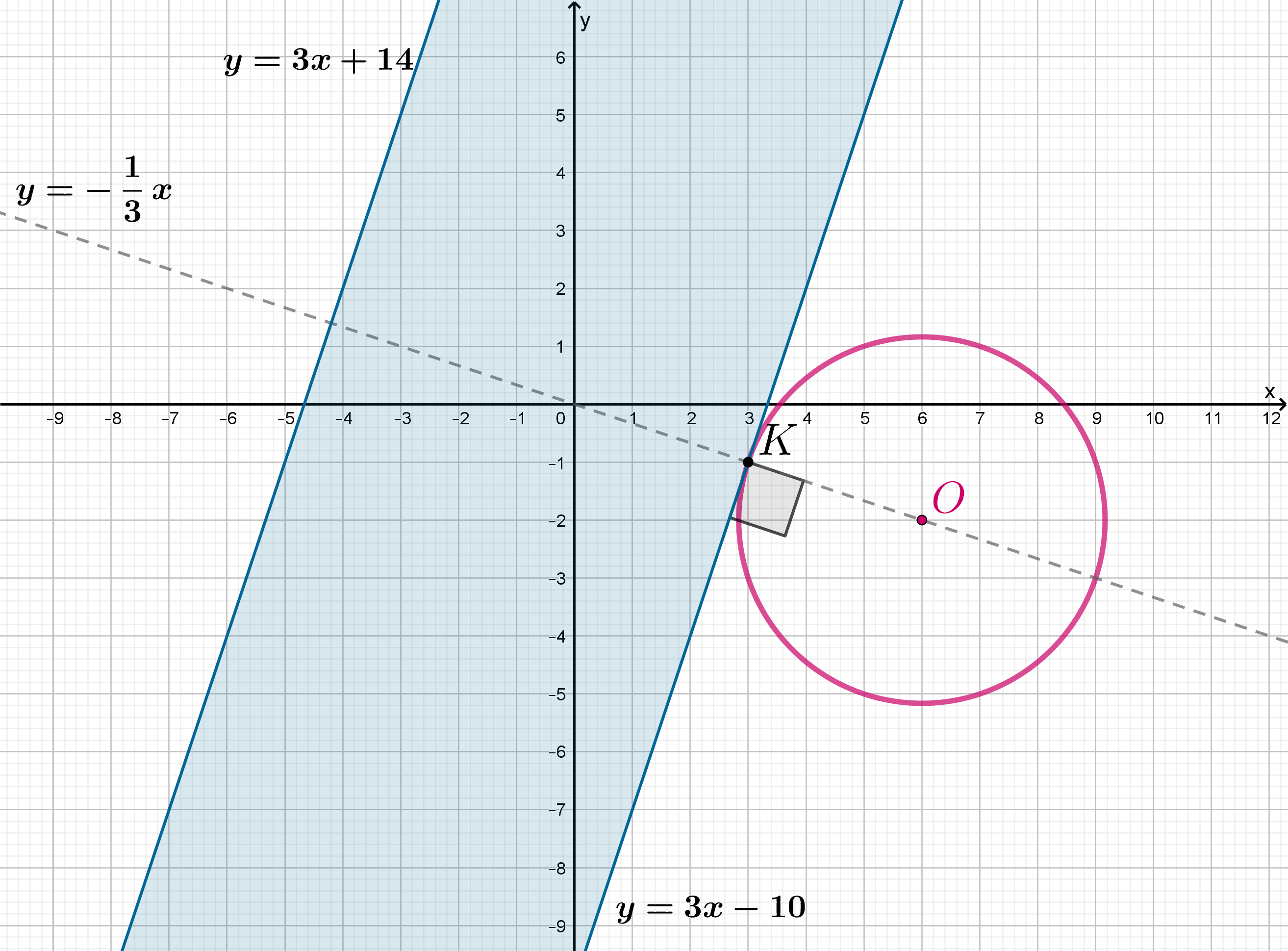
Заметим, что точка касания лежит на прямой , так как произведение коэффициентов прямых
и
равно
, следовательно, прямые перпендикулярны.
Следовательно, координаты точки можно найти как координаты точки пересечения
и
:
Таким образом, :
Значит, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система
имеет единственное решение.
1) Преобразуем неравенство системы:
Т.к. сумма квадратов всегда неотрицательна, то данная совокупность равносильна:
Т.к. равносильно
или
, то данная совокупность задает область,
состоящую из части плоскости, находящейся не ниже прямой
, из части плоскости,
находящейся не выше прямой
, а также из точки
:
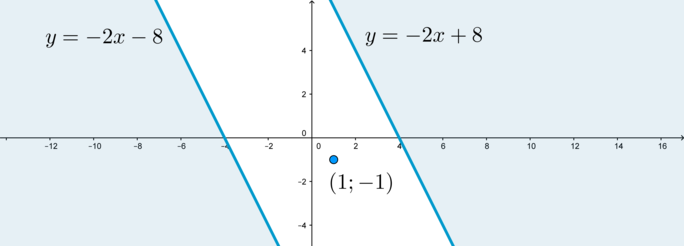
2) Преобразуем уравнение системы:
Данное уравнение при задает окружность с центром в точке
и радиусом
; при
задает точку
; при
– пустое множество.
Т.к. точка не попадает в область, заданную неравенством, то при
система точно не
будет иметь решений.
3) Рассмотрим случай .
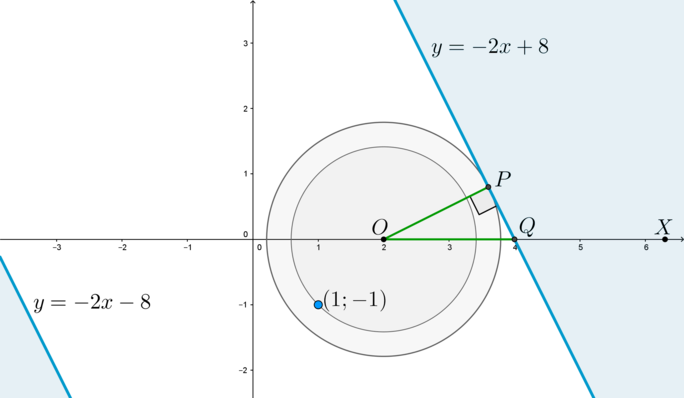
Система будет иметь единственное решение тогда и только тогда, когда окружность будет иметь ровно одну общую точку с областью. Это возможно в одном из двух случаев:
(1) Если окружность коснется границы области .
Пусть – точка касания (то есть
). Рассмотрим прямоугольный
, где
– точка пересечения прямой
с осью абсцисс.
Т.к. угловой коэффициент прямой равен
, то
, следовательно,
. Тогда
Т.к. и есть радиус окружности, то
(2) Если окружность проходит через точку .
Это значит, что расстояние между точками и
равно радиусу окружности, следовательно,


