Ошибка.
Попробуйте повторить позже
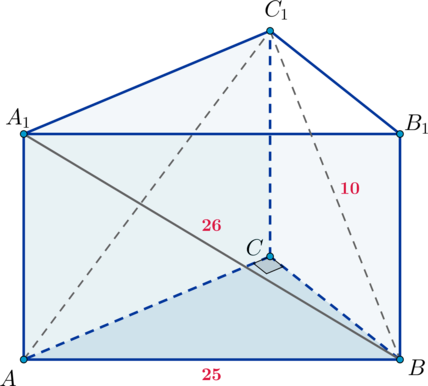
Основанием прямой треугольной призмы является прямоугольный треугольник
причем
Диагонали
боковых граней
и
равны 26 и 10 соответственно,
а) Докажите, что — прямоугольный.
б) Найдите объем пирамиды
а) Так как
то по теореме о трех перпендикулярах
Следовательно,
—
прямоугольный.
б) Заметим, что и
следовательно, по признаку перпендикулярности прямой и плоскости
Следовательно,
— высота пирамиды
с основанием
Так как — прямоугольный, то
По теореме Пифагора имеем:
Тогда искомый объем равен

б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Мало кто знает, но в своё время Дед Мороз тоже закончил мехмат МГУ — Мурманского Государственного Университета! В ту эпоху ЕГЭ ещё не было и для поступления Дед Мороз сдавал внутренние вступительные экзамены.
Дан куб в который вписан шар с центром в точке
На
диагонали
отмечена точка M так, что
Точка
—
середина диагонали
а) Докажите, что центр шара принадлежит плоскости
б) Из точек и
опустили перпендикуляры
и
на плоскость
Найдите объём пирамиды
если ребро куба равно
8.
Попробуйте решить оба пункта, и кто знает, возможно, и вы однажды станете студентом МГУ!!!
а)
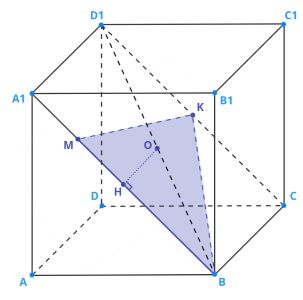
1. Шар вписан в куб, центром этих фигур является одна и та же точка, поэтому работать будем именно с центром куба. Центр куба — точка пересечения его диагоналей.
2. Пусть — середина диагонали
Теперь следует доказать, что точка
принадлежит плоскости
3. Диагональ лежит в плоскости
В этой же плоскости лежат и
три точки плоскости
то есть точка
лежит в той же плоскости, что и
все точки
Ч.Т.Д.
б)
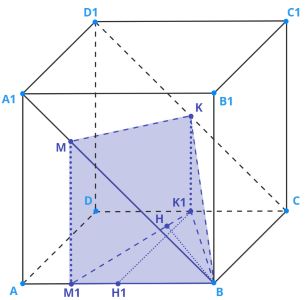
1. Проведём перпендикуляр к прямой
2. следовательно,
перпендикулярно любой прямой,
лежащей в плоскости
то есть
3. и
означают, что
То есть
— высота пирамиды. Найдем её длину через метод площадей для
4. Проведём перпендикуляр к
Его длина равна длине стороны
так как
— прямоугольник.
5. Из подобия , получаем
откуда поскольку
— куб, у него все
рёбра равны.
6. Аналогично находим, что откуда
и
— середины
сторон
и
соответственно.
7. По теореме Пифагора для
8. По методу площадей для вычислим высоту
9. Основание пирамиды — четырёхугольник Прямые
и
перпендикулярны плоскости
значит они параллельны и
на самом деле — трапеция.
10. Из тезисов и
выводим, что
То есть
— высота трапеции.
11. Найдём площадь основания пирамиды:
12. Найдём объём пирамиды:
Ошибка.
Попробуйте повторить позже
Точки и
— середины рёбер
и
соответственно куба
а точка
расположена на ребре
причём
Плоскость
проходит через точку
перпендикулярно прямой
а) Докажите, что плоскость делит ребро
в отношении
считая от
б) Найдите отношение объёмов многогранников, на которые куб разбивается плоскостью
а) Рассмотрим прямоугольник в плоскости
В нём
— это средняя линия, значит,
Отсюда
так как
по условию.
В плоскости грани проведём через точку
прямую, перпендикулярную
Пусть она пересекает сторону
в точке
то есть
Заметим, что
как диагонали квадрата, следовательно,
Рассмотрим треугольники
и
Они подобны, так как
значит,
![]()
В кубе ребро
перпендикулярно грани
значит,
Через точки
и
в
плоскостях
и
соответственно проведем прямые
и
параллельные
Точки
и
лежат на
и
соответственно. Тогда
Плоскость образована прямыми
и
которые перпендикулярны прямой
значит,
Тогда
— это плоскость
Точка
значит, искомое отношение равно
б) Рассмотрим многогранник отсечённый от куба плоскостью
Он является прямой призмой с
основанием
и высотой
так как треугольник
лежит в плоскости
а
и
![]()
Пусть длина каждого ребра куба равна Тогда, так как
то отрезки
Поскольку
прямоугольный, то имеем:
Объём всего куба равен тогда имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Найдите объем прямоугольного параллелепипеда, диагональ которого равна и образует с двумя смежными гранями
углы
и
соответственно.
Будем считать, что — длина диагонали
,
— это угол между диагональю и гранью
, а
— угол
между диагональю и гранью
.
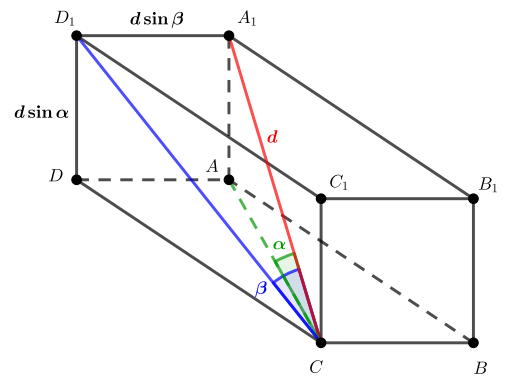
Известно, что угол между прямой и плоскостью равен углу между прямой и ее проекцией на эту плоскость. Также
мы знаем, что проекциями диагонали на грани в прямоугольном параллелепипеде являются соответствующие
диагонали граней. Из этого получаем, что .
— прямоугольный с прямым углом
,
— прямоугольный с прямым углом
, кроме того,
— прямоугольник и
, тогда
По теореме Пифагора для треугольника
|
CD = |
Итого, объем параллелепипеда равен
|
V = DA ⋅ DD1 ⋅ DC = dsinβ ⋅ dsinα ⋅ d |
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде с основанием
на медиане
основания
взята точка
так, что
Через точку
проведена плоскость
которая перпендикулярна прямой
и пересекает
боковые ребра
и
в точках
и
соответственно.
а) Докажите, что
б) Найдите объем пирамиды, вершиной которой является точка а
основанием — сечение пирамиды
плоскостью
если известно, что
а) Пусть — высота пирамиды,
— точка пересечения медиан.
Следовательно,
Так как по условию то можно обозначить
Тогда
Следовательно,
Так как перпендикулярна плоскости
то нужно построить две
пересекающиеся прямые в плоскости
которым
будет перпендикулярна.
Первая прямая: так как то проведем через точку
прямую
Тогда
Вторая прямая: так как то
Следовательно, проведем
тогда
Следовательно, проходит через точки
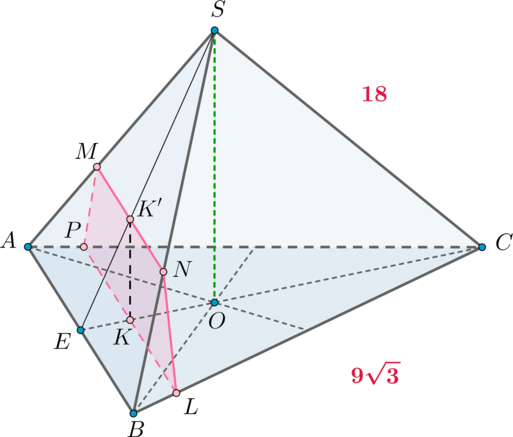
Заметим, что пересечет плоскость
по прямой, параллельной
(в
противном случае
будет иметь общую точку с
что невозможно, так как
Следовательно, и проходит через
Из подобия
Из подобия
б) Рассмотрим пирамиду
— высота этой пирамиды,
—
трапеция
Следовательно,
Так как то
Следовательно,
Из подобия
Из пункта а) Из подобия
Следовательно,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана пирамида с вершиной
, высота которой падает в точку пересечения биссектрис
основания, являющегося равнобедренным треугольником с
. Известно, что радиус вписанной
в треугольник
окружности равен
,
,
. Найдите объем пирамиды.
1) 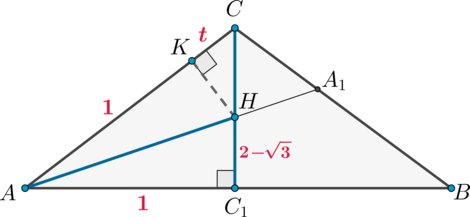
Пусть – высота пирамиды, то есть
– точка пересечения биссектрис основания. Рассмотрим
основание
. Так как центр вписанной в треугольник окружности лежит на пересечении
биссектрис, то
– центр вписанной окружности. Пусть
– биссектрисы, тогда
также
медиана и высота, так как
. Следовательно,
, следовательно,
и есть
радиус вписанной окружности.
Проведем . Тогда
. Пусть
. Тогда
.
Тогда из подобия
:
Значит, площадь основания
2) 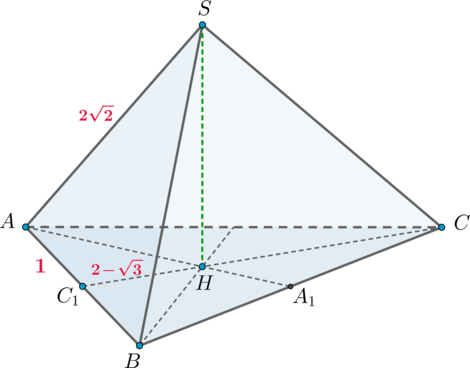
Заметим, что прямоугольный, следовательно, для того, чтобы найти высоту пирамиды,
нужно найти
. Из прямоугольного
:
Следовательно, объем пирамиды равен
Ошибка.
Попробуйте повторить позже
Площадь полной поверхности тетраэдра равна . Найдите площадь полной поверхности
пирамиды, вершинами которой являются точки пересечения медиан граней данного тетраэдра.
Пусть – тетраэдр, точки
— точки пересечения медиан в гранях
соответственно.
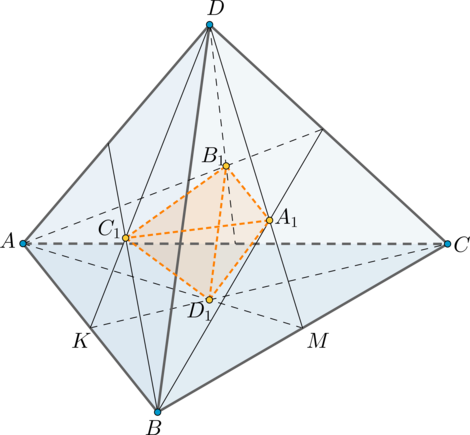
1) Т.к. медианы точкой пересечения делятся в отношении , считая от вершины, то
. Следовательно,
по углу и двум прилежащим
пропорциональным сторонам. Таким образом,
(
как соответственные)
и
.
Аналогичным образом можно доказать, что ,
.
2) с коэффициентом
, то есть
. А вот
с
коэффициентом
(т.к.
– средняя линия), то есть
.
Следовательно, .
Аналогично доказывается, что ,
.
3) Таким образом, все ребра тетраэдра в три раза меньше соответствующих ребер
тетраэдра
, а это значит, что каждая грань тетраэдра
подобна с коэффициентом
соответствующей грани тетраэдра
.
4) Т.к. площади подобных треугольников относятся как квадрат коэффициента подобия, то площадь
каждой грани тетраэдра равна
от площади соответствующей грани тетраэдра
.
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, высота которой равна
, а величина плоского угла при вершине равна
. Вычислите эту площадь, если
,
.
Способ 1.
1) Рассмотрим правильную пирамиду ,
– высота (которая падает в точку
пересечения диагоналей основания),
.
Напомним, что у правильной пирамиды все боковые грани представляют собой равные равнобедренные
треугольники.
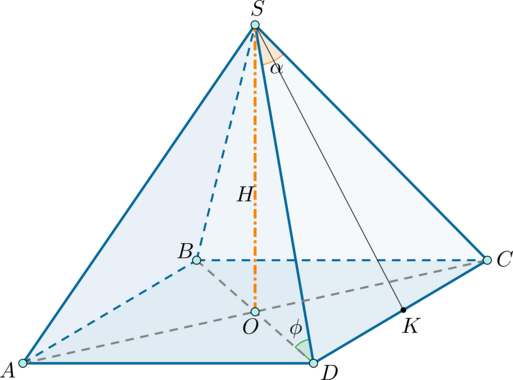
Введем вспомогательный угол между боковым ребром и основанием: .
Тогда , следовательно,
.
Тогда, т.к. площадь треугольника равна полупроизведению сторон на синус угла между ними,
2) Теперь необходимо выразить через данные в условии величины.
Проведем – медиану и высоту в равнобедренном
. Тогда
как диагональ квадрата, следовательно,
. В
:
Разделим равенство на равенство
и получим:
Тогда .
3) Таким образом,
4) Подставляя значения из условия, находим, что
Способ 2.
Пусть длина квадрата основания равна . Тогда
а
Выразим
квадраты длин
и
по теореме Пифагора для треугольника
Запишем теорему косинусов для
, выразив квадрат стороны
Подставим полученное выражение для в формулу
.
Выразим площадь треугольника
Тогда
Ошибка.
Попробуйте повторить позже
В основании треугольной пирамиды лежит равносторонний треугольник
.
Все боковые грани наклонены к плоскости основания под углом
. Пирамида не является
правильной.
а) Докажите, что высота пирамиды падает в центр вневписанной для треугольника
окружности.
б) Найдите объем пирамиды, если , а сторона основания равна
.
а) Пусть – высота пирамиды. Проведем перпендикуляры
к прямым
соответственно. По теореме о трех перпендикулярах наклонные
также будут
перпендикулярны этим прямым. Следовательно, по определению
— линейные
углы двугранных углов между боковыми гранями и основанием. Т.к. эти углы равны, то
по катету и острому углу (
– общий катет).
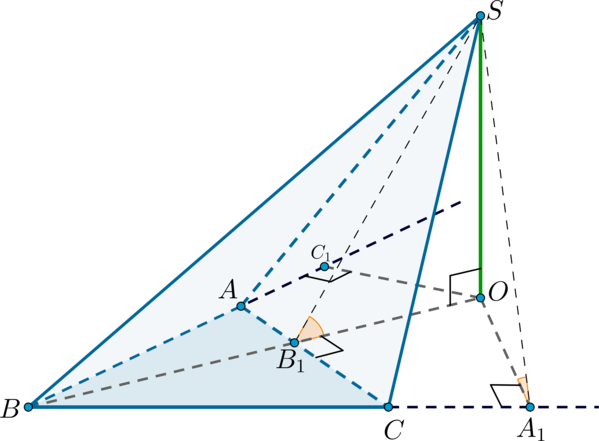
Таким образом, . Таким образом, тока
равноудалена от прямых
. Значит, это либо центр вписанной в
окружности, либо центр вневписанной
окружности (касающейся стороны и продолжений двух других сторон). Т.к. пирамида не является
правильной, то первый вариант не подходит, чтд.
б) Обозначим . Пусть для определенности
– центр окружности, касающейся
стороны
и продолжений сторон
и
. Тогда
лежит на биссектрисе угла
.
Следовательно,
– биссектриса, а т.к.
– правильный, то
. Следовательно, точка
лежит на биссектрисе
.
Значит, . Т.к. отрезки касательных, проведенных из одной точки, равны, то
. Следовательно,
. К тому же
(как половина
).
Значит,
Следовательно, . Из прямоугольного
Таким образом, объем пирамиды равен
б)
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде двугранные углы при ребрах
и
равны. Известно также, что
а) Докажите, что
б) Найдите объем пирамиды, если двугранные углы при ребрах и
равны
а) Рассмотрим пирамиду В ней по условию
Так как и
— равнобедренные, причем
— общее
основание, то высоты к основаниями попадут в одну точку — в середину
стороны
Тогда
Таким образом,
—
линейный угол двугранного угла
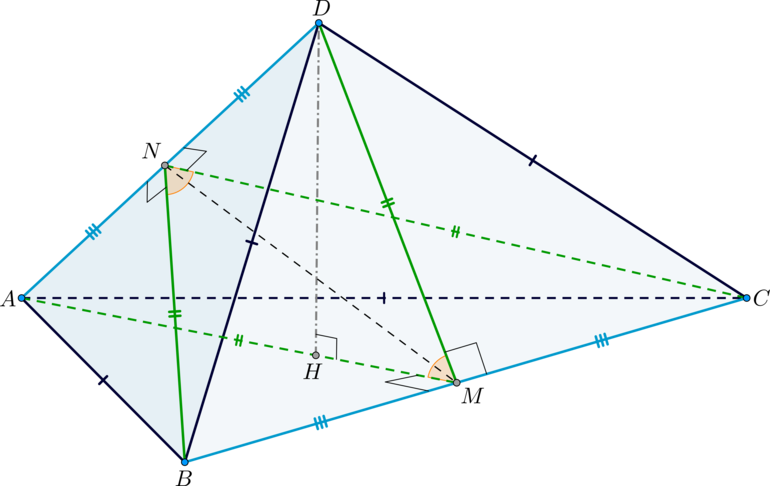
Аналогичным образом строится угол — линейный угол двугранного
угла
где
— середина
Таким образом,
Так как по трем сторонам, то
Аналогично
Значит,
и
— равнобедренные и подобные по двум
пропорциональным сторонам и углу между ними.
Заметим, что плоскости и
имеют две общие точки —
это точки
и
Следовательно, они пересекаются по прямой
Отрезок
— это высота в
и
к основаниям
и
соответственно. Следовательно, эти треугольники равны. Следовательно,
Что и требовалось доказать.
б)

Из пункта а) также следует, что
Так как двугранные углы равны то
и
—
равносторонние.
Пусть
Проведем высоту пирамиды Так как
то по теореме о
трех перпендикулярах
Таким образом, точка
должна
лежать на
причем на середине, так как
— равносторонний.
Тогда
Найдем по теореме Пифагора из
Таким образом,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Параллельно оси цилиндра проведена плоскость, отсекающая от окружности основания дугу, градусная мера которой равна
Диагональ сечения наклонена под углом
к основанию цилиндра.
а) Найдите объем цилиндра, если высота цилиндра равна
б) Вычислите объем цилиндра, если
а) Сечение цилиндра данной плоскостью — это прямоугольник где
Дуга
следовательно,
центральный угол
Объем цилиндра равен
Здесь следовательно, необходимо найти
Рассмотрим прямоугольный треугольник В нем имеем:
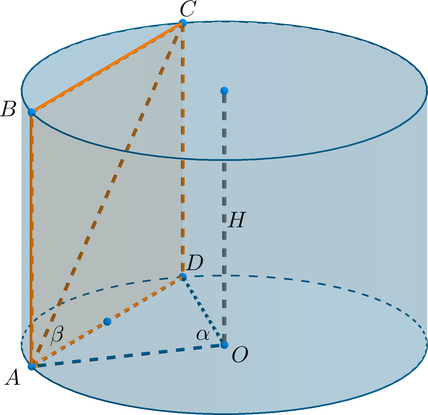
Заметим, что — равнобедренный. Тогда по теореме косинусов
Тогда имеем:
Следовательно, объем цилиндра равен
б) Подставляя значения из условия, получаем:
б) 24
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Образующая усеченного конуса составляет с плоскостью нижнего основания угол . Диагональ его
осевого сечения перпендикулярна образующей конуса. Сумма длин окружностей оснований равна
.
а) Найдите площадь боковой поверхности усеченного конуса.
б) Вычислите эту площадь, если ,
.
а)
1) Достроим усеченный конус до целого конуса. Тогда – высота,
– образующая всего
конуса;
– образующая усеченного конуса,
– осевое сечение усеченного конуса,
–
диагональ этого сечения, которая перпендикулярна
.
– угол между образующей и плоскостью нижнего основания.
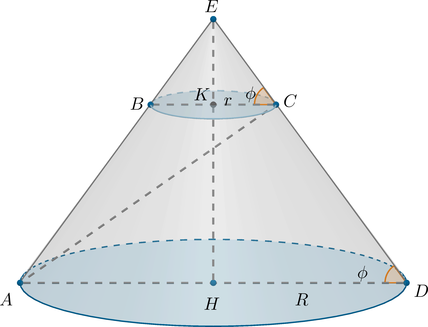
Обозначим за и
– радиусы нижнего и верхнего оснований усеченного конуса соответственно.
Тогда из условия сумма длин окружностей оснований равна
2) Для того, чтобы найти площадь боковой поверхности усеченного конуса, нужно из площади боковой поверхности всего конуса вычесть площадь боковой поверхности маленького конуса:
Заметим, что и
– прямоугольные, следовательно,
Значит, площадь боковой поверхности уже приобретает вид:
Необходимо найти .
3) Т.к. , то
– прямоугольный, следовательно,
Из данных второго пункта мы можем сказать, что
Таким образом, имеем:
Но , следовательно,
, следовательно,
Подставляя это значение для в
, находим, что
Таким образом,
4) Значит, площадь боковой поверхности равна
б) Подставляя значения из условия и помня, что , найдем площадь боковой
поверхности:
а)
б)
Ошибка.
Попробуйте повторить позже
На ребре правильной четырехугольной пирамиды
с основанием
отмечена точка
причем
Точки
и
—
середины ребер
и
соответственно.
а) Докажите, что сечение пирамиды плоскостью является
равнобедренной трапецией.
б) Найдите отношение объемов многогранников, на которые плоскость
разбивает пирамиду.
а) Пусть — высота пирамиды, следовательно, так как пирамида правильная,
— точка пересечения диагоналей квадрата
Тогда отрезок
пройдет через точку
причем
Построим сечение пирамиды
плоскостью
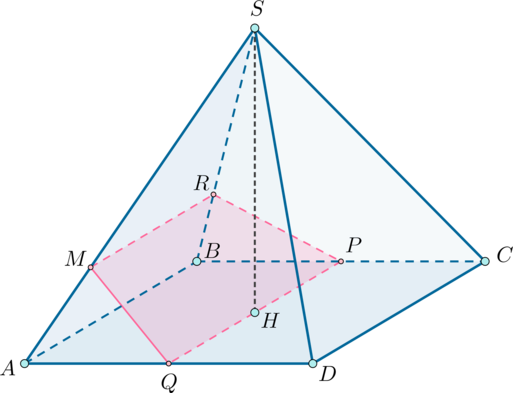
Плоскости и
пересекаются по прямой
плоскости
и
— по прямой
Так как
то плоскости
и
пересекутся по прямой
Действительно, если это не так, то есть то
— это общая
точка плоскости
и плоскости
следовательно,
Но
следовательно,
что невозможно, так как
Таким образом, — трапеция.
Так как то по теореме Фалеса
Так как пирамида правильная, то ее боковые ребра равны, следовательно,
Также
и все боковые грани представляют собой
равные равнобедренные треугольники, то есть, например,
Следовательно,
откуда
Значит, — равнобедренная трапеция.
б) Нужно найти отношение Пусть
То есть нужно найти
Введем обозначения:
Тогда
Найдем Тогда
В пирамиде
— вершина,
— основание. Для того, чтобы
найти ее объем, нужно найти высоту
Пусть — середина
Так как
— середина
и трапеция
равнобедренная, то
то есть
— высота трапеции.
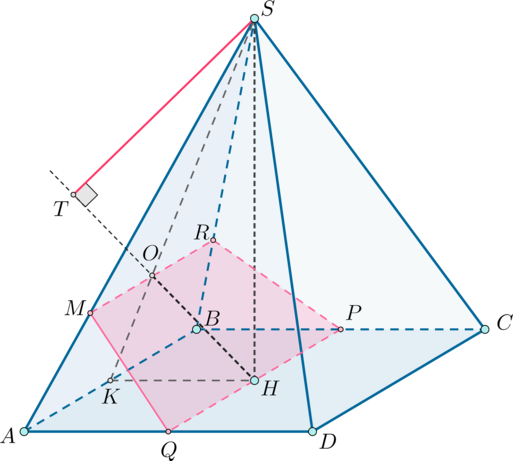
Утверждение: точка лежит на прямой
Действительно, пусть проведена Тогда, так как
(наклонная), то по теореме о трех перпендикулярах
(проекция). Так
как к одной прямой в плоскости не может быть проведено два различных
перпендикуляра
и
следовательно,
Прямая пересечет
в точке
— середине
так как
—
середина
и
Тогда
с коэффициентом
следовательно,
Рассмотрим плоскость и трапецию
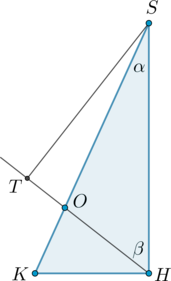
Из
Так как
то
следовательно,
Тогда по теореме косинусов из
Заметим, что
По теореме синусов из
Тогда из прямоугольного
Таким образом,
Тогда
Также
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырехугольной пирамиды лежит равнобедренная трапеция
, причем
,
. Угол между прямыми
и
равен
. Известно, что
–
высота пирамиды.
Внутри пирамиды расположен конус так, что основание конуса – вписанная в треугольник
окружность, а вершина конуса принадлежит ребру
. Найдите объем конуса.
Если – точка пересечения прямых
и
, то
. Так как также
(так как трапеция равнобедренная), то
равносторонний и
. Следовательно, и
.
Пусть – центр основания конуса,
– вершина. Тогда
.
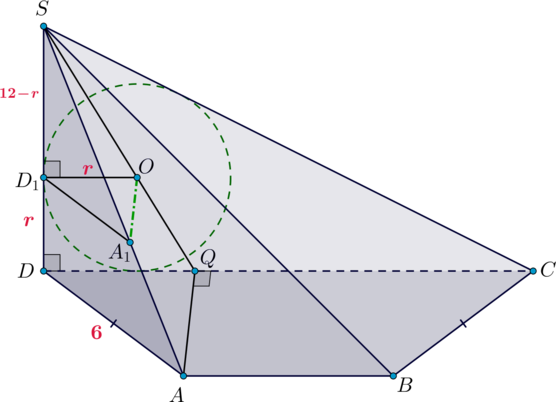
Заметим, что если в плоскости провести
, то
(так как
и
). Следовательно, прямые
и
параллельны, следовательно, лежат в одной
плоскости, причем это плоскость
(так как
).
Рассмотрим грань . Пусть
– радиус вписанной окружности. Тогда
по
свойству прямоугольного треугольника.
, следовательно,
Следовательно,
Тогда объем конуса равен:



