Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Функция определена при всех . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная отрицательна, то есть функция
убывает; при
производная положительна, то есть
функция возрастает. Следовательно,
является точкой минимума.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Функция определена при всех . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная отрицательна, то есть функция
убывает; при
производная положительна, то есть
функция возрастает. Следовательно,
является точкой минимума.
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции
Функция определена при всех . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная положительна, то есть функция
возрастает; при
производная отрицательна, то
есть функция убывает. Следовательно,
является точкой максимума.
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции
Функция определена при всех Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого
найдем ее производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная положительна, то есть функция
возрастает. При
производная
отрицательна, то есть функция убывает. Следовательно,
является точкой максимума.
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на отрезке
Найдём производную функции :
Приравняем производную к нулю и найдём критические точки:
Точка не лежит на отрезке, её мы из рассмотрения исключаем.
Рассмотрим значения функции в точке экстремума и на границах
отрезка
Наименьшее значение функции на отрезке равно 14.
Ошибка.
Попробуйте повторить позже
Найдите точку локального максимума функции
.
ОДЗ: . Решим на ОДЗ:
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
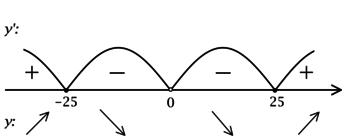
3) Эскиз графика :
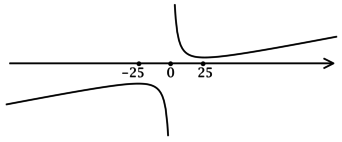
Таким образом, – точка локального максимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции на промежутке
.
ОДЗ: .
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Найдём промежутки знакопостоянства на рассматриваемом промежутке
:

4) Эскиз графика на промежутке :
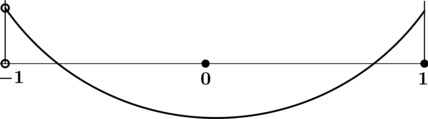
Таким образом, – точка минимума функции
на промежутке
.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции на отрезке
Найдем ОДЗ: — любое число.
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:
Производная существует при любом
2) Найдём промежутки знакопостоянства и промежутки монотонности

3) Найдём промежутки знакопостоянства и промежутки монотонности
на отрезке

4) Эскиз графика на отрезке
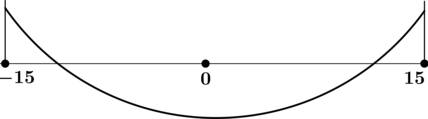
Таким образом, — точка минимума функции
на отрезке
Ошибка.
Попробуйте повторить позже
Найдите точку локального минимума функции
Найдем ОДЗ: .
1) Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует):
2) Найдём промежутки знакопостоянства и промежутки монотонности
:
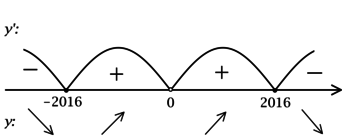
3) Эскиз графика :
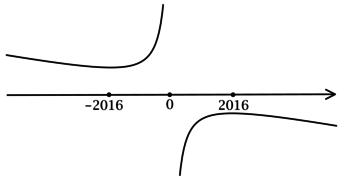
Таким образом, — точка локального минимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции .
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика:
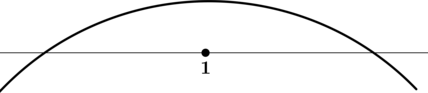
Таким образом, – точка максимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку локального минимума функции
.
ОДЗ: . Решим на ОДЗ:
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
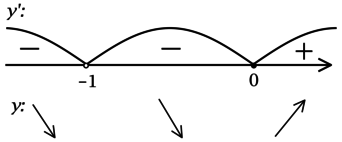
3) Эскиз графика :
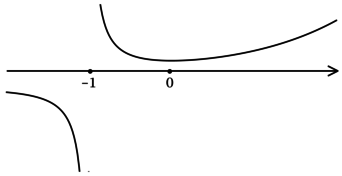
Таким образом, – точка локального минимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции на промежутке
.
ОДЗ: .
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Найдём промежутки знакопостоянства на рассматриваемом промежутке
:

4) Эскиз графика на промежутке :
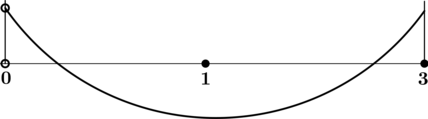
Таким образом, – точка минимума функции
на промежутке
.



