МВ / Финашка (Миссия выполнима. Твоё признание — финансист) —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
МВ / Финашка (Миссия выполнима. Твоё признание — финансист)

Тема МВ / Финашка (Миссия выполнима. Твоё признание — финансист)

МВ / Финашка (Миссия выполнима. Твоё признание — финансист)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы МВ / Финашка (Миссия выполнима. Твоё признание — финансист)

Отбор МВ (Финашки)

Алгебраические текстовые задачи на МВ (Финашке)

Последовательности и прогрессии на МВ (Финашке)

Тригонометрия на МВ (Финашке)

Тождественные преобразования на МВ (Финашке)

Системы на МВ (Финашке)

Планиметрия на МВ (Финашке)

Стереометрия на МВ (Финашке)

Теория чисел на МВ (Финашке)

Комбинаторика на МВ (Финашке): графы, турниры, множества, способы

Функции на МВ (Финашке)

Параметры на МВ (Финашке)

Подтемы раздела мв / финашка (миссия выполнима. твоё признание — финансист)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#81381

Про натуральные числа $X,Y$ и $Z$ известно, что они различны и не превосходят 100. Мы можем выписать любую последовательность ${a1,...,a100}$ , содержащую все натуральные числа от 1 до 100. Какое наименьшее число последовательностей нужно выписать, чтобы среди них наверняка имелась такая, в которой два или три подряд идущих члена принадлежат множеству ${X;Y ;Z}?$

Источники: Миссия выполнима - 2024, 11.8 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Для начала нужно понять, как вообще подступаться к такой задаче. Через что её решать? У нас есть числа, и мы рассматриваем, стоят ли они подряд в последовательностях. Какая вещь помогает рассмотреть отношения между какими-то объектами?

Подсказка 2

Это графы! Пусть у нас есть какое-то количество последовательностей. Вершины графа - это числа от 1 до 100, а рёбра между вершинами x и у проводятся, если в одной из последовательностей числа х и у были подряд идущими членами. Теперь надо понять, при каком наименьшем числе последовательностей обязательно не найдется тройки, внутри которой нет рёбер.

Подсказка 3

Если сложно угадать число, попробуйте рассмотреть ситуацию, когда у нас n последовательностей. Как тогда можно оценить степени вершин?

Подсказка 4

В каждой последовательности число соседствует не более чем с двумя другими числами, то есть степень каждой вершины не превосходит 2n. Подумайте, при каком наименьшем n в любой тройке вершин будет хотя бы одно ребро. Это и будет ответом на задачу. И не забудьте про пример!

Показать ответ и решение

Сначала покажем, что $24$ последовательностей не хватит.

Построим граф, вершины которого это числа от $1$ до $100$ , а рёбра между вершинами $a$ и $b$ проводятся, если в одной из последовательностей числа $a$ и $b$ были подряд идущими членами.

Так как суммарно во всех $24$ -x последовательностях каждое число будет соседом не более $2 ⋅24 =48$ других чисел, степень каждой вершины в этом графе не превосходит $48$ .

Тогда выберем в графе две несмежные вершины $x,y.$ Так как степень каждой из них не более $48$ , а всего вершин $100$ , то найдется хотя бы $1$ вершина $z$ , которая не соседствует с обеими вершинами $x,y$ . Тогда множество чисел ${x,y,z}$ не будет удовлетворять условию задачи (ни в одна последовательности нет двух или трех подряд идущих членов, которые содержатся в ${x,y,z}$ )

_________________________________________________________________________________________________________________________________________________________________________________

Пример на $25$ последовательностей опишем пример в терминах графа.

Разделим $100$ чисел на две равные группы: например, $1,2,3,...,50$ и $51,52,...,100$ .

Отдельно расставим первые $50$ чисел в $25$ последовательностей длиной $50$ , чтобы любые $2$ числа были соседями в хотя бы одной из $25$ последовательностей. (То есть на языке графов: нужно покрыть $25$ путями полный граф на $50$ вершинах). И аналогично поступим со второй группой $50$ чисел, а потом просто “склеим” последовательности. Например, если первая последовательность в первой группе это $1,2,...,50$ , а первая последовательность во второй - это $51,52,...,100$ , то склеиваем и получаем $1,2,...,50,51,52,...,100$ .

Опишем построение $25$ последовательностей длиной $50$ . Поместим вершины в правильный многоугольник и покроем полный граф на этом подмножестве вершин $25$ последовательностями (то есть путями проходящими по всем вершинам), идущими зигзагом через многоугольник с поворотом каждого пути на кратный $-π-- n− 1$ угол. На картинке пример построения $4$ последовательностей, для $8$ чисел:

$PIC$

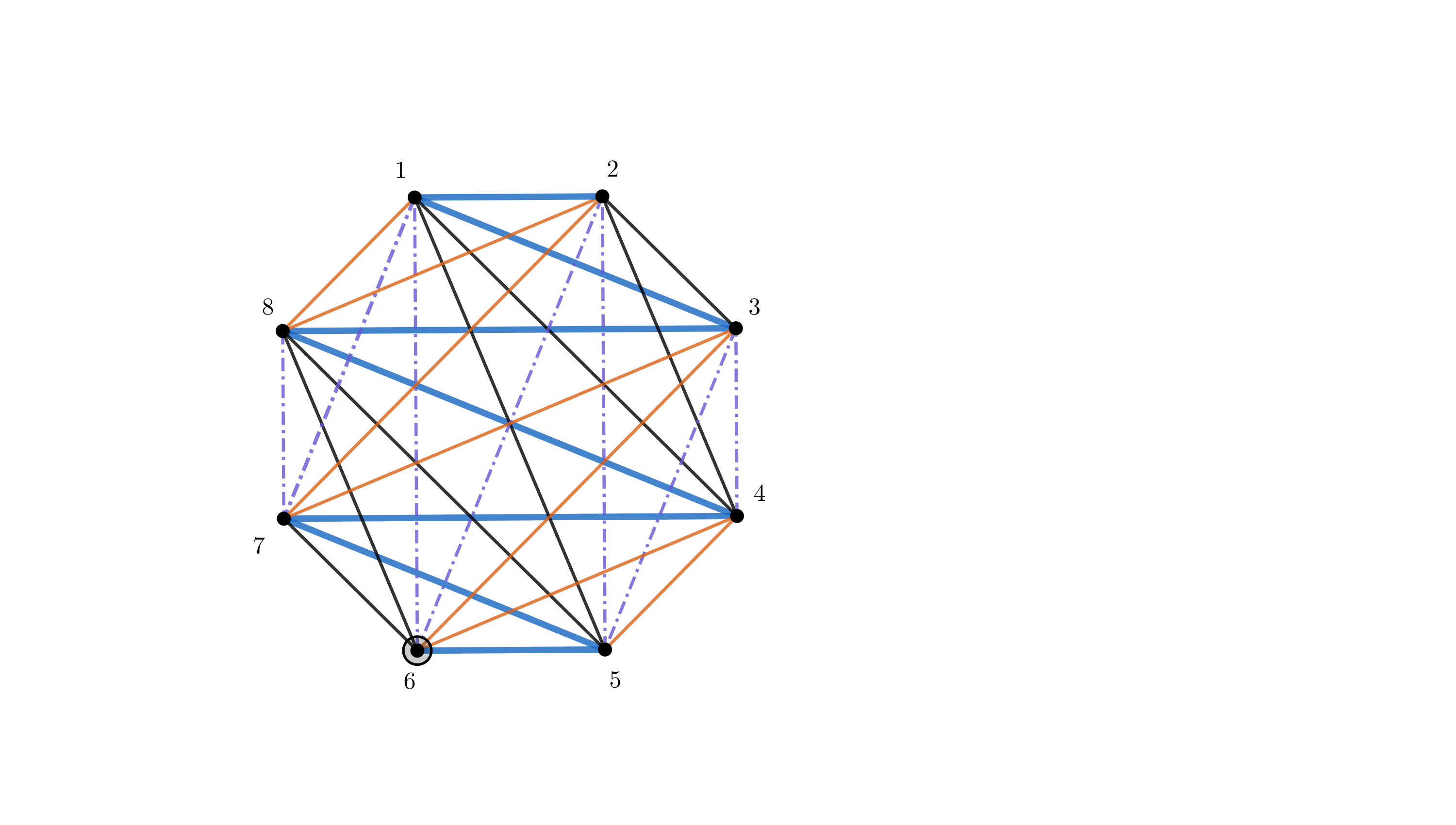
Теперь поясним, почему после "склейки"полученные $25$ последовательностей будут удовлетворять условию. Какие бы числа $X,Y,Z$ , мы ни взяли, либо два из них будут среди чисел от $1$ до $50$ , либо среди чисел от $50$ до $100$ . Тогда два числа из одно группы соединены ребром, то есть являются соседями в одной из $25$ последовательностей. Этого мы и добивались.

Ответ: 25

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#81380

При каких значениях параметра $b$ существует прямая, касающаяся графика функции $f(x)=x4+ bx2+x$ в двух точках? Для каждого такого значения параметра $b$ найдите уравнение соответствующей прямой.

Источники: Миссия выполнима - 2024, 11.7 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Что означает касание? Какую систему нам нужно решать? Сколько корней у неё должно быть?

Показать ответ и решение

Условие, что прямая вида $y =kx+ m$ касается графика $y = f(x)$ означает равенство функций и равенство производных в точке касания:

({ 4 2 x + bx +x =kx+ m (4x3+ 2bx+ 1= k

Нас интересует, когда эта система имеет ровно $2$ корня. Заметим, что система эквивалентна

( { x4 +bx2 = (k − 1)x+ m ( 4x3+ 2bx= k− 1

То есть должна существовать прямая $y =(k− 1)x +m$ , которая касается графика $y = x4+ bx2$ .

При $b≥ 0$ ее производная $4x3+ 2bx$ монотонная функция, а значит, $4x3+ 2bx= k− 1$ имеет не более одного решения, тогда и вся система имеет не более одного решения.

При $b< 0$ можно заметить, что касательные в точках локального минимума $∘--- x1,2 =± −-b 2$ (нашли их как корни производной $3 4x + 2bx =0$ ) имеют одинаковый коэффициент наклона $0$ , а также в этих точках значение функции совпадает в силу чётности. Тогда прямая $b2 b2 b2 y =x41+ bx21 = 4-− 2-= −4$ будет касательной сразу к двум точкам (только к двум точкам, потому что в точке $x= 0$ касательная $y = 0$ ; в других же точках коэффициент наклона касательной не $0$ ).

Возвращаясь к изначальным обозначениям, получаем $2 k − 1 =0;m =− b 4$ . То есть искомая касательная это $2 y = x− b 4$ .

Ответ:

при $b <0$ , прямая $y =x− b2 4$

Ошибка.
Попробуйте повторить позже

Задача 3#81379

Два треугольника пересекаются по шестиугольнику $ABCDEF$ , в котором

∘ ∘ ∘ ∘ ∠A = ∠B =∠C = 100 ,∠D =130 ,∠E = 140,∠F =150

Найдите углы этих треугольников.

Источники: Миссия выполнима - 2024, 11.6 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Обратите внимание, что есть два случая для пересечения треугольников.

Показать ответ и решение

Случай $1$ (стороны треугольника - тройки несмежных сторон):

$PIC$

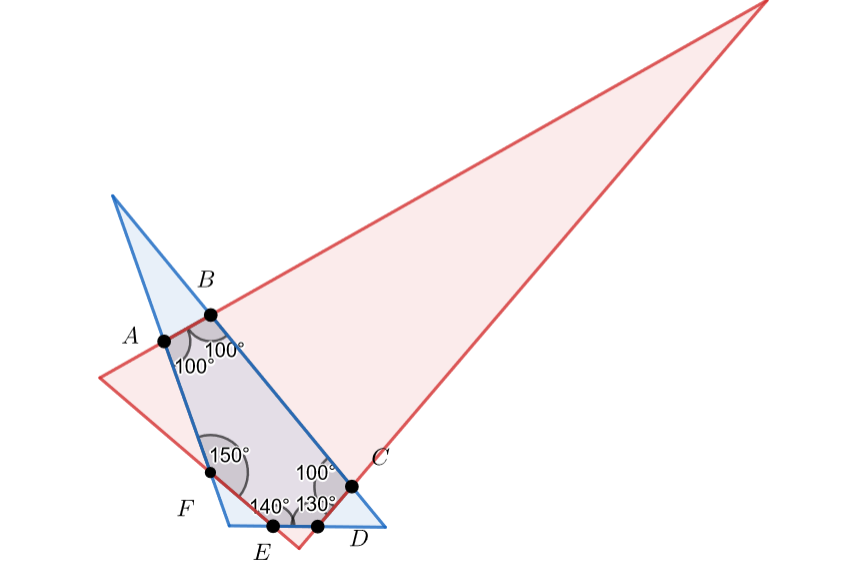
В таком случае все углы треугольников легко находятся, как $∘ ∘ ∘ ∘ 180 − (180 − α)− (180 − β)=α +β − 180$ , где $α,β$ - два соседних угла шестиугольника.

Тогда получаем, что углы красного треугольника равны $∘ ∘ ∘ 20 ,70 ,90$ , а углы синего - $∘ ∘ ∘ 20,50,110$ .

Случай $2$ (один из углов шестиугольника совпадает с углом треугольника):

$PIC$

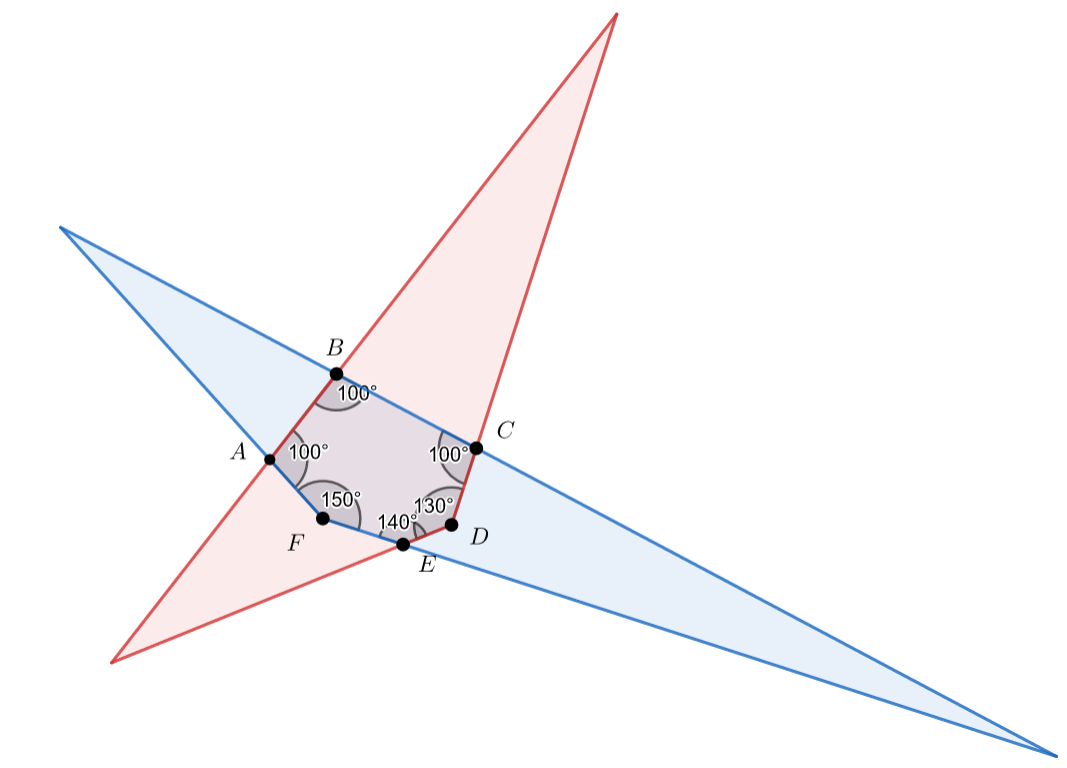
Заметим, что это единственное возможное положение в этом случае. Углы синего треугольника равны $150∘$ ; $180∘− (180∘− ∠A )− (180∘ − ∠B )=20∘$ и $10∘$ .

Углы красного треугольника будут равны $130∘;$ $180∘ − (180∘− ∠B)− (180∘− ∠C)= 20∘$ и $30∘$ .

Ответ:

$20∘,50∘,110∘$ и $20∘,70∘,90∘$ ; или $10∘,20∘,150∘$ и $20∘,30∘,130∘$

Ошибка.
Попробуйте повторить позже

Задача 4#81378

Решите уравнение

2x−-1 x-+3- arctg x+ 2 + arctg3x− 1 = x

Источники: Миссия выполнима - 2024, 11.5 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Арктангенс — обратная функция от тангенса, поэтому, ровно как мы нередко логарифмируем в уравнениях, мы можем взять тангенс от обеих частей и получить следствие (заметьте, что это будет неравносильный переход).

Подсказка 2

Если взять тангенс от обеих частей, то можно раскрыть тангенс от суммы арктангенсов. При этом это будет равно tg(x). Тогда слева у нас получится 7, а справа tg(x). Тогда понятно какие значения может принимать х. Остается понять, подходят ли эти значения или нет. Как можно понять, подходят ли? Мы можем посмотреть на то, почему переход взятия тангенса неравносилен и на какие случаи он разбивается.

Подсказка 3

Он неравносилен, так как если tgx = tgy, то либо x = y, либо x = y + pi, то есть, так как у нас все происходит на интервале от -pi до pi, то по сути, нам надо проверить, что при подстановке наших корней, знак левой и правой части будет одинаковый. Это уже чисто техническая задача, при решении которой нужно просто грубо оценивать arctg7.

Показать ответ и решение

Посчитаем

2x-− 1 -x+-3 tg(arctg x+ 2 +arctg3x − 1)=

2x−-1 x+3- = -x+22x−+1-3x−x1+3-= 1− x+2-⋅3x−1-

7x2+ 7 = -x2+1-= 7

Тогда для корня уравнения $tg(x)= 7$ . При этом так как $π π − 2 < arctg(t)< 2$ , получаем $− π < x< π$ .

Откуда получаем, что кандидатами в корни могут быть только $arctg 7$ и $arctg 7− π$ . Покажем, что они подходят: для этого достаточно проверить, что при подстановке этих значений левая часть примет тот же знак, что и правая. (Так как левая часть всегда равна $arctg 7$ или $arctg7− π$ )

Для $x= arctg7$ имеем

arctg 2x-− 1 =arctg(2−-5-)>0, x+ 2 x+ 2

так как $2> 5> --5- 3 x +2$ для $x= arctg7$ в силу того, что $arctg7> arctg√3 = π> 1 3$ .

А также

x-+3- 1 -10-- arctg3x− 1 = arctg(3 + 9x − 3)> 0

Для $x= arctg7− π$ имеем

2x − 1 5 arctg-x+-2 =arctg(2− x+-2)<0,

так как

2< --5- ⇐⇒ 1> x+ 2> 2π − π+ 2= 2− 3π >0 x+ 2 5 5

А также

arctg x-+3-= arctg(1 +-10-)< 0, 3x− 1 3 9x − 3

потому что

1-< --1-- ⇐⇒ x< 0,3 − 9x< 30 (x> π − π > −3) 30 3− 9x 3

Значит, оба этих значения — корни.

Ответ:

$arctg7$ и $arctg7 − π$

Ошибка.
Попробуйте повторить позже

Задача 5#81377

Длина ребра куба $ABCDA ′B′C′D′$ равна 1. Найдите радиус сферы, проходящей через точку $B$ и касающейся прямых $AD,AA′$ и $′ ′ A B$ .

Источники: Миссия выполнима - 2024, 11.4 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Тут у нас и параллельные прямые, и биссектрисса - давайте поищем равные углы. Помним, что биссектрисса отсекает от параллелограмма равнобедренный треугольник.

Подсказка 2

Верно, получаем MCK равнобедренный. Тогда ОС (где О - центр окружности) - серединный перпендикуляр КМ, а треугольники KOC и МОС равны и равнобедренны. На этом этапе давайте остановимся в изучении чертежа и подумаем, как нам доказать требуемое. Какой признак может указывать на принадлежность точки О описанной окружности BCD?

Подсказка 3

Конечно, в нашем случае проще всего будет доказывать через равенство вписанных углов. Для каких двух углов будет удобнее это доказать?

Подсказка 4

Конечно, легче находится, что OBC и ODC равны и опираются на дугу ОС. Это несложно вывести, если увидеть равенство треугольников BKO и DCO. Теперь остаётся только последовательно всё доказать

Показать ответ и решение

Введём декартову систему координат с центром в точке $A$ , ось абсцисс — луч $AD$ , ось ординат — луч $AA ′$ , ось аппликат — луч $AB$ .

Пусть $′ O$ — проекция центра сферы на грань $′ ′ AA B B$ куба. Определим ее местоположение. Так как сфера касается прямых $′ ′′ AA ,A B$ и проходит через точку $B$ , то расстояние от точки $′ O$ до прямых $′ AA$ и $′ ′ A B$ и точки $B$ одинаково (обозначим его $r$ ). Тогда $′ O$ лежит на луче $′ A B$ , который является биссектрисой угла $′ ′ AA B$ . Осталось учесть условие, что центр сферы касается прямой $AD$ , то есть нужно проверить, что расстояние от центра до прямой $AD$ совпадает с радиусом сферы $OB$ .

Заметим, что есть два случая расположения точки $′ O$ (на рисунке показаны разными цветами):

$PIC$

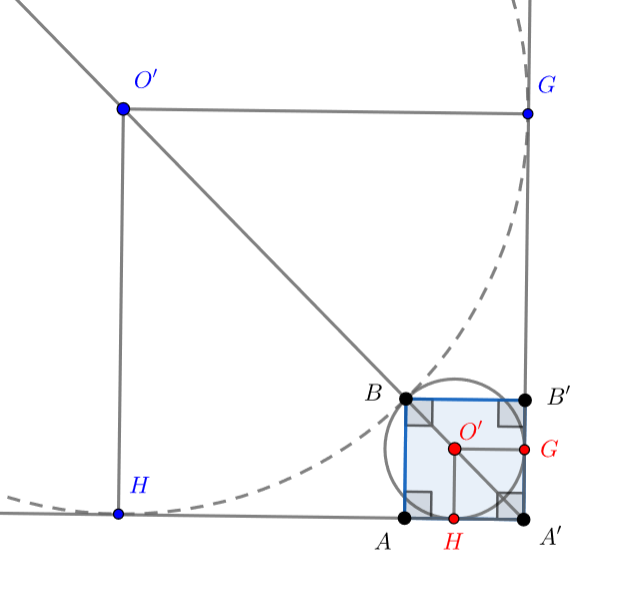
Случай 1: точка $O ′$ лежит на диагонали $A ′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-− r)2$ , откуда $r =2− √2$ . Значит, центр сферы $O$ имеет координаты $(x1;√2-− 1;2− √2)$ .

Расстояние до прямой $AD$ равно $∘(√2−-1)2-+(2−-√2)2$ . То есть радиус $OB = ∘(√2-− 1)2+(2−-√2)2 = ∘9−-6√2.$

Случай 2: точка $O ′$ лежит на продолжении луча $A′B$ .

Тогда из теоремы Пифагора для прямоугольного треугольника $O ′HA ′$ получим: $r2+ r2 = (√2-+r)2$ , откуда $r =2+ √2$ . Значит, центр сферы $O$ в этом случае имеет координаты $(x ;−√2-− 1;2+ √2) 2$ .

Расстояние до прямой $AD$ равно $∘--√-----2-----√--2 (− 2− 1) + (2+ 2)$ . То есть радиус $∘ --√----2-----√--2- ∘ ---√-- OB = (− 2− 1)+ (2+ 2) = 9+6 2.$

Ответ:

$∘9-±-6√2$

Ошибка.
Попробуйте повторить позже

Задача 6#81373

Для каждого натурального числа $n$ положим

-(−3)n-- p(n)= 3n+ 317

Вычислите сумму

p(1)+ p(2)+ ...+p(33)

Источники: Миссия выполнима - 2024, 11.3 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Когда у нас есть такая вот телескопическая сумма, то что мы обычно любим делать? Либо преобразовывать каждый элемент, либо брать их по группам и говорить, что в каждой группе сумма хорошая. Но обычно группы из двух чисел. Какие тогда два числа мы обычно берем из таких сумм?

Подсказка 2

Сумма первого и последнего равна (-1)^n. А может быть, так работает и для суммы k-ого с начала и k-ого с конца? Проверьте это и запишите ответ.

Показать ответ и решение

Заметим, что для $1≤ n≤ 17$

-(−3)n-- -(−-3)34−n-- -(−1)n-- (−1)n317−n n p(n)+p(34 − n)= 3n+ 317 + 334−n+ 317 = 1+ 317−n + 1+ 317−n =(−1)

Тогда

(−1)17 − 1 p(1)+ p(2)+ ...+ p(33)= (− 1)1+ (− 1)2+ ...(−1)16+ --2-- =-2-

Ответ:

$− 1 2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#81371

Каким наибольшим может быть значение выражения $A +B$ , если $A$ и $B$ – числа, удовлетворяющие следующей системе неравенств

( 3A +5B ≤11 |{ |( 4A +3B ≤10 7A +4B ≤18

Источники: Миссия выполнима - 2024, 11.2 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала поймём, что нам неудобно работать с величинами A и B. Так как нам нужно максимизировать не их, а их сумму (это не всегда одно и то же, если мы максимизируем каждое по отдельности, у нас может получиться оценка, которая не достигается), то давайте обозначим за S = A + B сумму этих чисел и заменим везде в неравенствах, чтобы в них фигурировало только S и A (система с тремя переменная - это совсем грустно). Тогда чтобы решить задачу, нам остаётся дать оценку на A снизу через S, так как тогда два вторых получившихся неравенства дадут нам выбор из минимумов

Подсказка 2

Подставляя оценку A >= (5S - 11) / 2. в два оставшихся неравенства, у нас получается оценка на S сверху. Значит, остаётся выбрать то, что даёт минимальную. И всё?

Подсказка 3

Конечно, нет. Нам нужно привести пример. Однако здесь, чтобы привести пример, достаточно просто «развернуть» наши действия, посмотреть в какой точке достигается равенство и так найти, чему должно быть равно А.

Показать ответ и решение

Обозначим за $S =A +B$ , тогда систему можно переписать в виде:

( 5S − 2A ≤11 |{ |( 3S +A ≤10 4S +3A ≤18

Представим первое неравенство, как $A ≥ 5S−11, 2$ тогда получаем

(| 5S−-11 |||{ 2 ≤ A | 11S−2-11≤ 3S+ A≤ 10 |||( 23S−-33≤ 4S+ 3A ≤ 18 2

Откуда получаем оценку

2⋅10+-11-18⋅2+33- 31 S ≤ min( 11 , 23 )= 11

При этом равенство достигается в точке области

17 14 A= 11,B =11

(являющейся точкой пересечения прямых $3A +5B = 11,4A+ 3B =10$ ).

Ответ:

$31 11$

Ошибка.
Попробуйте повторить позже

Задача 8#81368

Среди людей, не говорящих по-английски, $4%$ говорят по-французски, а среди людей, не говорящих по-французски, $20%$ говорят по-английски. Во сколько раз число людей, не говорящих по-французски, больше числа людей, не говорящих по-английски?

Источники: Миссия выполнима - 2024, 11.1 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

Пусть на английском НЕ говорят х человек, а на французском - y. Какое значение мы можем однозначно выразить, используя эти переменные?

Подсказка 2

Да, можем из условия найти количество людей, не знающих ни один из этих языков, и составить уравнение для x y. Теперь нужно только аккуратно всё посчитать и найти отношение

Показать ответ и решение

Пусть $x$ — число людей, не говорящих по-английски, а $y$ — число людей, не говорящих по-французски. Тогда из условия людей, не говорящих ни на одном из языков: $96%$ от $x$ , а с другой стороны $80%$ от $y$ .

Откуда $0.96x = 0.8y$ , то есть $y x = 1.2$ .

Ответ: 1,2

Ошибка.
Попробуйте повторить позже

Задача 9#76730

Десятичная запись суммы $1+ 11+ 111+ ...+ 11...1$ оканчивается на 2023. Каким наименьшим может быть количество цифр в последнем слагаемом?

Источники: Миссия выполнима - 2023, 11.3 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Давайте посмотрим на эту сумму по модулю 10000: она должна быть равной 2023. С другой стороны, чему она равна, если у нас, например, n слагаемых в ней?

Подсказка 2

Она равна 1+11+111+1111(n-3), где n какое-то натуральное число. Как из этого выразить n через m?

Подсказка 3

Осталось понять, при каком минимальном m у нас найдётся такое n, выделив целую часть или посмотрев по модулю 1111)

Показать ответ и решение

Указанную сумму обозначим через $S$ , а количество слагаемых в ней (совпадающее с количеством цифр в последнем слагаемом) - через $n$ . Тогда сумма остатков слагаемых от деления на 10000 равна $123 +1111(n− 3)$ , и дает при делении на 10000 такой же остаток, что и $S$ .

Поэтому выполнено равенство $123+ 1111(n− 3)= 10000m+ 2023$ , где $m$ - некоторое натуральное число. Отсюда

10000m + 2023− 123 m + 789 n− 3= ------1111------= 9m + -1111- +1

Наименьшее $m$ , при котором $m+ 789$ делится на 1111, равно 1111-789=322.

Следовательно, искомое решение $n$ равно $3+ 9322 +1+ 1= 2903$ .

Ответ: 2903

Ошибка.
Попробуйте повторить позже

Задача 10#63952

На плоскости отмечено 9 различных точек, среди которых есть красные, синие и зеленые. Точек других цветов нет. Известно, что сумма всех попарных расстояний между красными и синими точками равна 13, между красными и зелеными равна 11, а между синими и зелеными равна 1. Каким может быть количество красных отмеченных точек?

Источники: Миссия выполнима - 2023, 11.8 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Пупупу…давайте подумаем, а что можно сказать про тройку из трех точек различных цветов?

Подсказка 2

Верно, для каждой такой тройки выполняется неравенство треугольника!(убедитесь, что если точки лежат на одной прямой, то это неравенство тоже выполняется) Так, но это условие мы получили только для одной конкретной тройки точек, а можно ли получить что-то про все точки сразу?

Подсказка 3

Да, можно сказать, что сумма всех расстояний между красными и синими точками не больше чем сумма суммы расстояний между красными и зелеными точками и суммы расстояний между синими и зелеными! А как это записать математически?

Подсказка 4

Конечно, иными словами: 13r ≤ 11q + p, где r- количество красных точек, q – синих точек, p – зеленых точек! Аналогично можно сказать, что 11q ≤ 13r+p(опять же в силу неравенства треугольника) А также не забываем про условие, что p+q+r=9. Осталось найти возможные значения p, q, r и привести пример, что каждый случай достигается!

Показать ответ и решение

Пусть отмечены красные точки $A ,...A 1 p$ , синие точки $B ,...B 1 q$ , и зеленые точки $C ,...C 1 r$ .

Поскольку для каждой точки $(AiBjCk)$ выполняется неравенство треугольника $AiBj ≤ AiCk+ BjCk$ , то

∑p q∑ ∑r ∑p q∑ ∑r AiBj ≤ (AiCk +BjCk) i=1j=1k=1 i=1j=1k=1

Откуда $13r≤ 11q+p$ .

Аналогично, просуммировав неравенства $A C ≤ AB +B C i k i j j k$ , получим $11q ≤ 13r +p$ .

Далее перебором можно установить, что найденным соотношениям и равенству $p+q +r= 9$ удовлетворяют ровно две тройки натуральных чисел

p= 5,q = 2,r= 2 и p= 7,q =1,r= 1.

Покажем, что оба найденных варианта могут быть реализованы на прямой. Каждую из отмеченных точек будем задавать ее координатой.

Первый вариант: $A = 3-,A = 1,A = 3,A =2,A = 17B = 0,B = 1,C = 1,C = 3 1 16 2 3 2 4 5 16 1 2 8 1 4 2 8$

Второй вариант: $A = 1,A = 1,A = 1,A = 2,A = 5,A = 5,A =7 B = 0,C = 1 1 6 2 3 3 2 4 3 5 6 6 7 1 1$ .

Ответ:

5 или 7

Ошибка.
Попробуйте повторить позже

Задача 11#63951

Найдите наименьшее значение функции

∘ --2------- ∘--2------- f(x)= 2x + 2x +13+ 2x + 8x+ 26.

Источники: Миссия выполнима - 2023, 11.7 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Конечно, эту задачу можно решить с помощью производной… Но давайте попробуем найти более красивое решение! Давайте подумаем, нам нужно найти минимальное значение суммы двух корней, а что мы знаем про корни и как тогда можно представить их?

Подсказка 2

Да, корни всегда положительны! Поэтому мы можем представить их как отрезок или же вектор на плоскости! То есть, корень – это длина нашего вектора! В таком случае, каких векторы можно взять(с какими координатами), чтобы длина первого равнялась первому корню, а длина второго равнялась второму корню?

Подсказка 3

Так, длина вектора – это корень из суммы квадратов его координат! Первое подкоренное выражение обращается в ноль при x=-3 и при x=2, а второе при x=1 и при x=-5. Поэтому первый вектор равен (x+3;2-x), а второй вектор: (1-x)(x+5). Что можно сказать про сумму этих векторов?

Подсказа 4

Да, сумма этих векторов равна другому вектору: (4; 7). А длина этого вектора равна √65. Но заметим, что сумма длин исходных векторов не меньше чем длина получившегося вектора! Осталось показать, что минимальное значение достигается и задача решена!

Показать ответ и решение

Рассмотрим векторы

⃗ ⃗ ⃗a= (x +3;2− x),b= (1− x;x+ 5) и⃗s= ⃗a+ b= (4;7)

Так как

∘ -2-------- ⃗ ∘ --2------- |⃗a|= 2x + 2x+ 13, |b|= 2x + 8x +26

то

f(x)= |⃗a|+|⃗b|≥|⃗a+⃗b|= |⃗s|= √65

Равенство $|⃗a|+|⃗b|= |⃗a +⃗b|$ выполняется, когда эти векторы сонаправлены; соответствующие значения $x$ является корнем уравнения $x1+−3x = 2−xx+5$ и равно $− 1311-$ .

Ответ:

$√65$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#63950

B неравнобедренном треугольнике $ABC$ проведены биссектрисы $AA 1$ и $BB 1$ . Известно, что $AA :BB =AC :BC 1 1$ и что радиус окружности, касающейся стороны $AB$ и продолжений сторон $CA$ и $CB$ , равен 1. Найдите периметр треугольника $ABC.$

Источники: Миссия выполнима - 2023, 11.6 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Смотрите, у нас есть условие, что AA1/BB1 = AC/BC. Обратите внимание на треугольники AA1C и BB1C. Что можно про них сказать?

Подсказка 2

Хочется сказать что они подобны, но у них общий угол BCA не между двумя соответственными сторонами. Тогда это почти как 4 признак равенства треугольников, только подобия: если растянуть один из треугольников так, что там две стороны будут равны, то выйдет как раз 4 признак равенства! Что это будет означать?

Подсказка 3

Это значит, что либо угол AA1C = BB1C, но это значит, что ABC - равнобедренный, а так нельзя. Остается, что AA1C + BB1C = 180. Что тогда можно сказать про угол BCA?)

Подсказка 4

Он равен 60! А теперь попробуйте посчитать периметр, вспомнив про то, что отрезок касательной из C к нашей вневписанной окружности - это полупериметр)

Показать ответ и решение

$PIC$

Докажем, что $∠BCA = 60∘$ . Для этого положим $∠BAC = α,∠ABC = β$ , $∠BCA = γ$ и воспользуемся теоремой синусов.

Имеем:

AA1-= ---AC---, BB1-=---BC--- , sinγ sin∠AA1C sinγ sin∠BB1C

откуда

-AA1= AC- ⋅ sin∠BB1C BB1 BC sin∠AA1C

С учетом условия $AA1 AC- BB1 = BC$ это означает, что $sin∠BB1C = sin∠AA1C$ . Равенству $α =β$ противоречит условие задачи.

Поэтому $β α ∘ α + 2 + 2 + β =180$ , откуда $∘ α +β =120$ и $∘ γ = 60$

Теперь найдем периметр треугольника $ABC$ . Пусть окружность с центром $O$ касается стороны $AB$ в точке $K$ , а продолжений сторон $CA$ и $CB$ - в точках $S$ и $T$ соответственно.

Тогда $AK =AS,BK = BT$ и

AB + CA +CB = CA + AS+ CB +BT = CS +CT = =OS ctg γ+ OTctg γ =2ctg30∘ =2√ 3 2 2

Ответ:

$2√3$

Ошибка.
Попробуйте повторить позже

Задача 13#63949

При каких значениях параметра $a$ система уравнений

({ -1-- -1-- logx3 + logy3 = 1; ( y =3 − ax

не имеет решений?

Источники: Миссия выполнима - 2023, 11.5 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Запишем одз и преобразуем первое уравнение по свойствам логарифма! Как можно теперь выразить y через x?

Подсказка 2

Если вышло, что log_3(xy) = 1, то все верно) Тут мы получаем, что xy = 3, то есть y = 3/x. Давайте подставим во второе уравнение. Какие значения а мы теперь должны найти?

Подсказка 3

Мы должны найти все такие а, что полученное уравнение не имеет положительных корней, которые отличаются от 1 и 3. Наше уравнение выглядит как 3/x = 3 - ax. Домножим на x и получим ax^2 -3x + 3 = 0. Какие случаи стоит рассматривать?

Подсказка 4

Для начала можем посмотреть на a = 0, тогда уравнение не квадратное. С этим случаем легко разобраться. Со случаем a!=0 вот что можно делать: либо у него нет корней, либо они есть, либо они отрицательные, либо положительные корни - 1 или 3)

Показать ответ и решение

Область допустимых значений переменных задается условиями

x> 0,x⁄= 1,y >0,y ⁄= 1.

Из первого уравнения получаем

log3x+ log3y = 1

откуда $xy = 3$ .

Подставив $y = 3x$ во второе уравнение, получим

ax2− 3x+ 3= 0

Мы должны найти все такие $a$ , при которых это уравнение не имеет положительных корней, отличных от 1 и 3.

Если $a= 0$ , то $x= 1$ единственный корень. Но $x⁄= 1$ .

Если же $a ⁄=0$ и дискриминант $D = 9$ - $12a$ отрицателен, то действительных корней нет вообще.

Итак при $a∈ {0}∪(34,+∞ )$ исходная система решений не имеет. При $a ≤ 34$ хотя бы один положительный корень у квадратного уравнения есть, поскольку сумма корней и их произведение имеют одинаковый знак. Если же один из корней равен 3, то $a = 23$ и уравнение $23x2− 3x+ 3= 0$ имеет также корень $x= 32$ , а исходная система имеет решение $(32;2).$

Ответ:

${0}∪(3,+∞ ) 4$

Ошибка.
Попробуйте повторить позже

Задача 14#63948

На поверхности правильного тетраэдра $ABCD$ построена замкнутая линия, каждая точка $X$ которой обладает следующим свойством: длина кратчайшего пути по поверхности тетраэдра между $X$ и серединой ребра $AB$ равна длине кратчайшего пути по поверхности тетраэдра между $X$ и серединой ребра $CD$ . Найдите длину этой линии, если длина ребра тетраэдра равна 1.

Источники: Миссия выполнима - 2023, 11.4 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

У нас тут рассматривается расстояние по поверхности...Как можно перевести картинку на плоскость в таком случае, чтобы было более удобно?

Подсказка 2

Рассмотреть развертку! Вот пусть мы развернули его так, что получился ромб ABCD, где AC - общее ребро у развернутых граней. Но все еще непонятно как работать с линиями ломаной, которые не получится нормально нарисовать на развертке. Что можно в таком случае придумать?

Подсказка 3

Давайте мысленно "порежем" нашу ломаную ребрами и отрезками AN, BN, CM, DM, где M и N - середины AB и CD, и рассмотрим только ту часть ломаной, что внутри треугольника AMC на нашей развертке. Наверное, в этом треугольнике не сложно найти такие точки на развертке?

Подсказка 4

Например, пусть P - точка ломаной внутри AMC. Понятно, что кратчайший путь от P до M - это PM, а кратчайший путь от P до N - это отрезок PN). Такие отрезки должны быть равны, а значит какое ГМТ у P?

Подсказка 5

Серединный перпендикуляр к MN! Достаточно легко теперь найти длину этой ломаной внутри AMC. А что делать с остальными частями этой ломаной? Вот что: попробуйте осознать, что они будут такими же, например, из соображений симметрии)

Показать ответ и решение

Пусть $M$ и $N$ — середины ребер $AB$ и $CD$ соответственно. Из соображений симметрии ясно, что ребрами $AC,BC, BD,AD$ и отрезками $AN, BN,CM, DM$ линия, о которой идет речь в условии задачи разбивается на 8 равных. Поэтому достаточно рассмотреть точки, принадлежащие треугольнику $AMC$ .

$PIC$

Пусть $P$ - одна из таких точек. Тогда кратчайшим путем между $P$ и $M$ служит отрезок $PM$ , а кратчайшим путем между $P$ и $N$ - двухзвенная ломаная $PKN$ , вершина $K$ которой принадлежит ребру $AC$ (в случае $P ∈AC$ имеем просто отрезок $PN)$ . На развертке тетраэдра объединение граней $ABC$ и $ADC$ представляет собой ромб $ABCD$ , а ломаная $PKN$ - отрезок $PN$ в нем. Условие $P M =P N$ означает, что $P$ лежит на серединном перпендикуляре к отрезку $MN$ ; следовательно геометрическим местом точек $P$ служит отрезок $QR$ , где $Q$ - середина ребра $AC$ (и середина отрезка $MN$ ) $R$ - точка на отрезке $MC$ , $∠MQR = 90∘$ (см рисунок).

Найдем длину отрезка $QR$ . Легко видеть, что $∠QMR = 30∘$ , а отрезок $QM$ , будучи средней линией треугольника $ABC$ , имеет длину $1 2$ . Поэтому $QR = 1tg30∘ = √3 2 6$

Умножив это число на 8, получим ответ к задаче: $4√3- 3$

Ответ:

$4√3 3$

Ошибка.
Попробуйте повторить позже

Задача 15#63947

Десятичная запись суммы $3 +33+ 333 +...+ 33...3$ оканчивается на $2023.$ Каким наименьшим может быть количество цифр в последнем слагаемом?

Источники: Миссия выполнима-2023, 11.3 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Подсказка 2

Она равна 3+33+333+3333(n-3), где n какое-то натуральное число. Как из этого выразить n через m?

Подсказка 3

Осталось понять, при каком минимальном m у нас найдётся такое n, выделив целую часть или посмотрев по модулю 3333)

Показать ответ и решение

Пусть в последнем слагаемом $n$ цифр. По условию десятичная запись суммы $3+ 33+333+ ...+ 33...3 ◟ ◝◜n-◞$ оканчивается на $2023:$

2023 ≡ 3+ 33 +333+ ...+3◟3.◝.◜.3◞ ≡ 3+ 33+ 333+ 3333(n − 3) 10000 n 10000

то есть при некотором натуральном $m$ верно

3+ 33 +333+ 3333(n − 3)= 2023 +10000m = 2023+ 3333⋅3m + m

2023− (3+-33+333)+m n= 3+ 3m+ 3333

откуда с учётом натуральности $m$ сразу следует условие для сократимости дроби

2023− (3 +33+ 333)+ m ≥3333 ⇐⇒ m ≥1679

Следовательно,

n≥ 3+ 3⋅1679+ 1= 5041

В обеих оценках достигается равенство, при котором выполнено условие.

Ответ: 5041

Ошибка.
Попробуйте повторить позже

Задача 16#63946

Решите уравнение

sin(cosx) =sin (1+ sinx)

Источники: Миссия выполнима - 2023, 11.2 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Равенство синусов...когда оно возможно?

Подсказка 2

Когда аргументы синуса равны или в сумме дают π! Так и запишем: cos(x) = 1 + sin(x) + 2πk. Пока не совсем понятно, как же работать с k...попробуем его оценить! Часто в работе с тригонометрическими функциями используют какие-то неравенства, оценки - быть может, и сейчас мы сможем как-то оценить 2πk = 1 + sin(x) - cos(x), чтобы как-то найти k? С помощью чего можно это сделать(учитывая, что сами тригонометрические функции оцениваются нетрудно: |sin(x)| <= 1, |cos(x)| <= 1)

Подсказка 3

С помощью модулей! Помним правило для модуля суммы: |a+b|<= |a|+|b|. Пробуем им воспользоваться, какую тогда оценку на |2πk|получим?

Подсказка 4

|2πk|<= |sin(x)| + |1| + |cos(x)| <= 3 <= 2π, тогда несложно найти k) Остаётся решить несложное тригонометрическое уравнение и не забыть про второй случай, вытекающий из подсказки 2!

Показать ответ и решение

Для данного равенства возможны два случая.

1.

$cosx= 1+ sinx+ 2πk,k ∈Z;$ при этом

|2πk|=|1+sinx− cosx|≤1 +|sinx|+ |cosx|≤1+ 1+ 1≤ 2π

Отсюда $k= 0$ . Далее,

cosx =1+ sinx

cosx− sinx =1

По формуле вспомогательного аргумента

( π) √2- cos x+ 4 = 2

x= − π4 ± π4 +2πn,n∈ Z

2.

$cosx+ 1+ sinx= π+ 2πk,k ∈Z$

Поскольку

|cosx+ 1+ sinx|≤|cosx|+ 1+ |sin x|≤ 1+ 1+ 1< π ≤|π+ 2πk|,

то в этом случае решений нет.

Ответ:

$− π ± π+ 2πn,n ∈ℤ 4 4$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#63945

Фитнес-центр продал 515 годовых абонементов, базовая цена каждого из которых составляла 8000 рублей. При этом каждый $m$ -й продаваемый абонемент был акционный и продавался со скидкой, равной 1000 руб. Покупатель каждого четвертого акционного абонемента получал, сверх того, и дополнительную скидку в размере 1500 руб. Определите число $m$ , если итоговая выручка фитнес-центра от продажи абонементов составила 3 979 500 руб.

Источники: Миссия выполнима - 2023, 11.1 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

В данной задаче проще считать не сумму, потраченную на покупку абонементов, а сумму скидок. Чему она равна?

Подсказка 2

Сумма скидок это 515*8000-3979500. Теперь остаётся лишь посчитать её другим способом и составить уравнение...

Подсказка 3

Будем рассматривать только абонементы со скидкой. Пусть со скидкой 1000+1500=2500 было продано x абонементов. Сколько тогда было продано со скидкой 1000?

Подсказка 4

Тогда со скидкой 1000 было продано "примерно в три раза больше", а если строго, то 3x+r, где r это 0, 1, 2 или 3. Теперь составляем уравнение в целых числах и находим из него x и r.

Подсказка 5

Как теперь найти m? Для этого достаточно найти количество всех билетов со скидкой 1000 и...

Подсказка 6

Разделить 515 на это количество.

Показать ответ и решение

Пусть $x$ — количество абонементов, проданных с максимальной ( $1000 +1500= 2500$ pуб.) скидкой. Количество остальных акционных абонементов тогда выражается формулой $3x+ r$ , где $r ∈{0,1,2,3}$ . При этом общая сумма скидок, равная $2500x +1000(3x+ r)= 5500x+ 1000r$ (руб.), равна с другой стороны $515 ⋅8000− 39795000 =140500$ (руб.)

Уравнение $5500x+ 1000r =1405000$ при $r= 0,1,2$ не имеет целых корней, а при $r= 3$ получается $x= 25.$ Искомое $m$ теперь находим как частное от деления 515 на $25+ 3⋅25+3 =103.$

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 18#76733

Докажите, что для любого натурального $n$ существует натуральное число, которое больше своей суммы цифр в $11...11 ◟--◝◜n-◞$ раз.

Источники: Миссия выполнима-2022, 10.1 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Для каких чисел проще всего проверить делимость на число, состоящее из одних единиц?

Подсказка 2

Для чисел, состоящих из одинаковых цифр, или тех, которые получаются из вышесказанных домножением на какое-нибудь число. Попробуем найти такое число, полученное из числа, состоящего из девяток.

Подсказка 3

Найдите число с суммой цифр 9n, удовлетворяющее требованием из предыдущих подсказок.

Показать доказательство

Рассмотрим десятичную запись числа $n(10n − 1).$ Пусть число $n$ оканчивается на $k$ нулей. Если последняя ненулевая цифра числа $n$ равна $x$ , то у числа $n n(10 − 1)$ последняя ненулевая цифра будет $10 − x.$ Если предпоследняя цифра $y$ , то у числа $n n(10 − 1)$ предпоследняя цифра будет $9− y$ и т.д. А в начале числа $n n(10 − 1)$ будут идти цифры числа $n$

$PIC$

Далее легко видеть, что сумма цифр $n(10n − 1)$ будет равна $9n$ .

Таким образом, условию удовлетворяет число $n(10n− 1)$ .

Ошибка.
Попробуйте повторить позже

Задача 19#76536

Число $a >0$ таково, что неравенства $2≤ an ≤ 4$ выполняются ровно при $5$ натуральных значениях $n.$ При скольких натуральных значениях $n$ могут выполнятся неравенства $n 4≤a ≤8?$

Источники: Миссия выполнима-2022, 11.7 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Пользоваться изначальным неравенством, где n стоит в показателе степени, неудобно. Предположим logₐ 2 = 𝜶 и зададим обычные ограничения на n. Если при заданном а значений n ровно 5, то как можно записать это в виде неравенства?

Подсказка 2

Верно, числа от n до n+4 принадлежат промежутку от 𝜶 до 2𝜶, при этом n-1 уже меньше 𝜶, а n+4 больше 2𝜶. Теперь попробуем преобразовать наше неравенство так, чтобы "зажать" и найти количество значений n, лежащих в промежутке от 2𝜶 до 3𝜶.

Подсказка 3

И не забудьте для каждого количества решений привести примеры!

Показать ответ и решение

Ясно, что $a> 1.$ Полагая $log 2= α, a$ неравенство $2≤an ≤4$ перепишем в виде $α≤ n≤ 2α,$ а неравенства $4≤ an ≤8$ - в виде $2α ≤n ≤3α.$ Согласно условию, для некоторого натурального числа $m$ выполнены неравенства $m − 1 <α ≤ m< m + 4≤2α <m + 5.$ Из них следует, что

2m − 2< 2α ≤2m < 2m +3< 3α< 2m +5.

Таким образом, неравенствам $2α ≤n ≤3α$ обязательно удовлетворяет четвёрка чисел ${2m;2m +1;2m+ 2;2m + 3}$ и, возможно , одно или оба числа пары ${2m − 1;2m +4}.$

Приведём три соответствующих примера. При $α= 4,6$ имеем $m =5$ и

2m − 1 <2α <3α <2m + 4;

при $α= 5,2$ имеем $m =6$ и выполняются неравенства

2α< 2m − 1 <3α <2m + 4;

наконец, если $α =5,4,$ то $m =6$ и

2α< 2m − 1 <2m + 4< 3α.

Ответ: четыре, пять или шесть

Ошибка.
Попробуйте повторить позже

Задача 20#76535

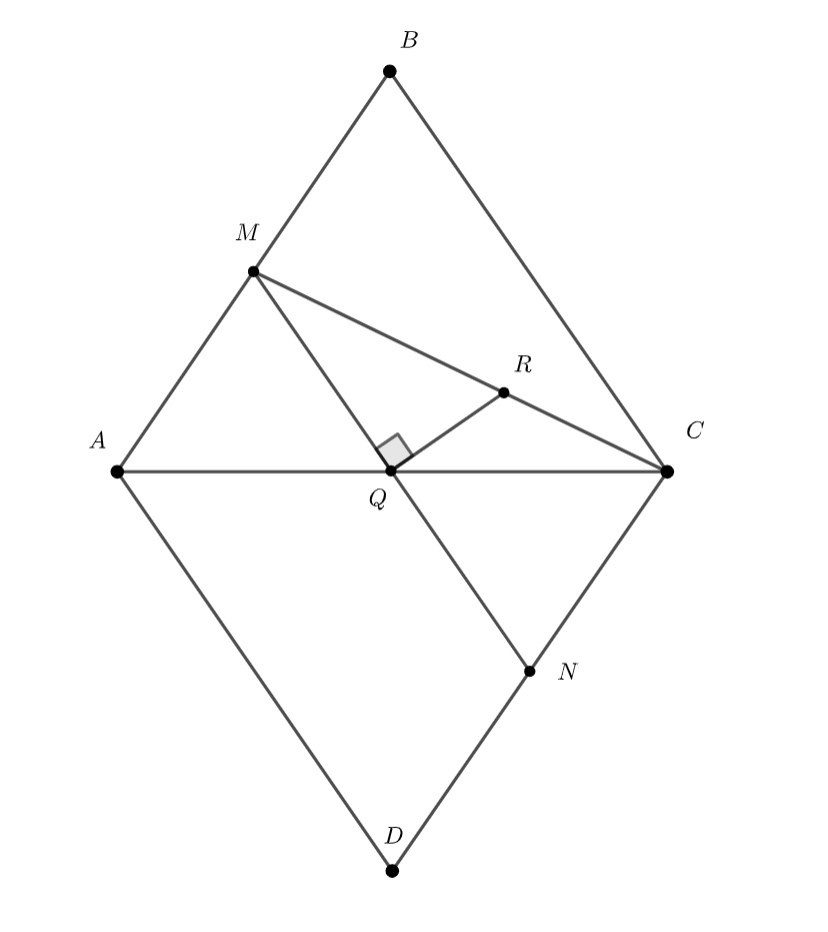
На сторонах $BC,$ $CA$ и $AB$ неравнобедренного треугольника выбраны точки $L,$ $M$ и $N$ соответственно. Биссектриса угла $ABC$ и серединный перпендикуляр к отрезку $NL$ пересекаются в точке $P.$ Известно, что $∘ ∠ABC =135 ,AN =NM = ML = LC = 1$ Найдите длину отрезка $MP.$

Источники: Миссия выполнима-2022, 11.6 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

По условию треугольники AMN и MLC – равнобедренные, значит, ∠NMA = ∠BAC, а также ∠LMC = ∠BCA, что тогда можно сказать про величину угла NML? Также подумайте, как этот угол может нам помочь в дальнейшем решении.

Показать ответ и решение

$PIC$

Так как из условий $AN = NM =ML =LC$ следуют равенства $∠AMN =∠BAC$ и $∠CML = ∠BCA$ соответственно, то

∠LMN = 180∘ − ∠AMN − ∠CML = 180∘− ∠BAC − ∠BCA = ∠ABC.

Заметим, далее, что точка $P$ лежит на описанной окружности треугольника $△NBL$ (и делит пополам дугу $NL,$ не содержащую $B$ ). Поэтому

∠LPN = 180∘− ∠ABC = 180∘− ∠LMN

с учётом того, что $P$ и $M$ лежат в одной полуплоскости относительно прямой $LN,$ заключаем, что $P$ - ортоцентр треугольника $△LMN.$

Рассмотрим теперь треугольник $△LP M.$ Используя равенства

∘ ∘ ∠LMN = 135 ,∠LP N = 45

и равнобедренность треугольника $△LP N,$ нетрудно найти углы $∠PLM = 45∘$ и $∠LP M = 22,5∘.$ Применив теорему синусов, получим $-MP-- -ML--- sin45∘ = sin22,5∘,$ откуда

∘ ∘ 1+-cos45∘- ∘---√-- MP = 2cos22,5 = 2 ---2----= 2 + 2

Ответ:

$∘2-+-√2$

Предыдущий раздел

Следующий раздел