Ошибка.
Попробуйте повторить позже
Объем куба равен . Найдите его диагональ.
![]()
Заметим, что объем куба равен , где
— длина ребра, а диагональ куба
равна
По условию . Тогда
Ошибка.
Попробуйте повторить позже
Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
![]()
Пусть длина ребра куба равна . Тогда его объём равен
. Если каждое ребро увеличили в 3 раза, то объём
стал равен
Значит, объём увеличился в 27 раз.
Ошибка.
Попробуйте повторить позже
Объём куба равен 8. Найдите площадь его поверхности.
![]()
Пусть длина ребра куба равна объем куба равен
Тогда имеем:
Площадь поверхности куба равна сумме площадей всех его граней. Площадь каждой из шести граней куба равна
Тогда площадь поверхности равна
Ошибка.
Попробуйте повторить позже
Найдите площадь поверхности куба, если его диагональ равна
Диагональ куба в раз больше его стороны, тогда сторона куба равна
Вычислим площадь боковой поверхности
Ошибка.
Попробуйте повторить позже
В кубе найдите угол между прямыми
и
Ответ
дайте в градусах.
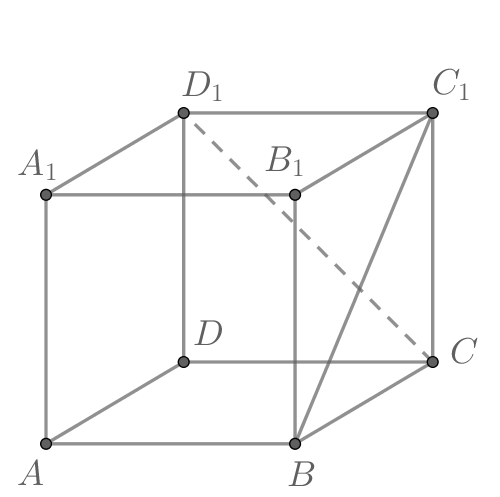
Так как то
Рассмотрим
Его стороны — диагонали одинаковых квадратов, следовательно, этот
треугольник равносторонний. Значит, все его углы равны по
то есть
Ошибка.
Попробуйте повторить позже
Через диагонали противоположных боковых граней куба провели плоскость. Найдите объём куба, если площадь полученного
сечения равна .
В кубе провели диагонали
и
противоположных граней
и
По условию
площадь сечения
равна
![]()
Если сторона куба равна то диагональ любой грани равна
Значит, площадь сечения равна
Тогда объем куба равен
Ошибка.
Попробуйте повторить позже
Число, соответствующее количеству кубических сантиметров объема куба, совпадает с числом, соответствующим количеству квадратных сантиметров площади поверхности куба. Найдите объем куба, выраженный в кубических миллиметрах.
Если ребро куба обозначить за , то
. Площадь поверхности куба равна сумме
площадей всех его граней. Все грани между собой равны и являются квадратами. Таких
граней в кубе будет
. Тогда
. Согласно условию задачи:
.
Тогда
Ошибка.
Попробуйте повторить позже
Дан куб .
– середина стороны
,
– середина стороны
,
.
Найдите площадь плоскости сечения, проходящей через точки
,
и
.
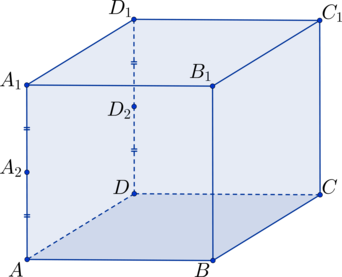
– фигура сечения куба.
– параллельна
и
, т.к. соединяет середины
и
, поэтому перпендикулярна граням
и
перпендикулярна
и
.
– прямоугольник.
Ошибка.
Попробуйте повторить позже
Анатолий грабит банк. Слитки золота имеют форму прямоугольных параллелепипедов с измерениями
. Сумка, которая есть у Анатолия, имеет форму куба с ребром длины
. Анатолию нужно
уложить как можно больше слитков в сумку так, чтобы она закрылась и с ней можно было выйти, не
привлекая к ней внимания. Сколько слитков сможет вынести Анатолий, если будет действовать
разумно?
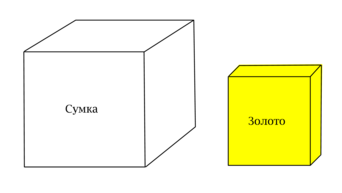
Сначала заметим, что ответ не изменится, если уменьшить масштаб в два раза по каждому
направлению. При этом сумка станет кубом с ребром , а слитки золота станут прямоугольными
параллелепипедами с измерениями
.
Оценим возможное количество слитков сверху: так как объём сумки равен , а объём
слитка равен
, то более
слитков в сумку не войдут. Но могут ли войти в неё
6?
Назовём слиток горизонтальным, если две его грани параллельны дну сумки так, что его высота
равна 1. В противном случае назовём слиток вертикальным. Мысленно “расслоим”сумку на 3
одинаковых горизонтальных слоя.
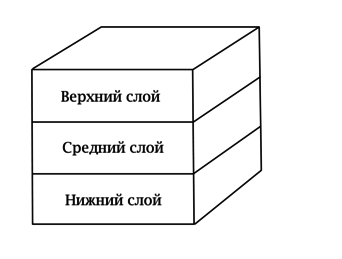
Каждый вертикальный слиток занимает в среднем слое по 2 соседних кубика с ребром 1. Средний слой состоит из 9 таких кубиков, следовательно, вертикальных слитков в сумку входит не более 4. При этом горизонтальных слитков в сумку входит не более 3 (в каждый слой входит не более одного горизонтального слитка).
В случае, когда горизонтальных слитков ровно 3, получим, что в среднем слое 4 кубика из 9
заняты горизонтальным слитком, то есть в среднем слое остаётся кубиков, но
каждый вертикальный слиток должен занимать в среднем слое по 2 кубика, тогда получаем,
что вертикальных слитков при этом не более 2 и всего слитков при трёх горизонтальных
.
Таким образом, последний шанс Анатолия унести 6 слитков – это 4 вертикальных слитка и 2
горизонтальных. Возможно ли это? Понятно, что для этого необходимо, чтобы горизонтальные слитки
лежали в нижнем и верхнем слоях, но верхний слиток не должен “полностью нависать”над нижним.
Тогда остаётся всего 2 принципиально различных способа уложить горизонтальные слитки в верхнем и
нижнем слоях относительно друг друга.
При этом один из них позволяет уложить 6 слитков. Чтобы наглядно проиллюстрировать его сначала
поместим в сумку только вертикальные слитки и покажем вид сверху:
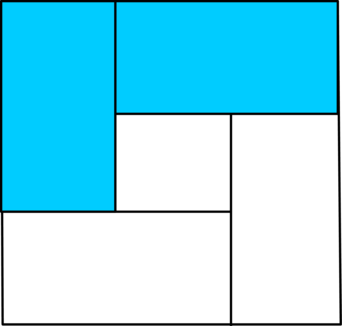
здесь голубым отмечены все те вертикальные слитки, которые стоят на дне сумки. Тогда на дно можно подложить ещё 1 горизонтальный слиток под те вертикальные, которые не стоят на дне сумки. Аналогично, в верхний слой можно подложить 1 горизонтальный слиток.
Итого: при разумном подходе Анатолий может вынести 6 слитков.
Ошибка.
Попробуйте повторить позже
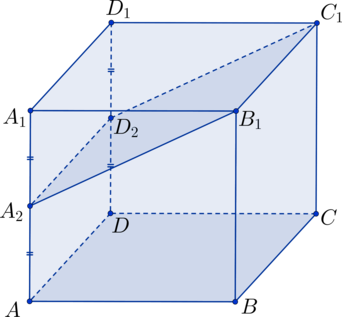
– куб с длиной ребра равной
. Точка
лежит на ребре
так, что
. Найдите площадь сечения куба, проведённого через точку
и ребро
.
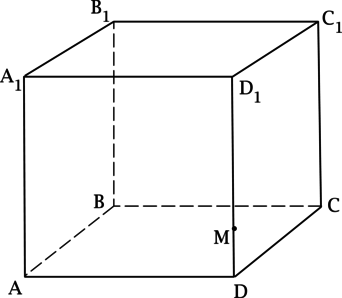
Пусть – точка на
, такая что
, тогда
, следовательно,
сечение, проходящее через точку
и ребро
– четырёхугольник
, причём
, следовательно,
. Аналогично
, то есть
–
прямоугольник.
Ошибка.
Попробуйте повторить позже
В кубе : точки
,
,
,
лежат соответственно на ребрах
,
,
и
, причем
,
. Найдите площадь
, если
.
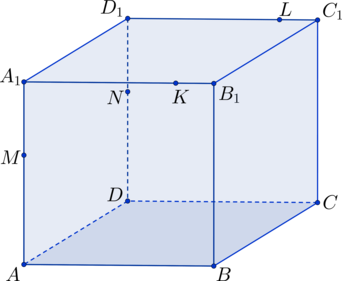
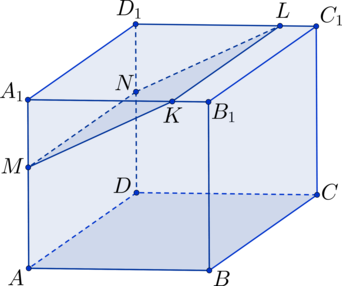
;
, т.к.
– параллелограмм
,
. Аналогичным образом получается, что
и
– параллелограмм, а т.к.
перпендикулярна граням
и
, то и
и
перпендикулярны этим же граням
– прямоугольник. Чтобы найти площадь этого
прямоугольника, найдем сперва сторону
из прямоугольного треугольника
, используя
теорему Пифагора.
Ошибка.
Попробуйте повторить позже
В кубе точки
и
– середины соответственно сторон
и
. Найдите
площадь поверхности фигуры
, если ребро куба равно
.
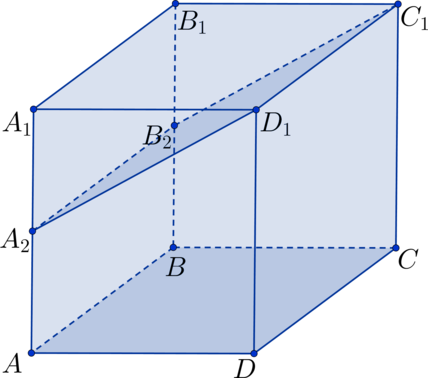
Площадь поверхности фигуры состоит из суммы следующих площадей:



