Комбинированные тела: их объемы и площади поверхностей —Каталог задач по ЕГЭ - Математика

Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Комбинированные тела: их объемы и площади поверхностей

Тема 3. Геометрия в пространстве (стереометрия)

3.15 Комбинированные тела: их объемы и площади поверхностей

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела геометрия в пространстве (стереометрия)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#2189

Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.

$PIC$

Показать ответ и решение

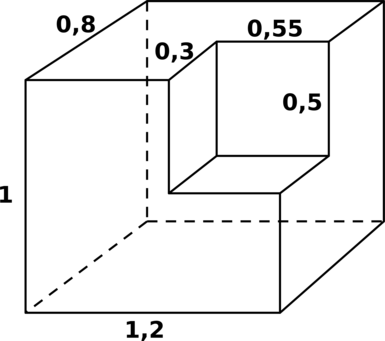
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен

0,8 ⋅ 1 ⋅ 1,2 − 0,3 ⋅ 0,5 ⋅ 0, 55 = 0,8775.

Ответ: 0,8775

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#1004

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

$PIC$

Показать ответ и решение

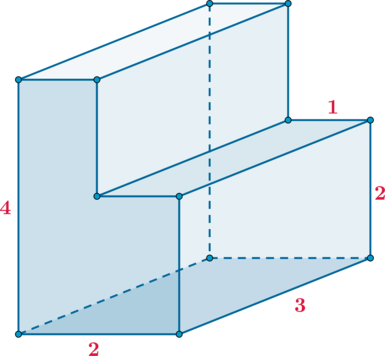
Заметим, что можно разбить данный многогранник на два непересекающихся прямоугольных параллелепипеда $ABCDA1B1C1D1$ и $DCEF D2C2E1F1$ :

$PIC$

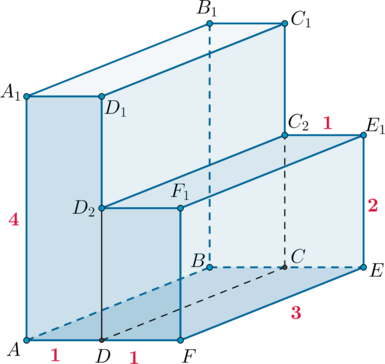
Тогда объем первого параллелепипеда будет равен $1 ⋅ 3 ⋅ 4 = 12$ , а объем второго $1 ⋅ 3 ⋅ 2 = 6$ . Следовательно, объем всего многогранника будет равен $12 + 6 = 18$ .

Ответ: 18

Ошибка.
Попробуйте повторить позже

Задача 3#75421

Найдите объём многогранника (все углы прямые), изображенного на рисунке.

$PIC$

Показать ответ и решение

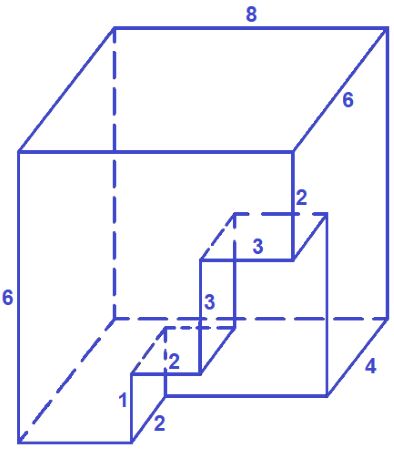
Найдём объём многогранника как разность объёмов большого параллелепипеда (с высотой 6) и суммы объёмов двух маленьких параллелепипедов (с высотами $1 + 3 = 4$ и 1):

V = 6 ⋅8⋅6− (1⋅2 ⋅2+ 4⋅3 ⋅2) = 260.

Ответ: 260

Ошибка.
Попробуйте повторить позже

Задача 4#18445

Из единичного куба вырезана правильная четырёхугольная призма со стороной основания 0,6 и боковым ребром 1. При этом центры нижних оснований призмы и куба совпадают. Найдите площадь поверхности оставшейся части куба.

Показать ответ и решение

Сначала вычислим площадь поверхности $S$ куба с ребром 1. Если $S1$ — площадь одной грани куба, то $S = 6 ⋅S1 = 6$ .
Найдем и вычтем площади верхнего и нижнего оснований призмы:

S2 = 2 ⋅0,6 ⋅0,6 = 0,72

S − S2 = 6 − 0,72 = 5,28

Найдем и прибавим площади боковых граней призмы:

S3 = 4⋅1⋅0,6 = 2,4

S + S3 = 5,28+ 2,4 = 7,68

Тогда площадь поверхности оставшейся части куба равна 7,68.

$PIC$

Ответ: 7,68

Ошибка.
Попробуйте повторить позже

Задача 5#17161

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

$PIC$

Показать ответ и решение

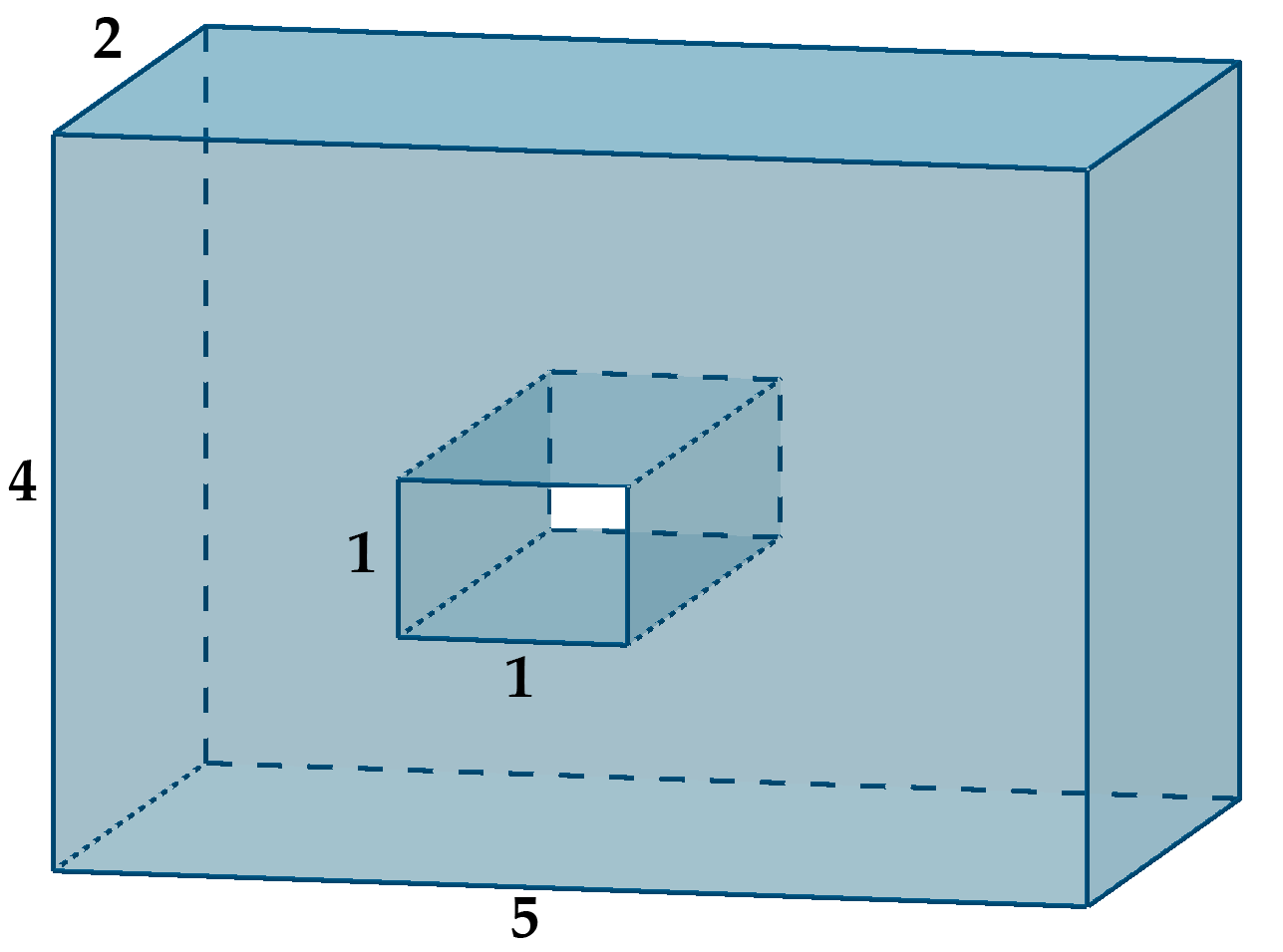
Найдем площадь поверхности большого прямоугольного параллелепипеда. Он имеет две грани с площадью $4 ⋅5,$ две грани с площадью $4⋅2$ и две грани с площадью $2⋅5.$ Следовательно, площадь его поверхности равна

2(4⋅5 +4 ⋅2+ 2⋅5)= 76

Из этого параллелепипеда вырезали прямоугольный параллелепипед с ребрами 1, 1 и 2. В результате этого площадь боковой поверхности уменьшилась на $2 ⋅(1 ⋅1)$ и увеличилась на $4 ⋅(1⋅2).$ Следовательно, площадь поверхности многогранника, изображенного на рисунке, равна

76 − 2 +8 = 82

Ответ: 82

Ошибка.
Попробуйте повторить позже

Задача 6#11714

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,6 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

$PIC$

Показать ответ и решение

Площадь поверхности равна сумме четырёх «внешних» вертикальных граней, четырёх «внутренних» вертикальных граней и оставшихся после выреза частей двух горизонтальных граней. Тогда имеем:

S = 4⋅(1⋅1)+4 ⋅(0,6⋅1)+ 2⋅(1 ⋅1 − 0,6⋅0,6)= =4 +2,4+ 1,28= 7,68

Ответ: 7,68

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#2715

Точка $A$ – середина оси цилиндра, высота которого $h$ . Точка $B$ лежит на основании цилиндра (с центром $O$ и радиусом $R$ ), причём угол между $AB$ и плоскостью основания равен $60∘$ , Объём заштрихованной области

75√5-- V штрих = -√---. π

Найдите площадь боковой поверхности конуса с вершиной $A$ и основанием, совпадающим с основанием цилиндра.

$PIC$

Показать ответ и решение

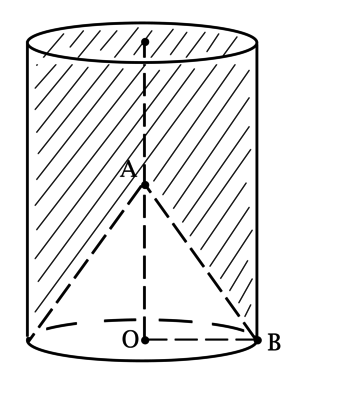
Рассмотрим прямоугольный треугольник $AOB$ : $AO = 0,5h$ , $∠ABO = 60∘$ , $OB = R$ , тогда $∘ √ -- 0,5h = R ⋅ tg60 = R 3$ , откуда $√ -- h = 2R 3$ ; $---R--- AB = cos 60∘ = 2R$ .

√ -- √ -- 75√--5-= V = V − V = πR2h − 1-πR2 ⋅ 0, 5h = πR2 ⋅ 5h-= πR3 5--3, π ш трих цил кон 3 6 3

тогда $√ -- √ -- 75---5 35--3- √ π- = πR 3$ , откуда $∘ --- 15- R = π$ , тогда

2 Sбок кон = πR ⋅ AB = 2πR = 30.

Ответ: 30

Ошибка.
Попробуйте повторить позже

Задача 8#1891

Песочные часы состоят из двух одинаковых усеченных конусов, плоскости оснований которых параллельны. Высота песочных часов $H = 16$ . Радиус окружности, являющейся пересечением боковых поверхностей конусов, равен $1$ . Тангенс половины угла раствора каждого конуса равен $1 2$ . Найдите объем песочных часов $V$ , умноженный на $3 π$ .

$PIC$

Показать ответ и решение

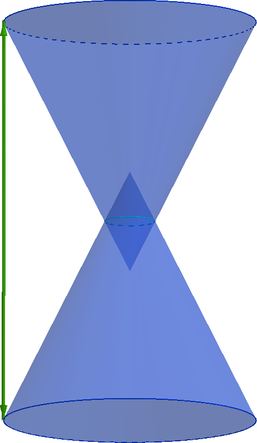
Выберем какое-нибудь сечение конусов плоскостью $α$ , проходящей через их общую ось вращения.

$PIC$

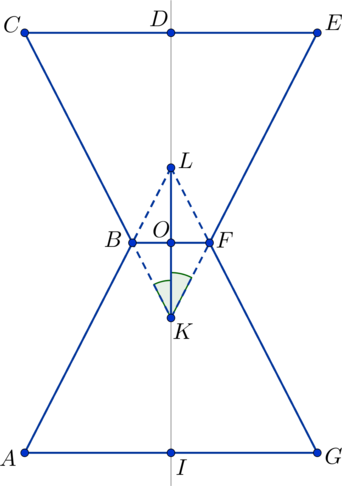
На рисунке в плоскости $α$ : $DI$ – ось вращения конусов, отрезок $DI$ совпадает с высотой песочных часов и равен $16$ . Отрезки $CD$ и $DE$ являются радиусами окружности, лежащей в верхнем основании фигуры, а отрезки $BO$ и $OF$ являются радиусами окружности пересечения конусов, поэтому $BO = OF = 1$ . Угол раствора конуса $∠CKE$ делится пополам осью вращения на равные углы $∠CKD$ и $∠DKE$ , поэтому $tg∠CKD = tg∠DKE = 12$ . Рассмотрим $△CKD$ и $△BKO$ . Плоскости оснований конусов и плоскость, содержащая окружность пересечения конусов, параллельны друг другу $⇒$ рассматриваемая плоскость сечения $α$ будет пересекать эти плоскости по прямым, параллельным друг другу $⇒$ $CD ||BO$ $⇒$ $△CKD$ и $△BKO$ подобны друг другу $⇒$ $CD- KD- BO = KO$ . Ось вращения перпендикулярна плоскостям оснований и плоскости пересечения конусов $⇒$ $△CKD$ и $△BKO$ – прямоугольные треугольники. Т.к. $DI = H$ $⇒$ $DO = OI = H : 2 = 8$ ; $KO = BO : tg ∠CKD = 1 : 1 = 2 2$ $⇒$ $KD = KO + OD = 2 + 8 = 10$ $⇒$ $CD-= KD- = 10 = 5 BO KO 2$ $⇒$ $CD = 5$ .

Объем усеченного конуса $CBOF EDC$ можно посчитать как разность объемов конуса $KCDE$ и конуса $KBOF$ :

VCBOF EDC = VKCDE − VKBOF = 1⋅πCD2 ⋅KD − 1⋅πBO2 ⋅KO = 1-⋅π⋅ 52 ⋅10 − 1-⋅π ⋅12 ⋅2 = 248π-. 3 3 3 3 3

Объем песочных часов складывается из двух объемов усеченного конуса, т.к. ситуация с нижним конусом полностью аналогична ситуации с верхним конусом в силу симметрии задачи, поэтому их объемы совпадают $CBOF EDC$ объем песочных часов равен $248π- 2 ⋅ 3$ . Окончательно, после умножения на $3π$ получаем:

V = 496.

Ответ: 496

Ошибка.
Попробуйте повторить позже

Задача 9#1888

Дан куб $ABCDA1B1C1D1$ . Точка $B2$ лежит на продолжении ребра $BB1$ за точку $B1$ , $BB2 = 2 ⋅ BB1$ . Во сколько раз объем куба отличается от объема пирамиды $B2ABCD$ ?

$PIC$

Показать ответ и решение

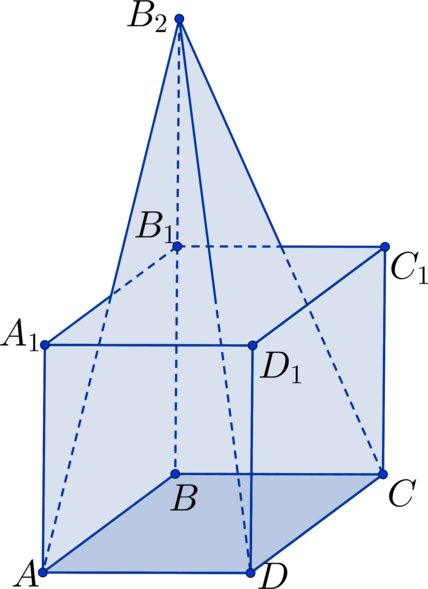
Отрезок $BB2$ является высотой пирамиды. Если сторону куба обозначить за $x$ , то $BB2 = 2x$ $⇒$

1- 1- 2 2- 3 3 V пир. = 3 ⋅ BB2 ⋅ SABCD = 3 ⋅ 2x ⋅ x = 3 ⋅ x ,Vкуб = x .

Теперь найдем искомую величину:

V куб x3 -----= 2---3-= 1,5. Vпир. 3 ⋅ x

Ответ: 1,5

Ошибка.
Попробуйте повторить позже

Задача 10#586

Верхняя грань куба является основанием пирамиды, высота которой равна $4$ . Найдите площадь поверхности фигуры, если сторона квадрата равна $6$ .

Показать ответ и решение

$PIC$

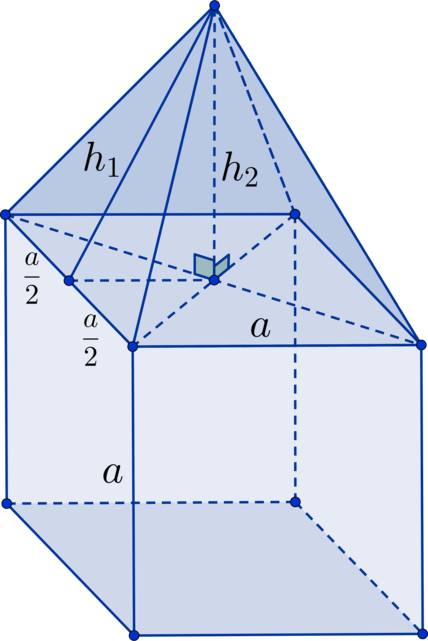
Найдем сперва апофему пирамиды $h1$ из прямоугольного треугольника, в котором она является гипотенузой, а катеты – это высота пирамиды $h2$ и половина стороны квадрата $a- 2$ : $2 2 a2- h1 = h2 + 4$ $⇒$ $2 36 h 1 = 16 + 4--$ $⇒$ $h1 = 5$ . Площадь боковой грани пирамиды: $1 1 2ah1 = 2-⋅ 6 ⋅ 5 = 15$ . Площадь грани куба: $a2 = 36$ . Площадь поверхности фигуры состоит из пяти граней куба и четырех боковых граней пирамиды: $S = 5 ⋅ 36 + 4 ⋅ 15 = 180 + 60 = 240$ .