Ошибка.
Попробуйте повторить позже
Основанием правильной треугольной пирамиды является треугольник
при этом
Через точку
перпендикулярно апофеме грани
проведена плоскость
а) Докажите, что плоскость делит апофему грани
в отношении
считая от точки
б) Найдите угол между прямой и плоскостью
Источник:
а) Так как пирамида правильная, то в основании лежит правильный треугольник
а основание высоты этой пирамиды — центр
этого треугольника. Пусть
Тогда
и по теореме о трех
перпендикулярах
Следовательно,
— апофема грани
Проведем а через точку
проведем
Тогда
Докажем, что
Пусть Тогда
Пусть Тогда
Следовательно,
Значит,
Что и требовалось доказать.
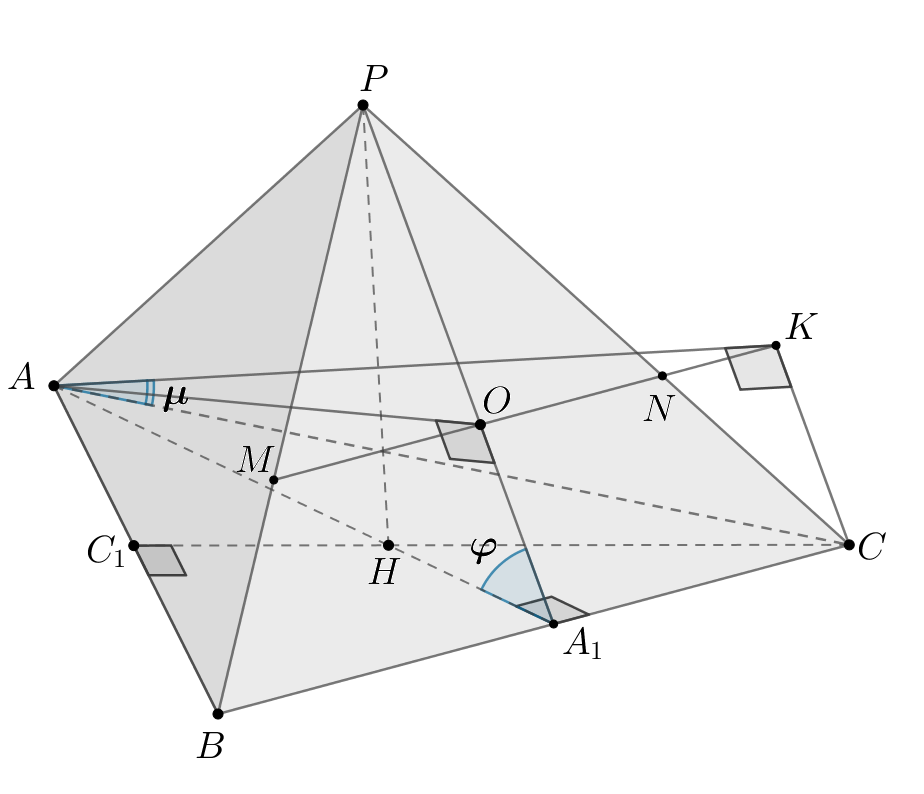
б) Проведем как показано на рисунке. Тогда
следовательно,
— проекция наклонной
на плоскость
Так как угол
между прямой и плоскостью — это угол между прямой и ее проекцией на эту
плоскость, то нужно найти
— прямоугольный с прямым углом
Следовательно,
Так как то
следовательно, расстояние от любой точки
прямой
до плоскости
одинаково, откуда следует, что
Значит,
б)
Ошибка.
Попробуйте повторить позже
На ребрах и
правильной треугольной призмы
отметили
соответственно точки
и
так, что
и
Через точки
и
параллельно прямой
проведена плоскость
а) Докажите, что точка пересечения плоскости с ребром
является
серединой отрезка
б) Найдите площадь сечения призмы плоскостью
если
Источник:
а) Проведем Отметим на
точку
так, что
Тогда
— параллелограмм, откуда
Следовательно,
Пусть Тогда так как
то
Следовательно,
Следовательно,
По теореме Менелая для и прямой
Следовательно, точка — середина отрезка
Что и требовалось
доказать.
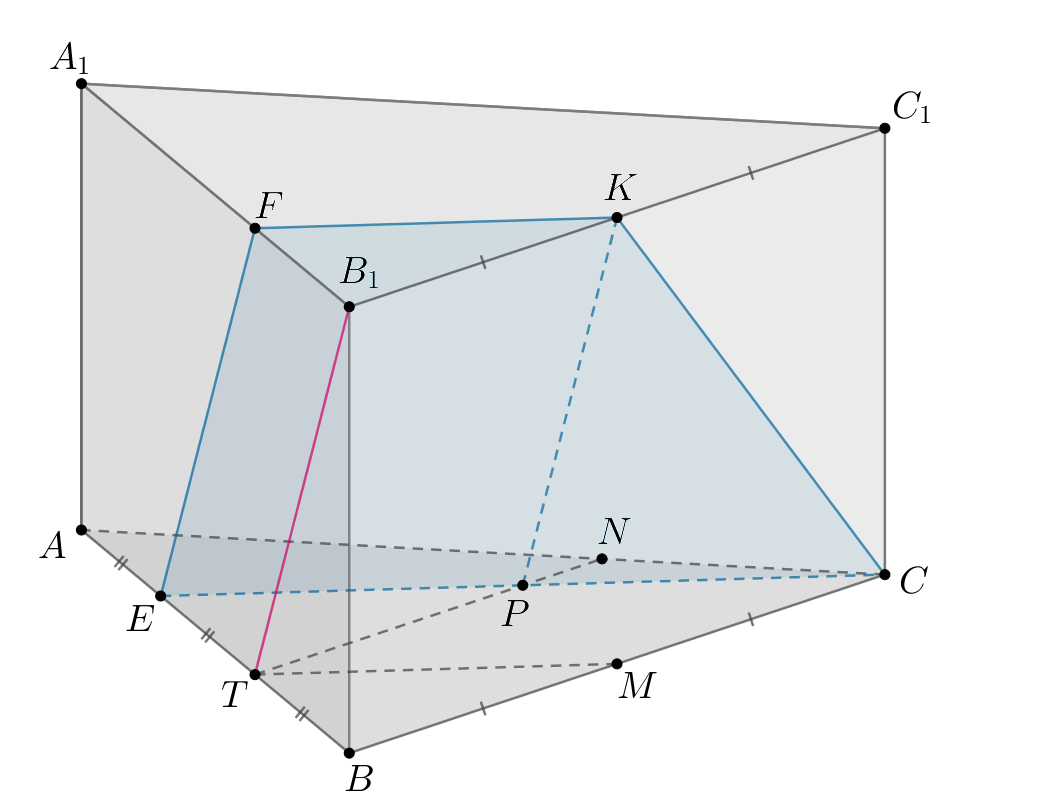
б) Так как секущая плоскость пересекает параллельные плоскости по
параллельным прямым, то Значит, сечение
— трапеция
(заметим, что
)
Пусть — середина
Тогда
— средняя линия в
значит,
Но так как то
Тогда так как точки
и
—
середины
и
соответственно, то
Так как то
Следовательно, так как
то
Значит,
— параллелограмм, значит,
Следовательно, — середина
По теореме косинусов для
Таким образом,
Тогда
Также имеем:
Следовательно, по теореме косинусов для имеем:
Таким образом,
Путь Тогда
— высота сечения. Из
Значит, искомая площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием четырехугольной пирамиды является квадрат
при
этом ребро
перпендикулярно плоскости основания. Через середины ребер
и
параллельно прямой
проведена плоскость
а) Докажите, что точка пересечения плоскости с ребром
делит его в
отношении
считая от вершины
б) Найдите площадь сечения пирамиды плоскостью
если
Источник:
а) Проведем диагонали основания и
пересекающиеся в точке
а
также отметим точки
и
— середины ребер
и
соответственно.
Тогда
Рассмотрим плоскость Прямая
пересекает эту плоскость в точке
лежащей на отрезке
Проведем через точку
отрезок
Тогда
Следовательно,
Значит, требуется
доказать, что
Так как — средняя линия в
то
Тогда по
теореме Фалеса
откуда следует, что
— середина
Значит,
А так как
то теореме Фалеса
Что и требовалось доказать.
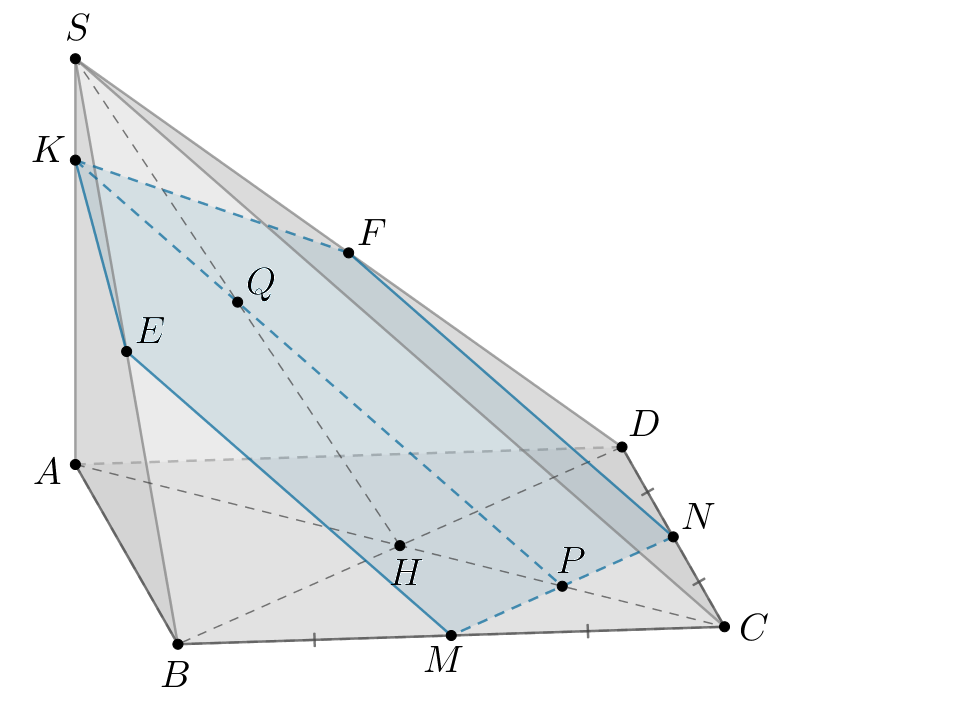
б) Пусть Так как плоскость
проходит через
и
то
Следовательно, плоскость
пересекает плоскость
по прямой
проходящей через точку
и параллельной
Тогда
— сечение пирамиды плоскостью
Так как
то по теореме о трех перпендикулярах
Значит, так как
то верно следующее:
Также, так как
то
пересечет плоскости, в которых
лежит
по прямым, параллельным
Значит,
Следовательно, сечение состоит из двух многоугольников: прямоугольника
и равнобедренного
(ребра
и
равны, так как равны
прямоугольные
и
; по теореме Фалеса
и
— середины
и
соответственно, значит,
).
Найдем необходимые длины отрезков:
Тогда
б) 12,5
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием четырехугольной призмы является прямоугольная
трапеция
в которой
а основания
и
соответственно равны
и
а) Докажите, что если то объемы многогранников, на которые призму
делит плоскость
относятся как
б) Объемы многогранников и
на которые призму
делит плоскость
соответственно равны 30 и 20.
Найдите высоту призмы
если
Источник:
а) Обозначим
— высота призмы. Тогда объем призмы
равен
Проведем
Тогда
— призма, в
основании которой лежит прямоугольник, а высота этой призмы равна
Следовательно, ее объем равен
Пусть
Тогда
Тогда получаем
Значит,
— треугольная пирамида, высота которой, проведенная из вершины
равна
Следовательно, ее объем равен
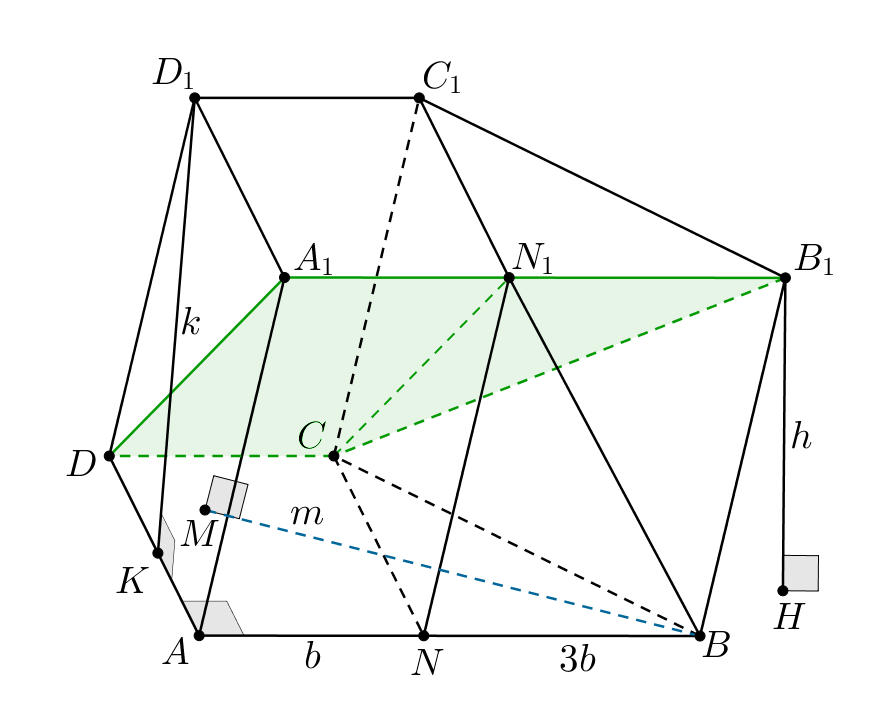
Следовательно, объем многогранника образованного
плоскостью
равен
Тогда объем оставшейся части равен
Следовательно,
Что и требовалось доказать.
б) Пусть
Определим, возможен ли такой случай, учитывая
данные. Этому случаю соответствует рисунок, приведенный в решении пункта а).
Используя обозначения пункта а), получаем
Тогда
Следовательно,
Следовательно, этот случай невозможен, так как
Пусть
Проверим возможность такого случая. Рассмотрим
рисунок, соответствующий этому случаю:
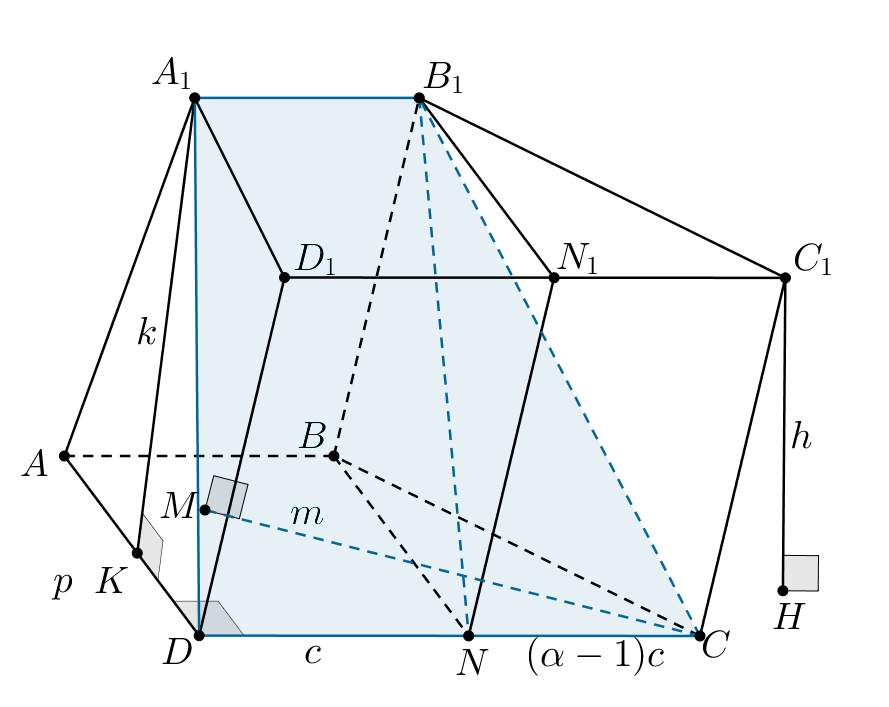
Тогда
Этот случай является единственно возможным.
По условию
Следовательно,
Тогда можем найти высоту призмы:
б) 4
Ошибка.
Попробуйте повторить позже
В основании пирамиды лежит трапеция
с большим основанием
Диагонали трапеции пересекаются в точке
Точки
и
— середины
боковых сторон
и
соответственно. Плоскость
проходит через точки
и
параллельно прямой
а) Докажите, что сечение пирамиды плоскостью
является
трапецией.
б) Найдите площадь сечения пирамиды плоскостью
если
а прямая
перпендикулярна прямой
Источник:
а) Пусть пересекает диагонали
и
в точках
и
соответственно.
Так как
то
пересечет плоскости, в которых находится
по
прямым, параллельным
Следовательно, проведем в плоскостях
и
прямые
(см.рис.). Получим сечение пирамиды
плоскостью
— четырехугольник
Так как то
следовательно,
пересечет плоскость
в которой лежит
по прямой, параллельной
Следовательно,
Осталось доказать, что
По теореме Фалеса и
— середины диагоналей. Следовательно,
(
— общий,
как соответственные при
и секущей
). Следовательно,
(
— общий,
как соответственные
при
и секущей
). Следовательно,
Так как — средняя линия трапеции
то
Следовательно, то есть
значит,
—
трапеция. Чтд.
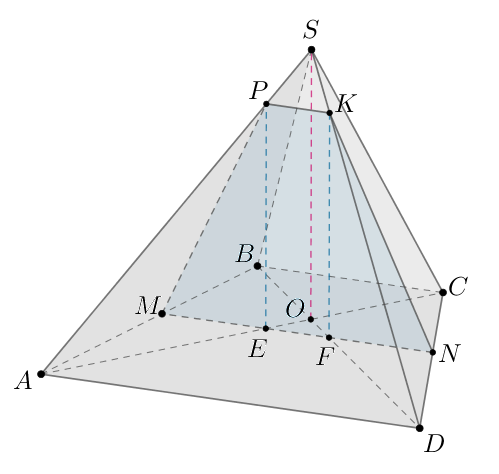
б) По свойству трапеции
Тогда
Так как
то
Из описанного в пункте а), следует, что
Из описанного в пункте а), следует, что
Также средняя линия равна
Так как
— высота трапеции
Следовательно, ее площадь равна
б) 24
Ошибка.
Попробуйте повторить позже
В прямой пятиугольной призме высота
равна
а четырехугольльник
— прямоугольник со сторонами
а) Докажите, что плоскости и
перпендикулярны.
б) Найдите объем многогранника
Источник:
а) Сечение призмы плоскостью — четырехугольник
Построим
сечение призмы плоскостью
Назовем эту плоскостью плоскостью
Найдем линию пересечения
и плоскости
Плоскости
и
параллельны, следовательно, плоскость
пересечет их
по параллелльным прямым. Значит, если
то проведем
Получается, что
— точка пересечения прямой
с
плоскостью
а значит и плоскости
с плоскостью
Так
как
то
пересечет плоскость
по прямой
(см.рис.). Следовательно,
— сечение призмы плоскостью
Докажем, что Тогда по признаку получим, что
по ТТП
Докажем, что то есть докажем, что
План такой:
1) найдем
и
2) найдем
3) найдем
4)
докажем, что
Отсюда будет следовать, что
- 1.
- Проведем
Так как
равнобедренный, то
— середина
Следовательно, по теореме Пифагора
Так как
то
Следовательно,
По теореме Пифагора
- 2.
- 3.
Следовательно, можно принять
Тогда
- 4.
-
Таким образом, и
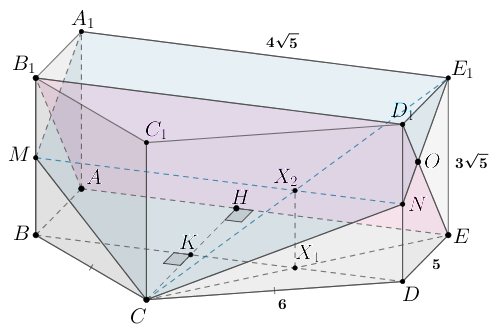
б) — параллелограмм, следовательно,
Следовательно,
— середина
Следовательно,
— медиана и
высота в
Тогда
Объем многогранника равен (
— объем всей призмы)
- 1.
- Найдем
- 2.
- Найдем
Следовательно,
- 3.
- Найдем
- 4.
- Найдем
Следовательно,
б) 180
Ошибка.
Попробуйте повторить позже
В правильную треугольную пирамиду с боковым ребром и стороной
основания
вписан шар. Плоскость
перпендикулярна высоте пирамиды и
проходит через ее середину.
а) Докажите, что плоскость и шар пересекаются более чем в одной
точке.
б) Найдите площадь сечения шара плоскостью
Источник:
а) Пусть — правильная треугольная пирамида с основанием
По
свойству правильной пирамиды центр
вписанного в нее шара лежит на ее
высоте
Пусть
— высота основания,
— середина высоты
Плоскость пересекает шар в более чем одной точке, если расстояние от центра
шара до плоскости меньше радиуса шара. Так как то
следовательно, требуется доказать, что
Это равносильно тому, что
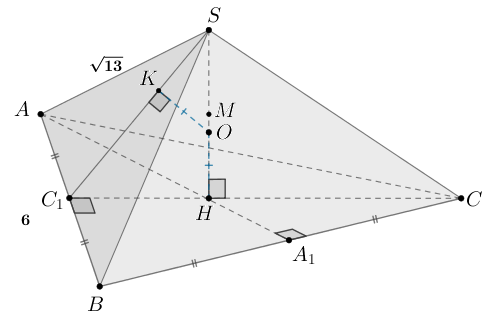
Высота правильного треугольника со стороной равна
следовательно,
Тогда по теореме Пифагора
Так как
то по теореме Пифагора
Рассмотрим
— радиусы шара. Так как
то
Так как то
Чтд.
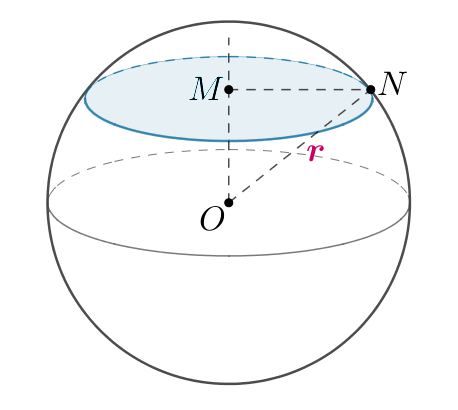
б) Сечение шара плоскостью — окружность с центром в точке
радиуса
Рассмотрим прямоугольный
Следовательно, площадь сечения равна
б)
Ошибка.
Попробуйте повторить позже
Сторона основания правильной четырехугольной пирамиды относится
к боковому ребру как
Через вершину
проведена плоскость
перпендикулярная боковому ребру
и пересекающая его в точке
а) Докажите, что — середина
б) Найдите расстояние между прямыми и
если высота пирамиды
равна
Источник:
а) Пусть тогда
Так как
— квадрат, то
следовательно,
— правильный. Значит, в этом треугольнике высота
является также и медианой, то есть
— середина
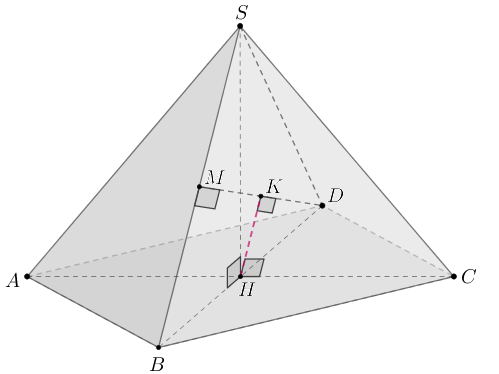
б) — высота пирамиды,
— точка пересечения диагоналей основания.
Следовательно,
Так как
то
Проведем
Тогда
следовательно, по определению
—
расстояние между
и
Так как — середина
то по теореме Фалеса
—
середина
Следовательно,
— средняя линия
и
Высота правильного треугольника со стороной равна
следовательно,
б) 3
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Сторона основания правильной четырехугольной пирамиды относится
к боковому ребру как
Через вершину
проведена плоскость
перпендикулярная боковому ребру
и пересекающая его в точке
а) Докажите, что сечение пирамиды плоскостью
— это
четырехугольник, диагонали которого перпендикулярны.
б) Найдите площадь этого сечения, если боковое ребро пирамиды равно
Источник:
а) Пусть — высота пирамиды
Так как эта пирамида правильная,
то
— точка пересечения диагоналей квадрата
Так как то
перпендикулярна любой прямой из
Следовательно,
Пусть
Так как
то по теореме о трех перпендикулярах
Проведем через точку
прямую
(см. рис.). Тогда
Следовательно,
— сечение пирамиды плоскостью
Также
по теореме о трех перпендикулярах
Следовательно, так как
то диагонали сечения
и
перпендикулярны. Что и
требовалось доказать.
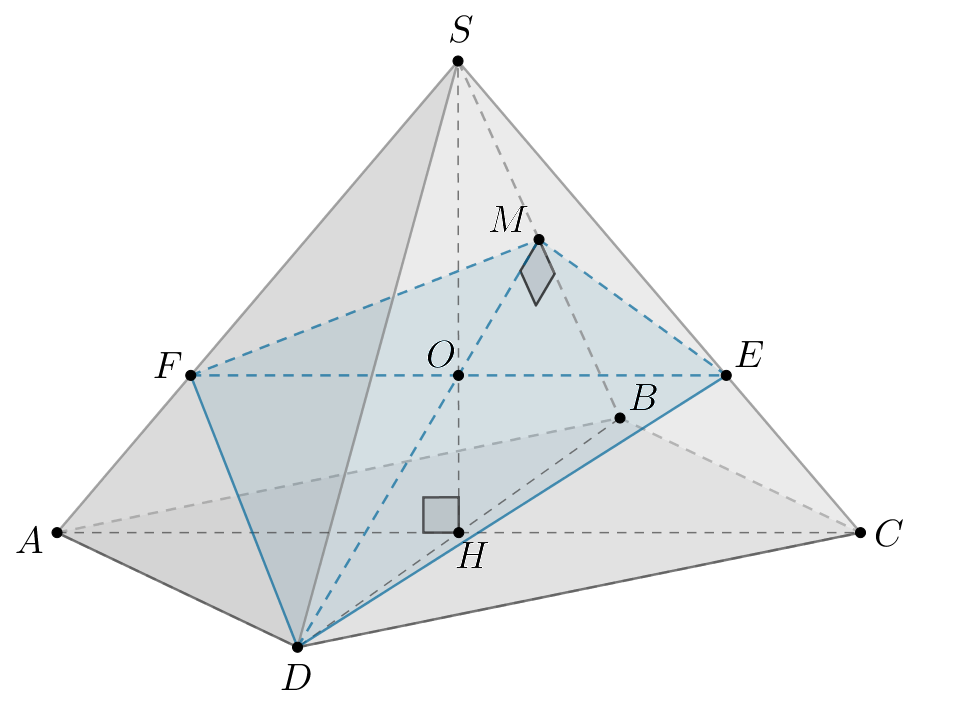
б) Так как диагонали сечения взаимно перпендикулярны, то площадь
сечения можно искать по формуле
По условию а
Следовательно,
Следовательно,
Значит,
равносторонний. Тогда
Так как равносторонний, то
и
— не только высоты, но и
медианы этого треугольника. Следовательно, точкой пересечения они делятся в
отношении
считая от вершины. Тогда
следовательно,
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Грань куба
является вписанной в основание
конуса, а сечением конуса плоскостью
является круг, вписанный в
четырехугольник
а) Высота конуса равна ребро куба равно
Докажите, что
б) Найдите угол между плоскостями и
где
— вершина
конуса.
Источник:
а) Радиус основания конуса равен половине диагонали квадрата то есть
равен
Радиус окружности, вписанной в
равен половине
стороны этого квадрата, то есть
следовательно,
Так как то
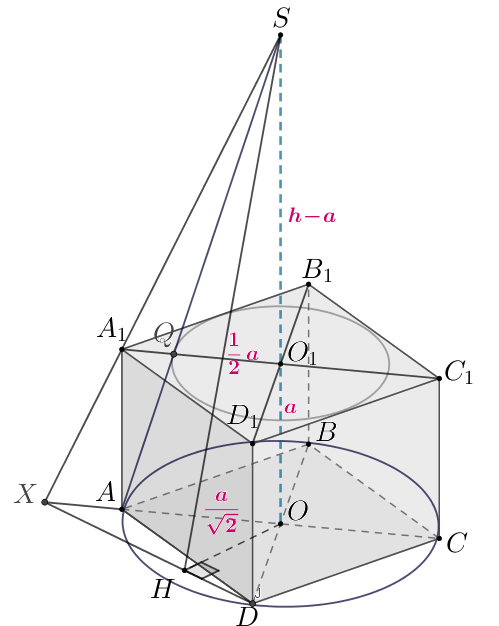
б) Найдем линию пересечения плоскости с плоскостью
Для
этого найдем точку пересечения прямой
с плоскостью
— это точка
Тогда
— искомая линия пересечения.
пусть Тогда по ТТП
Следовательно,
—
угол между
и
.
Из по теореме Пифагора
По свойству высоты, опущенной из вершины прямого угла треугольника, получаем
Тогда из
б)
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна
высота
равна
Точка
— середина бокового ребра
Плоскость,
параллельная плоскости
проходит через точку
и пересекает ребра
и
в точках
и
соответственно.
а) Докажите, что площадь четырехугольника составляет
площади
треугольника
б) Найдите объем пирамиды
Источник:
а) Параллельные плоскости пересекают любую плоскость по параллельным
прямым. Следовательно, так как то
Следовательно, так как
— середина
то по теореме Фалеса
и
—
середины
и
сооветственно. Тогда
по двум сторонам и
углу между ними. Следовательно,
Что и требовалось доказать
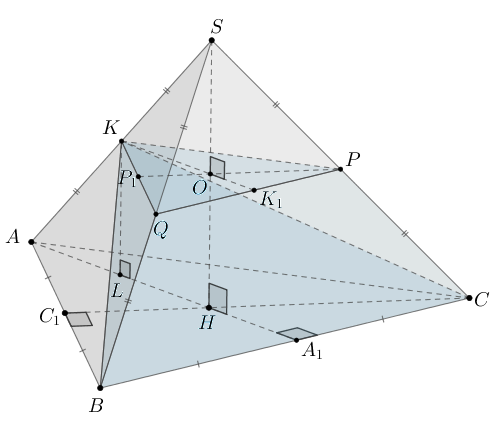
б) Пусть
Тогда
- 1.
- Найдем
Так как все стороны
в 2 раза меньше сторон
то эти треугольники подобны, следовательно,
Обозначим
Пирамида
— правильная, так как ее боковые ребра равны
боковых ребер пирамиды
а
— равносторонний. Следовательно, основание высоты
этой пирамиды — точка
— центр
Так как
то
следовательно,
лежит на высоте
(
— общий, оба треугольника прямоугольные). Следовательно,
Тогда
- 2.
- Найдем
Провели
По теореме Фалеса
— середина
следовательно,
— средняя линия в
и
Тогда
- 3.
- Найдем
Так как
— правильный, то
следовательно,
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме на ребрах
и
отмечены
точки
и
соответственно так, что
а) Докажите, что плоскость проходит через середину ребра
б) Найдите площадь сечения призмы плоскостью
если
Источник:
а) Пусть
Пусть также
и
— проекции
точек
и
на плоскость
Так как
то плоскость
пересечет эти плоскости по параллельным прямым. Следовательно,
Тогда
следовательно,
Значит, — середина
Чтд.
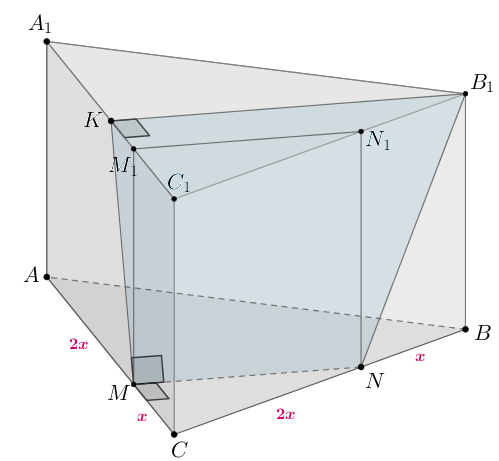
б) Из условия следует, что
Тогда
Тогда по теореме Пифагора
Заметим, что так как то
— трапеция (из пункта а)
также следует, что
). Так как
и
то
Так как
то
— высота трапеции
— высота правильного
следовательно,
Из следует, что
Тогда площадь сечения равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной призме с основанием
боковое ребро
равно
а сторона основания равна
Через точку
перпендикулярно
плоскости
проведена прямая
а) Докажите, что прямая пересекает отрезок
и делит его в отношении
б) Найдите угол между прямыми и
Источник:
а) Пусть — точка пересечения диагоналей основания
Так как
и
то
Проведем
Тогда
следовательно,
Пусть прямая
пересекает луч
в точке
причем
Так как и
то точка
лежит между точками
и
то есть на отрезке
причем
Чтд.
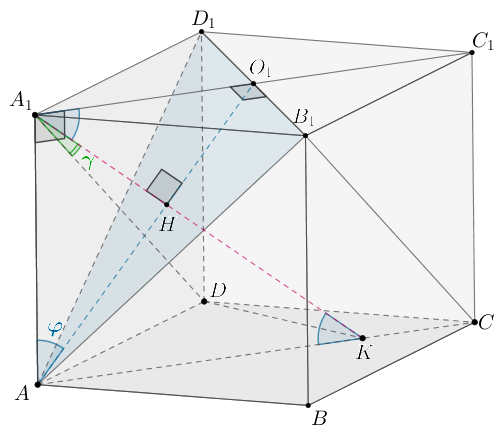
б) Так как то
По теореме косинусов из
По теореме Пифагора
Следовательно, по теореме косинусов из
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основание пирамиды — прямоугольный треугольник
с
прямым углом при вершине
Высота пирамиды проходит через точку
а) Докажите, что середина ребра равноудалена от вершин
и
б) Найдите угол между плоскостью и прямой, проходящей через
середины ребер
и
если известно, что
Источник:
а) Так как то
Так как
то
по теореме о трех перпендикулярах
Следовательно,
Пусть — середина
Требуется доказать, что
Но
и
— медианы в прямоугольных треугольниках
и
проведенные
к общей гипотенузе, следовательно, они равны половине гипотенузы, то
есть
Что и требовалось доказать.
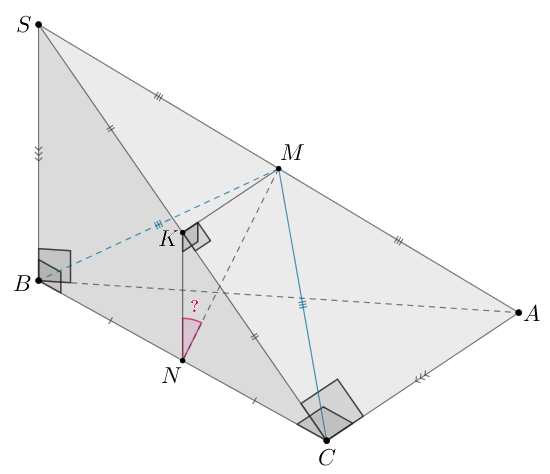
б) Пусть — середина
Так как
то
Проведем
Тогда
Следовательно,
— проекция
на плоскость
Следовательно, требуется найти
Так как — середина
и
то
— средняя линия с
треугольнике
то есть
— середина
Следовательно,
Так как и
— середины
и
соответственно, то
— средняя
линия треугольника
то есть
По условию значит,
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте а) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме точка
— середина ребра
а
Плоскость
проходит через точки
и
параллельно
прямой
а) Докажите, что плоскость делит ребро
в отношении
б) Найдите расстояние от точки до плоскости
если
Источник:
а) Если то
содержит прямую, параллельную
Отложим на
продолжении отрезка
за точку
отрезок
Тогда
следовательно,
— параллелограмм,
следовательно,
Тогда плоскость
— это плоскость
Пусть Докажем, что
Пусть
—
середина
Тогда
и
Тогда
следовательно,
Чтд.

б) Рассмотрим треугольную пирамиду Пусть
— длина
перпендикуляра от точки
до плоскости
Тогда, с одной стороны, это
пирамида с вершиной в точке
и с основанием
а с другой стороны, это
пирамида с вершиной в точке
и с основанием
Следовательно, ее
объем равен
Так как то
По теореме Пифагора
По теореме косинусов из
Пусть Тогда по теореме косинусов из
Следовательно,
Следовательно,
Тогда
б)
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме точки
и
— середина ребер
и
соответственно. Плоскость
проходит через точки
и
параллельно прямой
а) Докажите, что сечением призмы плоскостью
является
равнобедренная трапеция.
б) Найдите угол между прямой и плоскостью
если
Источник:
а) Пусть Тогда
— точка пересечения плоскости
и
плоскости грани
Проведем через
прямую
Она
пересечет
в точке
Тогда
— сечение призмы плоскостью
как пряямоугольные по катету
и острому углу
(вертикальные). Следовательно,
Тогда, так как по построению
— параллелограмм,
— середина
Следовательно,
как прямоугольные по катету
и острому углу
(вертикальные). Следовательно,
— середина
Тогда
— средняя линия в
значит,
Таким образом,
Заметим также, что
то есть
следовательно,
— трапеция.
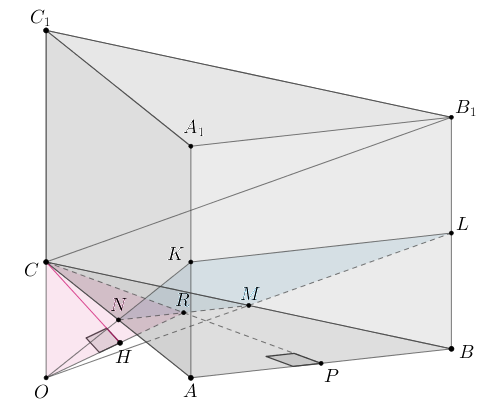
б) Так как и равны половине стороны основания, то
Пусть
— середина
Так как
равнобедренный, то
Следовательно,
Если мы проведем
то
Следовательно,
— проекция прямой
на
плоскость
Следовательно, требуется найти
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В правильной шестиугольной пирамиде сторона основания
равна
а боковое ребро
равно
Точка
— середина ребра
Плоскость
перпендикулярна плоскости
и содержит точки
и
Прямая
пересекает плоскость
в точке
а) Докажите, что
б) Найдите объем пирамиды
Источник:
а) Пусть — высота пирамиды. Пусть
Восстановим из точки
перпендикуляр к плоскости
то есть проведем
Тогда
. Таким образом, из одной точки
проведены две плоскости
и
перпендикулярные плоскости
. Следовательно, эти
плоскости совпадают, то есть совпадают точки
и
. Таким образом,
то есть
Так как по свойству правильного шестиугольника то по
теореме Фалеса
— середина
Следовательно,
— медиана и
высота
следовательно, он равнобедренный, то есть
Чтд.
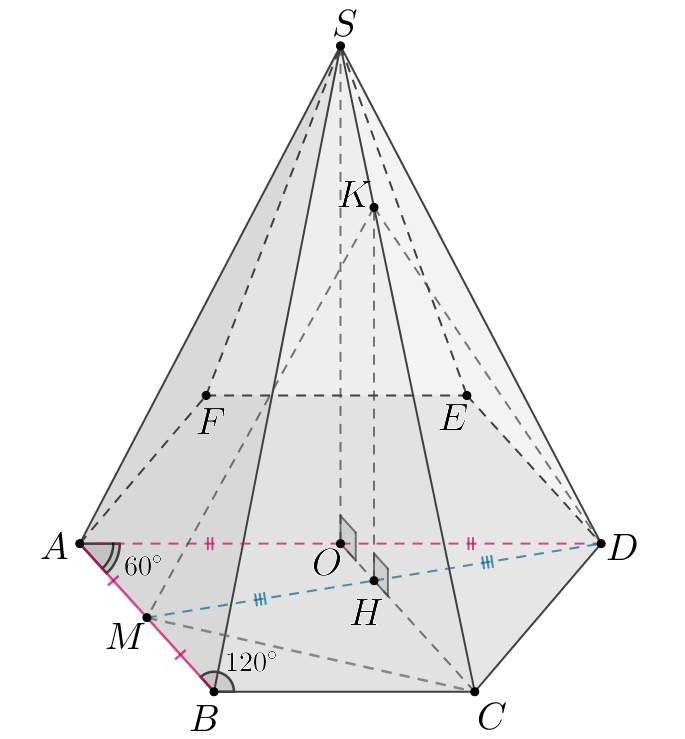
б) — высота пирамиды
— ее основание. Так
как
— средняя линия
то
как прямоугольные с общим углом
следовательно,
Трапеция отрезками
и
разбивается на 3 правильных
треугольника со стороной равной
следовательно,
следовательно,
следовательно,
Следовательно,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании четырехугольной пирамиды лежит прямоугольник
со сторонами
Длины боковых ребер пирамиды
а) Докажите, что — высота пирамиды.
б) Найдите угол между прямыми и
Источник:
а) Так как — верно, то по обратной теореме
Пифагора
Аналогично по обратной теореме Пифагора, так как имеем
Следовательно,
перпендикулярна двум пересекающимся прямыми
из плоскости
следовательно,
Следовательно,
— высота
пирамиды.
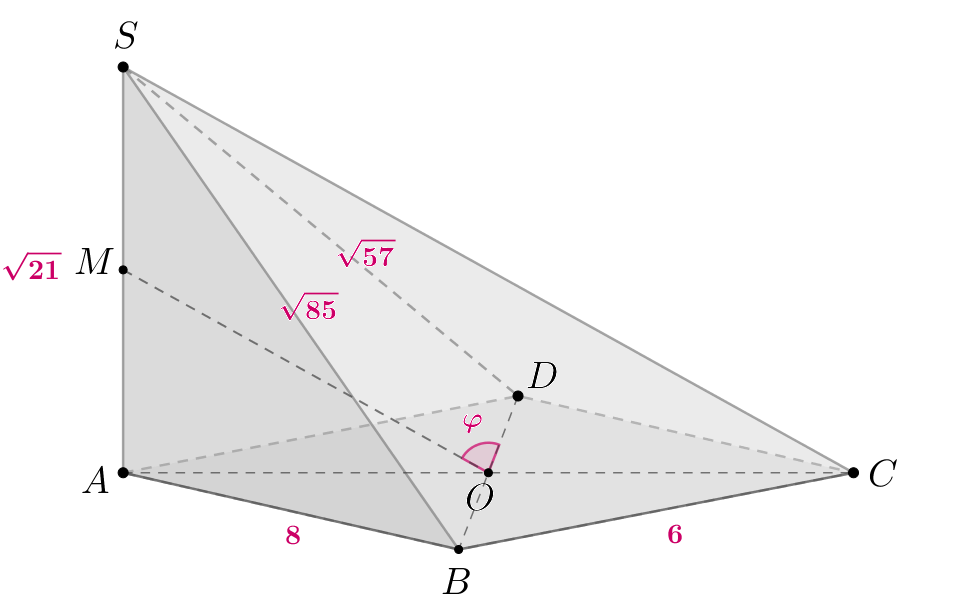
б) Пусть — точка пересечения диагоналей
Тогда
— середина
Проведем
Тогда
— угол между прямыми
и
Найдем его по теореме косинусов из
Для этого найдем стороны
этого треугольника.
По теореме Фалеса — середина
Тогда
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде сторона основания
равна
а
боковое ребро
равно
На ребрах
и
отмечены точки
и
соответственно, причем
а) докажите, что плоскость перпендикулярна плоскости
б) Найдите объем пирамиды
Источник:
а) Проведем Пусть
пересекает
в точке
Тогда
—
линия пересечения плоскостей
и
Проведем
— высоту
пирамиды
Докажем, что
тогда из
будет
следовать, что
откуда будет следовать, что
По теореме Менелая для и прямой
Следовательно, Так как
то
Так как то по обратной теореме Фалеса
Чтд.
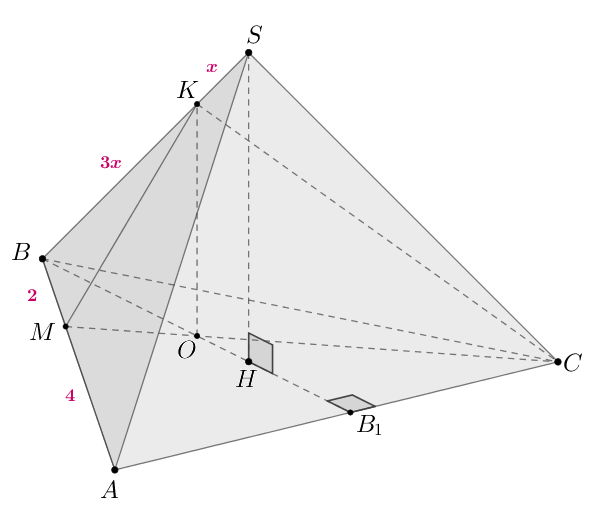
б) Объем пирамиды равен
Из пункта а) следует, что Высота правильного треугольника
равна
Тогда
Так как площади треугольников, имеющих общую высоту, относятся как основания, то
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде сторона основания
равна
а боковое ребро
равно
На ребрах
и
отмечены точки
и
соответственно, причем
Плоскость
перпендикулярна плоскоссти
и содержит точки
и
а) Докажите, что плоскость содержит точку
б) Найдите площадь сечения пирамиды плоскостью
Источник:
а) Проведем в плоскости прямую
где
— высота пирамиды
(см.рис.). Тогда плоскость
содержит точку
так как
По
теореме Фалеса
то есть
Тогда
Так как и
то
Следовательно,
Следовательно, точки
и
лежат на
одной прямой, то есть плоскость
содержит точку
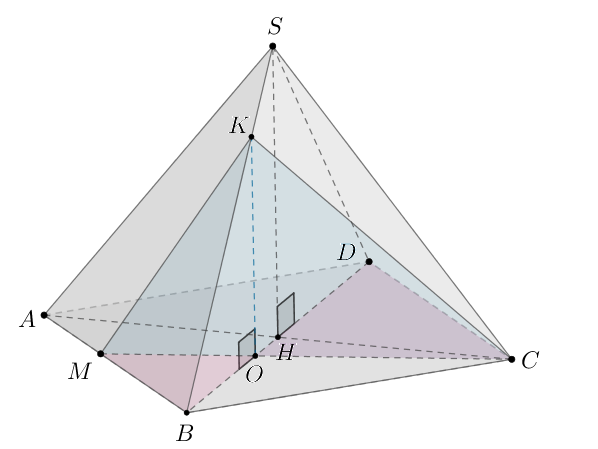
б) Так как то
следовательно, пощадь сечения
пирамиды плоскостью
равна
По теореме Пифагора
По теореме Пифагора
Из следует, что
Следовательно,
б)



