Ошибка.
Попробуйте повторить позже
Дана треугольная призма Точка
— середина ребра
Плоскость
проходит через ребро
и
перпендикулярна прямой
а) Докажите, что одна из диагоналей грани равна одной из ее сторон.
б) Найдите расстояние от точки до плоскости
если
делит ребро
в отношении
считая от точки
и
Источник:
а) По условию Если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой, лежащей в этой
плоскости, в частности,
Так как — призма, то
следовательно,
Рассмотрим треугольник в одноименной плоскости. Отрезок
является его медианой и высотой, значит,
— равнобедренный, то есть
Таким образом, в грани
диагональ
равна стороне
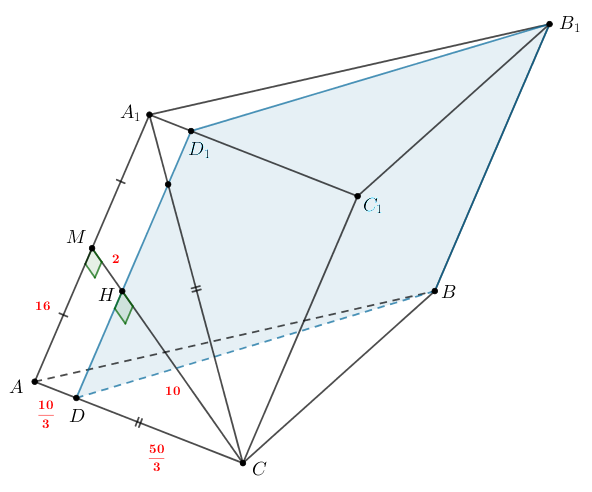
б) Пусть плоскость пересекает прямую
в точке
прямую
— в точке
, прямую
— в точке
Заметим, что все эти три точки лежат в грани
Значит, они лежат на прямой пересечения грани
плоскостью
Нам нужно найти расстояние от точки до плоскости
то есть длину
так как
а
— точка пересечения
и
По условию имеем:
Отсюда получаем
По условию значит,
Тогда

Рассмотрим треугольники и
Они подобны, так как
— общий и
как
соответственные углы, образованные параллельными прямыми
и
и секущей
Тогда имеем:
Найдем По условию
— середина
значит,
Треугольник — прямоугольный, тогда по теореме Пифагора:
Таким образом,
Отсюда Теперь можем найти длину
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании пирамиды с вершиной лежит прямоугольник
со
сторонами
и
Все боковые рёбра пирамиды равны
На
рёбрах
и
отмечены точки
и
соответственно так, что
Плоскость сечения проходит через точки
и
перпендикулярно ребру
а) Докажите, что плоскость сечения пересекает ребро в его середине.
б) Найдите расстояние от точки до плоскости сечения.
а)
1. Проведём диагональ и отрезок
которые пересекаются в точке
2. Рассмотрим и
как накрест лежащие,
как накрест
лежащие и
откуда
и
равны по двум углам и
стороне.
3. У равных треугольников равные соответствующие элементы, следовательно,
Это в свою очередь означает, что точка
— точка пересечения
диагоналей прямоугольника в основании, то есть принадлежит плоскости
сечения.
4. Рассмотрим прямоугольный По теореме Пифагора:
откуда
5. Рассмотрим По обратной теореме Пифагора:
откуда получаем, что
—
прямоугольный.
6. Провед̈eм Тогда
— средняя линия по определению, откуда
— середина ребра
7. поскольку
Следовательно, точка
также
принадлежит плоскоскости сечения, ведь эта плоскость перпендикулярна ребру
Ч.Т.Д.
![]()
Для профилактики доведём построение сечения до конца.
1. Продлим прямую до точки пересечения с прямой
— точки
Проведём отрезок
пересекающий
в точке
Проведём
2. Поскольку — прямоугольник, то длины противоположных сторон
равны, откуда
3. Рассмотрим и
и
— один и тот же угол, откуда
4. Из выявленного подобия выводим отношения отрезков:
5. Запишем теорему Менелая для и секущей
Теперь мы знаем положение всех вершин сечения и его построение полностью завершено.
б)
1.
Факт: расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на эту плоскость.
2. Заметим, что раз и
плоскости сечения, то
плоскости
сечения. То есть расстояния от каждой точки данной прямой до этой
плоскости одинаковы.
3. Таким образом, мы можем найти расстояние от точки до плоскости
сечения и автоматически найти ответ.
4. Поскольку ребро плоскости сечения, то
— перпендикуляр,
опущенный из точки
на плоскость сечения (то есть его длина равна искомому
расстоянию). Длина
равна половине длины ребра
(
— середина
),
то есть
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Все ребра призмы равны между собой. Углы
и
равны
каждый. Найдите расстояние от точки
до плоскости
, если
площадь грани
равна
Пусть ребро призмы равно Тогда
Заметим, что , следовательно, если
,
— середина,
то
, следовательно, из
следует, что
.
Получаем, что
и
— квадрат. Тогда
, следовательно, в
стороны равны
, значит, по обратной теореме Пифагора он
прямоугольный и
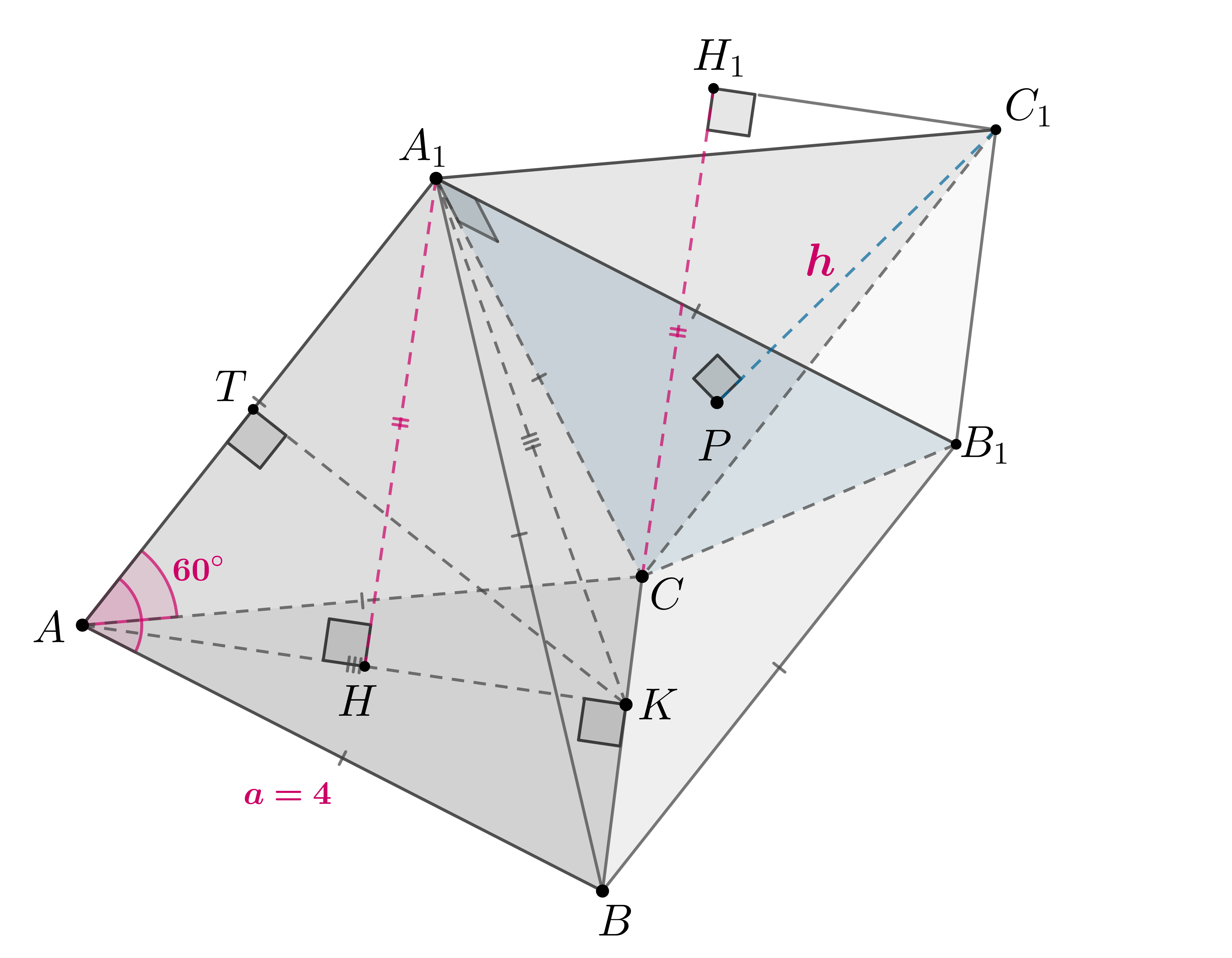
Пусть . Тогда
(как расстояние между двумя
параллельными плоскостями, содержащими основания призмы). Пусть
,
,
,
,
. Тогда по методу
объемов
- 1.
- Найдем
:
- 2.
- Найдем
.
. Проведем
,
— середина
, тогда по теореме Пиифагора
Тогда
- 3.
- Найдем
. Так как
прямоугольный и равнобедренный с катетами
, то
Следовательно,
Ошибка.
Попробуйте повторить позже
Основание наклонной призмы
— квадрат, а все
боковые грани призмы — равные ромбы. Углы
и
равны
каждый. Найдите расстояние от точки
до плоскости
, если сторона
квадрата
равна 10.
и
— равнобедреннные с углом
, следовательно, они
равносторонние, значит,
— точка пересечения
диагоналей квадрата, следовательно,
— медиана и высота в равнобедренном
, значит,
. Также
, следовательно,
— прямоугольник со сторонами
,
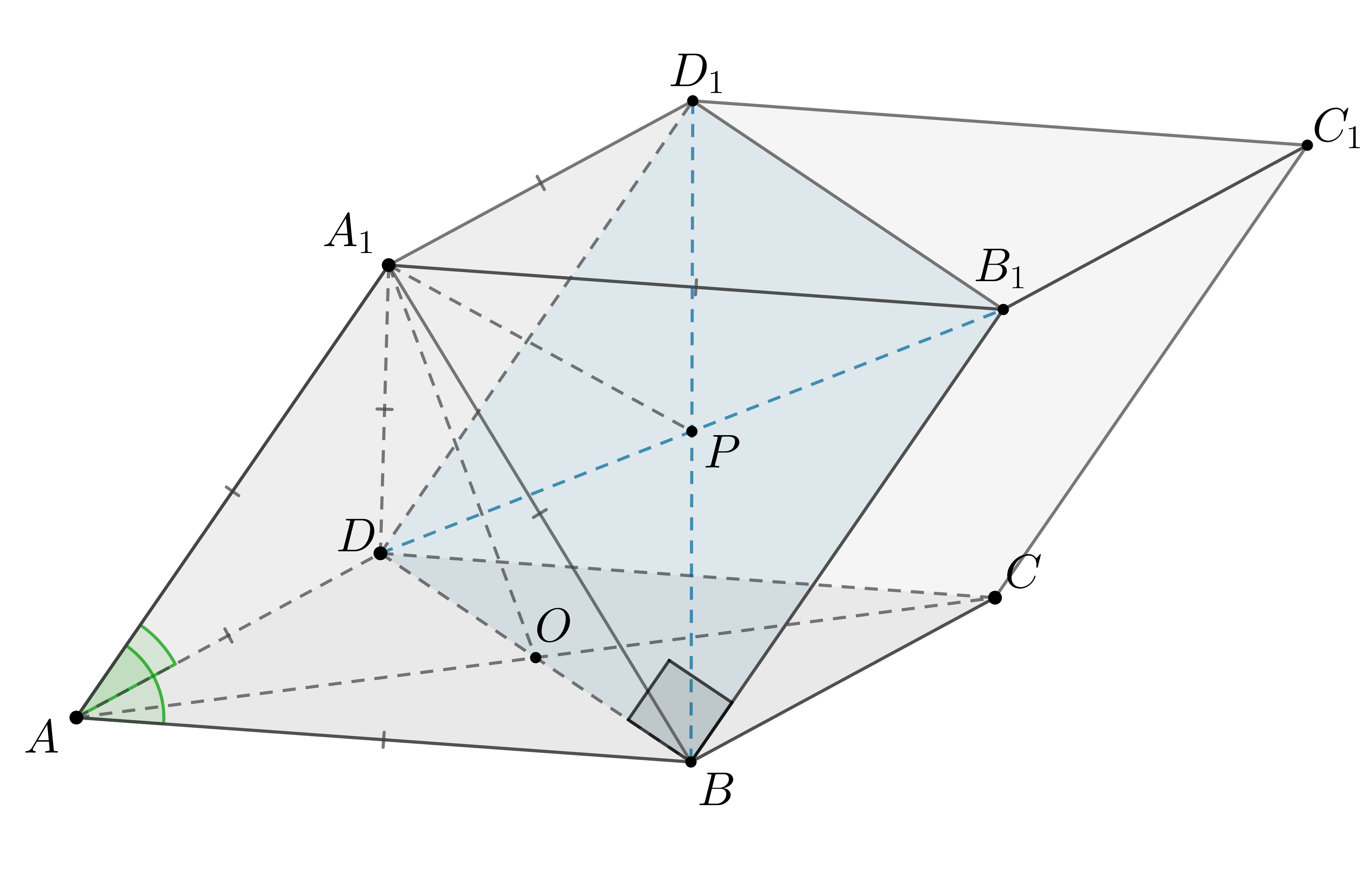
Пусть . Так как боковые ребра пирамиды
равны,
то
— центр описанной около
окружности, следовательно,
—
точка пересечения диагоналей этого прямоугольника.
Ошибка.
Попробуйте повторить позже
Расстояния от концов отрезка до некоторой плоскости равны 1 и 3. Чему может быть равно расстояние от середины этого отрезка до той же плоскости?
Существует два возможных варианта взаиного расположения отрезка относительно плоскости: он целиком находится по одну сторону от нее или он ее пересекает. Оба варианта изображены на рисунке. Рассмотрим каждый из них.
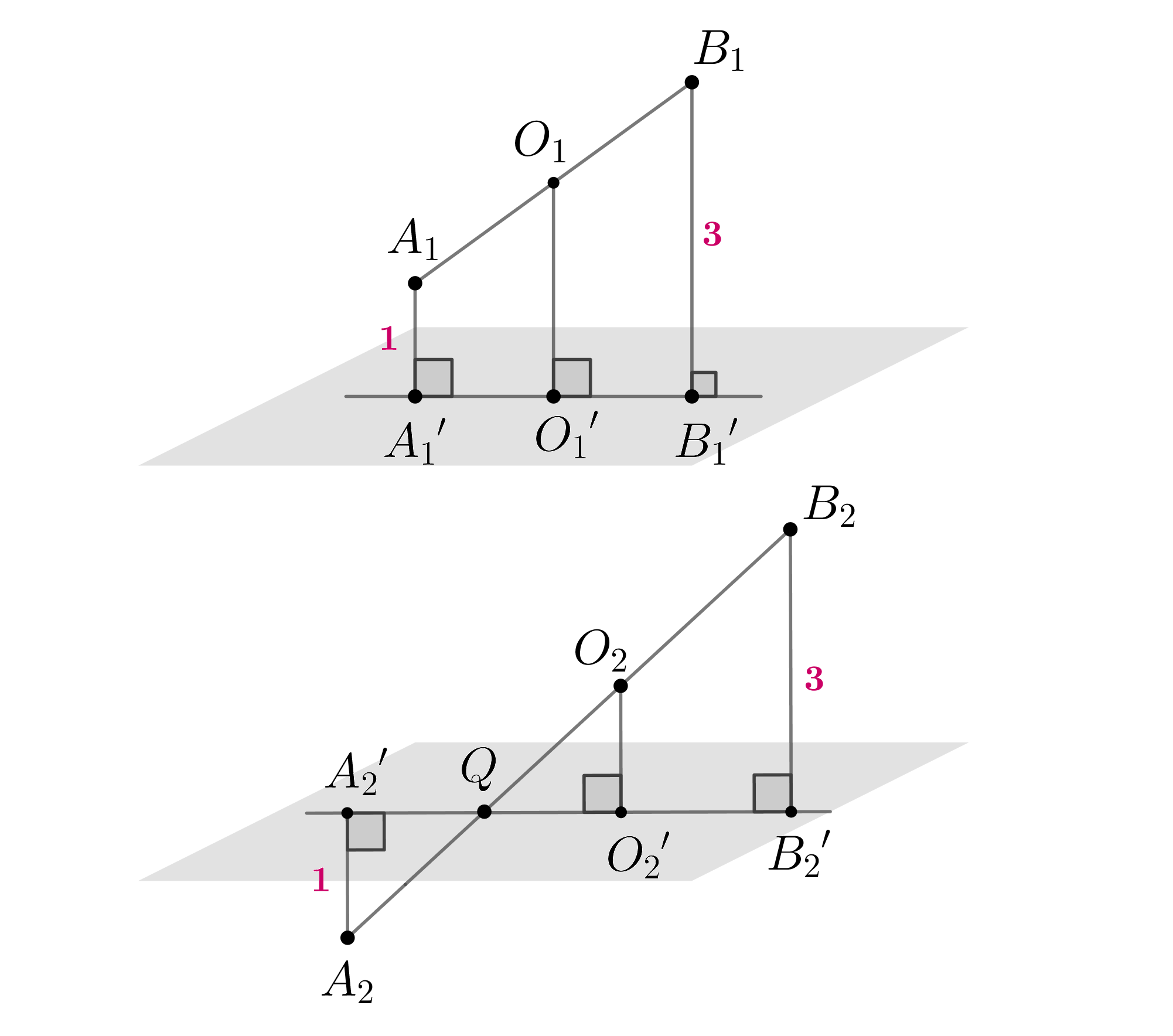
- 1.
— отрезок,
— его середина,
— проекции точек
на плоскость. Заметим, что
, следовательно, все точки лежат в одной плоскости, следовательно, точки
лежат на одной прямой.
Получили трапецию
, в которой
— средняя линия. Следовательно, она равна полусумме оснований, значит.
- 2.
— отрезок,
— точка пересечения отрезка и плоскости,
— его середина,
— проекции точек
на плоскость. Заметим, что
, следовательно, все точки лежат в одной плоскости, следовательно, точки
лежат на одной прямой.
как прямоугольные по острому углу, следовательно,
. Пусть
,
. Следовательно,
, откуда
2 или 1
Ошибка.
Попробуйте повторить позже
На каком расстоянии от ребра правильной пирамиды
с вершиной
должна проходить плоскость
, параллельная ребрам
и
, чтобы
площадь сечения пирамиды этой плоскостью была максимальной?
Пусть
— высота пирамиды, следовательно, так как пирамида
правильная,
— точка пересечения медиан
.
Так как и
, то
Так как
и
, то
. Аналогично для
:
,
:
,
:
;
. Следовательно,
параллелограмм
— сечение пирамиды плоскостью
. Так как
в правильной треугольной пирамиде ребро основания перпендикулярно
противоположному ему боковому ребру, то
(
— наклонная, а
— ее проекция, следовательно, по ТТП из
следует
). Так
как
то
, следовательно,
—
прямоугольник. Пусть
. Проведем
. Аналогично
доказательству в скобках
— наклонная,
— ее проекция, следовательно,
из
следует
. Так как также
, то
—
искомое расстояние.
Пусть ,
,
. Тогда
.
, следовательно,
, следовательно,
Следовательно,
принимает максимальное значение тогда, когда принимает максимальное
значение функция
.
Следовательно,
, значит,
, причем достигается это значение при
. Значит,
— середина
Тогда
Ошибка.
Попробуйте повторить позже
На ребре правильной пирамиды
объемом
взята такая точка
,
что
Расстояние от центра основания
до плоскости
равно
Найдите площадь треугольника
Пусть
Пусть
— центр правильного
, то есть
точка пересечения его медиан (высот), тогда
(которая перпендикулярна
) — наклонная,
— ее проекция, следовательно, из
по ТТП
следует
. Следовательно,
перпендикулярна двум пересекающимся
прямым
и
плоскости
, следовательно,
Проведем ,
. Тогда (пусть
)
так как как прямоугольные по острому углу
Заметим, что мы доказали попутно факт:
Плоскость, проходящая через ребро тетраэдра, делит противоположное ему ребро в том же отношении, в котором она делит объем тетраэдра.
Тогда
Заметим, что какп прямоугольные по общему острому
углу
, следовательно,
Значит,
Ошибка.
Попробуйте повторить позже
Плоскость , параллельная боковому ребру
и ребру
основания
правильной пирамиды
, проходит на расстоянии
от
ребра
. Найдите площадь сечения пирамиды этой плоскостью.
Пусть
— высота пирамиды, следовательно, так как пирамида
правильная,
— точка пересечения медиан
. Следовательно,
Так как и
, то
Так
как
и
, то
. Аналогично для
:
,
:
. Следовательно, параллелограмм
— сечение пирамиды плоскостью
. Так как в правильной
треугольной пирамиде ребро основания перпендикулярно противоположному ему
боковому ребру, то
(
— наклонная, а
— ее проекция,
следовательно, по ТТП из
следует
). Так как
то
, следовательно,
— прямоугольник. Пусть
. Проведем
. Аналогично доказательству в скобках
— наклонная,
— ее проекция, следовательно, из
следует
. Так как также
, то
, следовательно,
Так как и
Так как и
Тогда площадь сечения равна
Ошибка.
Попробуйте повторить позже
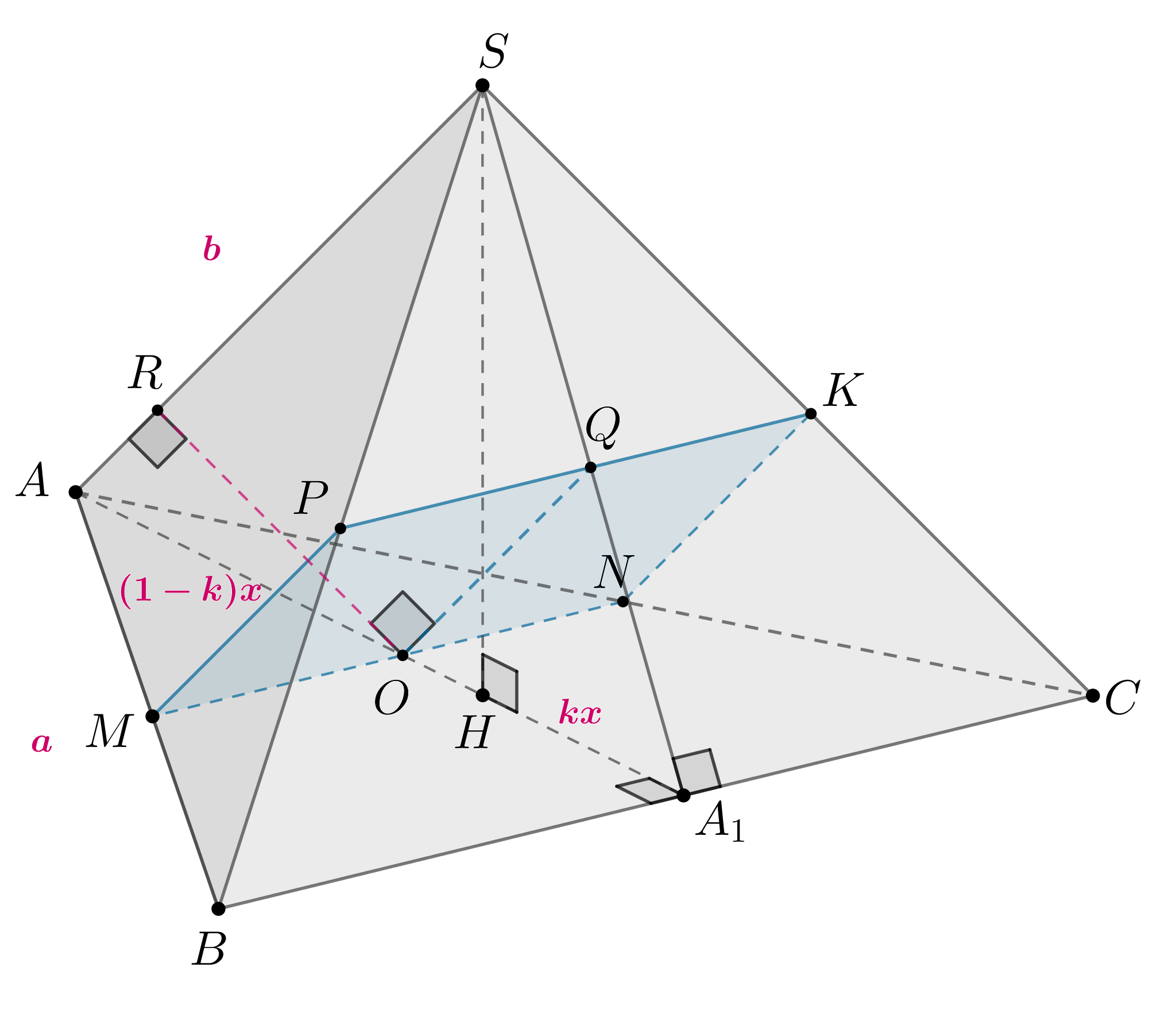
На ребрах и
куба
с ребром
отмечены точки
и
соответственно, причем
,
. Плоскость
пересекает ребро
в точке
.
а) Докажите, что – середина
.
б) Найдите расстояние от до плоскости
.
а) Чтобы построить точку , достаточно продлить прямую
до пересечения с
в точке
, а затем пересечь
с ребром
куба.
с коэффициентом
.
с коэффициентом
.
б) Опустим перпендикуляр на
, проведем отрезок
. По теореме о трех перпендикулярах, из
следует
. Опустим перпендикуляр
на
.
лежит в плоскости
. Таким образом,
перпендикулярен двум непараллельным прямым (
и
) плоскости
, а значит, и самой плоскости. Осталось найти длину
.
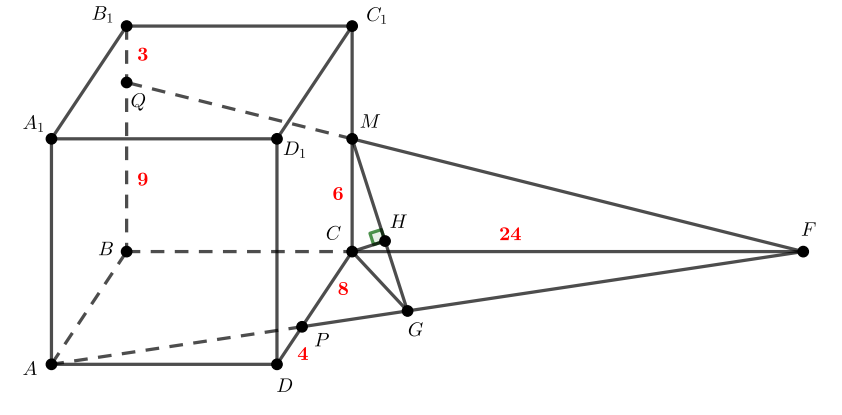
— прямоугольный, тогда его высота
— прямоугольный, тогда его высота
б)
Ошибка.
Попробуйте повторить позже
В основании четырехугольной пирамиды лежит равнобедренная трапеция
, причем
,
. Угол между прямыми
и
равен
. Известно, что
–
высота пирамиды.
Найдите расстояние от точки до грани
.
Так как – основания трапеции, то
параллельна плоскости
, в которой находится
прямая
. Следовательно, расстояние от любой точки прямой
до плоскости
будет
одинаковым. Найдем расстояние до плоскости
от точки
.
Так как – высота пирамиды, то
. Проведем
(точка
упадет на
продолжение отрезка
за точку
).
Если – точка пересечения прямых
и
, то
. Так как также
(так как трапеция равнобедренная), то
равносторонний и
.
Следовательно, и
.
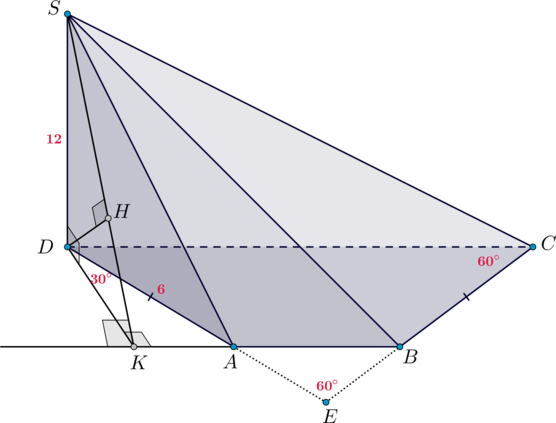
По теореме о трех перпендикулярах (заметим, что
). Тогда перпендикуляр
из точки
на плоскость
упадет на
(в противном случае по теореме о трех
перпендикулярах проекция
наклонной
будет перпендикулярна
и тогда
будут существовать в одной плоскости два перпендикуляра
и
к прямой
, что
невозможно).
Таким образом, необходимо найти .
Из прямоугольного треугольника
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида причем грани
и
представляют собой равные равнобедренные треугольники с
прямыми углами при вершине
Найдите расстояние от точки
до грани
если высота пирамиды равна
и равна
Из условия задачи следует, что:
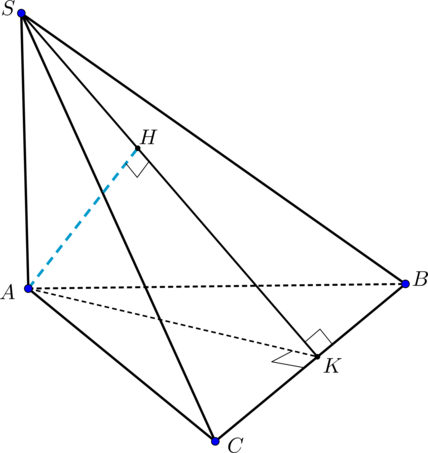
Так как — равнобедренный, то
— середина
. Аналогично,
.
Таким образом, перпендикуляр на плоскость
упадет на прямую
, поскольку в таком случае выполнена
теорема о трех перпендикулярах:
— проекция,
— наклонная, обе перпендикулярны
. Тогда
— искомое
расстояние.
По теореме Пифагора в :
Тогда
По теореме Пифагора в :
Ошибка.
Попробуйте повторить позже
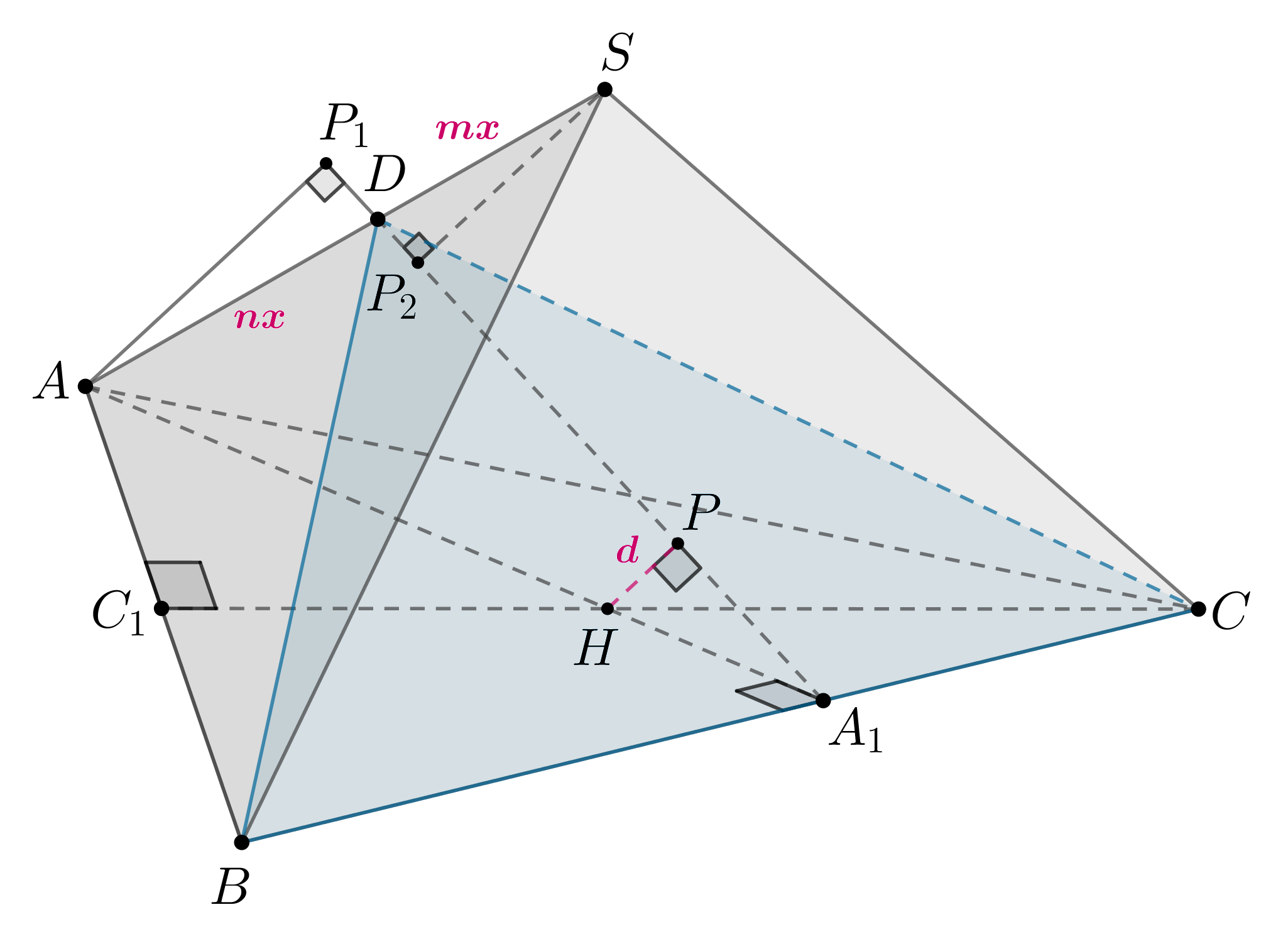
– правильный тетраэдр с ребром
.
– такие точки на ребрах
соответственно, что
. Плоскость
пересекает ребро
в точке
. Найдите расстояние от точки
до плоскости
.
1) По условию представляет собой правильную треугольную пирамиду, все ребра которой
равны
. Найдем, в каком отношении точка
делит отрезок
. Для этого построим сечение
пирамиды плоскостью
. Продлим прямую
до пересечения с прямой
– получим точку
. Соединив точки
и
, получим линию пересечения основания – отрезок
(сечением
является четырехугольник
).
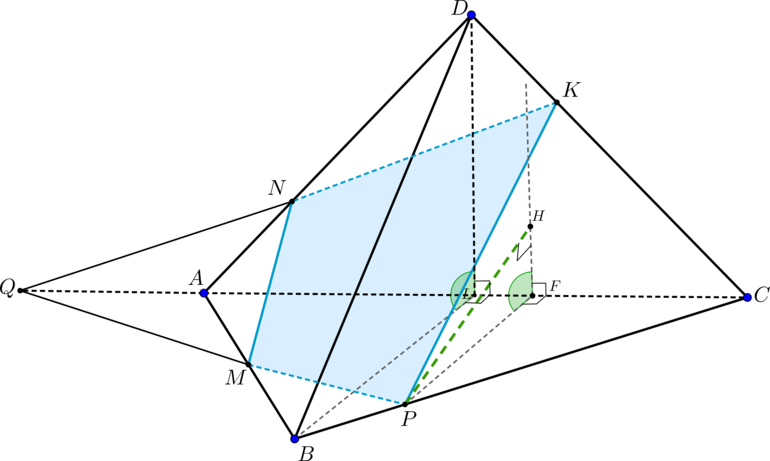
По теореме Менелая для и прямой
имеем:
.
Аналогично для и прямой
:
.
2) Проведем и
. Тогда по теореме о трех перпендикулярах
,
следовательно,
. Найдем
из треугольника
. Для этого найдем
и
.
Проведем , тогда
. Треугольник
– равнобедренный
(
). По теореме косинусов найдем
Тогда .
Таким образом, .
.
Ошибка.
Попробуйте повторить позже
Дана правильная четырехугольная пирамида с вершиной
Через точку пересечения диагоналей основания провели
плоскость
перпендикулярно ребру
Найдите расстояние от точки
до плоскости
если
— середина
а
высота пирамиды равна 11.
Построим сечение пирамиды плоскостью Так как
то
перпендикулярна двум пересекающимся прямым, лежащим
в
Обозначим
Проведем
По теореме о трех перпендикулярах как наклонная, поскольку
— проекция.
Таким образом, имеем две пересекающиеся прямые и
в плоскости
Значит, сечением пирамиды плоскостью
является треугольник
Проведем следовательно,
Так как расстояния от любой точки прямой, параллельной плоскости, до этой
плоскости одинаковы, то имеем:
Здесь буквой обозначили расстояние.
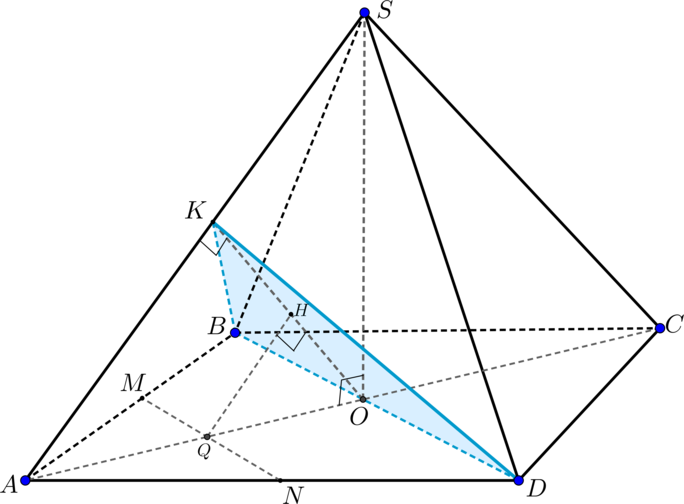
Так как по условию то проведем
следовательно,
По построению — средняя линия
следовательно,
Тогда
— средняя линия
и
В имеем:
Тогда из подобия треугольников и
Тогда искомое расстояние равно
Ошибка.
Попробуйте повторить позже
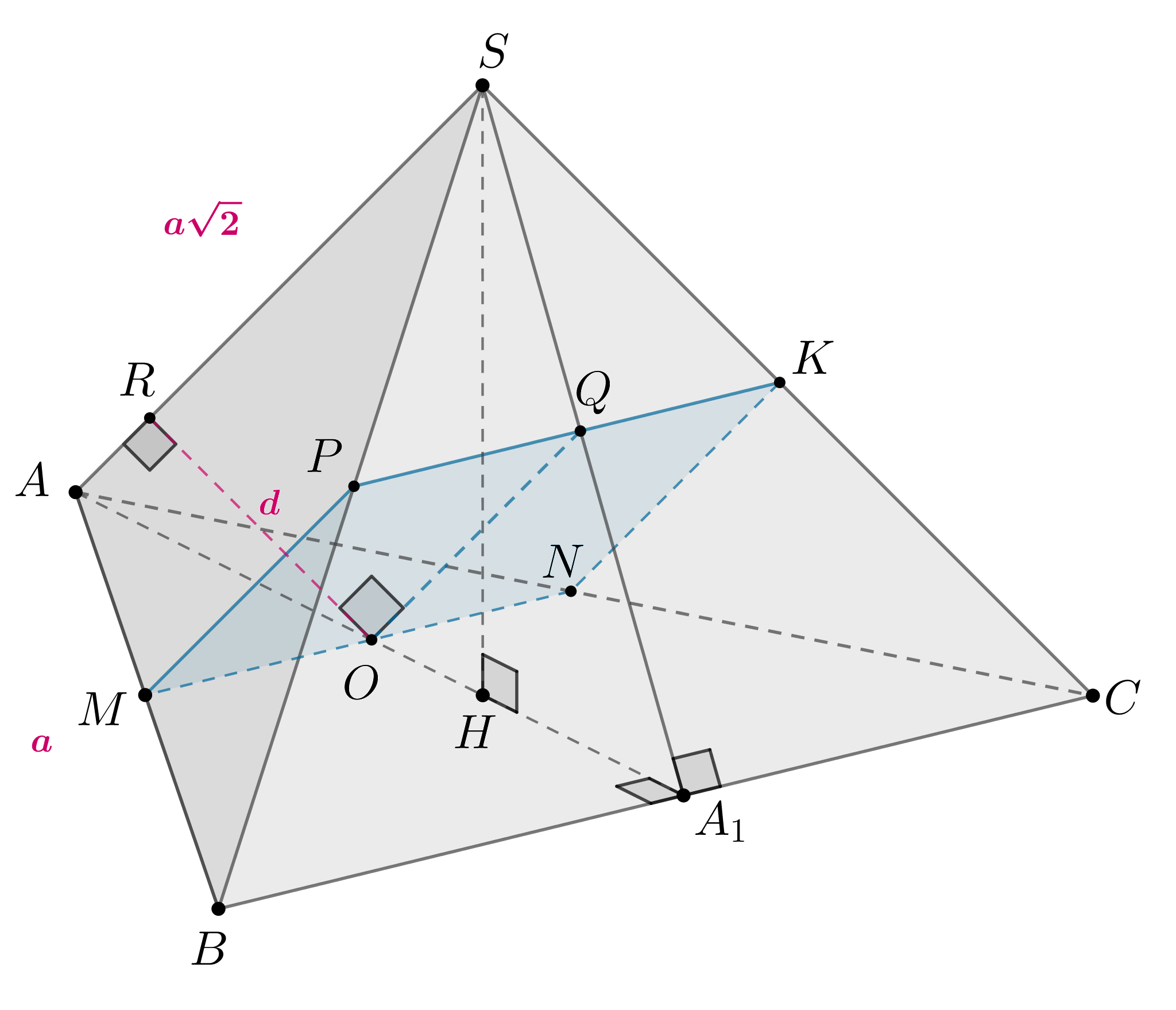
На ребрах и
куба
с ребром 12 отмечены точки
и
соответственно, причем
Плоскость
пересекает ребро
в точке
а) Докажите, что точка является серединой ребра
б) Найдите расстояние от точки до плоскости
а) Обозначим за плоскость
Продлим прямую
до пересечения с прямой
в точке
Точка
лежит в
плоскости
а также в плоскости
Тогда и
лежит в плоскости
значит, точка пересечения
и
и есть точка
Так как то
по двум углам с коэффициентом подобия, равным
Тогда
Так как то
по двум углам с коэффициентом подобия, равным
Тогда имеем:
Получили, что — середина
что и требовалось.
![]()
б)
Способ 1.
Пусть — объем пирамиды
— искомое расстояние от точки
до плоскости
Заметим, что
совпадает
с высотой из точки
на плоскость
Тогда можем записать
двумя способами:
По теоремам Пифагора для треугольников
![]()
По теореме косинусов для угла треугольника
Способ 2.
![]()
Произведем дополнительное построение. Пусть — основание высоты из
в треугольнике
а
основание высоты
из
в треугольнике
Докажем, что
перпендикулярно плоскости
По теореме о трех перпендикулярах так как
Тогда
и
перпендикулярна плоскости
Тогда
так как лежит в
при этом
по построению.
Получили, что
перпендикулярна прямым
и
из плоскости
а значит перпендикулярна всей плоскости.
Осталось найти длину
чтобы решить задачу.
Треугольник — прямоугольный, тогда его высота равна
Аналогично для треугольника
б)
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде точка
– середина
, точка
– середина
.
Через точки
и
параллельно
проведена плоскость
.
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки до плоскости
, если известно, что
,
.
а) Построим сечение пирамиды плоскостью . Т.к. точки
и
являются серединами сторон, то
– средняя линия, следовательно,
.
Т.к. плоскость параллельна прямой
, то она пересечет грани
и
по прямым,
параллельным
. Следовательно,
.
Т.к. ,
,
, то
, причем
.
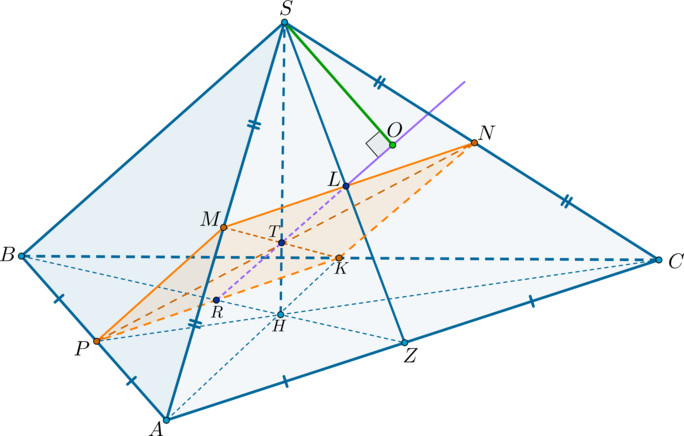
Таким образом, имеем: ,
, следовательно,
– параллелограмм. Т.к.
и
– середина стороны
, то по теореме Фалеса
– середина ребра
. Аналогично
– середина ребра
. Т.к. пирамида правильная, то ее боковые ребра равны, следовательно,
.
Рассмотрим и
: они равны по двум сторонам и углу между ними (
, т.к.
в основании лежит правильный треугольник; боковые ребра наклонены к плоскости основания под
одинаковым углом, т.к. пирамида правильная).
Таким образом, . То есть диагонали параллелограмма
равны, следовательно,
по признаку он является прямоугольником.
б) Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из этой точки на
плоскость. Т.к. , то
. Также очевидно, что
.
Пусть – перпендикуляр на плоскость
(то есть точка
). Тогда по теореме о трех
перпендикулярах (
,
– наклонная) проекция
(заметим, что
).
Таким образом, мы имеем в плоскости
две прямые
и
, которые перпендикулярны прямой
, что возможно только если они параллельны. Но они не параллельны, т.к. имеют одну общую
точку
, значит, эти прямые совпадают, то есть точка
должна лежать на прямой
.
Следовательно, перпендикуляр
из точки
на плоскость
будет падать на продолжение отрезка
.
Рассмотрим плоскость :
, следовательно,
Найдем ,
,
.
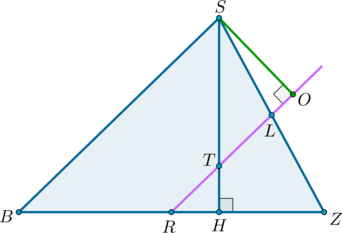
Т.к. – правильный, то
(как высота).
Т.к. – средняя линия,то
.
Т.к. и
еще и медианы, а медианы точкой пересечения делятся в отношении
, считая
от вершины, то
. Таким образом,
.
Т.к. плоскость , то
. Тогда
с коэффициентом
. Таким
образом,
.
По той же причине .
Т.к. – прямоугольный, то
, следовательно,
.
Тогда из равенства имеем:
б)



