Нахождение площади сечения —Каталог задач по ЕГЭ - Математика

Тема 14. Задачи по стереометрии

14.12 Нахождение площади сечения

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи по стереометрии

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#46502

В правильной треугольной призме $ABCA1B1C1$ сторона основания $AB = 6,$ а боковое ребро $AA1 = 5.$ На ребре $CC1$ взята точка $K$ так, что $CK :KC1 = 1:4,$ а на ребре $A1C1$ взята точка $M$ так, что $A1M :MC1 = 1:2.$

а) Докажите, что плоскость $BKM$ делит ребро $A1B1$ в отношении $2:5,$ считая от точки $A1.$

б) Найдите площадь сечения призмы плокостью $BKM.$

Показать ответ и решение

а) Пусть прямая $MK$ пересекает прямую $AA1$ в точке $O.$ Тогда это точка пересечения плоскости $BMK$ с плоскостью $AA1B1.$ Следовательно, плоскость $BMK$ пересекает плоскость $AA1B1$ по прямой $BO.$ Следовательно, $N = BO ∩ A1B1.$

Из условия следует, что $A1M = 2,$ $MC1 = 4,$ $CK = 1,$ $KC1 = 4.$ Так как $△KC1M ∼ △OA1M$ как прямоугольные по острому углу ( $∠KMC1 =∠OMA1$ как вертикальные), то $OA = 2. 1$

Также $△OA1N ∼ △OAB$ как прямоугольные по общему острому глу $O,$ следовательно,

OA1- A1N- 12 12- 30 OA = AB ⇒ A1N = 7 ⇒ NB1 = 6− 7 = 7 ⇒ A1N :NB1 = 12:30= 2:5.

$PIC$

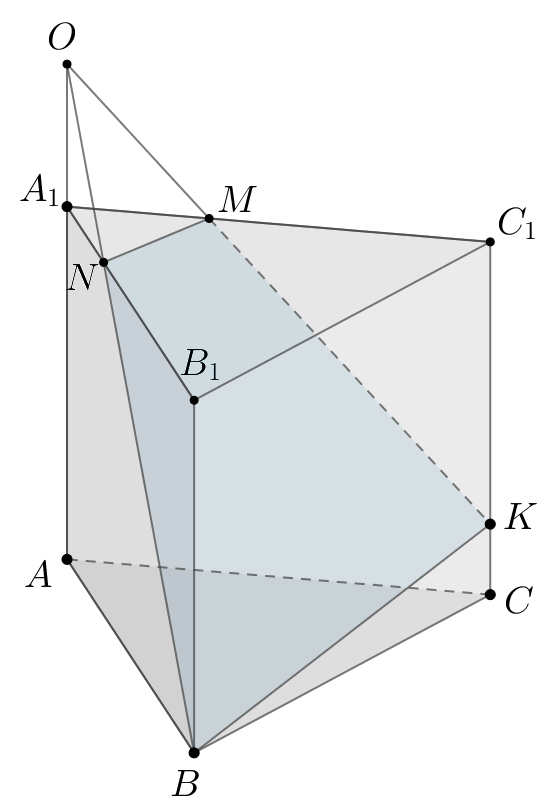
б) $SBKMN = SBKO − SNMO.$ Найдем нужные значения:

∘ ------ √-- BK = 62+ 12 = 37; √- MK = 4 2; √ - MO =2 2; KO = 6√2; ∘ ------ √-- OB = 62+ 72 = 85; √-- ON = 2OB = 2 85. 7 7

По теореме косинусов из $△BKO :$

2 2 2 ∘ --- ∘ --- cos∠BOK = BO--+-KO--−-BK--= 10 ⇒ sin∠BOK = 7-. 2⋅BO ⋅KO 17 17

Следовательно,

1 19√ -- SBKMN = 2 sin∠BOK ⋅(BO ⋅KO − NO ⋅MO )= -7 70.

Ответ:

б) $√ -- 19-70 7$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#22061

Дан куб $ABCDA1B1C1D1$ с ребром, равным $a$ . На ребрах $AB$ и $AD$ основания $ABCD$ взяты точки $M$ и $N$ соответственно так, что $AM : M B = 2 : 1$ и $AN : N D = 2 : 1$ . Найдите площадь сечения куба плоскостью, проходящей через точки $M, N, C 1$ .

Показать ответ и решение

Обозначим $γ$ — плоскость сечения. Независимо от того, в каких точках $γ$ пересекает ребра $BB1$ и $DD1$ куба, проекцией сечения на плоскость $(ABCD )$ будет пятиугольник $DCBM N$ . Найдем его площадь, а также угол между плоскостью сечения и плоскостью $(ABCD )$ , чтобы найти площадь самого сечения.

$PIC$

$AM : M B = AN : N D = 2 : 1 ⇒ M N ∥ BD$ ; $CA ⊥ DB ⇒ CP ⊥ M N$ . По теореме от трех перпендикулярах $C1P$ также перпендикулярен $M N$ , значит, угол $α$ между $P C1$ и $PC$ равен углу между плоскостью сечения и плоскостью $(ABCD )$ .

1 a√-- )} √ - CO = OA = 2CA = 2 ⇒ CP = CO + OP = 4√a--= 2--2a- M P ∥ BO ⇒ OP : PA = BM : M A = 1 : 2 ⇒ OP = 13 ⋅√a-=-a√-) 3 2 3 2 3 2

Тогда в прямоугольном треугольнике $CP C1$

- - PC PC 2√2a 2√-2a 2√2 cosα = ----= ∘----2-----2-= ∘---3-----= -√317-= √--- PC1 P C + CC 1 89a2 + a2 3 a 17

Пусть $S$ — площадь сечения, $Sp$ — площадь его проекции на $(ABCD )$ , тогда

( ) √ -- √ -- Sp SABCD − SANM a2 − 12 ⋅ 23a 2 79a2 7 17 2 7 34 2 S = cosα-= -----cosα----- = -----2√√2----- = 2√√2-= 18√2-a = --36-a 17 17

Ответ:

$7a2√34 ------- 36$

Ошибка.
Попробуйте повторить позже

Задача 3#19806

Дана правильная шестиугольная призма $ABCDEF A1B1C1D1E1F1.$ Плоскость $α$ проходит через через точки $B,$ $C1$ и $D1.$

а) Докажите, что сечение призмы плоскостью $α$ является трапецией.

б) Найдите площадь сечения, если известно, что $AB = BB1 = 10.$

Показать ответ и решение

а) Обозначим через $α$ плоскость сечения. Плоскости $(B1C1D1 )$ и $(BCD )$ параллельны, следовательно, плоскость $α$ сечет их по параллельным прямым. Плоскость $α$ пересекает $B1C1D1$ по прямой $D1C1.$ Докажем, что прямая $EB$ параллельна $D1C1,$ из этого будет следовать, что она лежит в $α,$ так как $B ∈ α$ .

Прямые $EB ∥ DC$ в силу правильности шестиугольника $ABCDEF,$ так как в нем $∘ ∠BED = 60,$ $∘ ∠EDC = 120 ,$ следовательно, сумма односторонних углов равна $180∘.$ Прямые $DC ∥D C , 1 1$ следовательно, $EB ∥ D C . 1 1$ Тогда $E$ лежит в $α$ и $ED1C1B$ — искомое сечение. Кроме того, в четырехугольнике $ED1C1B$ противолежащие стороны $EB$ и $D1C1$ параллельны и не равны, следовательно, $ED1C1B$ — трапеция.

$PIC$

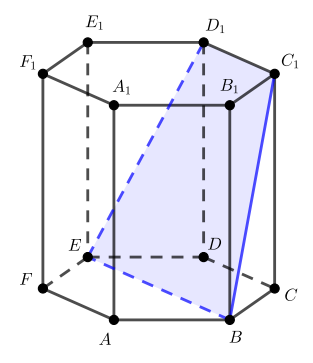
б) Способ 1.

В правильном шестиугольнике $EB = 2DC = 2AB = 20,$ также по условию $D1C1 = AB = 10.$ По теореме Пифагора для треугольника $BCC1 :$

BC = ∘BC2-+-CC2-= √100-+100-=10√2-= ED 1 1 1

Найдем полупериметр трапеции:

√ - √- p= 2⋅10-2+-10+-20= 15+ 10 2 2

Равнобокую трапецию можно вписать в окружность, тогда по формуле Брахмагупты ее площадь равна

S = ∘ (p−-ED1)(p−-D1C1)(p-− BC1-)(p-− EB-)=

∘ -2-------√---------√--- √- = 15 ⋅(5+ 10 2)(−5+ 10 2)= 75 7

Способ 2.

Введём векторный базис из векторов $−A→F =−→a,$ $−B−→C = −→b ,$ $−−C→C1 = −→c.$ Длины этих векторов $a =b = c= 10.$ Из определения правильной призмы $−→a ⊥ −→c$ и $−→ −→ b ⊥ c ,$ а поскольку шестиугольник $ABCDEF$ — правильный, то прямые $AF$ и $BC$ образуют угол $∘ 60.$ Тогда можно посчитать скалярное произведение:

(−→a,−→b )= a⋅b⋅cos60∘ = 10⋅10⋅0,5 = 50 −→ −→ ∘ (a, c)= a⋅c⋅cos90 = 0 (−→b ,−→c)= b⋅c⋅cos90∘ = 0

$PIC$

В пункте а) было ранее доказано, что $EBC1D1$ — трапеция. По свойствам правильного шестиугольника диагональ $BE = 2a.$ Тогда для определения площади сечения можно сначала посчитать площадь треугольника $EBC1,$ после чего домножить её на $1,5,$ поскольку площадь $EC1D1$ составляет половину от площади $EBC1.$ Выразим векторы $BE$ и $BC1$ через базисные вектора и найдём квадраты длин:

−−→ −→ BE =2AF =2−→a −−→ −−→ −−→ −→ −→ BC1 = BC + CC1 = b + c BE2 = (2a)2 = 4a2 = 202 2 −→ −→ 2 −→ −→ 2 −→ −→ 2 −→ −→ 2 2 2 2 BC 1 = ( b + c ) = (b ,b )+ (c ,c) − 2(b ,c )= b +c = 2a = 2 ⋅10

Таким образом,

1 1 ∘------------- SEBC1 = 2BE ⋅BC1 sin ∠EBC1 = 2BEBC1 1 − cos2∠EBC1 = ∘ --------------------------- ∘------------------- = 1 BE2BC21 − BE2BC21 cos2∠EBC1 = 1 BE2BC21 − (−B−→E, −B−C→1)2 = 2 ∘ ----------------- ∘ ---2------------------ = 1 8a4− (2−→a,−→b + −→c )2 = 1 8a4 − 4(−→a ,−→b )2− 4(−→a,−→c)2 = 2 ∘ ---------------2-- = 1 2⋅2002− 4⋅502− 2⋅0= 1 ⋅100√8-−-1= 50√7 2 2

Тогда площадь трапеции равна

√- SEBC1D1 = 1,5SEBC1 = 75 7

Ответ:

б) $√ - 75 7$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 4#11263

Правильная треугольная пирамида рассечена плоскостью, перпендикулярной основанию и делящей две стороны основания пополам. Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна $2$ , а высота пирамиды равна $4$ .

Показать ответ и решение

Отметим середины сторон треугольника основания и его центр $O$ . Пусть $H$ — точка пересечения $AO$ и $EF$ . Восстановим в точке $H$ перпендикуляр к плоскости основания. Этот перпендикуляр обязательно пересечет отрезок $AD$ в некоторой точке $K$ , т.к. $AO$ является ортогональной проекцией $AD$ . Тогда $K$ и есть точка сечения принадлежащая ребру $AD$ . Найдем площадь $EKF$ .

$PIC$

$HK$ и $OD$ параллельны как перпендикуляры к плоскости основания, тогда $△ AKH ∼ △ADO$ и

$KH-- DO$ = $AH-- AO$ ⇒ KH = $AH-⋅DO-- AO$

$AH = 1AG 2$ , т.к. $EF$ — средняя линия. $AO = 2AG 3$ , т.к. $O$ — центр треугольника. Тогда $AH : AO = 3 : 4$ . Учитывая, что $OD = 4$ , получаем

KH = $AH--⋅DO-- AO$ = $3 4$ DO = 3

EF = $1 2$ BC = 1 ⇒ S_EFK = $1 2$ EF ⋅ KH = $3 2$

Ответ:

$1,5$

Ошибка.
Попробуйте повторить позже

Задача 5#2675

$SABCD$ – четырехугольная пирамида, в основании которой лежит квадрат $ABCD$ , а две боковые грани $SAB$ и $SAD$ представляют собой прямоугольные треугольники с прямым углом $∠A$ .

1) Проведите плоскость $α$ через точку пересечения диагоналей основания параллельно грани $SBC$ .

2) Найдите площадь сечения пирамиды плоскостью $α$ , если $SA = AB = a$ .

Показать ответ и решение

1) Пусть $AC ∩ BD = O$ . Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

$PIC$

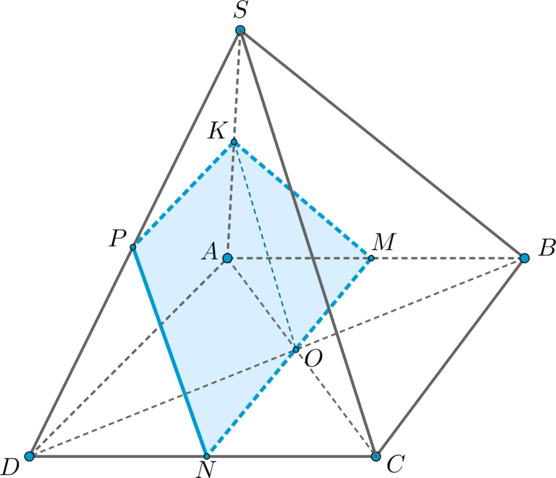
Заметим, что т.к. $∠SAB = ∠SAD = 90 ∘ ⇒ SA ⊥ (ABC )$ .

Проведем в плоскости $SAC$ прямую $OK ∥ SC$ . Т.к. $O$ – середина $AC$ , то по теореме Фалеса $K$ – середина $SA$ . Через точку $K$ в плоскости $SAB$ проведем $KM ∥ SB$ (следовательно, $M$ – середина $AB$ ). Таким образом, плоскость, проходящая через прямые $OK$ и $KM$ , и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки $O$ и $M$ , получим прямую $M N$ .

Т.к. $α ∥ (SBC )$ ,то $α$ пересечет плоскость $SCD$ по прямой $N P ∥ SC$ (если $N P ∩ SC ⁄= ∅$ , то $α ∩ (SBC ) ⁄= ∅$ , что невозможно ввиду их параллельности).

Таким образом, $KM N P$ – искомое сечение, причем $KP ∥ AD ∥ M N ⇒$ это трапеция.

2) Т.к. все точки $K, M, N, P$ – середины отрезков $SA, AB, CD, SD$ соответственно, то:

а) $M N = AD = a$

б) $KP = 1-AD = a- 2 2$

в) $√ -- KM = 1SB = a--2- 2 2$

Заметим, что по теореме о трех перпендикулярах $SB ⊥ BC ⇒ KM ⊥ M N$ . Таким образом, $KM N P$ – прямоугольная трапеция.

$√ -- KP---+-M-N-- 3--2-2 SKMNP = 2 ⋅ KM = 8 a$

Ответ:

1) Рисунок.

2) $√ -- 3 2 2 ----a 8$

Ошибка.
Попробуйте повторить позже

Задача 6#2659

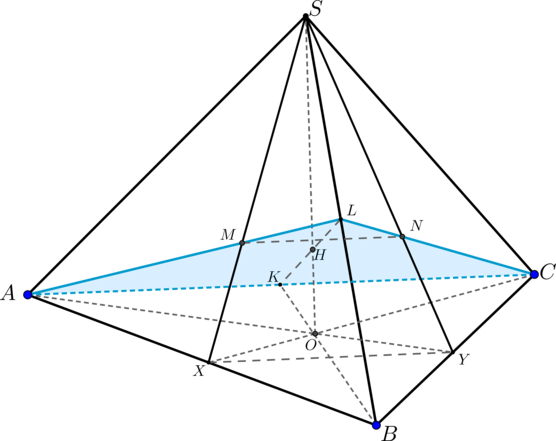
$ABCD$ – правильный тетраэдр с ребром $24$ . $M, N, K$ – такие точки на ребрах $AB, AD, CD$ соответственно, что $DN = 2N A = CK = BM$ .

а) Постройте сечение пирамиды плоскостью $M N K$ .

б) Найдите площадь сечения тетрадра плоскостью $M N K$ .

Показать ответ и решение

а) По условию $ABCD$ представляет собой правильную треугольную пирамиду, все ребра которой равны $24$ . Построим сечение пирамиды плоскостью $M N K$ . Продлим прямую $N K$ до пересечения с прямой $AC$ – получим точку $Q$ . Соединив точки $Q$ и $M$ , получим линию пересечения основания – отрезок $M T$ . Таким образом, сечением является четырехугольник $M N KT$ .

$PIC$

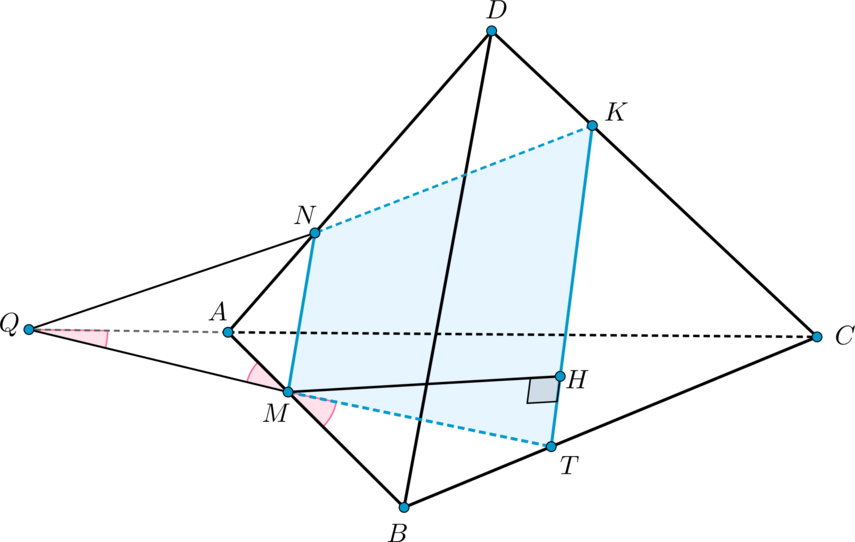
б) По теореме Менелая для $△ADC$ и прямой $QK$ имеем:

$AN-- ⋅ DK- ⋅ CQ-= 1 ⇒ QA = 8 N D KC QA$

По условию $AM = 13AB = 8$ . Т.к. $QA = AM$ и $∠CAB = 60∘ ⇒ ∠AQM = 30∘$ . Следовательно, $∠BM T = 30∘$ , тогда $∠M T B = 90∘$ . Следовательно, $BT = 8$ . Заметим, что $△N DK = △M BT$ по углу и двум прилежащим сторонам, следовательно, $M T = N K$ . Также заметим, что так как $BT = DK = 8$ , то $TK ∥ DB$ . Также и $M N ∥ DB$ . Следовательно, $M N KT$ – равнобедренная трапеция.

Основания $M N = 8$ , $KT = 16$ , по теореме Пифагора $√ -------- √ -- M T = 162 − 82 = 8 3$ . Следовательно, если провести высоту $M H$ , то $T H = 0,5(16 − 8) = 4$ . Тогда по теореме Пифагора $∘ --√--------- √ --- M H = (8 3)2 − 42 = 4 11$ . Следовательно,

8-+-16- √ --- √ --- SMNKT = 2 ⋅ 4 11 = 48 11

Ответ:

б) $√ --- 48 11$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#2575

Ребра $DA, DB, DC$ пирамиды $ABCD$ попарно перпендикулярны. $√ -- AB = AC = BC = 7 2$ .

а) Докажите, что пирамида правильная.

б) Найдите площадь сечения $BM N$ , если точки $M$ и $N$ лежат на ребрах $DA$ и $DC$ соответственно, причем $DM : M A = DN : N C = 4 : 3$ .

Показать ответ и решение

а) Для того, чтобы доказать, что пирамида является правильной, нужно доказать, что в основании пирамиды находится правильный многоугольник, а боковые ребра равны.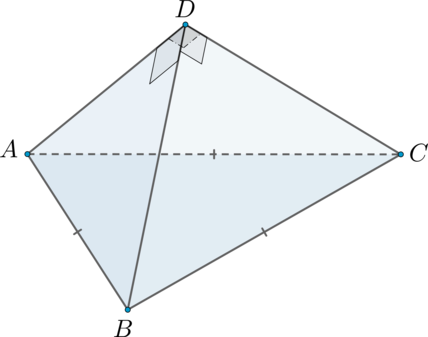
$PIC$
Возьмем за основание $△ABC$ – он правильный по условию.
Осталось доказать, что $DA = DC = DB$ .
Рассмотрим $△ADB$ и $△CDB$ . Они прямоугольные и равны по катету и гипотенузе. Следовательно, $DA = DC$ . Аналогично рассматривая другие боковые грани, доказываем, что $DA = DB$ . Следовательно, $DA = DB = DC$ , чтд.

б) Заметим, что так как $DM : M A = DN : N C = 4 : 3$ и боковые грани – равные треугольники, то $BM = BN$ . $PIC$
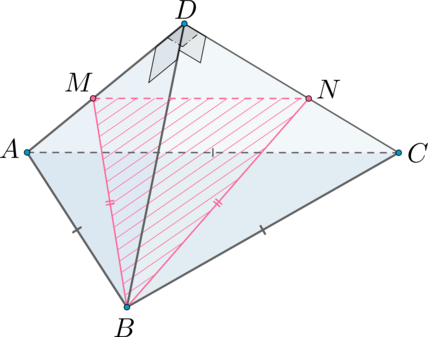
Так как $DM : M A = DN : N C = 4 : 3$ , то по теореме Фалеса $M N ∥ AC$ , также $△DM N ∼ △DAC$ .
Из подобия следует:

M N DM 4 4 √ -- -----= -----= -- → M N = -AC = 4 2 AC DA 7 7

Найдем $BM$ .
Так как $△ADB$ прямоугольный и равнобедренный, то $√ -- DA = DB = AB : 2$ , следовательно, $DA = 7$ .
Рассмотрим прямоугольный $△DM B$ . Так как $4 DM = 7DA = 4$ , то $√ -2---2- √ --- BM = 4 + 7 = 65$ .
Рассмотрим теперь $△BM N$ : $PIC$
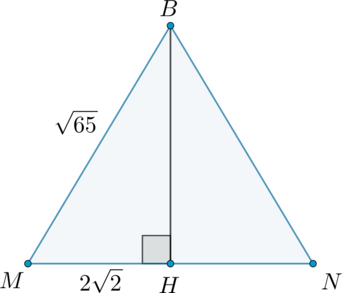
Так как он равнобедренный, то высота $BH$ , проведенная к основанию, будет также и медианой. Следовательно,

√ ------- √ --- BH = 65 − 8 = 57

Таким образом,

1 √ ---- S△BMN = --⋅ BH ⋅ M N = 2 114 2

Ответ:

б) $√ ---- 2 114$

Ошибка.
Попробуйте повторить позже

Задача 8#2369

Дана правильная четырехугольная пирамида $SABCD$ с вершиной $S$ , стороны основания которой равны $√ -- 6 2$ , а боковые ребра равны $21$ .

а) Постройте сечение пирамиды плоскостью, проходящей через точку $A$ и середину ребра $SC$ параллельно прямой $BD$ .

б) Найдите площадь построенного сечения.

Показать ответ и решение

а) Пусть $N$ – середина ребра $SC$ , $SH$ – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную $BD$ . Рассмотрим плоскость $ASC$ . Прямая $AN$ пересекает $SH$ в точке $O$ . Теперь рассмотрим $BSD$ . Проведем в этой плоскости через точку $O$ прямую, параллельную $BD$ . Пусть она пересечет ребра $SB$ и $SD$ в точках $M$ и $K$ соответственно. Таким образом, $AM N K$ – искомое сечение.

$PIC$

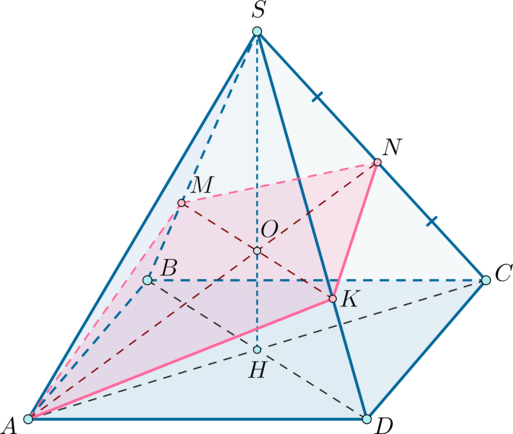
б) Заметим, что по теореме о трех перпендикулярах (так как $OH ⊥ (ABC ),AH ⊥ BD$ ) $AO ⊥ BD$ . Так как $BD ∥ M K$ , то $AO ⊥ M K$ , следовательно, $AN ⊥ M K$ . Следовательно, у четырехугольника $AM N K$ диагонали взаимно перпендикулярны. Значит, его площадь можно найти как

S = 1AN ⋅ M K. 2

Заметим сразу, что $√ -- BD = AC = AB 2 = 12$ .
Рассмотрим плоскость $ASC$ .

$PIC$

По теореме Менелая:

-SN- ⋅-CA- ⋅ HO- = 1 ⇒ HO--= 1- ⇒ OS = 2OH ⇒ SO--= 2. N C AH OS OS 2 SH 3

(это нам понадобится позже для поиска $M K$ )

Проведем $N Q ⊥ AC$ . Тогда из подобия $△SHC$ и $△N QC$ :

√ ------------ √-------- √ ------ SH-- = SC--= 2 ⇒ N Q = 1SH = 1- SC2 − HC2 = 1- 212 − 62 = 1- 81 ⋅ 5 N Q N C 2 2 2 2

$Q$ – середина $HC$ , следовательно, $3 3 AQ = 4AC = 4 ⋅ 12 = 9$ . Тогда по теореме Пифагора

∘ ------------ ∘ ----------- AN = AQ2 + N Q2 = 81-⋅ 5-+ 81 = 27-. 4 2

Рассмотрим $BSD$ . Так как $△M SK ∼ △BSD$ , то

M K SO 2 2 2 -----= ----= -- ⇒ M K = -BD = --⋅ 12 = 8. BD SH 3 3 3

Следовательно, площадь сечения равна

S = 1-⋅ 8 ⋅ 27-= 54. 2 2

Ответ: б) 54

Ошибка.
Попробуйте повторить позже

Задача 9#1678

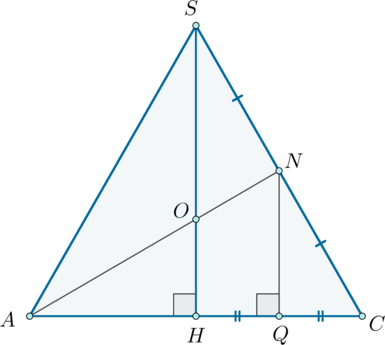
Дана правильная треугольная пирамида $SABC$ с вершиной $S$ . Проведите плоскость через середину ребра $AC$ и точки пересечения медиан граней $ASB$ и $CSB$ . Найдите площадь сечения пирамиды этой плоскостью, если $-- AB = 21, AS = 12√ 2$ .

Показать ответ и решение

1) Пусть $K$ – середина $AC$ , $SX, AL$ – медианы грани $ASB$ , $CL, SY$ – медианы грани $CSB$ , $AL ∩ SX = M, CL ∩ SY = N$ . $SO$ – высота пирамиды.

Найдем сечение пирамиды плоскостью $M N K$ .
Т.к. пирамида правильная, то $△SXY$ – равнобедренный, $2 SM = SN = -SX ⇒ M N ∥ XY ⇒ M N ∥ (ABC ) 3$ . Таким образом, плоскость $M N K$ содержит прямую $M N$ , параллельную $ABC$ , следовательно, плоскость $M N K$ пересечет плоскость $ABC$ по прямой, параллельной $M N$ (если это не так, то линия пересечения этих плоскостей $l ∩ M N = E ⇒ E ∈ (ABC )$ и $E ∈ M N ⇒ M N$ не может быть параллельна $(ABC )$ ).

$PIC$

Прямая, проходящая через точку $K$ и параллельная $M N$ (или $XY$ ) – это $AC$ . Следовательно, сечением является равнобедренный треугольник $ALC$ .

2) Пусть $LK ∩ SO = H$ . Тогда по теореме о трех перпендикулярах $HK ⊥ AC$ как наклонная ( $HO ⊥ (ABC ),OK ⊥ AC$ как проекция). Следовательно, и $LK ⊥ AC$ .

Тогда $1- SALC = 2AC ⋅ LK$ .

$PIC$

Рассмотрим $√ -- √ -- √ -- △SKB : BK = AB ⋅--3-= 21--3-⇒ cosB = -7√-3- 2 2 12 2$ .

Тогда по теореме косинусов для $△KLB$ :

$2 729- 27- KL = 4 ⇒ KL = 2$

Значит, $SALC = 567- 4$ .

Ответ:

$567 ---- 4$ .

Ошибка.
Попробуйте повторить позже

Задача 10#1327

$ABCA1B1C1$ - прямая треугольная призма, $AB = 16, BC = 15, AA1 = 8$ , $cos∠ABC = 0,8$ . $M, N$ – середины ребер $AC$ и $B1C1$ соответственно. $K, P$ – такие точки на ребрах $BC$ и $B1C1$ соответственно, что $1- CK = B1P = 6BC$ .

а) Построить сечение призмы плоскостью $α$ , параллельной прямой $M N$ и проходящей через точки $K$ и $P$ .

б) Найти площадь сечения призмы плоскостью $α$ .

Показать ответ и решение

а) $PIC$

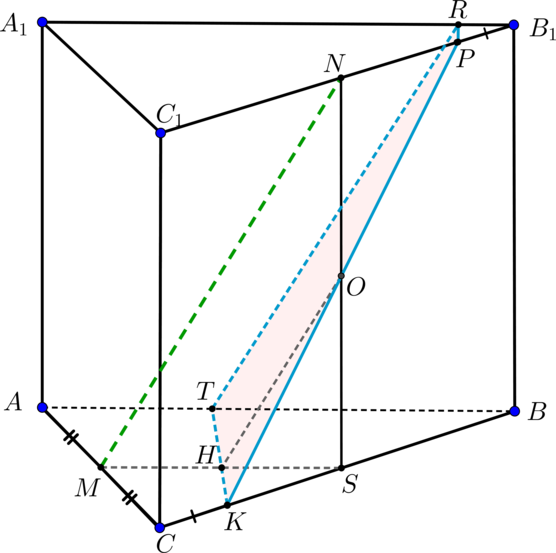
Если прямая $M N ∥ α ⇒ M N$ параллельна некоторой прямой, лежащей в $α$ . Проведем $N S ⊥ BC, N S ∩ KP = O$ . В плоскости $M N S$ проведем $OH ∥ M N ⇒ M H = HS$ . Тогда прямая $KH ∩ AB = T$ . Так как плоскости $ABC$ и $A1B1C1$ параллельны, то $α$ пересечет плоскость $A1B1C1$ по прямой, параллельной $KT$ . Следовательно, проведем $P R ∥ KT$ . Таким образом, $TRP K$ – искомое сечение (трапеция).

б) Заметим, что $1 5 CK = --⋅ 15 =--⇒ KS = 5 6 2$ . Т.к. $M S$ – средняя линия треугольника $ABC ⇒ M S = 8 ⇒ HS = 4$ . Так как $∠HSK = ∠ABC$ , то по теореме косинусов $∘ -------------------- HK = 16 + 25 − 2 ⋅ 4 ⋅ 5 ⋅ 45 = 3$ . Таким образом, по обратной теореме Пифагора треугольник $HKS$ – прямоугольный, следовательно, $∠H = 90 ∘$ . Таким образом, по теореме о трех перпендикулярах, из того, что $N S ⊥ (ABC ),HS ⊥ KT ⇒ OH ⊥ KT$ .

Проведем $P H1 ⊥ KT$ . Из подобия треугольников $HOK$ и $H1P K$ следует, что $P H1 = 2OH$ . Т.к. $1- √ -- OS = 2N S = 4,HS = 4 ⇒ OH = 4 2$ . Таким образом найдена высота трапеции $√ -- P H1 = 8 2$ .

$PIC$

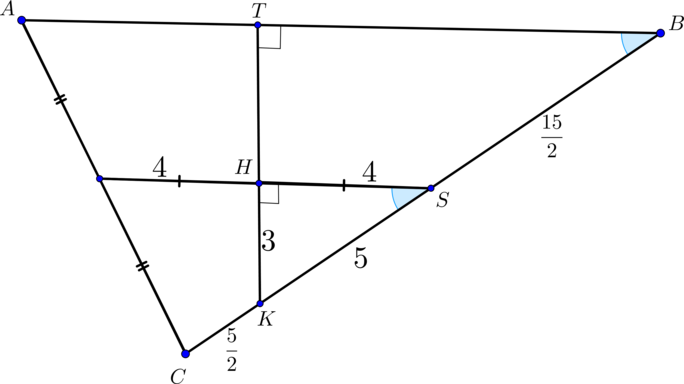
Найдем основания трапеции $KT$ и $P R$ .

$sin ∠KSH = 3-= sin ∠B = KT-- ⇒ KT = 15- 5 KB 2$ .

$3 △ PRB1 ∼ △KT B ⇒ P R = -- 2$ .

Таким образом, $( ) 1- 15- 3- √ -- √ -- STRP K = 2 ⋅ 2 + 2 ⋅ 8 2 = 36 2$

Ответ:

б) $√ -- 36 2$

Ошибка.
Попробуйте повторить позже

Задача 11#1716

Дана правильная шестиугольная пирамида $SABCDEF$ , сторона основания которой равна $a = 4$ , боковое ребро $b = 7$ , $SO$ – высота. Через точку $L$ ( $SL : LO = 3 : 1$ ) проведена плоскость $α$ параллельно грани $SAB$ .

а) Доказать, что плоскость $α$ пересекает ребро $SD$ в точке $K$ , где $SK : KD = 3 : 5$ .

б) Найти площадь сечения пирамиды плоскостью $α$ .

Показать ответ и решение

а) $PIC$

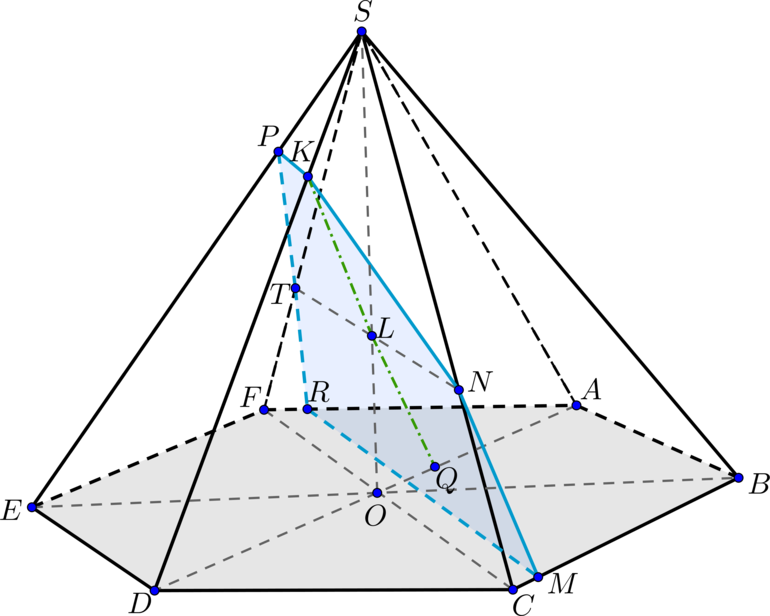
Две плоскости параллельны, если две пересекающиеся прямые из одной плоскости будут параллельны некоторых двум пересекающимся прямым из другой плоскости.Проведем через точку $L$ прямые, параллельные $AB$ и $AS$ .
Из свойства правильного шестиугольника следует, что $F C ∥ AB$ . Проведем в плоскости $F SC$ через точку $L$ : $T N ∥ F C$ .

Тогда по теореме Фалеса $SN ST SL 3 ----= ----= ----= -- N C TF LO 1$

В плоскости $ASD$ проведем через точку $L$ : $KQ ∥ SA$ .

Из теоремы Фалеса следует, что $AQ SL 3 ----= ----= -- QO LO 1$

Пусть $AQ = 3x,QO = x$ . Из свойств правильного шестиугольника следует, что $DO = OA = 4x$ .

Тогда по теореме Фалеса $DQ--= DK-- = 5x-= 5- QA KS 3x 3$

б) Достроим сечение пирамиды плоскостью $α$ . Плоскость $α$ пересечет плоскость основания по прямой $RM ∥ AB, Q ∈ RM$ . Значит, $BM--- AR-- 3- M C = RF = 1$

Аналогично, плоскость $α$ пересекает грань $SED$ по прямой $PK ∥ ED ∥ AB$ . Таким образом, $M N KP TR$ – сечение.
Заметим, что сечение представляет собой две равнобокие трапеции $M N T R$ и $N KP T$ .

$PIC$

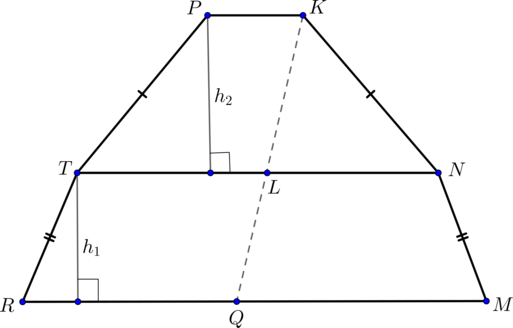
Найдем все их стороны.
Из подобия $3 3 △ ST N ∼ △SF C ⇒ TN = -F C = -a = 6 4 2$
Из подобия $△ CN M ∼ △CSB ⇒ N M = 1-b = 7- 4 4$

Достроим трапецию $F ABC$ до треугольника $F W C$ – он правильный. $7 7 ⇒ RM = -F C = -a = 7 8 4$
Из подобия $3 3 3 △ SP K ∼ △SED ⇒ P K = -ED = --a = -- 8 8 2$