Ошибка.
Попробуйте повторить позже
Мало кто знает, но в своё время Дед Мороз тоже закончил мехмат МГУ — Мурманского Государственного Университета! В ту эпоху ЕГЭ ещё не было и для поступления Дед Мороз сдавал внутренние вступительные экзамены.
Дан куб в который вписан шар с центром в точке
На
диагонали
отмечена точка M так, что
Точка
—
середина диагонали
а) Докажите, что центр шара принадлежит плоскости
б) Из точек и
опустили перпендикуляры
и
на плоскость
Найдите объём пирамиды
если ребро куба равно
8.
Попробуйте решить оба пункта, и кто знает, возможно, и вы однажды станете студентом МГУ!!!
а)
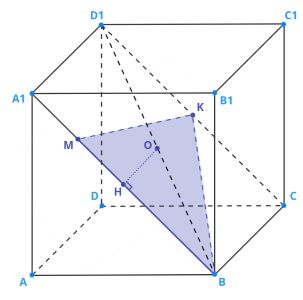
1. Шар вписан в куб, центром этих фигур является одна и та же точка, поэтому работать будем именно с центром куба. Центр куба — точка пересечения его диагоналей.
2. Пусть — середина диагонали
Теперь следует доказать, что точка
принадлежит плоскости
3. Диагональ лежит в плоскости
В этой же плоскости лежат и
три точки плоскости
то есть точка
лежит в той же плоскости, что и
все точки
Ч.Т.Д.
б)
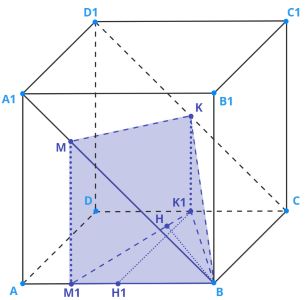
1. Проведём перпендикуляр к прямой
2. следовательно,
перпендикулярно любой прямой,
лежащей в плоскости
то есть
3. и
означают, что
То есть
— высота пирамиды. Найдем её длину через метод площадей для
4. Проведём перпендикуляр к
Его длина равна длине стороны
так как
— прямоугольник.
5. Из подобия , получаем
откуда поскольку
— куб, у него все
рёбра равны.
6. Аналогично находим, что откуда
и
— середины
сторон
и
соответственно.
7. По теореме Пифагора для
8. По методу площадей для вычислим высоту
9. Основание пирамиды — четырёхугольник Прямые
и
перпендикулярны плоскости
значит они параллельны и
на самом деле — трапеция.
10. Из тезисов и
выводим, что
То есть
— высота трапеции.
11. Найдём площадь основания пирамиды:
12. Найдём объём пирамиды:
Ошибка.
Попробуйте повторить позже
Найдите диаметр сферы, описанной около правильного тетраэдра с ребром, равным .
Рассмотрим правильный тетраэдр и описанную около него сферу с центром
и радиусом
. Центр сферы, описанной около
правильной треугольной пирамиды, лежит на прямой, содержащей высоту пирамиды. Следовательно, точка
лежит на прямой
.
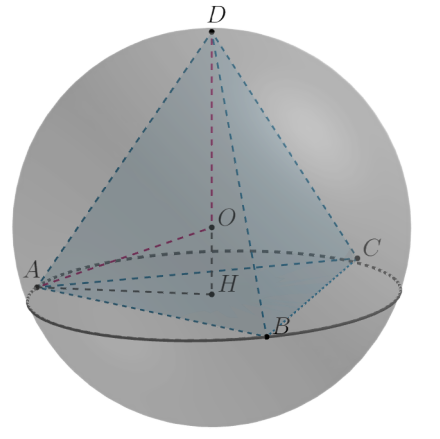
Рассмотрим треугольник : он прямоугольный, катет
равен
от высоты правильного треугольника
, следовательно,
. Тогда по теореме Пифагора из
:
Центр сферы, описанной около правильного тетраэдра, лежит на отрезке (так как
, то точка
,
лежащая на прямой
и равноудаленная от точек
и
, лежит на отрезке
). Рассмотрим
. По теореме
Пифагора
Ошибка.
Попробуйте повторить позже
Докажите, что площадь боковой поверхности конуса вычисляется по формуле
где — радиус основания конуса, а
— длина его образующей.
Разрежем конус по обращующей и развернем его боковую поверхность, чтобы получилась плоская фигура. Тогда мы получим
круговой сектор радиуса
с длиной дуги
. Пусть
— угол, опирающийся на дугу кругового сектора.
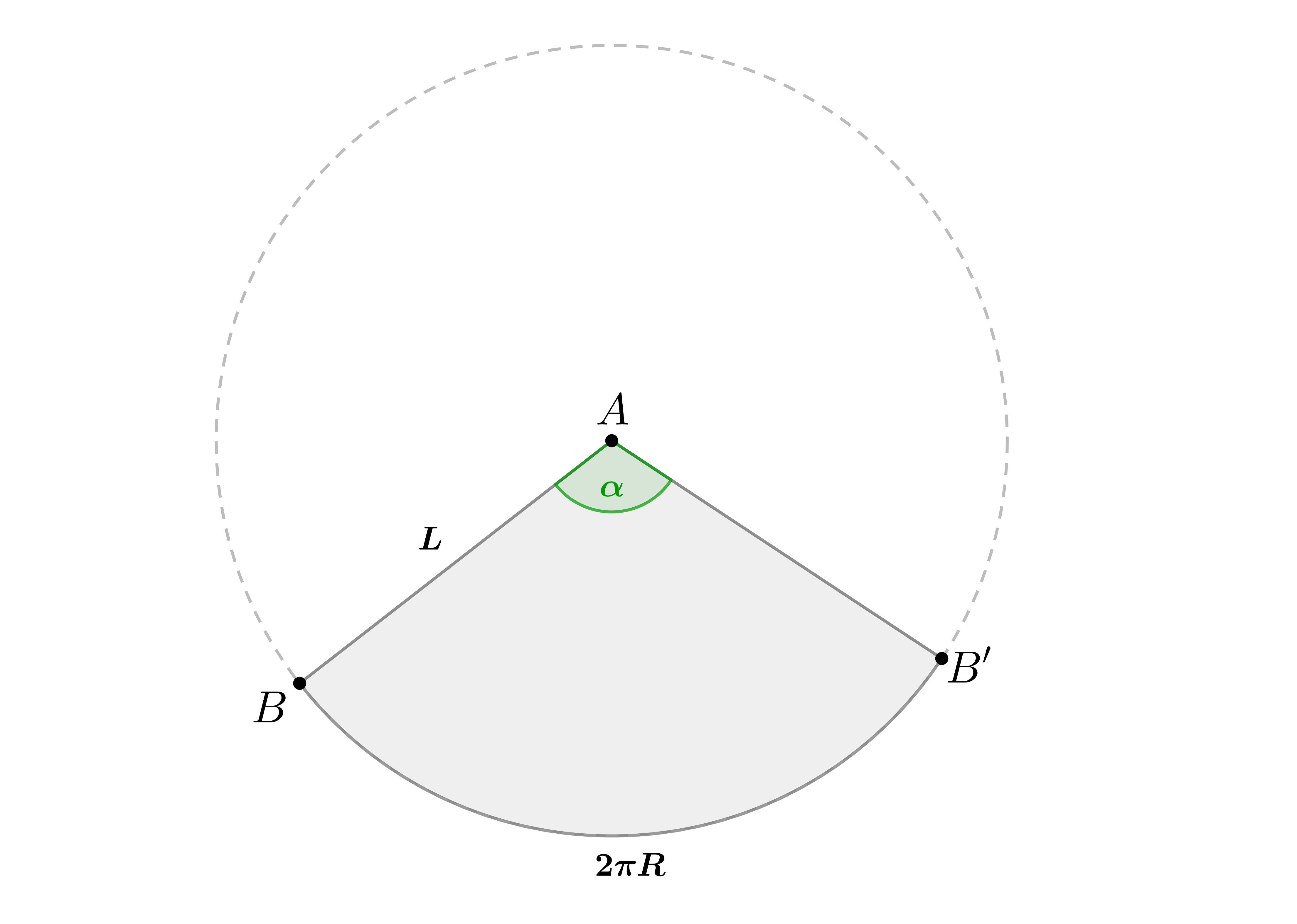
Длина дуги с одной стороны равна
, а с другой стороны, так как круговой сектор — это часть круга радиуса
, длина дуги,
образованной центральным углом
, равна
Отсюда
Тогда площадь боковой поверхности конуса равна площади кругового сектора и равна
Ошибка.
Попробуйте повторить позже
Докажите, что площадь боковой поверхности цилиндра вычисляется по формуле
где — радиус основания цилиндра, а
— его высота.
Разрежем цилиндр по образующей и развернем его так, чтобы получилась плоская фигура. Тогда мы получим развертку
цилиндра. Так как образующие цилиндра перпендикулярны плоскостям оснований, то мы получим прямоугольник, одна
сторона которого равна длине окружности основания, то есть
, а другая —- высоте цилиндра. Отсюда получаем, что

Ошибка.
Попробуйте повторить позже
Докажите, что радиус круга, являющегося сечением конуса плоскостью, параллельной основанию, относится к радиусу основания конуса с коэффициентом, равным отношению расстояния от вершины конуса до секущей плоскости к высоте конуса.
Рассмотрим осевое сечение конуса. Пусть в осевом сечении — радиус основания конуса,
— радиус сечения
конуса.
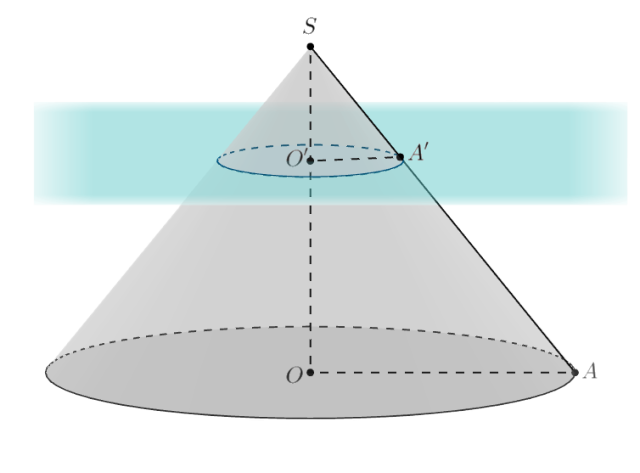
Так как секущая плоскость параллельна основанию, а перпендикулярно плоскости основания конуса, то
перпендикулярно
плоскости сечения. Тогда прямоугольные
по двум углам. Отсюда
Чтд.
Ошибка.
Попробуйте повторить позже
Найдите угол при вершине осевого сечения конуса, если известно, что на его поверности можно провести три попарно перпендикулярные образующие.
Рассмотрим конус. Пусть — попарно перпендикуллярные образующие. Тогда
— равнобедренные
прямоугольные треугольники.
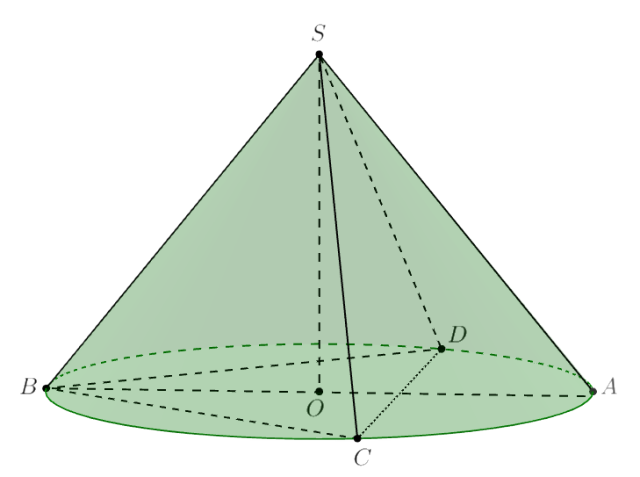
Пусть образующая . Тогда
. Правильный
— вписанный в окружность с диаметром
, следовательно, по
теореме синусов
Рассмотрим осевое сечение — это равнобедренный треугольник. По теореме косинусов
Ошибка.
Попробуйте повторить позже
Найдите ребро куба, одна грань которого принадлежит основанию конуса, а а вершины оставшихся граней расположены на его боковой
поверхности, если радиус основания конуса равен , а высота равна
Рассмотрим рисунок. Из условия следует, что ,
.
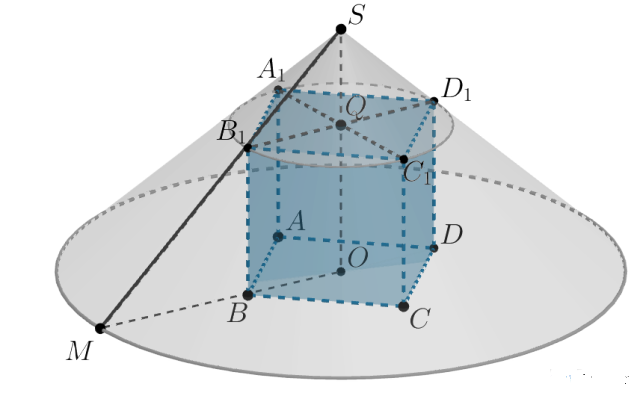
Пусть , тогда из
следует, что
Ошибка.
Попробуйте повторить позже
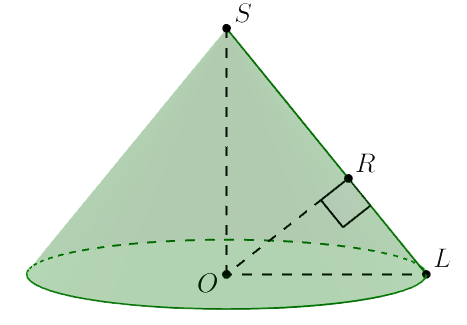
Докажите, что объем конуса равен третьей части произведения боковой поверхности на расстояние от центра основания до образующей.
Известно, что . Рассмотрим прямоугольный
:
, следовательно,
Ошибка.
Попробуйте повторить позже
Два равных конуса имеют общую высоту. Плоскости их оснований параллельны. Докажите, что объем их общей части равен четверти объема каждого из них.
Конусы пересекаются по окружности. В силу симметрии точек и
относительно этой окружности, она равноудалена от этих точек на
расстояние, вдвое меньшее высоты конусов.
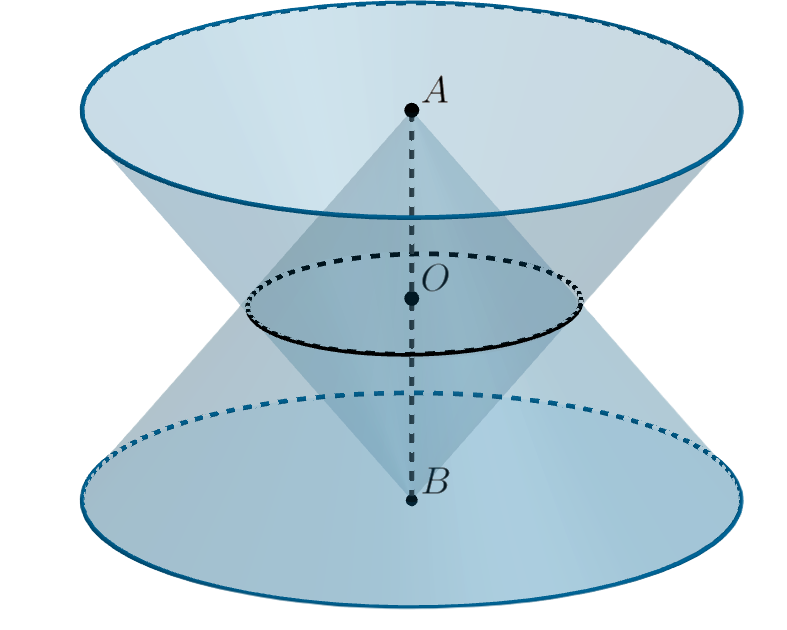
Общая часть конусов состоит из двух конусов, вершины которых — точки и
, а основание — окружность пересечения.
Рассмотрим конусы с вершиной и основаниями-окружностями с центрами в
и
. Так как высота меньшего конуса вдвое меньше
высоты большего конуса, то радиус основания меньшего конуса также вдвое меньше радиуса основания большего конуса, следовательно,
объем меньшего конуса в 8 раз меньше объема большего конуса. Аналогично объем конуса с вершиной
и основанием-окружностью с
центром в точке
в 8 раз меньше объема большего конуса. Следовательно, объем общей части составляет
объема большего
конуса.
Ошибка.
Попробуйте повторить позже
Докажите, что если в четырехгранный угол можно вписать сферу, то суммы противоположных плоских углов четырехгранного угла равны.
Пусть плоские углы четырехгранного угла равны ,
,
,
.
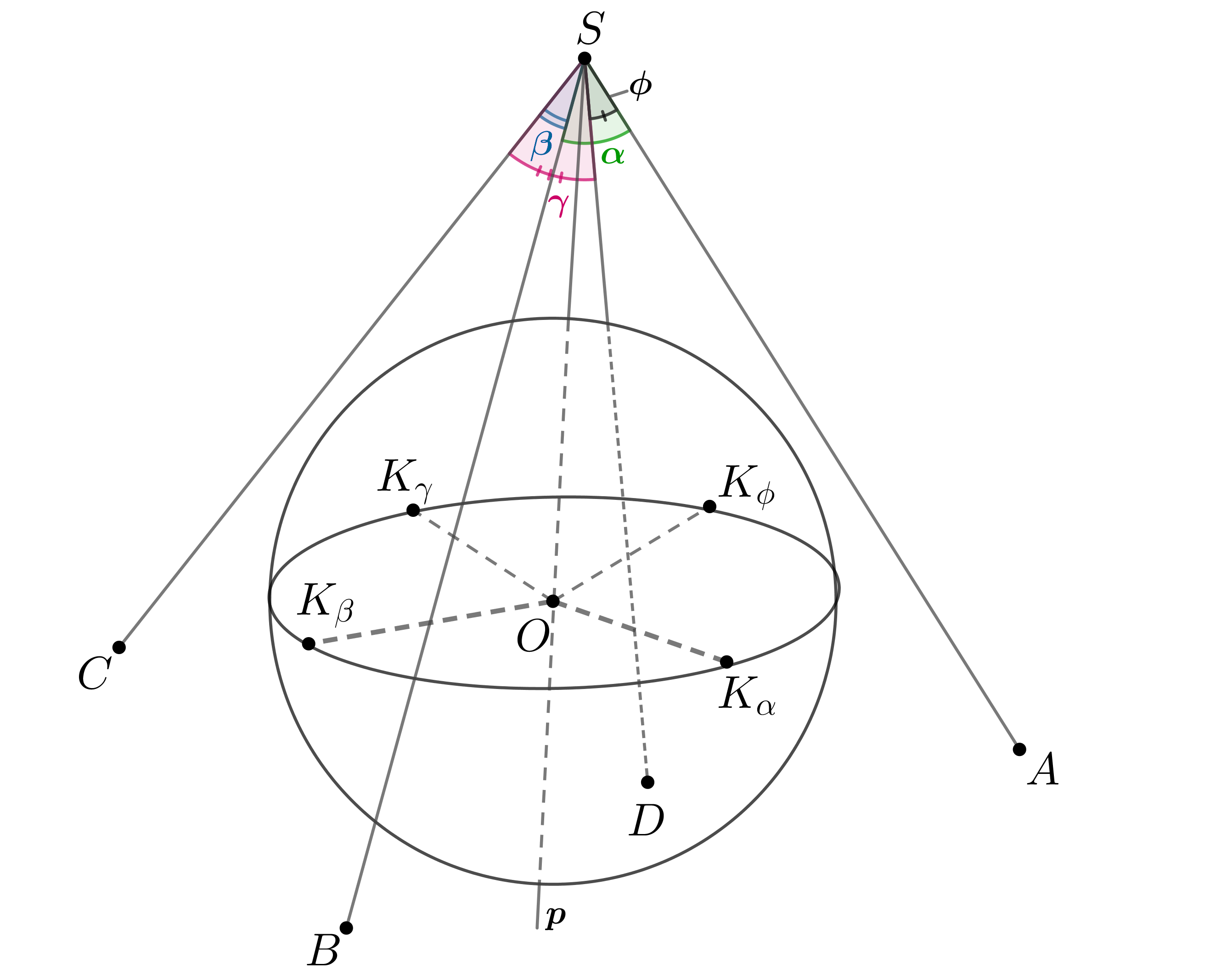
Пусть сфера касается граней четырехгранного угла в точках ,
,
,
(как показано на рисунке). Так как
и
симметричны относительно плоскости
, то
. Аналогично
,
,
. Следовательно,
Чтд.
Ошибка.
Попробуйте повторить позже
Через точку , расположенную вне сферы, проведены две прямые. Одна из них касается сферы в точке
, а вторая пересекает ее в
точках
и
. Докажите, что
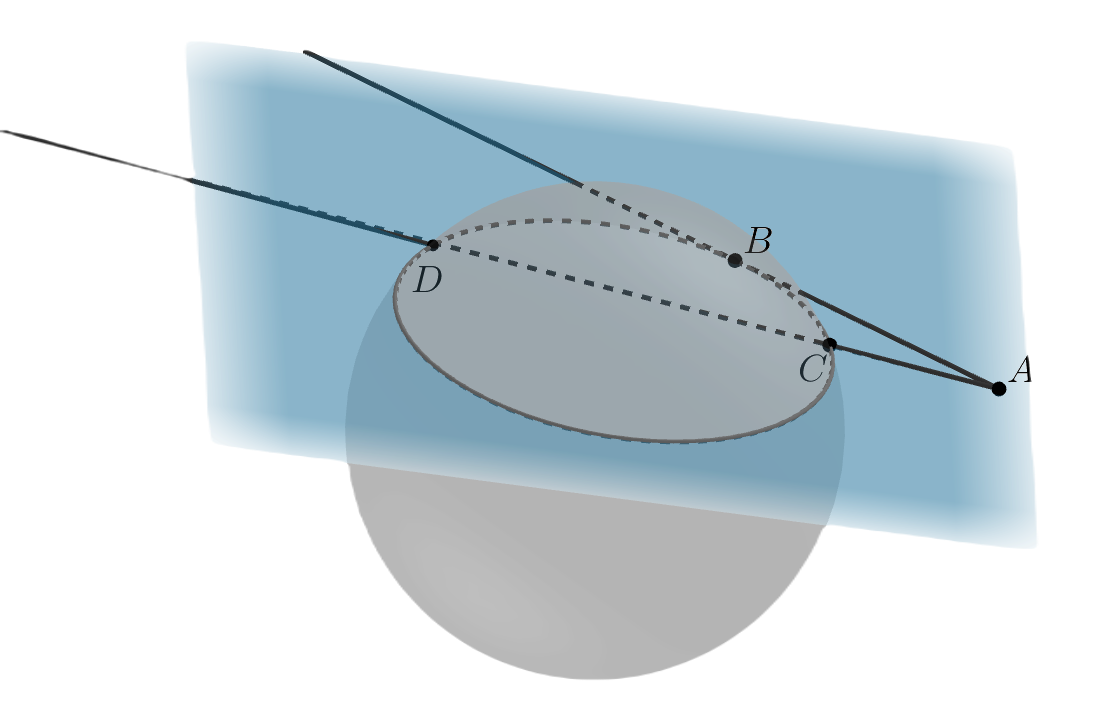
Проведем плоскость через прямые и
. Сечение сферы этой плоскостью — окружность. Тогда
— касательная к этой
окружности,
— секущая. Так как квадрат отрезка касаетельной равен произведению секущей на ее внешнюю часть, то
Ошибка.
Попробуйте повторить позже
Даны плоскость и перпендикулярная ей прямая
. Найдите геометрическое место центров шаров, касающихся одновременно плоскости
и прямой
Проведем прямую . Найдем расстояние между прямыми
и
— оно равно отрезку
(где
и
— точки пересечения
и
соответсвенно с плоскостью
).
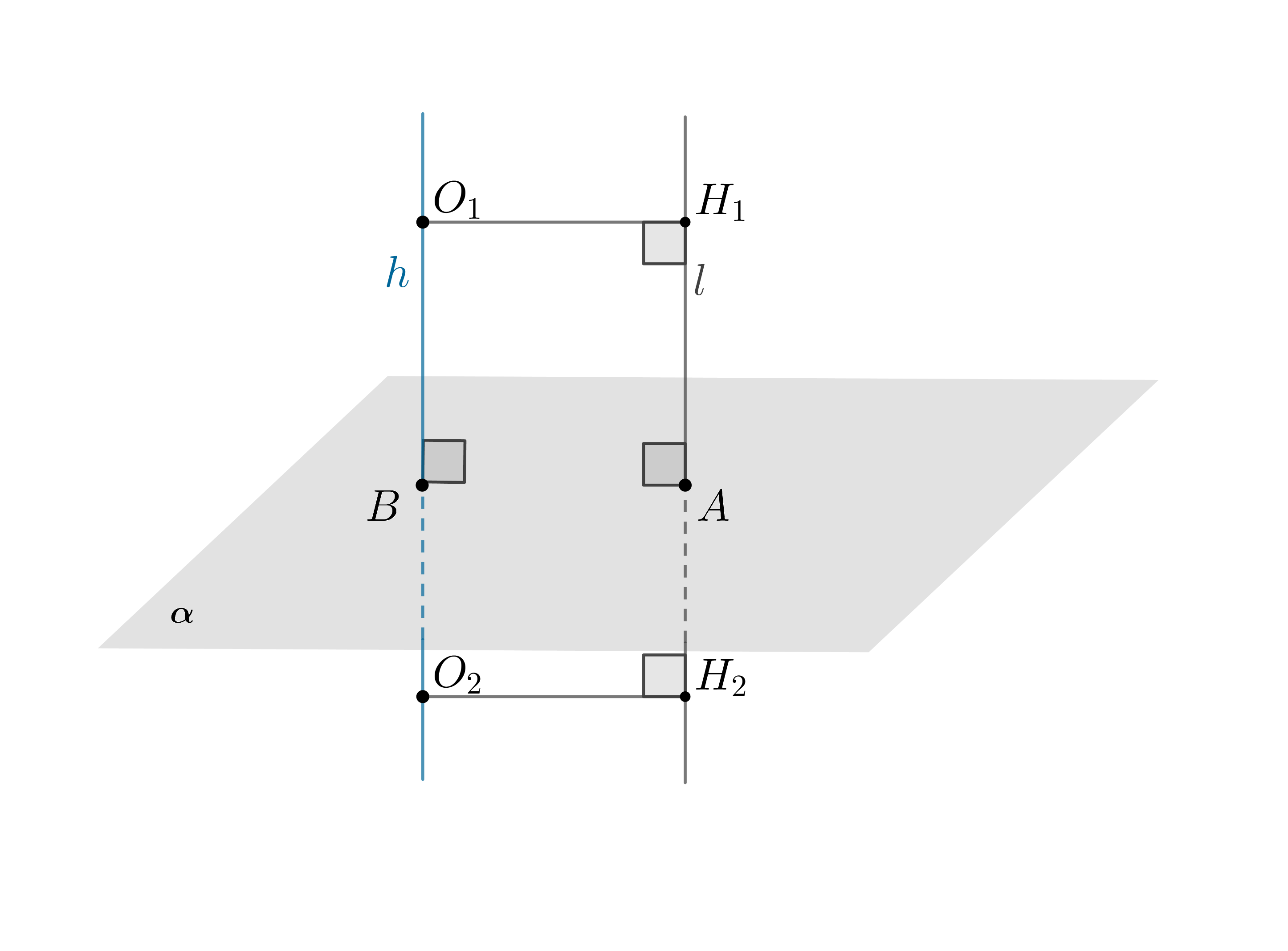
Если отметить две точки и
на прямой
таким образом, чтобы
, то эти точки будут равноудалены от
плоскости и от прямой
, следовательно, сфера с центром в одной из этих точек будет равноудалена от плоскости
и прямой
.
Таким образом, ГМТ — множество противоположных точке вершин квадратов, построенных так, что одна из сторон квадратов лежит
на прямой
, а радиус сферы равен стороне квадрата.
Вершины этих квадратов — точки основания конусов, центр которых лежит на прямой
, вершина конусов — точка
, а радиус
основания равен радиусу сферы. Следовательно, получаем, что
лежит на поверхности двух бесконечных конусов, угол между осью и
образующей которых равен
, ось которых — прямая
, а вершина — точка
.
Ошибка.
Попробуйте повторить позже
Докажите, что если около параллелепипеда можно описать сферу, то этот параллелепипед — прямоугольный.
Рассмотрим параллелепипед . Пусть
— равноудалена от всех вершин параллелепипеда. Для пирамиды
эта сфера также является описанной, следовательно, около
можно описать окружность (
— ее центр,
). Если около параллелограмма можно описать окружность, то он — прямоугольник, следовательно,
—
прямоугольник. Аналогично доказывается, что все остальные грани — прямоугольники. Следовательно, параллелепипед
прямоугольный.
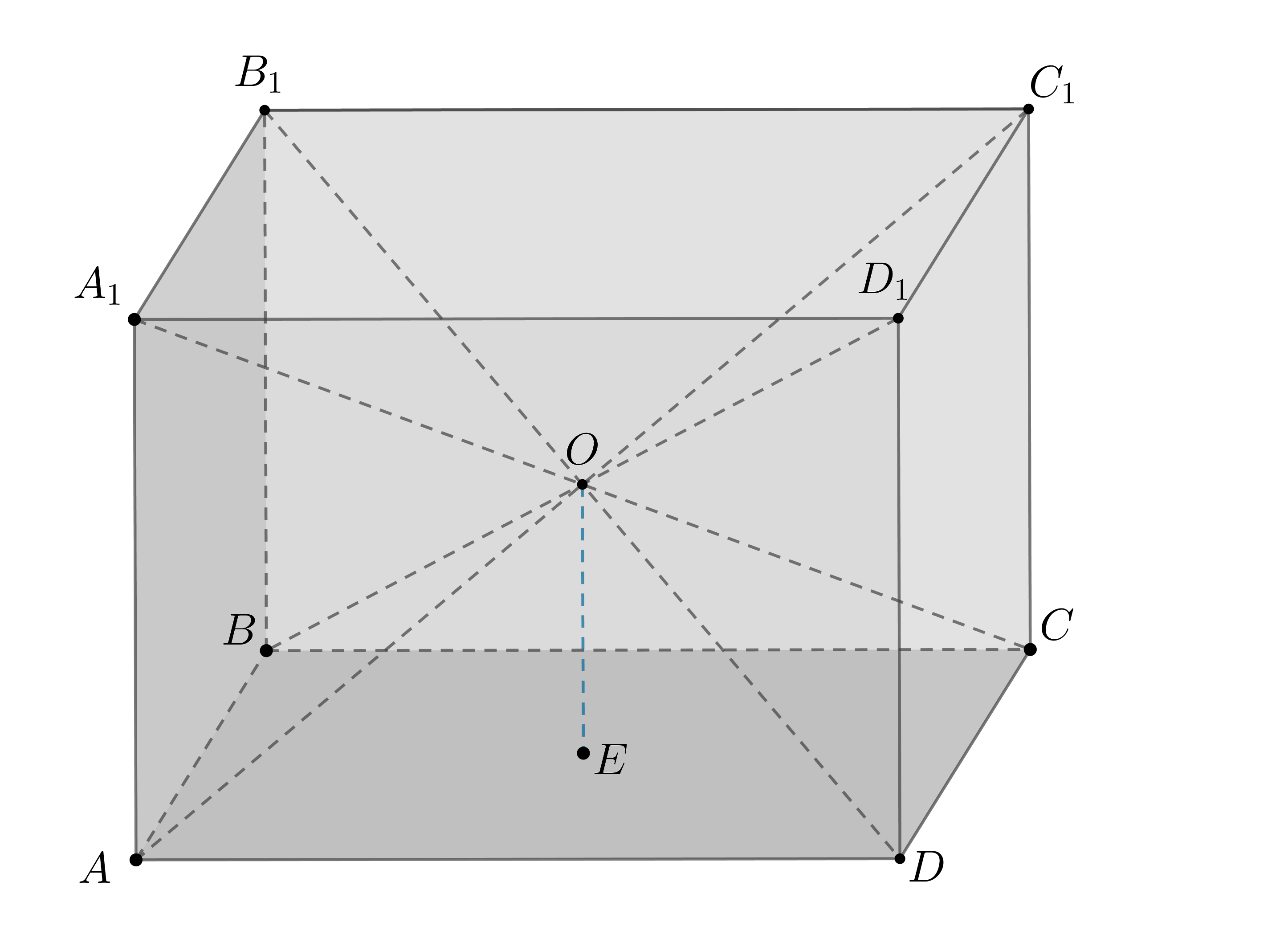
Заметим, что — точка пересечения диагоналей параллелепипеда. Действительно, диагонали прямоугольного параллелепипеда
равны и точкой пересечения делятся пополам. Следовательно, точка пересечения диагоналей равноудалена от всех вершин
параллелепипеда.
Ошибка.
Попробуйте повторить позже
Найдите ребро куба, вписанного в сферу радиуса
Центр сферы, описанной около куба, — это точка пересечения диагоналей куба. Действительно, проведем две произвольные диагонали
и
. Пусть они пересекаются в точке
.
, откуда
. Следовательно,
— середина этих диагоналей. А так как диагонали куба равны, то
равноудалена от вершин
. Так как это две произвольные
диагонали, то
равноудалена от всех вершин куба.
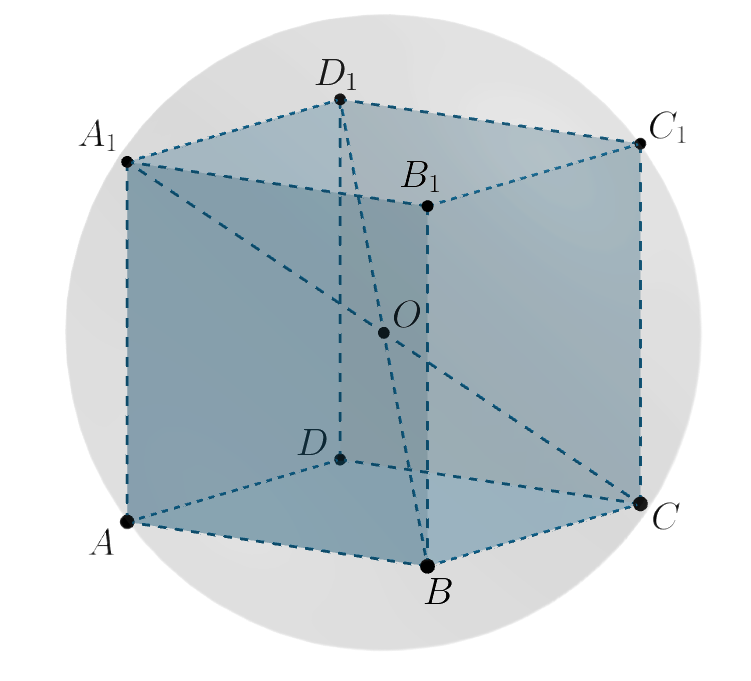
Таким образом, , откуда
, следовательно,
— ребро куба.
Ошибка.
Попробуйте повторить позже
Докажите, что около пирамиды можно описать сферу тогда и только тогда, когда около основания этой пирамиды можно описать окружность.
Возьмем пирамиду .
Докажем, что если около пирамиды описана сфера, то около основания пирамиды можно описать окружность. Пусть
—
центр сферы. Тогда точка
равноудалена от вершин пирамиды. Проведем
Тогда
как прямоугольные по общему катету и гипотенузе. Следовательно,
. Следовательно,
равноудалена от вершин
основания, следовательно, это центр описанной около основания окружности.

Докажем, что если около основания пирамиды можно описать окружность, то можно описать сферу около этой пирамиды.
Пусть
— центр окружности, описанной около
. Через точку
проведем прямую
. Тогда для
любой точки
этой прямой верно
. Отметим точку
таким образом, чтобы
был
равнобедренным, то есть
. Тогда
, следовательно,
— центр описанной около пирамиды
сферы.
Ошибка.
Попробуйте повторить позже
Докажите, что плоскость , проходящая через образующую цилиндра, является касательной к нему тогда и только тогда, когда она
перпендикулярна осевому сечению цилиндра, проведенному через эту образующую.
(Плоскость называется касательной к цилиндру, если она проходит через его образующую и не имеет с ним других общих точек.)
Докажем, что касательная к цилиндру плоскость
перпендикулярна осевому сечению цилиндра, проведенному через ту же
образующую
, что и
.
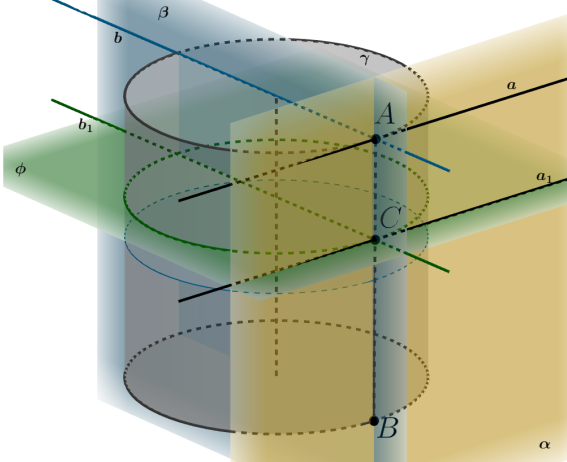
Пусть проходит через образующую
и не имеет с конусом других общих точек. Пусть
— плоскость осевого
сечения цилиндра, проходящая через
. Пусть
— плоскость верхнего основания цилиндра,
,
. Так
как
проходит через точку
верхнего основания и не имеет с ним других общих точек, прямая
— касательная к
верхнему основанию. Прямая
содержит диаметр верхнего основания, проходящий через
. Так как диаметр окружности,
проведенный в точку касания, перпендикулярен касательной, то
. Кроме того,
, откуда
. Значит,
Чтд.
Докажем, что плоскость
, проходящая через образующую
перпендикулярно осевому сечению цилиндра,
проведенному через
, является касательной к цилиндру, то есть не имеет с ним никаких общих точек, кроме точек образующей
.
Пусть — плоскость осевого сечения цилиндра, проходящая через
. Пусть
— плоскость, перпендикулярная
и
пересекающая цилиндр. Сечения цилиндра плоскость
— круг Circle, равный основаниям цилиндра (так как
параллельна плоскостям
оснований цилиндра).
, прямая
содержит диаметр
круга Circle,
, причем
,
. Из
следует, что
— касательная к Circle, то есть
— единственная общая точка
и Circle. Так как плоскость
была выбрана
произвольно (может проходить через любую точку образующей
), получаем, что
не имеет с цилиндром общих точек, не лежащих на
Чтд.
: 1)
; 2)
,
.
Ошибка.
Попробуйте повторить позже
Докажите, что в цилиндр можно вписать шар тогда и только тогда, когда высота цилиндра равна диаметру
его
основания.
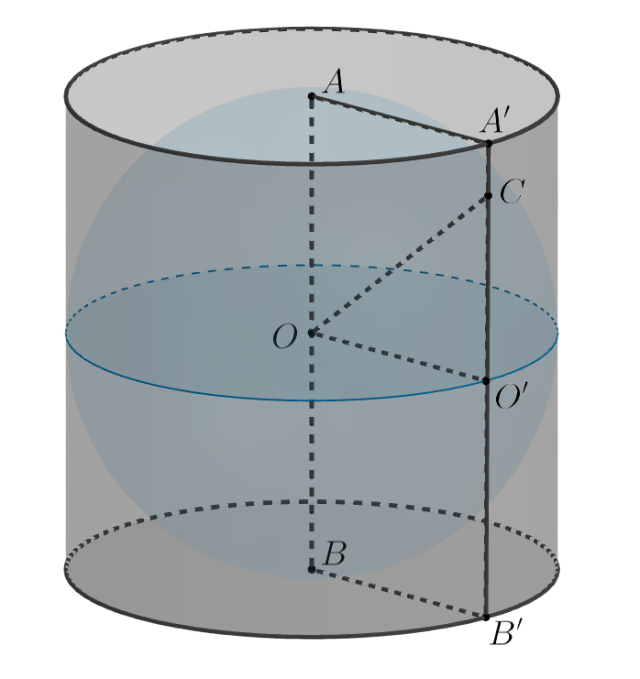
Докажем, что если в цилиндр вписан шар, то высота цилиндра равна диаметру основания цилиндра.
Если шар вписан в цилиндр, то он касается кругов-оснований цилиндра в их центрах, то есть в точках и
, и касается всех
образующих цилиндра.
Так как перпендикулярна основаниям цилиндра и каждая точка высоты
равноудалена от двух противоположных
образующих цилиндра, то центр
шара находится на отрезке
, причем в его середине. Следовательно, радиус шара
Так как отрезки касательных, проведенных из одной точке вне шара в шару, равны, то если — точка касания шара и образующей
, то
и
. Отсюда
. Чтд.
Докажем, что если высота цилиндра равна диаметру основания цилиндра, то есть
, то в цилиндр можно вписать
шар.
Докажем, что центр шара, вписанного в цилиндр, лежит в середине отрезка , а диаметр шара равен диаметру основания
цилиндра.
Пусть — середина
,
— центры оснований цилиндра. Так как
перпендикулярна основаниям цилиндра, то точка
равноудалена от оснований цилиндра, причем на расстояние
. Пусть
— середина образующей
. Тогда
—
квадрат, следовательно,
. Расстояние от точки
до любой точки
образующей
, отличной от точки
,
будет больше
, так как отрезок
является гипотенузой в прямоугольном треугольнике
. Следовательно,
если взять шар с центром в точке
и радиусом
, то образующая
будет касательной к этому шару.
Так как образующую мы выбрали произвольно, получаем, что любая образующая цилиндра касается полученного шара.
Чтд.
Ошибка.
Попробуйте повторить позже
Найдите геометрическое место всех шаров данного радиуса , касающихся граней данного двугранного угла.
Пусть полуплоскости и
— грани двугранного угла. Отметим произвольную точку
на ребре
двугранного угла и проведем через
нее плоскость
. Тогда
,
. Получили линейный угол
данного двугранного угла. Пусть
— его
биссектриса. Тогда все точки этой биссектрисы равноудалены от сторон угла
. Отметим на биссектрисе точку
такую, чтобы
, где
,
. Тогда
— центр искомого шара и
,
— его радиусы (отрезки,
перпендикулярные плоскостями
и
).
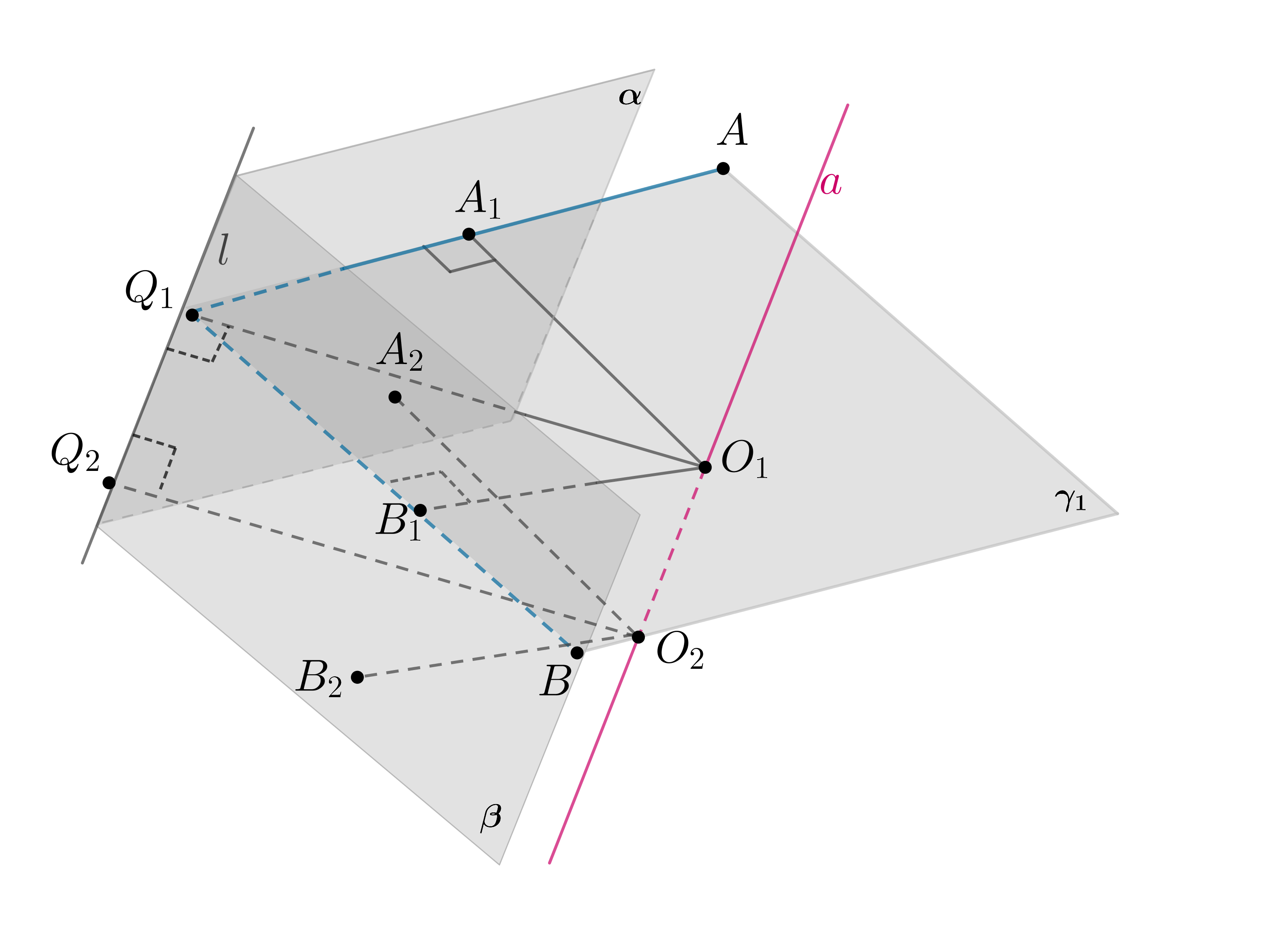
Аналогично построим ,
,
,
— линейный угол данного двугранного угла,
—
биссектриса этого линейного угла.
Тогда как пряомугольные по катету
и острому углу
. Следовательно,
.
Тогда — прямоугольник, так как
,
и
. Следовательно,
.
Тогда геометрическое место точек, являющихся центрами шаров радиуса , равноудаленных от
и
— это прямая
, параллельная
ребру
двугранного угла, удаленная от граней
и
двугранного угла на расстояние
Прямая , паралельная ребру
двугранного угла и удаленная на расстояние
от граней двугранного угла.



