Алгебра. Связь между множествами решений —Каталог задач по ЕГЭ - Математика

Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Алгебра. Связь между множествами решений

Тема 18. Задачи с параметром

18.05 Алгебра. Связь между множествами решений

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80266

Найдите все значения $a$ , при каждом из которых сумма длин промежутков, составляющих множество (возможно пустое) решений неравенства

(2 2 ) log2 x +4ax+ 4a − a < 2,

меньше 2.

Показать ответ и решение

Неравенство равносильно следующим неравенствам

2 2 0< (x+ 2a) − a< 4 ⇔ a <(x+ 2a)< 4+ a

(a) Если $a< 0,$ то получаем неравенство $(x+2a)2 < 4+a,$ удовлетворяющее требованию задачи, когда

4+a <1 ⇔ a< −3.

Выражение должно быть меньше $1,$ так как тогда решения будут принадлежать интервалу $(− 1− 2a; 1 − 2a)$

(b) Если же $a≥ 0,$ то получаем неравенство

√a <|x+ 2a|< √4-+a ⇔ 0< |x +2a|− √a-< √4+-a− √a

удовлетворяющее требованию задачи, когда

√4-+-a− √a-< 1 ⇔ √4-+a-<√a + 1 ⇔ a > 9 4

Ответ:

$(−∞;− 3)∪(9;+∞ ) 4$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#80094

Найдите все значения параметра $a,$ при каждом из которых система

( |{x = 3√y-− 1, y = − 3√ − x-+ 1, |( y = x+ a.

имеет единственное решение.

Показать ответ и решение

Запишем ограничения, определяющие ОДЗ:

{ y ≥ 0, − x ≥ 0.

{y ≥ 0, x ≤ 0.

Таким образом, мы рассматриваем только II четверть координатной плоскости.

Рассмотрим первое уравнение системы.

Выразим $y$ через возведение обеих частей уравнения в квадрат, но сначала перенесем $− 1$ в левую часть:

x + 1 = 3√y.

Для возведения в квадрат необходимо следующее условие: обе части уравнения должны быть равных знаков. Правая часть не меньше нуля при любых допустимых $y,$ таком случае:

(x + 1)2 = (3√y-)2,при x + 1 ≥ 0,

x2 + 2x + 1 = 9y,при x ≥ − 1,

x2 2x 1 y = --+ ---+ -,при x ≥ − 1. 9 9 9

Найдём координаты вершины параболы ( $x0$ , $y0$ ):

− b x0 = ---= − 1, 2a

−-12 2⋅(− 1) 1 y0(x0) = 9 + 9 + 9 = 0.

Для более простого построения найдём координаты точки с абсциссой $x = 2 :$

22 2 ⋅2 1 y(2) = --+ ----+ - = 1. 9 9 9

Рассмотрим второе уравнение системы.

$y = − 3√ − x-+ 1$ — функция корня, график которой инвертирован относительно осей $OX$ и $OY$ в виду наличия минусов перед $x$ и перед самим корнем. Вершина графика расположена в точке $(0;1).$

Для более простого построения найдём координаты точки графика корня с абсциссой $x = − 1$ и точки графика параболы с абсциссой $x = 2 :$

∘------ y(− 1) = − 3 − (− 1)+ 1 = − 2.

4 4 1 y(2) = 9 + 9 + 9,= 1.

Строим график $2 y = x9 + 29x+ 19,при x ≥ − 1$ по точкам $(− 1,0)$ и $(2,1).$

Строим график $√ --- y = − 3 − x+ 1$ по точкам $(0,1)$ и $(− 1,− 2).$

Получаем картинку:

$PIC$

Графики функций вне пределов II четверти изображены пунктиром — эти части графиков не входят в ОДЗ.

Рассмотрим третье уравнение системы. $y = x+ a$ — уравнение прямой с угловым коэффициентом $k = 1,$ которая двигается вверх-вниз в зависимости от значения параметра.

Резюмируем анализ всех трёх уравнений системы: единственное решение она имеет только тогда, когда все три графика пересекаются в одной точке — точке пересечения графика параболы и графика функции арифметического корня.

Заметим, что графики параболы и арифметического корня симметричны относительно прямой $y = − x.$ Это легко установить, рассмотрев координаты четырёх отмеченных на рисунке точек:

(− 1,0) и (0,1),

(2,1) и (− 1,− 2).

Таким образом, поскольку на ОДЗ функции монотонны, то пересекаются эти два графика в одной точке — точке на прямой $y = − x$ (на рисунке ниже она отмечена красным цветом).

$PIC$

Найдём координаты данной точки (корень у уравнения должен быть ровно один в силу монотонности функций):

√ --- − x = − 3 − x + 1,

√--- − x − 1 = − 3 − x.

Помним об условии для возведения в степень:

2 √ ---2 (− x− 1) = (− 3 − x),

x2 + 2x+ 1 = − 9x,

x2 + 11x+ 1 = 0,

2 √ -- 2 D = 11 − 4⋅1⋅1 = (3 13),

− 11+ 3√13 − 11− 3√13- x1 = ----------, x2 =-----------. 2 2

Проверим $x1$ на выполнение условия $x > − 1 :$

√ -- − 11-+-3-13 2 > − 1,

√ -- − 11 + 3 13 > − 2,

3√13-> 9,

117 > 81.

Следовательно, $x1$ — наш искомый корень и одновременно с этим абсцисса красной точки. Найдём её ординату:

√ -- y = − − 11-+-3-13. 2

Таким образом, координаты данной точки $√-- √-- (−11+3-13,− −-11+3-13). 2 2$

Найдём значение параметра $a,$ при котором $y = x +a,$ подставив в это уравнение точки выше:

√ -- √-- − 11 + 3 13 − 11 + 3 13 − ----2------= -----2-----+ a,

√ -- a = 11− 3 13.

Вот так выглядит рисунок при найденном значении параметра:

$PIC$

Ответ:

$a = 11− 3√13-$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованные переходы	3

Верно наложено условие существования одного решения, но по ходу исследования допущена ошибка	2

Выполнен равносильный переход к квадратному уравнению с учетом всех ограничений	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 3#72214

Найдите все значения параметра $a,$ при каждом из которых уравнение $√x-−-2a-⋅cosx = √x-−-2a⋅sinx$ имеет ровно один корень на отрезке $[0;π].$

Показать ответ и решение

Запишем ограничения, определяющие ОДЗ уравнения:

x− 2a ≥ 0,

x ≥ 2a.

Найдём корни уравнения:

√------ √------ x − 2a⋅cosx = x − 2a⋅sin x,

√x-−-2a-⋅cosx − √x-−-2a⋅sinx = 0,

√------ x − 2a⋅(cosx− sin x) = 0,

$[ √ ------ x− 2a = 0, cos x− sin x = 0.$

Во второй строке совокупности записано однородное тригонометрическое уравнение первой степени $cosx− sin x = 0$ . Если хотя бы одно слагаемое равно 0, то нулю равно и другое, и мы получаем противоречие с ОТТ.

Следовательно, ни синус, ни косинус не равны 0 и на одну из этих функций можно поделить обе части уравнения. Разделим второе уравнение на $sin x,$ а обе части первого возведём в квадрат.

$[ x− 2a = 0, ctg x− 1 = 0.$

$⌊ x = 2a, ⌈ π- x = 4 +πn, n ∈ ℤ.$

Рассмотрим уравнение $x = 2a.$ Проанализируем систему, при всех решениях которой корень лежит как на данном отрезке, так и в ОДЗ:

{ 0 ≤ 2a ≤ π, 2a ≥ 2a.

{0 ≤ a ≤ π, 2 a ∈ R.

Таким образом, корень $x = 2a$ нам подходит при $π a ∈ [0;2].$

Рассмотрим уравнение $π x = 4 + πn,n ∈ ℤ.$ Из всех корней данной серии на данный отрезок попадает только $π 4.$ Проанализируем систему, при всех решениях которой корень лежит как на данном отрезке, так и в ОДЗ:

{ π 0 ≤ 4 ≤ π, π4 ≥ 2a.

{ a ∈ R, π8 ≥ a.

Таким образом, корень $x = π4$ нам подходит при $a ∈ (− ∞; π8].$

Рассмотрим случай совпадения корней:

π 2a = -, 4

a = π. 8

Проанализируем найденные промежутки:

1. При $a ∈ (− ∞; 0)$ требованиям задачи удовлетворяет только один корень $π . 4$ Это часть ответа.

2. При $a ∈ [0; π) 8$ требованиям задачи удовлетворяют оба корня $π 4$ и $2a.$ Это не часть ответа, корней слишком много.

3. При $a = π 8$ корни $π 4$ и $2a$ совпадают и требованиям задачи удовлетворяет только один уникальный корень $π. 4$ Это часть ответа.

4. При $a ∈ (π; π] 8 2$ требованиям задачи удовлетворяет только один корень $2a.$ Это часть ответа.

5. При $a ∈ (π;+∞ ) 2$ требованиям задачи не удовлетворяет ни один корень. Это не часть ответа.

Ответ:

$[ ] a ∈ (− ∞; 0)∪ π-; π 8 2$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

С помощью верного рассуждения получены оба промежутка, входящие в ответ, с неверным включением—исключением концевых точек	3

С помощью верного рассуждения получен один промежуток, входящий в ответ	2

С помощью верного рассуждения получен один промежуток, входящий в ответ, с неверным включением—исключением концевых точек	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 4#44653

Найдите все значения параметра $a$ , при каждом из которых общая часть двух множеств: ${x :|x|≥ 1}$ и $[a − 2;a+ 2]$

а) является отрезком;

б) является объединением двух отрезков;

в) является объединением отрезка и точки;

г) является пустым множеством.

Показать ответ и решение

Первое множество представляет собой объединение двух лучей $x ≥1$ и $x≤ −1$ , второе — отрезок. Так как в пересечении луча и отрезка может получаться пустое множество, точка или отрезок, то в пересечении объединения двух лучей с отрезком может получаться любая комбинация, состаоящая из двух таких множеств. Будем располагать отрезок $[a − 2;a +2]$ относительно множества ${x :|x|≥ 1}.$ А точнее, располагать точку $a+ 2$ и смотреть, где может находиться точка $a− 2$ и какие из этих положений нам подходят для каждого конкретного случая. Всего существует 5 различных мест, где можно расположить точку относительно отрезка ${x :|x|≥ 1}:$

I: левее точки $− 1;$

II: в точке $− 1;$

III: между точками $− 1$ и $1;$

IV: в точке $1;$

V: правее точки $1.$

а)

I,II.

Тогда мы в любом случае будем получить отрезок, так как точка $a− 2$ находится всегда левее точки $a+ 2,$ следовательно, и левее точки $− 1.$

$]−[[a] 1− a1+22$

Значит,

a+ 2≤ − 1 ⇔ a≤ −3

III.

Тогда, чтобы в пересечении получить отрезок, точка $a− 2$ должна располагаться в I месте. В противном случае мы получим либо точку (если $a− 2$ располагается во II месте), либо пустое множество (если $a− 2$ в III).

$]−[[a] 1− a1+22$

Значит,

( { −1 <a + 2< 1 ( ⇔ −3 < a< −1 a− 2< − 1

Заметим, что достаточно было наложить условие на точку $a+ 2,$ так как расстояние между точками $a − 2$ и $a+ 2$ равно $4,$ а между точками $− 1$ и $1$ равно $2,$ следовательно, если точка $a+ 2$ находится в III месте, то точка $a− 2$ автоматически может находиться только в I месте.

IV.

Тогда в любом случае мы будем получать либо отрезок и точку (если $a− 2$ находится в I месте), либо две точки (если $a− 2$ находмтся во II месте), либо одну точку (если $a− 2$ находится в III месте). Ни один из получаемых случаев нам не подходит.

$a]−[[a]+ 1−1=22$
или

$aa]−[[−]+ 11=22=$
или

$a]−[[a]+ 1−1=22$

V.

Тогда мы получаем отрезок, если точка $a− 2$ находится в IV или V местах.

$]−[[a] 1− a1+22$

Заметим, что достаточно поставить условие на точку $a− 2,$ так как точка $a +2$ в любом случае находится правее точки $a− 2.$ Значит,

a − 2 ≥ 1 ⇔ a≥ 3

Итоговые $a ∈(−∞; −1)∪ [3;+∞ ).$

б)

I,II,III,IV.

Не подходят (следует из пункта а)).

V.

Тогда I место — единственный вариант расположения для $a− 2$ .

$]−[[a]a 1−+122$

Значит,

({ a+ 2 >1 ⇔ −1 < a< 1 (a− 2 <− 1

Итоговые $a ∈(−1;1).$

в)

I,II,III.

Не подходят (следует из пункта а)).

IV.

Повторим подходящую картинку ( $a− 2$ находится в I месте)

$a]−[[a]+ 1−1=22$

Значит,

( { a+ 2= 1 ⇔ a= −1 ( a− 2< −1

V.

Тогда $a− 2$ должна совпадать с $− 1,$ то есть находиться во II месте.

$a]−[[−]a 1+12=2$

Значит,

( {a + 2> 1 ⇔ a = 1 (a − 2= −1

Следоватекльно, итоговые $a∈ {−1;1}.$

г) Пустое множество мы получим, если отрезок не будет иметь пересечений с лучами, следовательно, целиком будет содержаться в отрезке $[−1;1].$ Это невозможно по рассуждениям из пункта а): расстояние между точками $a− 2$ и $a +2$ равно $4,$ а между точками $− 1$ и $1$ равно $2,$ а отрезок большей длины не может целиком содержаться в отрезке меньшей длины.

Также это можно было бы понять из системы

( {a +2 < 1 ( ⇔ a ∈∅ a − 2 > −1

Ответ:

а) $a ∈(− ∞;−1)∪ [3;+ ∞)$

б) $a∈ (−1;1)$

в) $a∈ {−1;1}$

г) $a∈ ∅$

Ошибка.
Попробуйте повторить позже

Задача 5#44643

Найдите все значения параметра $a$ , при каждом из которых уравнения

x2+ ax+ 2012= 0 и x2 +2012x+ a= 0

имеют хотя бы один общий корень.

Показать ответ и решение

Если два уравнения имеют общие решения, то система из этих уравнений также имеет решения. Найдем те $a$ , при которых система

({ 2 x + ax + 2012 =0 ( x2+ 2012x+ a =0

имеет решения. Будем рассматривать эту систему как обычную систему из двух уравнений с двумя неизвестными. Выразим $a$ из второго равенства и подставим в первое:

({ x2+ ax+ 2012 = 0 ⇔ ( a= −x2 − 2012x ({ 2 2 x + x(− x − 2012x)+ 2012= 0 ⇔ ( a= −x2 − 2012x ( { −x3− 2011x2+2012= 0 ( a= −x2 − 2012x

Заметим, что $x = 1$ является решением первого уравнения. Следовательно, это уравнение можно преобразовать следующим образом:

(x− 1)(x2+ 2012x+ 2012) =0 ⇔ ⌊ ⌈ x= 1 x2+ 2012x = −2012 ⇔ ⌊ x= 1 || |⌈ x= x1 x= x2

где $x1, x2$ — корни уравнения $x2+ 2012x= −2012$ (его дискриминант $D = 20122− 4⋅2012 > 0$ ) Следовательно, $x21+ 2012x1 = −2012,$ $x22+ 2012x2 = − 2012.$

Следовательно,

⌊({ || x= 1 ||(( a= − 12 − 2012⋅1 =− 2013 ||{ x= x1 |||( 2 ||( a= − x1− 2012x1 = 2012 ||{ x= x2 ⌈( 2 a= − x2− 2012x2 = 2012

Следовательно, $a= − 2013;2012.$

Ответ:

$a ∈{− 2013;2012}$

Ошибка.
Попробуйте повторить позже

Задача 6#36431

При каком целом $a$ уравнения $2x2+ (3a − 1)x− 3= 0$ и $6x2− (2a − 3)x− 1= 0$ имеют общий корень?

Показать ответ и решение

Заметим, что если уравнения имеют хотя бы один общий корень, то система из этих уравнений имеет хотя бы одно решение $(x;a)$ , причем найденный $x$ — это и есть общий корень двух уравнений при найденном $a$ . Решим систему из двух уравнений удобным нам способом.

({ 2 2x +(3a− 1)x− 3= 0 ( 6x2− (2a− 3)x− 1= 0

Выразим из обоих равенств $6xa$ . Получим уравнение

1 9 22x2+ 7x− 9= 0 ⇔ x1 = 2;x2 = −11

Следовательно, им соответствуют $a1 = 2;a2 =− 3949$ .

Ответ:

$a =2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#36430

Найдите все $a$ , при которых неравенство

x-− 2a−-1 x− a < 0

выполнено для всех $x∈ [1;2].$

Показать ответ и решение

Нули числителя и знаменателя $x= a$ и $x= 2a+ 1$ . Они неоднозначно располагаются на числовой прямой. Но если ${x ,x} ={a,2a +1} 1 2$ , то решением неравенства будет $x ∈(x1;x2)$ , где $x1 <x2$ . Тогда, чтобы выполнялось условие задачи, нужно, чтобы

⌊ ⌈a< 1< 2< 2a+ 1 2a+ 1< 1< 2< a

Решим первое неравенство:

a< 1< 2< 2a+1 ({ a< 1 ( (2< 2a +1 { a< 1 ( 0,5< a 0,5< a< 1

Решим второе неравенство:

2a+1 <1 <2 <a ({ 2a +1< 1 ( 2< a ({a <0 ( 2 <a

Такая система не имеет решений. Значит,

⌊ ⌈a< 1< 2< 2a+ 1 2a+ 1< 1< 2< a ⇒ 0,5< a< 1

Таким образом, ответ: $a∈ (0,5;1).$

Ответ:

$a ∈(0,5;1)$

Ошибка.
Попробуйте повторить позже

Задача 8#36428

Найти все значения параметра $a$ , при каждом из которых из неравенства

2 x +a ≤0

следует неравенство

(x+ 2a)⋅√3-− x≤ 0

Показать ответ и решение

Первое решение.

Поймём, что данное следствие реализуется, если множество решений первого неравенства полностью содержится в множестве решений второго. Посмотрим, как выглядят эти множества решений.

Решим второе неравенство

√---- (x+ 2a)⋅ 3 − x≤ 0

⌊ 3 − x =0 || ( |⌈ { 3− x> 0 ( x+ 2a ≤0

⌊ x =3 ||| ({ ⌈ x< 3 ( x≤ −2a

x ∈{3}∪(−∞, min(3,−2a)]

Теперь рассмотрим решение первого неравенства в зависимости от $a$

x2 ≤− a

При $a> 0: x∈ ∅.$ Видно, что

∅ ∈{3}∪(−∞, −2a]

Значит, $a> 0$ подходят.

При $a= 0: x= 0.$ Видно, что

{0}∈ {3} ∪(−∞,0]

Значит, $a= 0$ подходит.

При $[ √---√--] a< 0: x∈ − −a, −a .$ Посмотрим как должны располагаться множества на числовой прямой

$PIC$

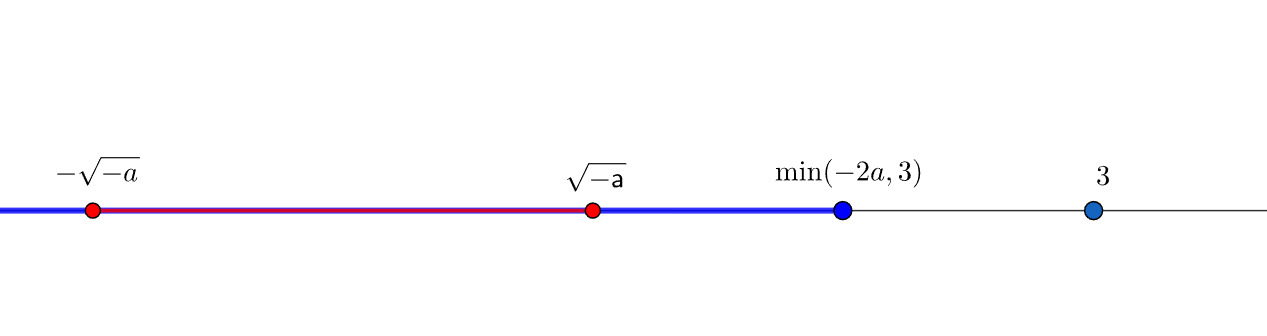
Из этого понимаем, что нужные $a$ будут удовлетворять условию

√ --- −a≤ min(3,−2a)

( { √−a-≤3 ( √--- −a ≤− 2a

Решаем систему с учётом, что $a< 0,$ получаем

({ a ≥− 9 1 ( a ≤− 4

В итоге, объединив все случаи, получаем $a∈ [−9,−0,25]∪[0,+ ∞).$ _____________________________________________

Второе решение.

Введем плоскость $xOa$ . В ней решением неравенства при конкретном $a$ будет пересечение прямой $a= a0$ с областью, которая задается неравенством. То, что одно уравнение является следствием другого, означает, что пересечение прямой $a =a0$ с множеством, задаваемым вторым неравенством, будет полностью содержать в себе пересечение прямой $a =a0$ с множеством, задаваемым первым неравенством.

Неравенство $2 x + a≤ 0$ задает область "под параболой" $2 a =− x$ .

Неравенство $√ ---- (x+ 2a) 3− x ≤0$ представим в виде равносильной совокупности:

⌊ |( 3− x= 0 ||⌈{ 3− x >0 ( x+ 2a ≤0

Эта система на плоскости представляет собой вертикальную прямую $x= 3$ и область, лежащую "ниже"прямой $a= − x2$ и "левее"c $x = 3:$

$PIC$

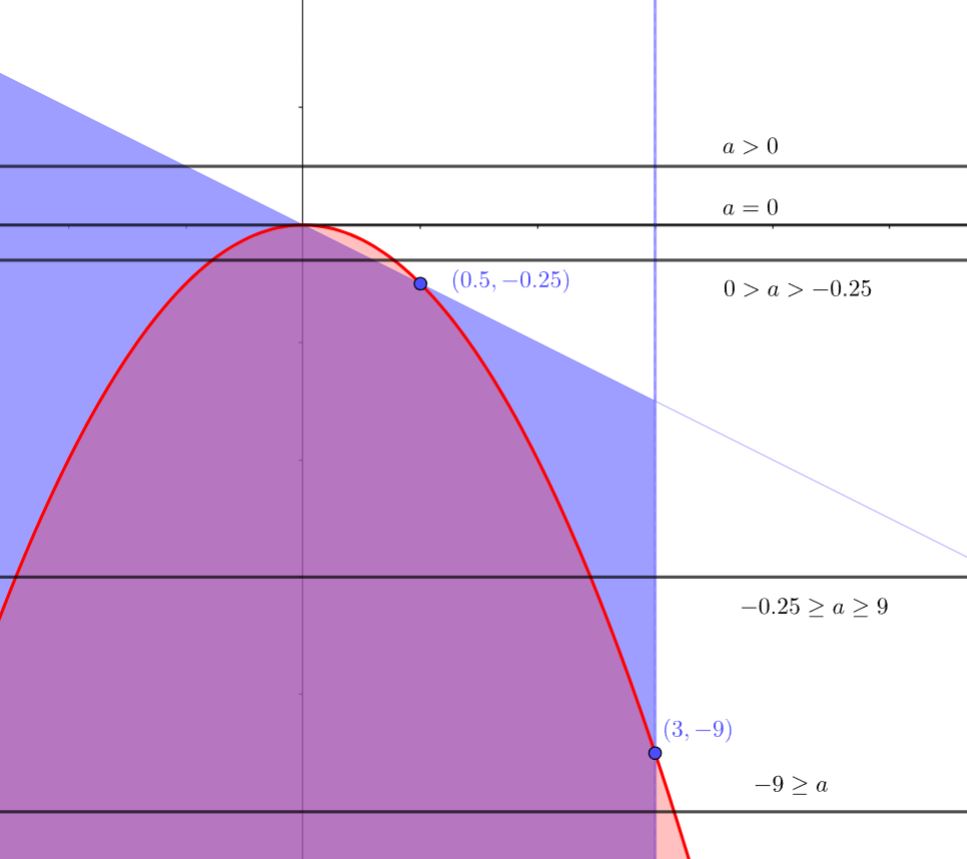
Теперь проанализируем решения неравенств при каждом $a$ .

1 случай.) $a> 0$ .

При таких значениях $a$ первое неравенство не имеет решений. Значит, любое другое неравенство будет его следствием.

2 случай.) $a= 0$ .

Решением первого неравенство будет ${0}$ , а решением второго $(−∞;0]$ . Т.е. второе неравенство является следствием первого.

3 случай.) $0> a> −0.25$ .

Как мы видим из рисунка, существуют точки "внутри"параболы, которые не принадлежат области второго неравенства. Т.е. второе неравенство не будет следствием первого.

4 случай.) $− 0.25≥ a≥ −9$ .

При таких значениях $a$ все решения первого неравенство лежат внутри множества решений второго. Т.е. второе неравенство —- следствие первого.

5 случай.) $− 9> a$ .

При таких значеиях $a$ среди решений первого неравенства есть решения $> 3$ . Но у второго неравенства таких решений быть не может. Т.е. второе неравенство не является следствием первого.

Итого получаем $a∈ [− 9;−0.25]∪[0;+ ∞)$

Ответ:

$[−9;− 0,25]∪[0;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 9#36424

Найдите все значения $a$ , при которых уравнения

2 2 (2a − 1)x +6ax+ 1= 0 и ax − x +1 =0

имеют общий корень.

Показать ответ и решение

Заметим, что если уравнения имеют хотя бы один общий корень, то система из этих уравнений имеет хотя бы одно решение $(x;a)$ , причем при найденный $x$ – это и есть общий корень двух уравнений при найденном $a$ . Решим систему из двух уравнений удобным нам способом.

({ 2 (2a− 1)x + 6ax +1 =0 (ax2− x+ 1= 0

Выразим из обоих равенств $a$ , заметим, что при этом нужно будет делить на $x2$ , что не является нулем второго уравнения. Получим уравнение

2 3 2 2xx2−+61x-= x−x21 ⇔ (x-− 1x)2((x2x−2+x6x−)-6x)-=0

Корнями данного уравнения будут $x1 = 1;x2 =− 2;x3 = 3$ , следовательно, $a1 =0;a2 = − 34;a3 = 29$ .

Ответ:

$a =− 0,75; 0; 2 9$

Ошибка.
Попробуйте повторить позже

Задача 10#2641

При каких $a$ все решения неравенства $x − 4 + 2a < 0$ являются решениями неравенства $2x + 3 − a < 0$ ?

Показать ответ и решение

Из условия следует, что множество решений первого неравенства должно содержаться во множестве решений второго неравенства. Решим оба неравенства: $x < 4 − 2a$ и $x < a−23$ . Чтобы луч $(− ∞; 4 − 2a)$ содержался в луче $(− ∞; a−3) 2$ , нужно, чтобы

a − 3 11 4 − 2a ≤ --2--- ⇒ a ≥ -5-

Ответ:

$a ≥ 151$

Ошибка.
Попробуйте повторить позже

Задача 11#2640

Найдите все $a$ , при которых совпадают множества решений уравнений $(a2 + a − 6)x = 2a2 − 3a − 2$ и $(3a2 − a − 10)x = 3a2 − 4a − 4$ .

Показать ответ и решение

Заметим, что оба уравнения линейного типа. Их можно переписать в виде:
$(a + 3)(a − 2)x = (a − 2)(2a + 1)$ ;
$(3a + 5)(a − 2)x = (a − 2)(3a + 2)$ .

Рассмотрим по отдельности случаи, когда коэффициент при $x$ равен нулю и когда он не равен нулю:

1) $a = 2$ . Тогда оба уравнения примут вид $0 = 0$ , и решениями каждого будут $x ∈ ℝ$ . Следовательно, множества их решений совпадают.

2) $a = − 3$ . Тогда первое уравнение не имеет решений, так как левая часть равна нулю, а правая – нет; второе уравнение имеет корень. Следовательно, их множества решений не совпадают.

3) $5 a = − 3$ . Аналогично пункту 2.

4) $a ⁄= − 3;− 5;2 3$ .
Тогда корень первого уравнения $x = 2a+1 a+3$ ; корень второго $x = 3a+2- 3a+5$ . Чтобы множества решений уравнений совпали, нужно, чтобы совпали данные корни:

2a + 1 3a + 2 1 -------= ------- ⇒ a = − 1;-- a + 3 3a + 5 3

Оба найденных числа удовлетворяют условию $a ⁄= − 3;− 5;2 3$ .

Ответ:

$a = − 1; 13;2$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#1958

При каких значениях параметра $a$ неравенства

|x − 2| < 3 и x2 − (a − 1)x − a < 0

равносильны.

Показать ответ и решение

Для того, чтобы два неравенства были равносильны, нужно, чтобы они имели одинаковые решения.

Решим первое неравенство:

{ x − 2 < 3 |x − 2| < 3 ⇔ x − 2 > − 3 ⇔ − 1 < x < 5

Значит, $x ∈ (− 1;5)$ должно являться решением второго неравенства. Это значит, что дискриминант уравнения $x2 − (a − 1)x − a = 0$ должен быть больше нуля и числа $− 1$ и $5$ должны являться его корнями:

(| (a − 1)2 + 4a > 0 { (− 1)2 − (a − 1) ⋅ (− 1) − a = 0 ⇔ a = 5 |( 52 − 5(a − 1) − a = 0

Ответ:

$a ∈ {5}$

Ошибка.
Попробуйте повторить позже

Задача 13#1305

При каких $a$ множества решений уравнения $(2a2 − a − 1)x = 5a − 5$ и неравенства $(6a2 + a − 1)x ≥ 3a + 2$ совпадают?

Показать ответ и решение

Мы имеем уравнение и неравенство линейного типа.

Для данного уравнения при $2a2 − a − 1 = 0$ решениями будут либо $x ∈ ∅$ , либо $x ∈ ℝ$ (нужно проверить), при $2 2a − a − 1 ⁄= 0$ решением будет одна точка (а именно, $-5a−5-- x = 2a2− a−1$ ).

Для данного неравенства при $6a2 + a − 1 = 0$ решениями будут либо $x ∈ ∅$ , либо $x ∈ ℝ$ (нужно проверить), при $6a2 + a − 1 ⁄= 0$ решением будет некоторый луч (либо от $− ∞$ до числа, либо от числа до $+ ∞$ ).

Итак, мы разобрали типы ответов, которые мы можем получить, решая уравнение и неравенство. Таким образом, единственная ситуация, когда решение уравнения и решение неравенства могут совпасть, это если решениями будут $x ∈ ∅$ либо $x ∈ ℝ$ , то есть как минимум при $2a2 − a − 1 = 0$ и $6a2 + a − 1 = 0$ .

Решением уравнения $2 2a − a − 1 = 0$ будут $a = − 0,5;1$ , решением уравнения $2 6a + a − 1 = 0$ будут $a = − 0,5; 13$ . Следовательно, одновременное выполнение этих двух условий возможно при $a = − 0,5$ .

При $a = − 0,5$ уравнение примет вид $0 ⋅ x = − 7,5$ (решениями этого уравнения будут $x ∈ ∅$ ), неравенство примет вид $0 ⋅ x ≥ 0,5$ (это неравенство также не имеет решений, то есть $x ∈ ∅$ ). Следовательно, действительно, при $a = − 0,5$ решения уравнения и неравенства совпадают.

Ответ:

$a = − 0,5$

Ошибка.
Попробуйте повторить позже

Задача 14#668

При каких значениях параметра $a$ неравенства

|x − 1| ≥ 2 и x2 − ax − a ≥ 1

равносильны.

Показать ответ и решение

Для того, чтобы два неравенства были равносильны, нужно, чтобы они имели одинаковые решения.

Решим первое неравенство:

[ x − 1 ≥ 2 |x − 1| ≥ 2 ⇔ x − 1 ≤ − 2 ⇔ x ∈ (− ∞; − 1] ∪ [3;+∞ )

Значит, $x ∈ (− ∞; − 1] ∪ [3;+ ∞ )$ должно являться решением второго неравенства. Это значит, что дискриминант уравнения $x2 − ax − a − 1 = 0$ должен быть больше нуля и числа $− 1$ и $3$ должны являться его корнями:

(| a2 + 4(a + 1) > 0 { (− 1)2 + a − a − 1 = 0 ⇔ a = 2 |( 32 − 3a − a − 1 = 0

Ответ:

$a ∈ {2}$

Ошибка.
Попробуйте повторить позже

Задача 15#667

При каких значениях параметра $a$ уравнения

x3 + ax + 1 = 0 и x4 + ax2 + 1 = 0

имеют хотя бы один общий корень.

Показать ответ и решение

Пусть $x0$ — общий корень данных уравнений. Заметим, что $x0 ⁄= 0$ (т.к. $03 + a ⋅ 0 + 1 ⁄= 0$ ). Тогда верна следующая система:

{ 3 x0 + ax0 + 1 = 0 x40 + ax20 + 1 = 0

Умножим первое уравнение системы на $x0$ (имеем право, т.к. $x0 ⁄= 0$ ) и вычтем из полученного уравнения второе уравнение системы:

{ { { x40 + ax20 + x0 − (x40 + ax20 + 1) = 0 x0 = 1 x0 = 1 x4+ ax2+ 1 = 0 ⇒ x4 + ax2 + 1 = 0 ⇒ a = − 2 0 0 0 0

Таким образом, данные уравнения общим корнем могут иметь только $x0 = 1$ , и для того, чтобы $x0 = 1$ являлся их общим корнем, необходимо, чтобы $a = − 2$ . Проверкой можно убедиться, что $x0 = 1$ и $a = − 2$ подходят в оба уравнения.

Ответ:

$a ∈ {− 2}$

Ошибка.
Попробуйте повторить позже

Задача 16#575

При каких $a$ множество решений неравенства

2 (a − 3a+ 2)x− a+ 2≥ 0

содержит полуинтервал $[2;3)?$

Показать ответ и решение

Преобразуем неравенство к виду

(a− 1)(a− 2)x≥ a− 2

Получили линейное неравенство. Рассмотрим случаи.

1) $a= 2.$

Тогда неравенство примет вид $0 ≥ 0,$ что верно при любых значениях $x,$ следовательно, множество решений содержит полуинтервал $[2;3).$

2) $a= 1.$

Тогда неравенство примет вид $0 ≥ −1,$ что верно при любых значениях $x,$ следовательно, множество решений содержит полуинтервал $[2;3).$

3) $(a− 1)(a− 2)> 0 ⇔ a ∈(−∞; 1)∪(2;+∞ ).$

Тогда неравенство примет вид

x≥ -1-- a− 1

$PIC$

Для того, чтобы множество решений содержало полуинтервал $[2;3),$ необходимо

1 3− 2a a−-1 ≤2 ⇔ a-− 1-≤ 0 a ∈ (− ∞;1)∪ [1,5;+ ∞ )

Учитывая условие $a ∈ (− ∞;1)∪ (2;+∞ ),$ получаем

a ∈(−∞; 1)∪(2;+∞ )

4) $(a− 1)(a− 2)< 0 ⇔ a ∈(1;2).$

Тогда неравенство примет вид

-1-- x≤ a− 1

$PIC$

Для того, чтобы множество решений содержало полуинтервал $[2;3),$ необходимо

-1-- ≥3 ⇔ 3a−-4≤ 0 a− 1 ( a] − 1 a∈ 1; 4 3

Учитывая условие $a ∈ (1;2),$ получаем

( ] a∈ 1; 4 3

Объединяя все случаи, получаем

( 4] a∈ −∞; 3 ∪[2;+ ∞)

Ответ:

$( 4] a ∈ −∞; 3 ∪ [2;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Ответ отличается от верного невключением одного из значений $a = 43$ или $a= 2$	3

Верно рассмотрен хотя бы один из случаев $(a− 1)(a − 2)> 0∕$ $(a− 1)(a− 2)< 0$	2
ИЛИ
Рассмотрены оба случая, но есть ошибка при решение неравенства, задающего условие содержания полуинтервала в решении

Верно рассмотрен случай $(a− 1)(a− 2)= 0$	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Комментарий

Если в решении не был рассмотрен случай $(a− 1)(a− 2) = 0,$ то оно оценивается не более, чем в 2 балла.

Предыдущий раздел

Следующий раздел