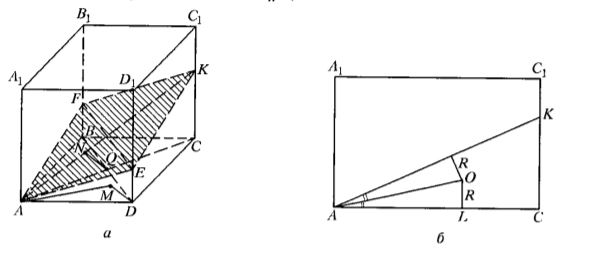
Плоскость пересечет грань куба по прямой где ребро в некоторой точке (см. рис. ). Пусть - середина и основания перпендикуляров, опущенных соответственно из точек и на плоскость Тогда так как и По условию откуда находим Из треугольника в котором находим и поэтому Пусть - площадь сечения куба плоскостью тогда где и поэтому

Найдем радиус вписанного шара. Заметим, что центр О шара лежит на биссектрисе угла , а проекция точки на грань принадлежат Из треугольника в котором находим где Так как тo

Замечание. Искомый радиус можно найти, заметив что он равен радиусу шара, вписанного в треугольную пирамиду где точка пересечения прямых и точка пересечения прямых и используя формулу где - объем пирамиды ее полная поверхность.