Ошибка.
Попробуйте повторить позже
Последовательность ( ) удовлетворяет условиям
Какие значения может принимать ?
Источники:
Подсказка 1
Давайте для начала возведём в квадрат и посмотрим, что же у нас получается после приведения подобных. Во-первых, у нас получается симметричное уравнение относительно a_(n + 1) и a_n. А это значит, что то, что верно для a_(n - 1) верно и для a_(n + 1) относительно a_n. Что можно тогда заметить?
Подсказка 2
Мы можем заметить, что уравнению t^2 - (2a_n + 1)*t + a^2_n - a_n = 0 удовлетворяют и а_(n - 1), и a_(n + 1). Значит, по теореме Виета, a_(n - 1) + a_(n + 1) = 2a_n + 1. Теперь попробуйте найти первые несколько членов!
Подсказка 3
У нас получается такая прогрессия - 1,3,6,10….- это же значения суммы первых n натуральных чисел. Попробуйте это доказать, и тогда задача сведётся к тому, чтобы записать ответ.
Выписав условие , возведем равенство в квадрат и запишем его для двух соседних членов последовательности
То есть получаем, что и
— два корня уравнения
По теореме Виета получаем
Первые члены последовательности равны Это очень похоже на суммы первых
натуральных чисел. Давайте по индукции
докажем формулу:
База очевидна:
Переход ясен:
Поэтому
Ошибка.
Попробуйте повторить позже
Функция , определённая на действительных числах, принимает действительные значения. Известно, что для любых действительных
и
выполнено равенство
. Найдите все такие функции
.
Источники:
Подсказка 1
Давайте подумаем. Обычно мы хотим, когда видим функциональные уравнения, подставить что-то удобное вместо y. Что здесь можно такое подставить, чтобы у нас получилось удобное уравнение? В каком бы виде мы бы хотели видеть это уравнение?
Подсказка 2
Если подставить y = 4x, то слева и справа будет f(x). Тогда мы сможем разбить наше уравнение на совокупность двух простых. Что либо f(x) = 0, либо f(4x) = 1. Значит ли это, что мы решили задачу?
Подсказка 3
А вот и нет! Ведь если у нас для любого x верно, что либо f(x) = 1, либо f(x) = 0, то не значит, что у нас возможны только такие функции. Это значит лишь то, что множество значений f равно 0 и 1. Поэтому для полного решения требуется доказать, что если f(x) = 0 в какой-то точке, то f(x) = 0 тождественно. Тогда переход, о котором говорилось выше, корректен.
Если при каком-то выполняется
то для любого
верно
поэтому для любого
выполняется
Если же для любого значения
, то для любого
должно быть выполнено
где после сокращения на получаем
Таких функции две: константа 0 и константа 1. ()
Ошибка.
Попробуйте повторить позже
Ортогональной проекцией правильной треугольной пирамиды на некоторую плоскость является параллелограмм с острым углом .
Найдите объём пирамиды, если площадь её боковой поверхности равна 54.
Источники:
Подсказка 1
Чтобы нормально работать с картинкой, рассмотрим две пары скрещивающихся рёбер пирамиды (например, AB, CD, BC, AD). Ведь их достаточно для построения проекции. Пирамида правильная, значит, на этих рёбрах удобно отметить их середины (например, точки M, N, Q, P соответственно). Ведь отрезки MN и PQ являются перпендикулярами к этим рёбрам. Но, кажется, этого мало, ведь надо понять, какие свойства имеют их проекции. Попробуйте выяснить, как связаны эти отрезки и их проекции, основываясь на том, что ортогональная проекция пирамиды - параллелограмм.
Подсказка 2
В силу того, что проекцией пирамиды является параллелограмм, эти отрезки параллельны плоскости проекции. Тогда проекции MN и PQ параллельны самим отрезкам, равны им и перпендикулярны сторонам ромба. Также, так как пирамида правильная, MN и PQ равны, а значит, и их проекции тоже. Что тогда мы можем сказать про этот параллелограмм?
Подсказка 3
Верно! Это же ромб! Ведь в нём высоты, проведённые к смежным сторонам, равны. Тогда, если введём угол между ребром основания пирамиды и плоскостью проекции и длину стороны основания и боковой стороны трапеции (например, через a и b), то сможем выразить стороны ромба через a, b и этот угол и получить уравнение, ведь эти стороны равны.
Подсказка 4
Теперь мы получили, что тангенс угла между ребром основания пирамиды и плоскостью проекции равен a/b. Отлично! Мы можем выразить и синус, и косинус этого угла через a/b, а значит, и сторону ромба мы можем выразить через a и b (для удобства можно заменить a/b на новую переменную). Но мы ещё никак не воспользовались тем условием, что угол ромба равен 60 градусам. Это нужно исправить, например, записав уравнение на синус этого угла, выразив его как отношение высоты ромба на его сторону. Если мы ещё и выразим высоту через a и b, то получится записать уравнение на a и b.
Подсказка 5
Мы ведь знаем, что проекция MN - это высота ромба. Тогда так как проекция равна MN, то и высота равна этому отрезку. А вот его уже легче искать. Это можно сделать, выразив площадь треугольника MDC двумя способами.
Подсказка 6
Подставив MN в уравнение, мы получили, что (a/b)^2 = 2. Осталось воспользоваться последним условием задачи про площадь боковой поверхности. Выразив её через a и b, мы получаем уравнение, через которое находим a и b. Дело за малым, осталось лишь посчитать объём. И победа!
Пусть сторона основания пирамиды с вершиной
равна
, а боковое ребро равно
. Для построения проекции достаточно
рассмотреть две пары скрещивающихся ребер, например,
и
, проекции которых являются сторонами параллелограмма
![]()
Пусть — общий перпендикуляр пары рёбер
и
, а
— общий перпендикуляр скрещивающихся рёбер
и
.
Плоскость проекции
параллельна как
, так и
, поскольку ортогональной проекцией пирамиды является параллелограмм.
Отрезки
и
проектируются на плоскость
без изменения длины в высоты параллелограмма
и
, так как
и
обе перпендикулярны
и будут параллельны друг другу, т.к.
— параллелограмм. То есть
не просто общий
перпендикуляр
и
, но и общий перпендикуляр двух вышеописанных плоскостей. А значит, ещё это и общий перпендикуляр для
и
Поскольку пирамида правильная, . Следовательно,
В параллелограмме высоты, проведённые к смежным сторонам, равны. Значит, параллелограмм является
ромбом.
Пусть ребро наклонено к плоскости
под углом
, тогда ребро
, которое перпендикулярно
, наклонено под углом
Отсюда
![]()
Обозначим . Тогда
.
Найдём расстояние между скрещивающимися рёбрами правильной треугольной пирамиды как высоту сечения :
откуда
Тогда синус острого угла пирамиды равен . Подставляя найденные выражения и данное в условии значение
, получим
, откуда
(что невозможно) или
Площадь боковой поверхности пирамиды равна
Подставив и
, найдём
Объём правильной пирамиды равен
Ошибка.
Попробуйте повторить позже
Наименьшее значение функции
для неотрицательных , сумма которых равна
, равно
. При каком значении параметра
такое
возможно?
Источники:
Подсказка 1
Давайте внимательнее посмотрим на задачу и попробуем вспомнить хитрый способ решения неравенств, нахождения минимума или максимума. Напоминают ли вам что-то квадратные корни из суммы квадратов? Где вы такое могли видеть?
Подсказка 2
Давайте ещё подумаем, чтобы не сразу раскрывать вам все "секреты". Могли ли вы встречать подобное в геометрии? Может быть это длина какого-то отрезка?
Подсказка 3
Верно, это же теорема Пифагора, где числа под корнями являются катетами прямоугольного треугольника. Как же теперь можно проиллюстрировать нашу задачу?
Подсказка 4
Да, получается мы можем расположить отрезки с иксами вдоль одной прямой, а с числами вдоль перпендикулярной ей. В итоге, у нас получится ломанная. Понятно, что минимумом будет просто расстояние между крайними точками ломанной, а это гипотенуза с катетами из суммы наших катетов. Осталось понять, что мы знаем обе суммы и из условия про минимум найти k, решив уравнение. Победа!
На оси абсцисс отметим отрезки, равные по длине , а на оси ординат — отрезки длины
. Тогда
выражение
— это расстояние от точки
до точки
, а
— расстояние от точки
до точки
.
![]()
Таким образом, получили ломанную из точки до точки с координатами
. Ее длина не превосходит расстояния между этими точками, то есть
Тогда
Решив это уравнение, находим
Ошибка.
Попробуйте повторить позже
Решите уравнение
Источники:
Подсказка 1
В условии дано тригонометрическое уравнение с какими-то страшными аргументами тригонометрических функций, формулы тут не поприменяешь, к сожалению. В таких случаях обычно принято использовать метод оценки. Попробуйте воспользоваться им.
Подсказка 2
Давайте умножим наше уравнение на cos(3x). Что можно сказать про решения нашего уравнения, если вспомнить про ограничения на синус и на косинус?
Подсказка 3
Синус и косинус принимают значения от -1 до 1. Значит, произведение синуса на косинус будет равно 1 только в случаях, когда синус и косинус равны 1, а также когда синус и косинус равны -1 одновременно.
Подсказка 4
Рассмотрим решения cos(3x) = ±1, x = πk/3. Подставив данную серию решений в уравнение с синусом равном ±1, найдите все подходящие k.
Подсказка 5
После подстановки получается выражение 88π²*3/πk = π/2 + πn, преобразовав, получим: 3*8*11 / k = 1/2 + n. Обратите внимание, что в правой части уравнения стоит целое число с одной второй, значит, слева тоже должно быть целое число + одна вторая. Какие k подходят под данное условие?
Подсказка 6
Так как нам необходимо, чтобы получилась именно 1/2 + какое-то целое в левой части уравнение, то на место k подойдут все такие целые числа, которые при сокращении с числителем будут оставлять в знаменателе 2.
Подсказка 7
То есть, каждое k делится на какой-то набор нечетных делителей числителя и еще на 16. Получается, что все k будут четными, значит, cos(3x) может равняться только 1. Остается отобрать такие пары k и n, что sin(88π²*3/x) = 1, x = π/2 + πn.
Домножим на
Так как , равенство возможно только в случаях
Уравнение имеет решения
. Подставив эту серию в
, получаем
Тогда может принимать только следующие значения
Так как все получившиеся четны,
. Выберем из получившихся пар
такие, что
То есть те, где
четно.
или
при
или
при
или
при
или
при
Подставляя в
получаем ответ.
Ошибка.
Попробуйте повторить позже
Про действительные числа известно, что
Найдите все значения, чему может быть равно .
Источники:
Подсказка 1
Давайте посмотрим на нашу систему и попробуем найти какие-то паттерны. Заметим, что и сверху, и снизу у нас коэффициент перед членами с a и b, равен 3(или 9, когда возвели в квадрат). Да и свободный коэффициент один и тот же. Что же тогда надо сделать?
Подсказка 2
Надо вычесть второе из первого. После чего, слева мы получим c(a - 3b), а справа (3b - a)(3b + a). Значит, разложили на скобочки. Значит, либо c = 3b - a, либо а = 3b. То есть, мы выразили одну переменную через другие. Что мы обычно делаем в таком случае?
Подсказка 3
Верно, мы подставляем наше выражение вместо этой переменной и решаем уже полученную систему. Остается сделать это, понять, какой случай возможен, какой нет, и чему равно искомое ab.
Вычтем из первого уравнения второе.
В первом случае подставляем в систему и получаем
что невозможно.
Во втором случае подставляем в систему и получаем
или же
Если то
— не подходит под первое уравнение системы.
Рассмотрим любое Тогда
и
, то есть любая тройка вида
является решением системы. Искомое
выражение
может принимать любое положительное значение.
Ошибка.
Попробуйте повторить позже
Векторы , расположенные в одной плоскости с вектором
, имеют равную длину, отличную от длины вектора
. Известно,
что
Найдите
Источники:
Подсказка 1
Давайте выразим всё через a₁ и a₃, ведь именно они выделяются: a₁ = 4/9 * a₂ + 5/9 * b, a₃ = 9/16 * a₄ + 7/16 * b. Что мы можем заметить здесь? А если вспомнить словосочетание «отношение отрезков»?
Подсказка 2
Это похоже на то, что мы взяли вектора a₂ и b, провели их от одной точки и на отрезке, который соединяет их концы, поставили точку с отношение 7/9, и вот этот вектор равен a₁. Аналогично с a_3. Как теперь можно наше наблюдение совместить с фактом про равные длины из условия?
Подсказка 3
Давайте создадим треугольник AOE, где OA = a₂, OE = b. Тогда вектор a₁ понятно находится по рассуждению выше. Но ведь у нас еще есть a₃. Пусть тогда OD = a₄. Тогда, опять же, a₃ понятно ищется на картинке. Но что же все таки с равными длинами? В какой конструкции у нас много точек на одном расстоянии лежит?
Подсказка 4
Верно! Концы векторов a₁, a₂, a₃, a₄ лежат на одной окружности, при этом прямые DC, AB, OE пересекаются в одной точке и делятся понятным отношением этой самой окружностью. Что тогда остается сказать, если даны окружность и отношения секущих?
Подсказка 5
Можно сказать, что у нас EB * EA = EC * ED, если BA = 4x, а EC = 9y, то y = x/2. Осталось воспользоваться условием задачи ещё раз
Выразим и
. Поэтому
— чевиана в треугольнике
со сторонами
и
, которая
делит третью сторону
в отношении
к
. А
— чевиана треугольника
со сторонами
и
, делящая
в
отношении
к
. Так как векторы
равны, то они лежат на окружности с центром в точке
, а треугольники
и
— равнобедренные.
![]()
По теореме об отрезках секущих
Откуда
По условию , следовательно
Ошибка.
Попробуйте повторить позже
Партию новогодних шаров необходимо сложить в коробки так, чтобы в каждой коробке лежали шарики. Если использовать коробки вместимостью 100 шаров, то ровно одна коробка останется не полностью заполненной. Если взять на 11 коробок больше, но в которые помещается по 70 шаров, то вновь ровно одна коробка останется не полностью заполненной. Если же взять ещё на 5 коробок больше, но вместимостью 60 шаров, то все коробки будут полными. Сколько шаров могло быть в партии?
Источники:
Подсказка 1
Что вообще значит, что останется сколько-то коробок? Это значит, что если у нас было N коробок, то N = 100n + r_1, 0 < r_1 < 100, во втором случае - N = 70(n + 11) + r_2, а в третьем N = 60(n + 17). Подумайте, почему именно n + 17 а также, что делать с такой системой.
Подсказка 2
100n + r_1 = 70n + 770 + r_2 = 60n + 1020. Тогда, r_1 = 10k, r_2 = 10t, а значит, 4n + k = n + 77 + t = 102. Значит, n + t = 25, 4n = 102 - k. Как теперь найти n с учетом того, что все переменные должны быть больше 0?
Подсказка 3
Заметим, что 0 < k < 10, так как это кратный 10 остаток по модулю 100, но не равный 0. Значит, 4n = 102 - k > 92 => n >= 24. При этом, n = 25 - t <= 24. Победа!
Пусть — число шаров, а
— число заполненных коробок в первом случае. Тогда коробок всего
. По условию
получаем
где
Во втором случае получаем
где
И наконец, в третьем случае получаем
так как во втором случае имеем на самом деле коробок —
заполненных и одну не полностью заполненную.
Заметим, что делятся на
, то есть
где
Из получаем
Из получаем
То есть И тогда
Ошибка.
Попробуйте повторить позже
На доске написаны числа . За одну операцию Саша может выбрать два числа на доске, стереть их и записать на доску
сумму стёртых чисел. Такими операциями он хочет добиться, чтобы на доске не нашлись одно или несколько чисел, сумма
которых равна 37 (сумма одного числа — это само это число). Какое наименьшее количество операций придётся сделать
Саше?
Источники:
Подсказка 1
Нам говорят, что не должно остаться чисел, сумма которых даёт 37. При этом изначально на доске много пар чисел, которые в сумме дают 37. Какое разбиение хочется сделать первым делом?
Подсказка 2
Хочется разбить числа на пары так, чтобы в каждой паре сумма числа равнялась 37. Это сделать несложно: первое объединяем в пару с последним, второе с предпоследним и так далее. Остаётся придумать, как мы будем портить числа, то есть стирать два числа с доски и оставлять их сумму
Подсказка 3
Да, будем стирать те числа, которые дают в сумме 19, ведь тогда минимальная сумма будет ровно 38, что нас устраивает! То есть можно стирать пары чисел: 1 и 18, 2 и 17 и так далее. В таком случае сколько операций нам понадобится?
Подсказка 4
Ровно 9 операций потребуется!
Разобьем числа на пары с суммой
В каждой такой паре нужно “испортить” хотя бы одно число. За каждую операцию мы “портим” числа, то есть можем
“испортить” максимум две пары. Нужно “испортить”
пар, поэтому нужно минимум
операций. Приведем пример на
действий:
Сложим сначала с
, затем
с
и так далее до
. После проделанных действий получаем
Ряд не содержит числа , а также никакие несколько чисел не дают в сумме
, так как их сумма как минимум
Ошибка.
Попробуйте повторить позже
Все члены геометрической прогрессии положительны. Сумма первых членов прогрессии равна
а сумма обратных величин этих
членов равна
Найдите восьмой член прогрессии.
Источники:
Подсказка 1
В данной задаче самое главное и самое сложное это правильно записать то, что нам дано в условии. Давайте рассмотрим геометрическую прогрессию с первым членом b и знаменателем q. Вспомните формулу суммы первых n членов геометрической прогрессии для дальнейшего решения.
Подсказка 2
По формуле суммы геометрической прогрессии сумма первых 15 членов будет равна b*(q¹⁵ - 1) / (q - 1). Заметьте, что сумма обратных величин довольно похожа на сумму обычных, подумайте, возможно, получится ее посчитать похожим образом.
Подсказка 3
Обратные величины так же являются геометрической прогрессией, только с первым членом равным 1/b и знаменателем равным 1/q. Как тогда можно записать наше изначальное условие?
Подсказка 4
По условию мы получаем систему из двух уравнений: b*(q¹⁵ - 1) / (q - 1) = 58 и (q⁻¹⁵ - 1) / b(q⁻¹ - 1) = 14,5. Для удобства работы умножим во втором уравнении числитель и знаменатель на -q¹⁵. Вспомните, что восьмой член прогрессии равен bq⁷. Как его можно найти с помощью полученных уравнений?
Пусть — первый член прогрессии,
— знаменатель. Тогда по условию
так как все числа положительны.
Заметим сразу, что исходная прогрессия не является постоянной(то есть ), так как иначе каждый ее член был бы равен
и
тогда сумма обратных величин была бы равна
Запишем сумму первых 15 членов
Последовательность, составленная из обратных величин данной прогрессии также является геометрической прогрессией(со знаменателем
), поэтому
Преобразовав второе равенство, получаем систему
Поделив первое равенство на второе, получаем
Так как получаем значение восьмого члена прогрессии
Ошибка.
Попробуйте повторить позже
В группе из 80 человек некоторые знакомы друг с другом (знакомства взаимны). Известно, что в группе есть человек, который знает ровно 1 из оставшихся, человек, который знает ровно 2 из оставшихся, ..., человек, который знает ровно 54 из оставшихся. Докажите, что в группе есть три человека, каждые два из которых знакомы.
Источники:
Подсказка 1
Зачастую в задачах на знакомства, на какие-то дороги, где нам даны количества "соединений", удобнее всего начинать с объекта, у которого их больше всех) Попробуем рассмотреть всех знакомых человека А, у которого их 54, что можно о них сказать?
Подсказка 2
Чего же мы хотим добиться от такого множества? Найти человека B в нём, у которого с A точно есть общий знакомый. Но чтобы найти такого B, нужно хотя бы понимать, сколько у него знакомых. Но далеко не обо всех людях мы знаем количество их друзей :( Значит, попробуем сократить множество, в котором будем искать такого B. О скольких людях в множестве друзей A мы точно знаем количество знакомых?
Подсказка 3
В множестве знакомых A максимум 26 человек, у которых мы не знаем количество друзей, значит, есть как минимум 28 человек, про которых мы можем что-то сказать. Какого тогда человека мы можем "выцепить" оттуда, чтобы, наконец, найти B из подсказки 2?
Подсказка 4
Среди них есть человек B, у которого хотя бы 28 знакомых! Осталось лишь доказать, почему же у B и A обязательно есть общий знакомый из всех, при условии, что они знакомы между собой?)
Посмотрим на человека , который знает ровно 54 из оставшихся. Из них максимум 26 людей, про количество знакомых у которых в
условии ничего не сказано. Осталось как минимум 28 человек, про количество знакомых которых сказано в условии. Среди них тогда
найдётся человек
, количество знакомых которого хотя бы 28.
У , кроме
, есть ещё 53 знакомых, а у
, кроме
ещё 27 . Поскольку
, то у
и
есть хотя бы один
общий знакомый
. Тройка
и есть искомая тройка человек.
Ошибка.
Попробуйте повторить позже
Найдите все функции , для которых существует такое вещественное число
, что при всех вещественных
выполнено
равенство
Источники:
Подсказка 1
Заметим, что правая часть несимметрична относительно x и y, а левая - симметрична) Как тогда можно связать x и y?
Подсказка 2
f(x)f(y) - f(x) - 2y + a = 2f(xy+3)=f(y)f(x) - f(y) - 2x + a ⇒ f(x) - 2x = f(y) - 2y. Значит, разность f(x) - 2x постоянна! Как тогда записать f(x) и что с этим можно сделать?
Подсказка 3
f(x) = 2x + C, для некоторого действительного C и любого x) Остается лишь подставить это в равенство из условия, найти C и a)
Заметим, что
Значит, при всех выполнено
. Значит, разность
постоянна и
, для некоторого
. Подставляя в исходное равенство, получаем, что при всех
выполнено равенство:
Оно тождественно выполнено только при ; при этом
Ошибка.
Попробуйте повторить позже
В треугольнике точки
— середины сторон
а
,
— точки касания этих сторон со вписанной
окружностью соответственно. Прямые
пересекают
в точках
и
Докажите, что прямая
делит отрезок
пополам.
Источники:
Подсказка 1
Один отрезок делит другой пополам, часто это происходит потому что они являются диагоналями некоторого параллелограмма.
Подсказка 2
В данном случае окажется, CXC1Y - параллелограмм, но нужно как-то подобраться к точкам X и Y...
Подсказка 3
В этом нам поможет лемма 255, согласно ней точки X и Y лежат на биссектрисах углов A и B соответственно.
Докажем, что точки лежат на биссектрисах углов
соответственно (это утверждение известно как задача
и может быть
использовано на олимпиаде без доказательства). Так как
и
то
следовательно,
и
Аналогично
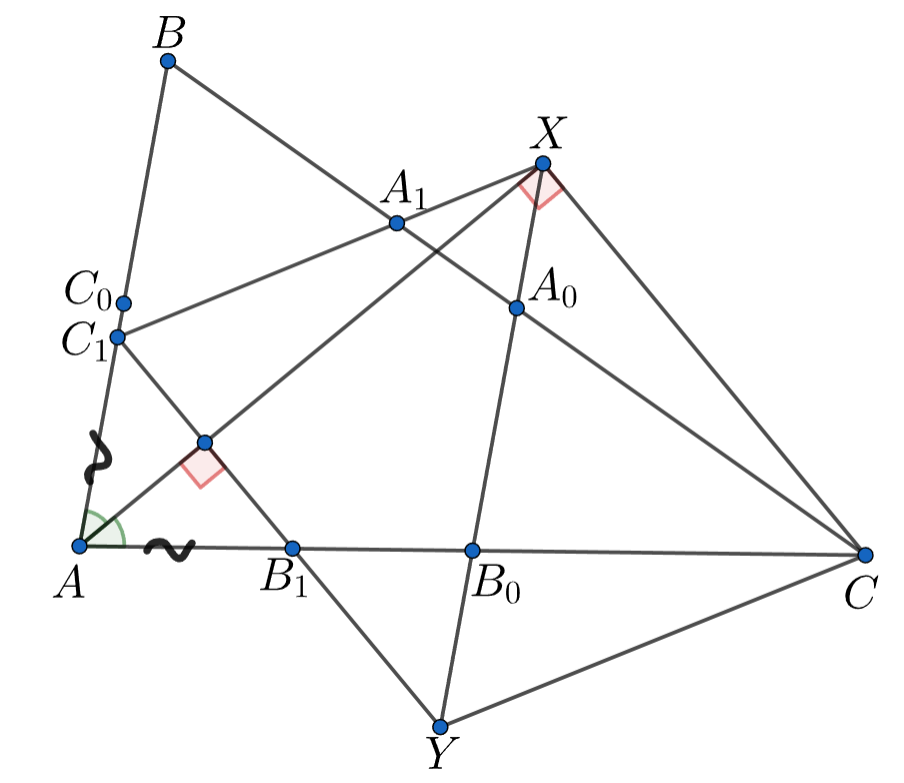
Итак, по лемме
и
потому что треугольник
равнобедренный и
в нём биссектриса,
проведённая к основанию. Следовательно,
Аналогично
Таким образом, четырёхугольник
—
параллелограмм. В таком случае его диагонали точкой пересечения делятся пополам, это даёт нам требуемое.
Ошибка.
Попробуйте повторить позже
Дано действительное число , отличное от
и
Решите уравнение
Ответ может зависеть от
Источники:
Подсказка 1
Давайте представим, что мы раскрыли скобки и избавились от знаменателей, что мы получим?
Подсказка 2
Мы получим уравнение 6-й степени! А значит, у него точно не больше 6 корней. Тогда есть соблазн попробовать угадать эти 6 корней...
Подсказка 3
Легко видеть, что t - корень. Какие замены можно попробовать сделать, чтобы найти ещё немного корней?
Подсказка 4
Левая дробь не меняется при замене x на 1-x и на 1/x, поэтому получаем новые корни, какие? Попробуйте набрать как можно больше.
Подсказка 5
Теперь лишь остаётся доказать, что при данных ограничениях на t шесть корней, которые вы нашли, всегда различные.
Докажем два утверждения:
- если
- решение уравнения, то и
также решение; действительно,
поэтому если второе равняется , то и первое - тоже.
- если
- решение уравнения, то и
также решение; действительно,
поэтому если второе равняется , то и первое - тоже.
Заметим теперь, что - точно корень исходного уравнения. Тогда, корнями являются также числа
, а тогда и
.
Можно показать, что при данных ограничениях на получившиеся 6 чисел - различны. Кроме того, исходное уравнение при
равносильно уравнению 6 -й степени, которое не может иметь больше 6 корней. Значит, найденные числа и есть все
корни.
Ошибка.
Попробуйте повторить позже
Укажите все значения параметра , при которых множество решений неравенства
для представимо в виде двух непересекающихся интервалов.
Источники:
Подсказка 1
Давайте сделаем естественную вещь в таком не очень хорошем параметре. У нас есть синус и косинус с одинаковым аргументом. Тогда попробуем сделать замену sin(t)=y и cos(t)=x. Какие условия тогда у нас будут?
Подсказка 2
Верно, тогда у нас получается система из 4 условий: основное тригонометрическое тождество, ограничение на t, ОДЗ знаменателя и само исходное неравенство. Тогда как теперь можно сформулировать вопрос задачи и найти а?
Подсказка 3
Ага, получается, что нам удовлетворяют все решения системы, где точки лежат на полуокружности и ниже, чем график y = |x− a|, который двигается вдоль оси х в зависимости от а. Осталось только определить, когда получается два непересекающихся отрезка в решении и найти из графика граничные точки для а.
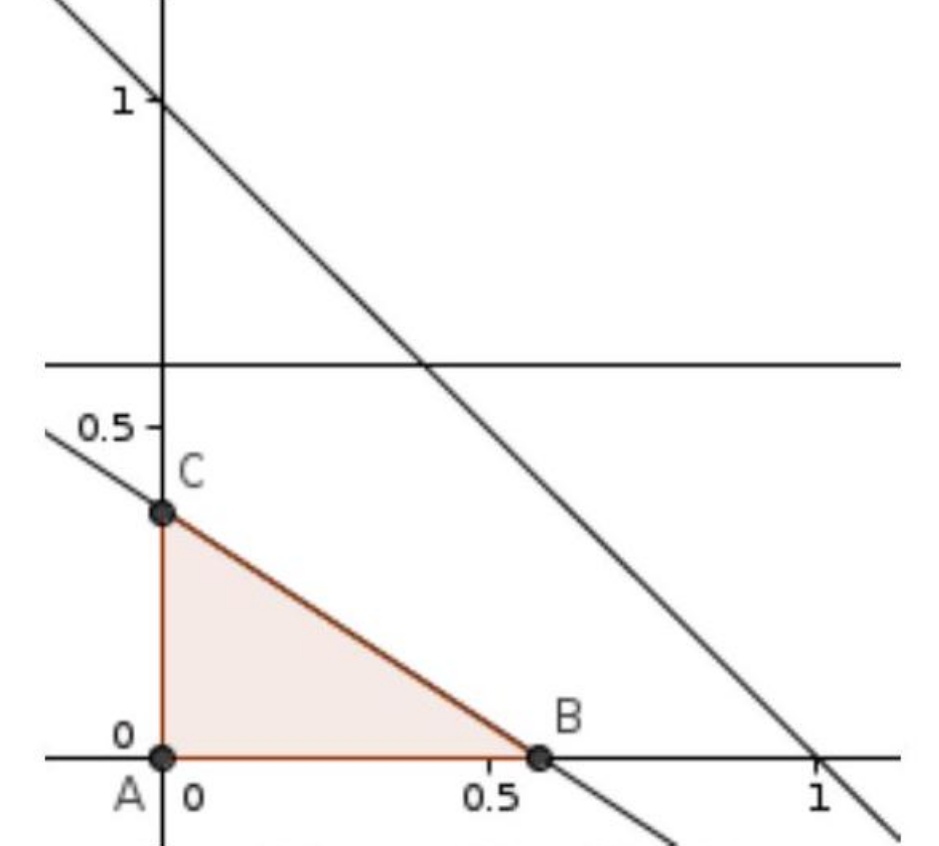
Пусть . Тогда, с учётом допустимых значений
, неравенство равносильно системе
Решения этой системы - точки на полуокружности , лежащие ниже графика функции
.
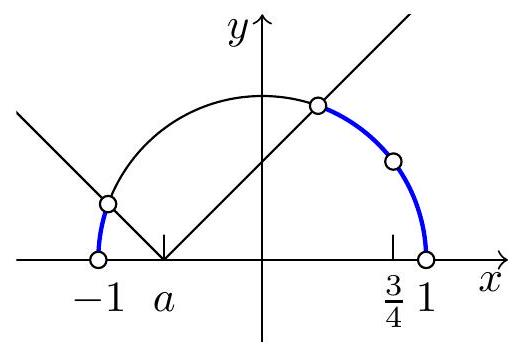
При изменении параметра график функции
перемещается вдоль оси
. При значениях
, близких к
в
качестве множества решений имеем
непересекающихся интервала. При значениях
, близких к
получается
интервала.
Крайнее положение графика, при котором получается два интервала, изображено на рисунке:
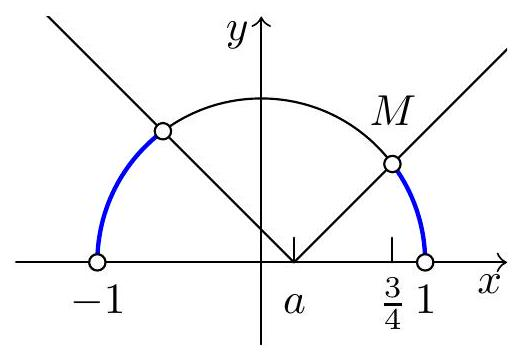
Координаты точки пересечения окружности и прямой
равны
Так как , то
.
Таким образом, ответом является множество
Ошибка.
Попробуйте повторить позже
Решите систему уравнений
Источники:
Подсказка 1
Сразу понимаем, что, скорее всего, эта система "нормально" не решается. У нас два уравнения с кучей неизвестных. Но одно из решений мы сразу угадываем — это один из x равен 3, а остальные 0. Давайте поделим обе части первого уравнения на 3¹⁰. Как тогда можно оценить каждое из слагаемых?
Подсказка 2
Ага, тогда понятно, что каждое из слагаемых не превосходит единицы, так как степень у них чётная. Значит, для любого 1≤k≤92 получаем, что |x_k/3|≤1. Не забываем про модуль, так как извлекаем корень из чётной степени. Но раз у нас число меньше 1 то, что можно сказать о нём при возведении в степень?
Подсказка 3
Верно, тогда это число в 33 степени меньше, чем в 10. Теперь, учитывая это, попробуйте записать неравенство для второго и первого уравнения, используя неравенство с модулем. Выходит, что возможен только случай равенства |x_k/3|³³ = |x_k/3|¹⁰ для данных k.
Заметим, что
Тогда для каждого имеем
откуда
Окончательно получим
Значит, для каждого выполнено
откуда
Отсюда несложно получаем, что тогда один из равен
а все остальные равны
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и боковыми сторонами
. Точка
на прямой
такова, что
периметр треугольника
наименьший из возможных. Найдите этот периметр.
Источники:
Подсказка 1
Заметим, что основание у нашего треугольника зафиксировано. То есть на самом деле нам нужно найти минимальную сумму расстояний до точки P от A и B. Давайте попробуем понять, почему расстояние будет минимальным, когда лучи PA и PB будут падать под одним углом на BC. Обычно когда речь идёт о минимуме или максимуме, то нужно неравенство, а в геометрии чаще всего — это неравенство треугольника. Как можно попробовать сделать из отрезков PA и PB треугольник, в котором мы явно будем видеть их сумму?
Подсказка 2
Верно, хоть до этого и не просто догадаться, давайте попробуем отразить точку D симметрично относительно BC. Что тогда у нас получается? Пусть симметричная точка X. Получается треугольник APX, где сумма наших расстояний это AP+PX. Но тогда записав неравенство треугольника, когда достигается минимум?
Подсказка 3
Да, получается, чтобы сумма расстояний выстроилась в одну прямую, а это и будет минимум по неравенству треугольника, нужно как раз равенство углов. Победа! Теперь осталась только техническая часть поиска двух сторон равнобедренного треугольника APD. Это можно сделать, например, через теорему Пифагора для половины основания, высоты и стороны треугольника. Нужно только найти высоту трапеции, что при наличии стольких данных несложно.
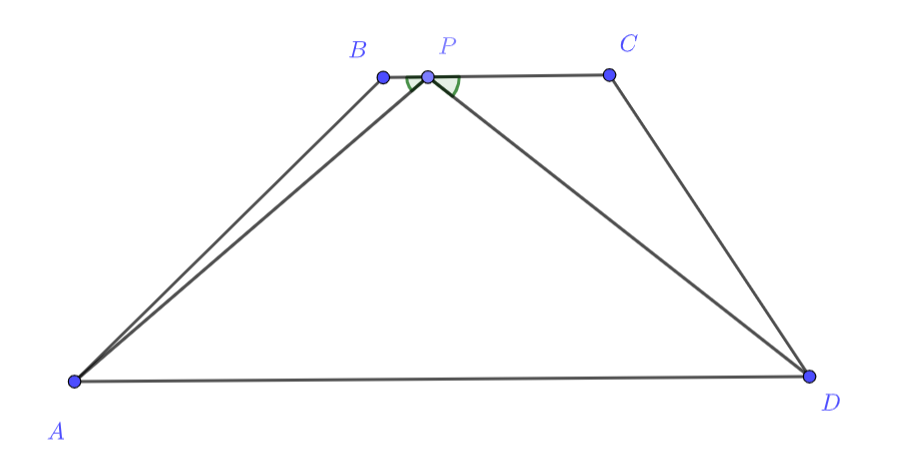
Первое решение.
Воспользуемся следующим утверждением, которое наиболее известно как «принцип наименьшего времени Ферма» в физике:
Для данных точек и данной прямой
из всех точек
сумма
будет минимальной, когда углы между прямыми
и
и
и
будут равны.
Тогда для искомой точки на прямой
должно выполняться равенство
(точки
и
- где-то «далеко» на
прямой
. Поскольку
, то
т.е. треугольник - равнобедренный. Значит, нам достаточно найти периметр равнобедренного треугольника
, где
- точка
на прямой
.
По теореме Пифагора этот периметр равен
где - расстояние между прямыми
и
, т.е. высота трапеции.
Найти высоту трапеции можно разными способами. Например, проведём через точку , прямую, параллельную
, до пересечения с
основанием
в точке
. Тогда искомая высота - это высота из вершины
в треугольнике
. Поскольку
параллелограмм, то
,
.
Итого, нам достаточно найти длину высоты на сторону длины 7 в треугольнике со сторонами 5 , . По формуле площади и
формуле Герона имеем
откуда
и окончательный ответ .
Второе решение.
Также, как и в первом решении, найдём высоту трапеции. Покажем здесь, как можно это было сделать по-другому. Опустим высоты
и
трапеции. Обозначим их длины через
, длину отрезка
обозначим через
. Поскольку
, для
получим
. Из прямоугольных треугольников
и
по теореме Пифагора получим
и
Подставив в эти равенства известные длины, получим систему уравнений
Вычитая из первого равенства второе, получим , откуда
. Тогда
.
Рассмотрим треугольник . Обозначим
, тогда
(здесь и далее все расстояния со знаком, т.е. могут быть
отрицательные). Опустим высоту
. Тогда треугольник
прямоугольный и по теореме Пифагора
Аналогично, из прямоугольного треугольника
Тогда периметр треугольника равен
Найдём производную этой функции:
Из уравнения получаем
откуда . Несложно видеть, что
именно точка минимума, откуда минимальный периметр равен
.
Ошибка.
Попробуйте повторить позже
На заводе имеются в достаточном количестве три сплава титана, алюминия и молибдена. Все сплавы с примесями. Процентное содержание компонентов в этих сплавах приведено в таблице.
| 1 | 2 | 3 | |
| Молибден | | | |
| Титан | | | |
| Алюминий | | | |
Из этих сплавов необходимо приготовить новый сплав, в котором алюминия должно быть не больше , а молибдена - не меньше
.
Какое наибольшее и какое наименьшее содержание титана (в процентах) может быть в этом сплаве?
Источники:
Подсказка 1
Давайте сначала просто посчитаем. Пусть мы взяли x,y и 1-x-y первого, второго и третьего сплавов соответственно. Тогда как выглядят наши условия на нужный сплав и что мы хотим максимизировать/минимизировать?
Подсказка 2
Вы получили условия в виде неравенства для x и y, и выражение, которое надо максимизировать/минимизировать. Может быть, на плоскости эти неравенства будут нагляднее?)
Подсказка 3
Нам по факту надо найти макс/мин выражения 6+30x+15y. Понятно, что минимум будет в точке (0, 0). А чтобы найти максимум, можно заметить, что коэф при x больше, чем коэф при y....)
Первое решение.
Заметим, что как бы ни изготавливали новый сплав, содержание титана в нём будет не меньше минимального из содержаний
титана в имеющихся сплавах. Поэтому содержание титана в любом изготовленном сплаве будет не менее . С другой
стороны, сплав 3 подходит под условия на содержание алюминия и молибдена. Значит, наименьшее содержание титана
.
Теперь найдём наибольшее содержание титана в таком сплаве. Заметим, что если при изготовлении нового сплава мы использовали сплав 2, то можно его заменить на сплав 1: от этого содержание алюминия уменьшится, а молибдена и титана - увеличится. Поэтому в сплаве с наибольшим содержанием титана не участвует сплав 2.
Сразу отметим, что тогда в таком сплаве будет молибдена, т.е. он подходит под условие на молибден. В сплаве 1 титана больше, чем
в сплаве 3 , но сплав 1 не подходит под условие на алюминий. Понятно, что чем меньше мы возьмём сплава 3, тем больше будет титана в
изготовленном сплаве. Возьмём ровно столько, чтобы выполнилось условие на алюминий:
и
масса сплава 1 и 3
соответственно), откуда
, т.е. можно взять 23 части сплава 1 и 17 частей сплава 3. Тогда содержание титана в процентах
будет
Второе решение.
Пусть взято и
первого, второго и третьего сплава соответственно, причём
. Тогда условия
задачи можно записать так:
Изобразим на координатной плоскости область (см. рисунок), удовлетворяющую системе неравенств
Процентное содержание титана . Легко видеть, что минимум этого числа достигается в точке
и равен 6 . Чтобы найти максимум, заметим, что абсцисса точки
равна
, а ордината точки
. При этом
коэффициент при
в
больше. Значит, значение в точке
точно больше (мы большее число умножаем на большее число), и равно
наименьшее
наибольшее
Ошибка.
Попробуйте повторить позже
При каком наименьшем можно покрасить каждое натуральное число в один из
цветов так, чтобы любые два числа, отличающиеся на
5 , на 8 , на 10 , на 13 и на 18, были покрашены в разные цвета?
Источники:
Подсказка 1
Давайте попробуем как-то снизу оценить кол-во цветов. Вот что можно заметить в этих разностях: 18-13 = 5, 18-10 = 8, 13-5 = 8, 13-5 = 8....может быть можно найти какую-то группу чисел, в которой все числа должны быть разного цвета?
Подсказка 2
Например, подойдет четверка чисел вида n, n+5, n+10, n+18! А еще подойдет четверка n, n+5, n+13, n+18...теперь проверьте, может ли быть ровно 4 цвета?
Подсказка 3
Для четырех не вышло, давайте попробуем для 5! Может попробовать разбить все числа на какие-то группы, что внутри одной группы разность между числами либо очень маленькая, либо очень большая...тогда, скорее всего, условие выполнится)
Докажем для начала, что четырьмя и меньше цветами обойтись не удастся. Посмотрим на числа . Разности между
ними равны
т.е. любые два из этих чисел покрашены в различные цвета. Значит, цветов хотя бы четыре. Предположим, что цветов ровно четыре.
Тогда числа покрашены во все возможные цвета. Аналогично можно получить, что во все возможные цвета
покрашены числа
,
. Значит, для каждого натурального
числа
и
должны быть покрашены в один
и тот же цвет.
Применим полученное утверждение для . Тогда числа
покрашены в один и тот же цвет. Противоречие,
ведь
и числа 11 и 29 должны быть покрашены в разные цвета.
Докажем теперь, что пять цветов достаточно. Для этого разобьём все натуральные числа на группы по 5 подряд идущих чисел, а группы
покрасим так: первую - в первый, вторую - во второй, ..., пятую - в пятый, шестую - в первый, седьмую - во второй, .... При такой раскраске
числа одного цвета будут или отличаться не более чем на 4, если лежат в одной пятёрке, или хотя бы на 21 - если в разных. Значит, числа,
отличающиеся на и 18, будут покрашены в разные цвета.
Ошибка.
Попробуйте повторить позже
Точка — середина отрезка
; точка
— середина отрезка
; для каждого
точка
— середина отрезка
.
Пусть
— предельное положение точки
при
. Найдите длину отрезка
, если длина отрезка
равна
Источники:
Подсказка 1
Порисуйте эти точки на отрезке. В каком порядке они будут располагаться?
Подсказка 2
Они будут идти как-то так: S, R_2, R_4..., R,...R_3, R_1, T. Еще осталось понять, чему равна длина отрезка вида R_{n+2}R_n и дело в шляпе!
Обозначим , тогда
- середина отрезка
для каждого
. Легко видеть, что на отрезке точки будут
расположены в следующем порядке:
Поэтому
Далее, длина отрезка в два раза меньше длины отрезка
, откуда длина отрезка
в четыре раза меньше
длины отрезка
. Значит,



