Алгебра. Исследование замены —Каталог задач по ЕГЭ - Математика

Тема 18. Задачи с параметром

18.08 Алгебра. Исследование замены

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#20551

При каких значениях $a$ уравнение

a2 3 x2 − |x| + 1= 0

имеет как минимум два решения?

Показать ответ и решение

Сделаем замену $-1= y, |x|$ $y > 0.$ Тогда $a2= a2y2 x2$ и исходное уравнение эквивалентно следующей системе:

{ a2y2− 3y+ 1= 0 y > 0

При этом зная, что решение системы $y0 > 0,$ можно найти корни исходного уравнения, сделав обратную замену:

-1 = y0 ⇔ |x|= -1 ⇔ x = ±-1 |x| y0 y0

(1)

Такие корни будут различными, а значит исходное уравнение будет иметь как минимум два различных корня.

Найдем значения $a,$ при которых уравнение $2 2 a y − 3y+ 1= 0$ имеет хотя бы один положительный корень.

При $a= 0$ уравнение примет вид

$pict$

Тогда исходное уравнение будет иметь корни $± 3$ по формуле (1), то есть корней как минимум два, что нам подходит.

При $a⁄= 0$ уравнение будет квадратным.

$pict$

Квадратное уравнение имеет два (не обязательно различных) корня при $D ≥ 0.$ Обозначим их за $y1$ и $y2$ . По теореме Виета произведение корней равно $y1⋅y2 = 1a2-> 0,$ то есть оба корня одного знака. При этом также по теореме Виета сумма корней равна $3a2-> 0,$ откуда следует, что оба корня положительны.

Таким образом, уравнение имеет хотя бы один положительный корень при любых $a,$ для которых $D ≥ 0.$ Найдем значения $a,$ при которых верно данное неравенство:

$pict$

Получили, что исходное уравнение имеет хотя бы два корня при одном из следующих условий:

$pict$

Таким образом, $[ ] a ∈ − 3; 3 . 2 2$

Ответ:

$[ ] − 3; 3 2 2$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Не рассмотрен случай $a =0$	3

Верно наложены все условия при $D ≥0,$ но в ходе решения допущена ошибка	2

Сделана замена, верно введены ограничения на замену, рассмотрен случай $a =0$	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#18382

При каких значениях параметра $a$ уравнение

2 2a(x +1) − |x + 1|+ 1= 0

имеет четыре различных корня?

Показать ответ и решение

Сделав замену $|x +1|= t,$ получим уравнение, почти всегда квадратное, кроме случая $a= 0,$ при котором оно вырождается в линейное:

2at2− t+ 1= 0 (∗)

Исследуем замену, то есть для каждого фиксированного $t$ определим, какое количество решений относительно переменной $x$ мы получим, делая обратную замену:

при $t> 0$ имеем два корня $x;$
при $t= 0$ имеем один корень $x;$
при $t< 0$ не имеем корней $x.$

Так как уравнение $(∗)$ может иметь максимум два корня $t,$ то наибольшее количество корней исходного уравнения — четыре, что и требуется.

Следовательно, единственный подходящий вариант: уравнение $(∗)$ является квадратным и имеет два корня, причем положительных.

Это обеспечивается следующими условиями, которые нужно записать в системе:

$a⁄= 0,$ так как уравнение $(∗)$ — квадратное;
$D = 1− 8a > 0,$ так как уравнение имеет два корня $t;$
$1-> 0, 2a$ так как для двух положительных корней произведение положительно;
$12a > 0,$ так как для двух положительных корней сумма положительна.

Решая эти неравенства и пересекая их решения, получаем

( 1 ) a ∈ 0;8

Ответ:

$( 1) a ∈ 0;8$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Не рассмотрен случай $a= 0$ (нет пояснения, что уравнение квадратное при $a ⁄=0$ )	3

Верно наложены все условия для существования двух положительных значений $t,$ но либо полученная система не решена, либо решена с ошибкой и найдены неверные значения $a$	2

Верно рассмотрен случай $a =0$ и при $a ⁄=0$ уравнение сведено к квадратному относительно новой переменной, например, $t$ и указаны её допустимые значения	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 3#2565

Найдите все значения параметра $a,$ при каждом из которых уравнение

( sinx ) 2 ( sinx ) sinx+1 2 − 1 a − 3⋅2 − 1 a+ 2 = 0

имеет хотя бы один корень.

Показать ответ и решение

Сделаем замену $sinx t= 2 .$ Так как $sin x∈ [− 1;1],$ то $[1 ] t∈ 2;2 .$ Следовательно, нужно найти те $a,$ при которых уравнение будет иметь хотя бы одно решение $t$ из отрезка $[ ] 1 2;2 .$ Приведя подобные слагаемые, можем переписать уравнение в виде

(a− 1)(a− 2)t= a(a − 1)

Рассмотрим несколько случаев в зависимости от значений параметра $a.$

1) $a= 1.$ Тогда уравнение примет вид $0 = 0.$ Решением данного уравнения являются все $t.$ Следовательно, этот случай нам подходит.

2) $a= 2.$ Тогда уравнение примет вид $0 = 2.$ Такое уравнение не имеет решений. Следовательно, этот случай нам не подходит.

3) $a⁄= 1;2.$ Тогда имеем:

a t= a-− 2

Нам нужно, чтобы $[ ] t∈ 1;2 . 2$ Следовательно,

1 -a-- 2 ≤ a− 2 ≤ 2 ⇔ a ∈ (− ∞;− 2]∪ [4;+∞ )

В данном множестве не содержатся точки $a= 1;2.$

Объединяя случаи, получаем окончательно

a ∈(− ∞;−2]∪ {1}∪[4;+∞ )

Ответ:

$(−∞; −2]∪ {1} ∪[4;+ ∞)$

Ошибка.
Попробуйте повторить позже

Задача 4#571

Найдите все значения параметра $a,$ при каждом из которых уравнение

x x 16 +(a− 4)⋅4 + 3(1 − a) =0

имеет решение.

Показать ответ и решение

Данное уравнение с помощью замены $4x = t$ сводится к квадратному:

2 t + (a− 4)t+ 3(1− a)= 0 (∗)

Заметим, что так как $4x > 0,$ то $t> 0.$ Найдем значения $a,$ при которых уравнение $(∗)$ не имеет решений либо имеет решения, но все они $≤0.$ Тогда все остальные значения $a$ пойдут в ответ.

Для этого нужно, чтобы парабола $y =t2+ (a− 4)t+ 3(1− a),$ ветви которой при любом $a$ направлены вверх, имела один из следующих видов:

$PIC$

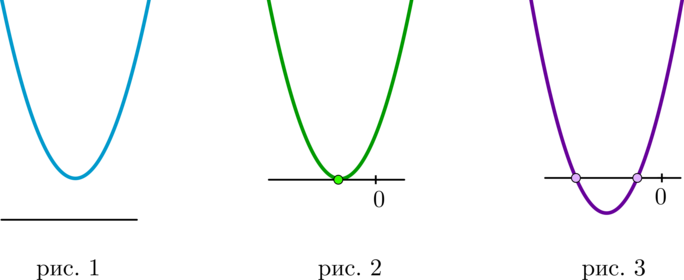
Рис. 1: $D < 0,$ уравнение не имеет корней;

Рис. 2: $D = 0,$ уравнение имеет один корень $4−a t= 2-,$ который находится не правее 0;

Рис. 3: $D > 0,$ уравнение имеет два корня, причем оба корня находятся не правее 0.

Все эти случаи записываются следующим образом:

⌊ D( < 0 ||{ D =0 ||( 4−-a ||| tв = 2 ≤ 0 ||(|| D >0 ||{ 4−-a ⌈||( tв = 2 < 0 y(0)≥ 0

Здесь $tв$ — абсцисса вершины параболы.

Решив данную совокупность, получим

a∈ ∅

Следовательно, исходное уравнение имеет решение при

a ∈(−∞; +∞ )

Ответ:

$a ∈(−∞; +∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Необоснованные переходы по ходу исследования	3

Верно наложены все условия, но либо полученные системы не решены, либо решены с ошибкой и найдены неверные значения $a$	2

Уравнение сведено к квадратному относительно новой переменной, например, $t$ и указаны её допустимые значения	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 5#46569

Найдите все положительные значения параметра $a,$ при каждом из которых уравнение

x √ -x---- 2 − a= 4 − 3a

имеет единственный корень.

Показать ответ и решение

Сделаем замену $2x = t,$ $t> 0.$ Тогда уравнение примет вид

∘-2---- t− a = t − 3a

Это уравнение равносильно системе

{ 2 2 ({ a +3 (t− a) = t − 3a ⇒ t= --2-, если a⁄= 0 t− a ≥ 0 (t≥ a

Для того, чтобы уравнение имело 1 решение, необходимо, чтобы

a+-3 ≥a и a+-3 > 0 ⇔ −3 <a ≤ 3 2 2

Учитывая то, что $a> 0$ по условию, получаем

a∈ (0;3]

Ответ:

$a ∈(0;3]$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточно обоснованные переходы	3

Все неравенства для выполнения условия задания составлены верно, но в решении есть ошибка	2
ИЛИ
неравенства решены верно, но не учтено, что по условию $a >0$

Верно сведено к линейному уравнению относительно новой переменной с учетом ограничений	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 6#38365

Найдите все значения параметра $a,$ при каждом из которых уравнение

( -x2--)2 -3ax2 (a +1) x2+ 1 − x2 +1 + 4a = 0

имеет хотя бы одно решение.

Показать ответ и решение

Сделаем замену $t= -x22- x +1$ и исследуем ее. Если взять за $p= x2,$ то $p≥ 0$ и

-p-- -1-- t= p+ 1 = 1 − p+ 1

Графиком функции $y = t(p)$ является часть гиперболы при $p≥ 0$ . Чтобы построить эту гиперболу, нужно гиперболу $y = − 1p$ сдвинуть на 1 влево и на 1 вверх. Тогда при $p≥ 0$ получим часть ветви:

$PIC$

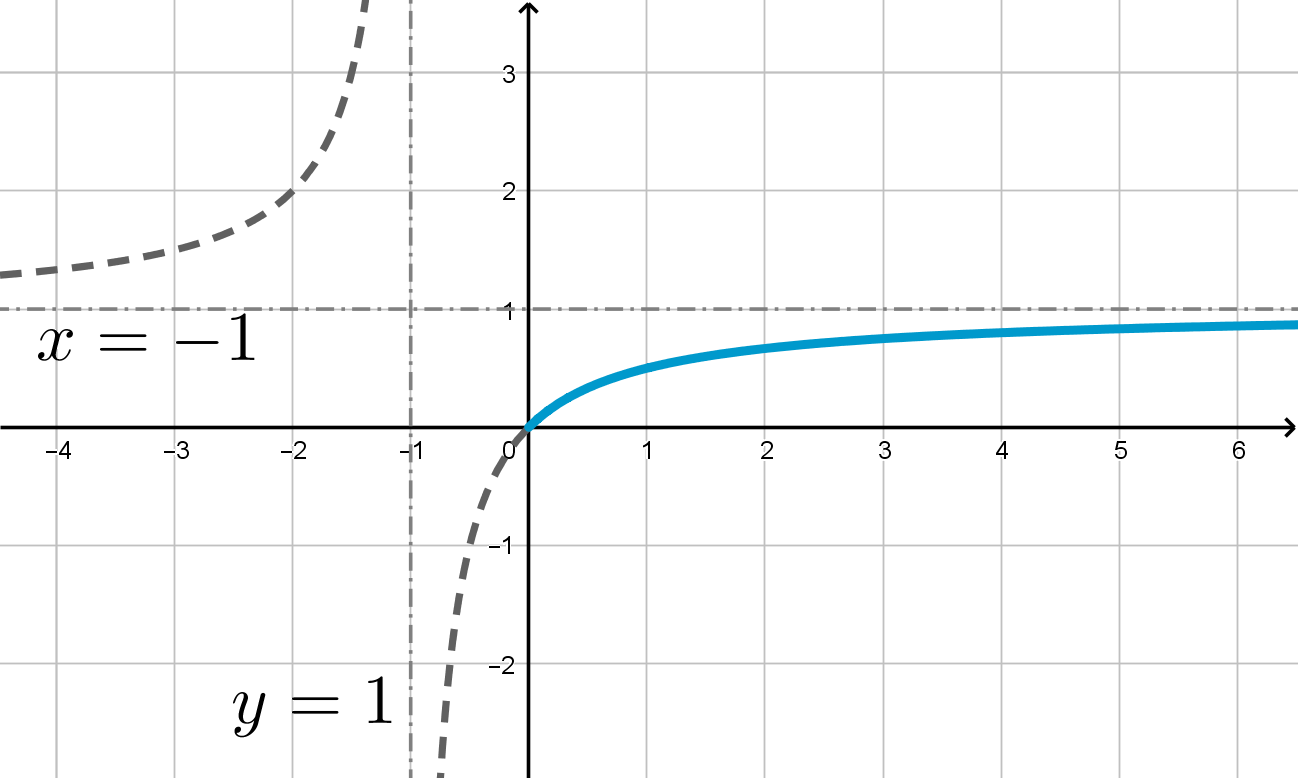
То есть $t(p)∈ [0;1).$ Следовательно, исходное уравнение будет иметь хотя бы одно решение, если уравнение

(a+ 1)t2− 3at+4a = 0

имеет хотя бы один корень из промежутка $[0;1).$

Заметим, что это уравнение может вырождаться в линейное. Поэтому рассмотрим следующие случаи:

1)

$a= −1.$ Тогда уравнение примет вид

4 t= 3 ∕∈ [0;1)

Следовательно, этот случай нам не подходит.

2)

$a⁄= −1.$ Тогда уравнение квадратное и имеет решения, если его дискриминант неотрицателен:

2 D = −7a − 16a≥ 0

2.1)

$D =0,$ откуда $16 a = − 7 ;0.$ Тогда единственным корнем уравнения является абсцисса $tверш$ вершины параболы, следовательно,

3a tверш = 2(a+-1) ∈ [0;1) ⇔ 0≤ a < 2

Из чисел $a =− 16;0 7$ в этом промежутке лежит лишь число $a = 0.$ То есть это значение параметра пойдет в ответ.

2.2)

$D >0,$ откуда $− 16< a< 0. 7$ Тогда, учитывая, что ветви параболы не зафиксированы и случай $y(1)= 0$ мы рассмотрим отдельно, а также то, что при этих значениях параметра $tверш ∕∈ (0;1)$ (то есть оба корня не могут лежать в промежутке $[0;1)$ ), нам подходят следующие 4 случая:

$PIC$

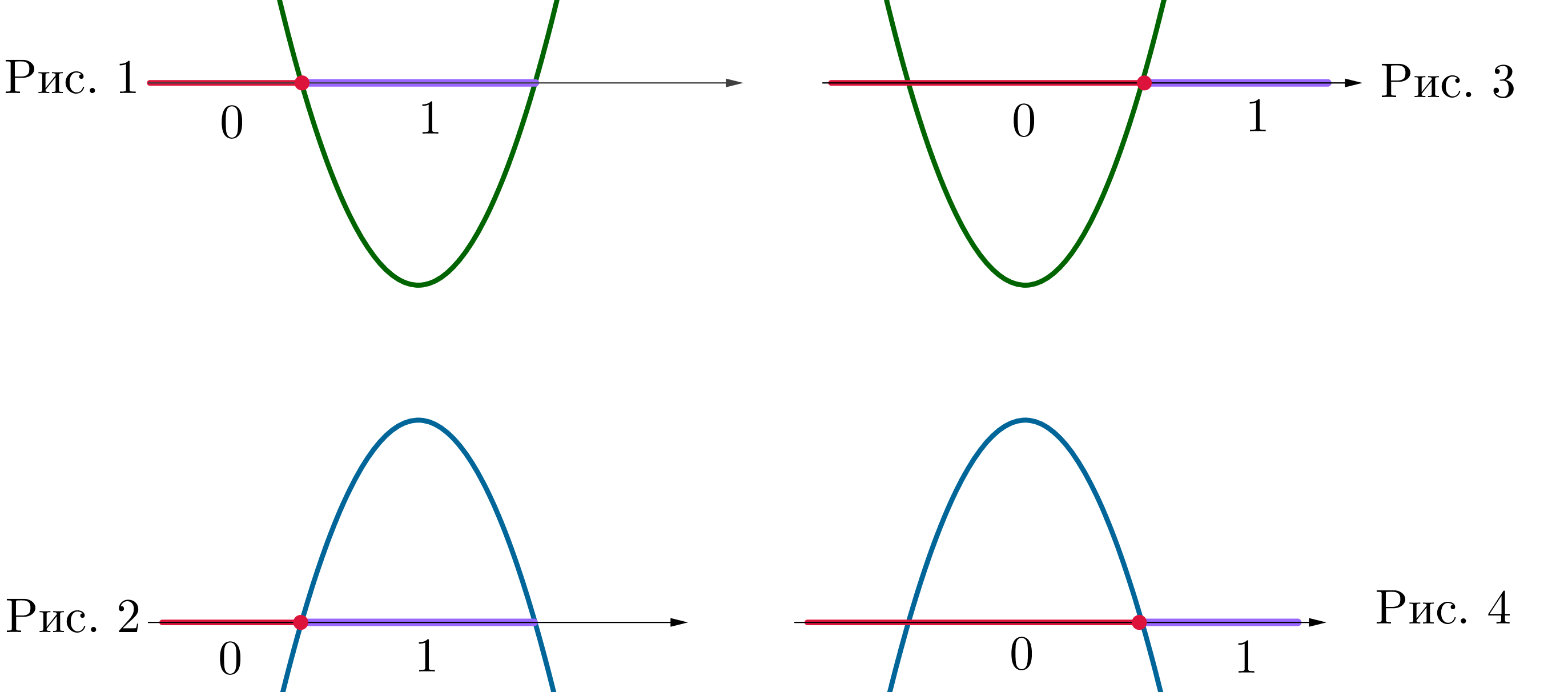
$y(1)= 0,$ то есть

1 a + 1− 3a + 4a = 0 ⇔ a= − 2

Отсюда, так как произведение корней равно $4a,$ получаем, что второй корень равен $4a:1= − 2.$ Таким образом, этот случай нам не подходит, так как нет ни одного корня из промежутка $[0;1).$

Пусть $y(1) ⁄=0.$ Рассмотрим каждый рисунок в отдельности:

1:: Ветви параболы направлены вверх, число 1 находится между корнями, число 0 находится левее меньшего корня либо совпадает с ним.
Эта ситуация задается следующей системой:
$({ y(1)< 0 ( y(0)≥ 0$
2:: Ветви параболы направлены вниз, число 1 находится между корнями, число 0 находится левее меньшего корня либо совпадает с ним. $({ y(1)> 0 ( y(0)≤ 0$

Эти две системы можно объединить в следующую:

( ( ||{y(0)≤ 0 ||{--4a- ≤ 0 y(1) ⇒ 2a +1 ⇔ a ∈∅ ||(tверш >0 ||(---3a---> 0 2(a+ 1)

3:

Ветви параболы направлены вверх, число 1 находится правее большего корня, число 0 находится левее большего корня либо совпадает с ним.

Если найти множество $A1$ значений параметра, при которых число 0 находится правее большего корня при условии, что ветви направлены вверх, то при всех $ℝ ∖A1$ число 0 находится левее большего корня или совпадает с ним (при выполнении всех условий тех случаев, в которых мы находимся, то есть при $D > 0$ И $y(1)⁄= 0$ ). Тогда условие нашей картинки будет выглядеть следующим образом:

$(| ||{ a∈ ℝ∖A1 | y(1)> 0 ||( tверш < 1$ (cases 1)

Найдем $A1 :$

( (| a+ 1> 0 || a> − 1 ||{ ||{ | y(0) > 0 ⇔ | 4a> 0 ⇔ a∈ ∅ ||( tверш < 0 |||( 3 ⋅-a-- <0 2 a+ 1

Тогда система cases 1 равносильна:

(| |||{a ∈ℝ 2a+ 1 >0 ⇔ − 1 < a< 2 ||||a − 2 2 (a-+1 < 0

Пересекая с $D > 0$ и $y(1)⁄= 0,$ получаем значения параметра, идущие в ответ:

− 1 < a< 0 2

4:

Ветви параболы направлены вниз, число 1 находится правее большего корня, число 0 находится левее большего корня либо совпадает с ним.

Аналогично предыдущему случаю (но ветви направлены вниз):

$( |||{ a∈ ℝ∖A2 y(1)< 0 |||( tверш < 1$ (cases 2)

Найдем $A2 :$

( (| |||{ a+ 1< 0 |||{ a< − 1 y(0) < 0 ⇔ 4a< 0 ⇔ a∈ ∅ |||( |||| 3 a tверш < 0 ( 2 ⋅a+-1 <0

Тогда система cases 2 равносильна:

( || a∈ ℝ |||| { a< − 1 ⇔ a∈ ∅ ||| 2 |||( a−-2 < 0 a+ 1

Объединяя $a= 0$ с $− 12 < a <0,$ получаем итоговый ответ

( ] a ∈ − 1;0 2

Ответ:

$a ∈(−0,5;0]$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Не рассмотрен случай линейного уравнения или случай $D = 0$	3

Верно рассмотрен случай линейного уравнения и $D = 0,$ но в случае при $D >0$ либо не все случаи учтены, либо в ходе решения допущена ошибка	2

Введена и исследована замена, при этом может быть рассмотрен случай линейного уравнения	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#38363

Найдите $a$ , при которых неравенство

x2+ 4x+ 6a|x+ 2|+ 9a2 ≤ 0

имеет более одного решения.

Показать ответ и решение

Выделим полный квадрат:

(x+ 2)2 +6a|x+ 2|+9a2− 4 ≤0

Так как $k2 = |k|2$ , то неравенство при $t= |x+ 2|$ равносильно

t2+ 6at+9a2− 4≤ 0 ⇔ (t+ 3a)2 − 4 ≤ 0 (⋆)

Рассмотрим функцию $y = (t+ 3a)2− 4$ . Графиком является парабола, сдвинутая на $4$ единицы вниз и на $3a$ единиц по горизонтали. Так как $t= |x+ 2|$ , то исходное неравенство будет иметь решения тогда и только тогда, когда у неравенства $(⋆)$ есть хотя бы два решения $t≥ 0$ . Следовательно, график должен выглядеть следующим образом:

$PIC$

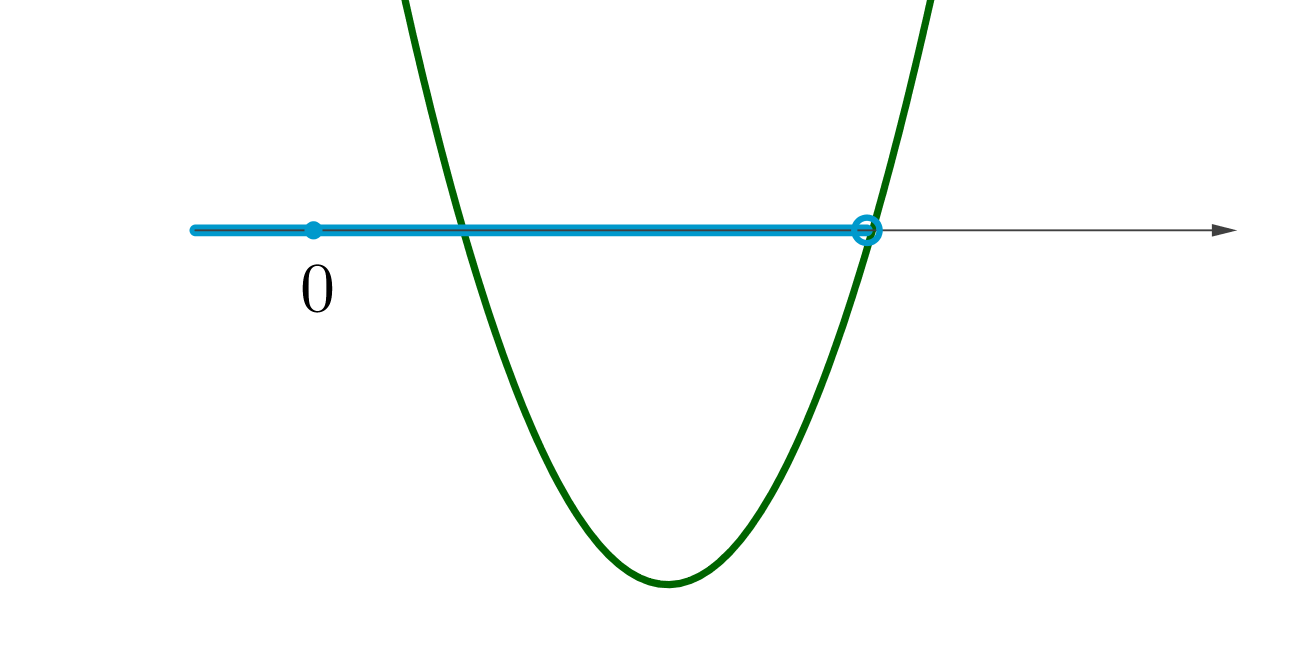
То есть точка $t= 0$ должна находиться левее большего корня.

⌊y(0)< 0 |( ||{ y(0) ≥0 ⌈( tверш > 0

Первое неравенство совокупности задает положение точки $t= 0$ между корнями. Система задает положение этой точки левее меньшего корня либо совпадение с ним. Дорешаем совокупность:

⌊ ⌊ 2 ⌊ 9a2 − 4 < 0 ||a|< 3 |a|< 2 ||| ({ 2 ⇔ |||( ⇔ || 3 ⇔ a < 2 ⌈ 9a − 4 ≥0 |⌈{ |a|≥ 23 ⌈ 2 3 (− 3a> 0 ( a< 0 a≤ − 3

Ответ:

$a ∈(− ∞; 2) 3$

Ошибка.
Попробуйте повторить позже

Задача 8#38362

Найдите все $a$ , при которых уравнения

(x2− 6|x|+ a)2+ 10(x2− 6|x|+ a)+ 26= cos 16π a

имеет ровно два различных корня.

Показать ответ и решение

Сделаем замену $t= x2− 6|x|+ a= (|x|− 3)2 +a − 9$ . Тогда уравнение примет вид

2 16π 2 16π t + 10t+26 = cos a ⇔ (t +5) = cos a − 1

Так как $cosα ∈[−1;1]$ , то $cosα− 1∈ [− 2;0]$ . Следовательно, правая часть равенства $≤ 0$ . Левая же часть равенства как полный квадрат $≥ 0$ . Следовательно, равенство возможно только в том случае, когда обе части равенства равны $0$ :

(|{ cos 16π-= 1 (|{ 16π =2πn,n ∈ℤ a ⇒ a |( t= −5 |( (|x|− 3)2 = 4 − a (⋆)

Уравнение $2 A =B$ имеет 0, 1 или 2 решения. Уравнение $|C|= D$ также имеет 0, 1 или 2 решения. Следовательно, уравнение $(⋆)$ может иметь от 0 до 4 решений.

2 решения оно имеет, если

квадратное уравнение имеет два решения, а из получаемых двух модульных уравнений одно имеет два решения, а другое – не имеет решений.
Это выполняется, если $4− a> 0$ , откуда $|x|= 3± √4−-a$ и $3+ √4−-a >0$ , $3− √4−-a <0$ . Получаем $a <− 5$ .
квадратное уравнение имеет одно решение, а получаемое модульное уравнение имеет два решения.
Это выполняется, если $4− a= 0$ , откуда $|x|= 3$ , откуда $x= ±3$ . Следовательно, $a= 4$ .

Ответ:

$a ∈{− 8;4}$

Ошибка.
Попробуйте повторить позже

Задача 9#38361

Найдите $a$ , при которых уравнение

a⋅41x−1+ (a− 1)⋅2 1x − a3+ 3a− 2= 0

не имеет корней.

Показать ответ и решение

Выражение $y = 1− 1 x$ определено при всех $x⁄= 0$ и принимает все значения, кроме $− 1$ . Если сделать замену $1x−1 2 = t$ , то имеем $t∈ (0;0,5)∪ (0,5;+∞ )$ , причем каждое такое значение $t$ дает ровно одно значение для $x$ . Получим следующее уравнение:

at2+ 2(a− 1)t − (a3− 3a+ 2)= 0

Оно линейное при $a =0$ и квадратное при $a⁄= 0$ . Чтобы исходное уравнение не имело решений, нужно, чтобы новое уравнение: 1) не имело решений; 2) имело решения и все они были из промежутка $(−∞; 0]∪{0,5}$ .

Если $a = 0$ , получим: $t= −1$ . Подходит.

Если $a ⁄= 0$ . Найдем, при каких $a$ у уравнения есть корень $t= 0,5$ :

a + a− 1− (a3− 3a +2)= 0 ⇔ 4a3− 17a+ 12= 0 4

Найдем, при каких $a$ у уравнения есть корень $0$ :

3 2 a − 3a+ 2= 0 ⇔ (a− 1)(a+ 2)= 0 ⇔ a =− 2;1

Подбором находим рациональный корень $3 a = 2$ . С помощью деления в столбик левой части на $2a− 3$ находим разложение:

3 3± √41 (2a− 3)(2a2+ 3a− 4)= 0 ⇔ a= 2;− --4----

Выпишем дискриминант:

D = 4(a − 1)2(a+ 1)2 ≥0

При $a= ±1$ дискриминант $D = 0$ , следовательно, имеется один корень $t0 = 1−a a$ , который не равен $0,5$ . Следовательно, он должен быть $≤ 0$ . При $a = 1$ он равен нулю, а при $a= − 1$ равен $− 2$ . Подходит $a =±1$ .

При $a⁄= ±1$ дискриминант положительный. Будем рассматривать уравнение в виде

2 2(1− a)t a3− 3a + 2 t − ---a--- − ----a----= 0

При $a= −2$ один корень $t1 =0$ , а другой $t2 = −3$ . Все хорошо.

При $a⁄= −2;±1$ у уравнения два корня, не равные нулю. Если один из них $t1 = 0,5$ , то другой должен быть отрицательный, значит, и произведение отрицательное:

a3-− 3a-+2 − a < 0 ⇔ a∈ (−∞; −2)∪(0;1)∪(1;+∞ )

Все $3 3 ±√41- a = 2;−---4---$ этому удовлетворяют.

При всех оставшихся $a$ у уравнения два корня, не равные ни $0,5$ , ни $0$ . Значит, оба должны быть отрицательными, то есть их произведение должно быть положительным, а сумма – отрицательной:

( ||{ 2(1-− a)-< 0 ({ a ⇔ a∈ (−∞;0)∪ (1;+ ∞) ⇔ a∈ (−2;0) ||(− a3−-3a+-2 >0 ( a∈ (−2;0) a

Ответ:

$− 2 ≤ a≤ 0;a= 1; 3; −3±-√41 2 4$

Ошибка.
Попробуйте повторить позже

Задача 10#37055

Найдите $a,$ при которых уравнение

2 2 2 (a + 8a+ 16)(2− 2cosx− sin x)+ (32+ 2a +16a)(cosx− 1)+ 3a+ 10= 0

не имеет корней.

Показать ответ и решение

Выражение

2 2 2 2 − 2 cosx − sin x= cosx − 2cosx + 1= (cosx − 1)

Сделаем замену $t =cosx − 1$ , тогда уравнение примет вид (и сразу введем функцию)

2 2 2 y = (a+ 4)t + 2(a +4) t+3a +10 = 0

Заметим, что $t∈ [−2;0]$ , следовательно, исходное уравнение не будет иметь решений, если новое уравнение не будет иметь решений либо будет иметь решения, но не из этого отрезка.

1) $a= − 4$ , тогда уравнение линейное и приобретает вид $− 2= 0$ . Такое уравнение не имеет решений, следовательно, данное $a$ нам подходит.

2) Пусть $a⁄= −4$ . Тогда
$D = 4(a+ 4)4 − 4(3a+ 10)(a+ 4)2 = 4(a +4)2(a2 +5a +6)= 4(a+ 4)2(a+ 2)(a +3)$ . Рассмотрим случаи:

2.1) $D < 0$ , откуда $a∈ (− 3;− 2)$ . Подходит.

2.2) $D = 0$ , тогда

t = −2(a+-4)2= −1 в 2(a+ 4)2

Данное $t$ дает решения $x$ , следовательно, $a = −3;−2$ не подходит.

2.3) $D > 0$ . Тогда уравнение имеет два корня и нужно, чтобы они не принадлежали промежутку $[−2;0]$ . Засчет того, что вершина параболы $tв = −1$ , то может быть единственный вариант: один корень $< −2$ , второй $> 0$ (отпадает случай, когда оба $> 0$ , и случай, когда оба $< −2$ ). Рассмотрим параболу:

$PIC$

Положение точек задается следующей системой:

({ y(− 2)< 0 ⇔ a< − 10 ( y(0) <0 3

Пересечем это с условием дискриминанта и получим $a ∈ (− ∞;− 10) 3$ .

Ответ:

$( 10) a ∈ −∞; − 3 ∪(−3;−2)$

Ошибка.
Попробуйте повторить позже

Задача 11#37054

Найдите $a$ , при которых уравнение

2(--2x-) ( -2x--) 2 log2 1 +x2 +2(a− 1)log2 1+ x2 + a − a − 2 =0

имеет решения.

Показать ответ и решение

Заметим, что по ОДЗ $x⁄= 0$ . При всех остальных $x$ аргумент логарифмов равен

--2-- 1x + x

Так как $x+ 1x$ – сумма двух взаимно обратных чисел, которая по модулю $≥ 2$ , то

| | 0< |||-2--|||≤1 |x + 1x|

В виду того, что это выражение не может быть отрицательным, так как находится в аргументе логарифма, заключаем, что

2 0 < x+-1≤ 1 ⇒ x> 0 x

Сделаем замену $( ) --2-- t= log2 x + 1x$ , следовательно, $t∈(−∞; 0]$ . Уравнение приобретает вид

2 2 t+ 2(a − 1)t+a − a− 2= 0

$D= 4(a2 − 2a+ 1)− 4(a2− a− 2)= 4(−a +3)$ . Чтобы уравнение имело решения (только тогда могут быть решения относительно $x$ ), нужно, чтобы $D ≥ 0$ , откуда $a≤ 3$ .

1) Рассмотрим случай $a= 3$ отдельно. Тогда единственный корень уравнения равен

t= −-2(a−-1)= 1− a = −2 2

Данный корень $t$ дает корень $x$ . Следовательно, это $a$ нам подходит.

2) Пусть $a < 3$ . Тогда у уравнения два корня и нужно, чтобы хотя бы один из них находился в промежутке $(−∞;0]$ . Пойдем от противного. Пусть ни один из корней не лежит в этом промежутке, то есть оба больше нуля. Тогда нам подходит такая парабола $y =t2+ 2(a− 1)t+ a2− a− 2$ :

$PIC$

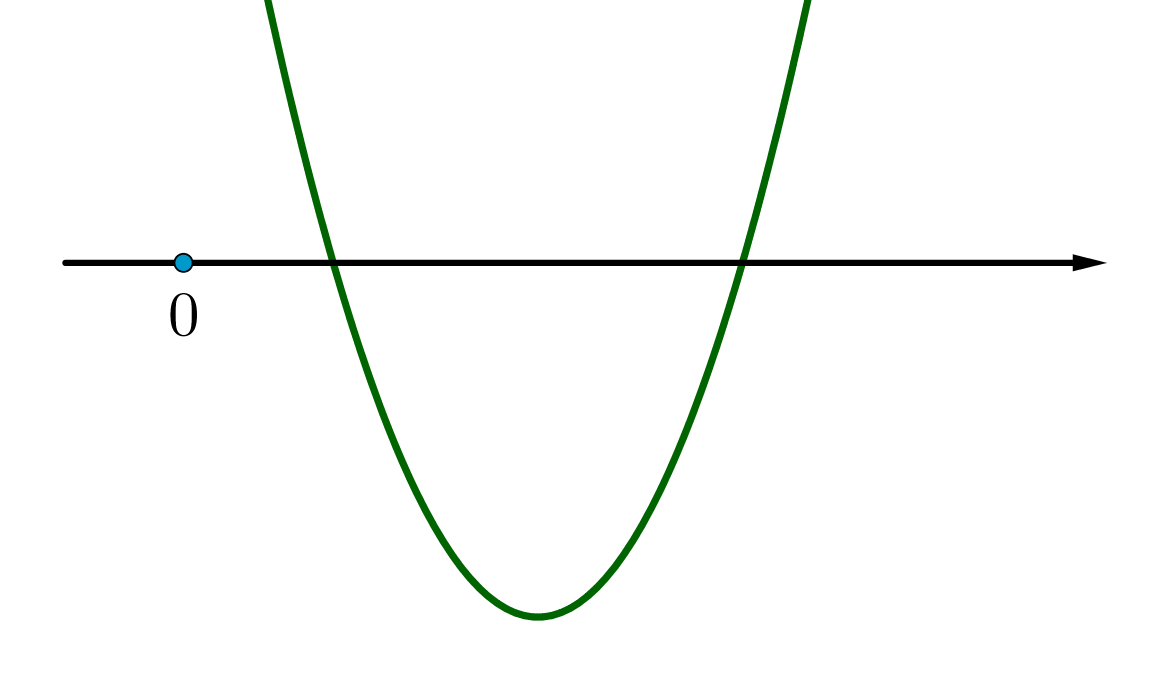
Это положение числа 0 задается следующими условиями

({ y(0)> 0 ( ⇔ a <− 1 tв >0

Следовательно, противоположные $a$ соответствуют тому, когда хотя бы один корень из промежутка $(−∞; 0]$ , то есть это $a ≥−1$ . Пересечем с дискриминантом и получим $a ∈[−1;3)$ . Также ранее нам подошло $a= 3$ . Следовательно, ответ: $a ∈[−1;3]$ .

Ответ:

$a ∈[−1;3]$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#37053

Найдите все $a$ , при которых уравнение

2 2 (log2(x+ 1)− log2(x− 1)) − 2(log2(x+ 1)− log2(x− 1))− a + 1= 0

имеет ровно два различных корня.

Показать ответ и решение

Сделаем замену $t=log(x+ 1)− log(x− 1) 2 2$ . Тогда уравнение примет вид

2 2 2 2 t − 2t+ 1= a ⇔ (t− 1) = a ⇔ t= 1± a

Исследуем, при каких значениях переменной $t$ какое число решений для переменной $x$ мы получаем. Для этого решим уравнение:

t= log (x+ 1)− log (x− 1) ⇔ (x +21 2 |{x-− 1 =2t |( ⇔ x> 1 (|{(2t− 1)x= 2t+1 |(x> 1

При $2t− 1= 0$ , откуда $t= 0$ , получаем уравнение $0⋅x =2$ , которое не имеет решений. При $t⁄= 0$ имеем единственный корень

t x= 2t+1- 2 − 1

Следовательно, исходное уравнение будет иметь два решения, когда уравнение с заменой имеет два корня $t1 ⁄=t2$ , то есть при $1+ a⁄= 1− a$ , каждый из которых удовлетворяет условию

2t+-1 2t− 1 > 1 ⇔ t> 0

Следовательно,

( { 1±a >0 ⇔ −1< a< 0; 0< a< 1 ( 1+a ⁄=1 − a

Ответ:

$a ∈(−1;0)∪ (0;1)$

Ошибка.
Попробуйте повторить позже

Задача 13#37052

Найдите все значения $a$ , при которых неравенство

(∘ ---2- ) (∘ ---2- ) loga 1− x +1 + loga 1− x +7 < 1

справедливо для каждого допустимого $x$ ?

Показать ответ и решение

Сделаем замену $t= √1−-x2+1$ . Исследуем ее. Так как $x2 ≥ 0$ , то $1− x2 ≤1$ . Тогда $0≤ √1-− x2 ≤ 1$ , а $1 ≤t≤ 2$ .

При $t= 1$ имеем два корня $x$ , при $1< t≤2$ имеем один корень $x$ . При остальных $t$ не имеем корней $x$ .

Чтобы неравенство было справедливо для любого допустимого $x$ , нужно, чтобы решение неравенства с $t$

loga t+ loga(t+6)< 1

содержало в себе множество $[1;2]$ . Преобразуем неравенство, учитывая, что $t≥ 1$

2 2 loga(t +6t)<1 ⇔ (a− 1)(t + 6t− a)< 0

Заметим, что $0< a< 1;a > 1$ .

Дискриминант: $D = (a− 1)2(36+ 4a)$ .

Рассмотрим параболу $2 y =(a− 1)(t +6t− a)$ и варианты ответа для неравенства $y < 0$ :

$PIC$

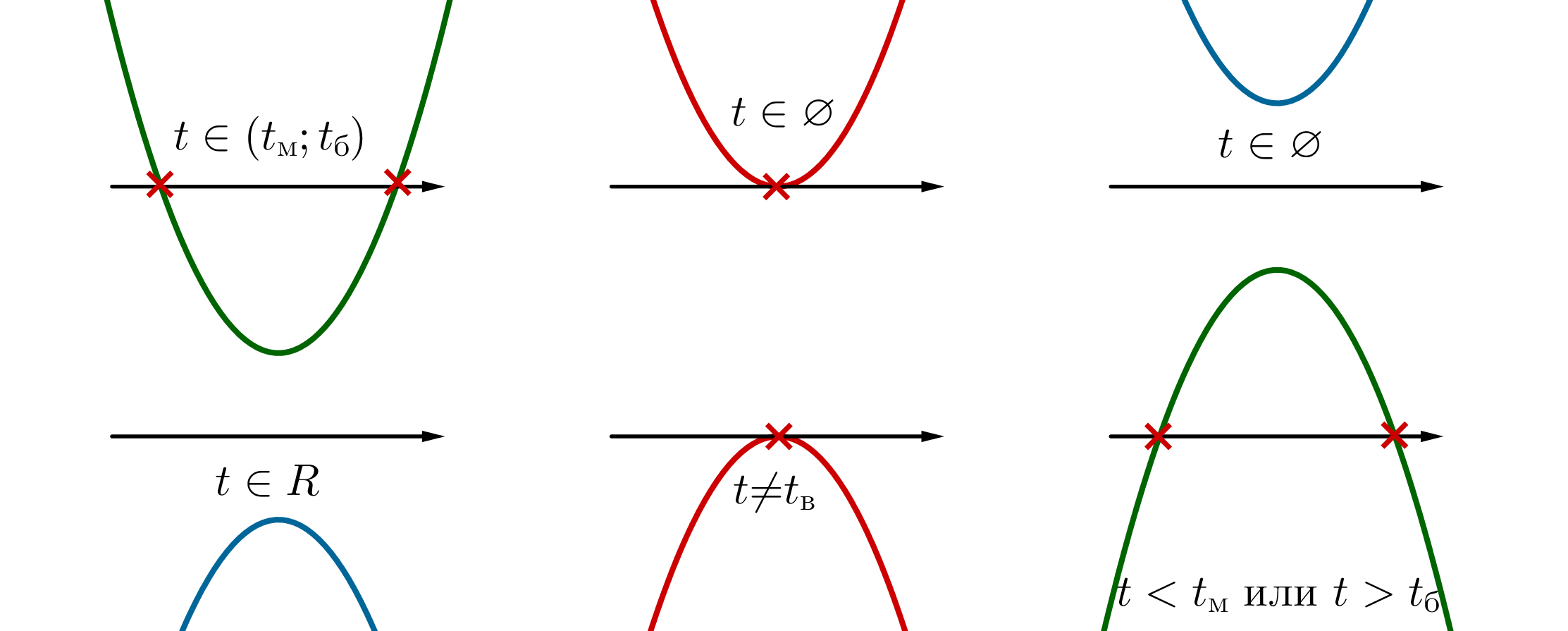
Имеет смысл рассматривать только первую верхнюю, а также все три нижние.

1) $a> 1$ . Тогда нужно, чтобы числа 1 и 2 лежали в $III$ месте, следовательно,

( |||{ y(1)< 0 | y(2)< 0 ⇔ a> 16 ||( a− 1> 0

Заметим, что для параболы с ветвями вверх условие на дискриминант необязательно, когда есть хотя бы одна точка, в которой значение функции отрицательно.

2) Левая нижняя картинка.

({ D < 0 ⇔ a ∈∅ (0< a< 1

3) Средняя нижняя картинка. $D= 0$ и $0< a< 1$ , следовательно, $a= −9;1$ . Уже невозможно.

4) Правая нижняя картинка. $D >0$ (при $a > −9$ ) и $0< a <1$ . Либо $2$ находится в $I$ месте (что невозможно, так как $tв =− 3$ ), либо $1$ находится в $V$ месте. Это задается следующими условиями

y(1)> 0 ⇔ a< 7 ⇒ 0< a< 1

Объединим все полученные значения: $a ∈(0;1)∪ (16;+∞)$ .

Расшифровка:
$I$ – до левого корня,
$II$ – в левом корне,
$III$ – между корнями,
$IV$ – в правом корне,
$V$ – правее правого корня.

Ответ:

$a ∈(0;1)∪(16;+ ∞)$

Ошибка.
Попробуйте повторить позже

Задача 14#37051

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 2 (log8(x+ a)− log8(x− a)) − 12a(log8(x+ a)− log8(x− a))+ 35a − 6a− 9= 0

имеет ровно два различных решения.

Показать ответ и решение

Воспользуемся формулой разности логарифмов и приведем уравнение к виду

( x +a)2 ( x+a ) log8x-− a − 12a⋅ log8 x− a + 35a2− 6a− 9= 0,

причем мы имеем ограничение $x> a$ и $x> −a$ , что можно записать в виде одного неравенства $x> |a|$ .

Сделаем замену $t= log8 xx+−aa$ и исследуем новую переменную. Для этого введем еще одну промежуточную неизвестную

y = x+a-= x−-a+-2a-= 1+ -2a- x− a x− a x− a

Тогда имеем следующее:

t=logy; y > 0, y = 1+-2a-, x> |a| 8 x− a

Так как функция $y = y(x)$ – обратная пропорциональность (за исключением случая $a= 0$ , который мы сейчас рассмотрим отдельно), то есть $y = y(x)$ – строго монотонная, то каждому значению $x$ соответствует не более одного $y$ . Функция $t= t(y)$ также является строго монотонной, поэтому каждому $y$ будет соответствовать не более одного $t$ . Причем можно дополнить: различным $x$ соответствуют различные $y$ , а различным $y$ – различные $t$ .

Рассмотрим случаи $a> 0$ , $a= 0$ и $a <0$ :

$a >0$ , тогда $x> a> 0$ , график $y = 1+-2a- x−a$ представляет собой убывающую гиперболу, расположенную в 1 и 3 четвертях (относительно своих асимптот), а асимптотами у нее являются $y = 1$ и $x = a$ . Следовательно, значениям $x> a$ соответствуют $y > 1$ , а им в свою очередь соответствуют $t> 0$ .
$a <0$ , тогда $x >− a> 0$ , график $y =1+ -2a x−a$ представляет собой возрастающую гиперболу, расположенную в 2 и 4 четвертях (относительно своих асимптот), а асимптотами у нее являются $y =1$ и $x= a< 0$ . Следовательно, значениям $x >− a$ соответствуют $0 <y <1$ , а им в свою очередь соответствуют $t< 0$ .
$a =0$ , тогда $x> 0$ , $x y = x ≡1$ при $x> 0$ . Значению $y = 1$ соответствует $t= 0$ .

Новое уравнение с $t$ является квадратным, то есть может иметь от нуля до двух корней:

t2− 12at+35a2− 6a− 9 =0 (∗)

Мы ищем те $a$ , при которых исходное уравнение имеет два решения, значит, если это $a= a0 > 0$ , то при нем уравнение $(∗)$ должно иметь два положительных корня. Если это $a= a0 < 0$ , то при нем должно быть два отрицательных корня. А если $a= 0$ , то $t= 0$ точно должно являться решением (есть другие решения или нет и какие они – нам неважно).

Заметим, что можно преобразовать:

(t− 6a)2 = (a+ 3)2 ⇔ t∈{7a+ 3;5a− 3}

Найденные корни совпадают при $a= −3$ и равны $t= −18$ . Поэтому это значение параметра нужно исключить. При $a⁄= −3$ нам подходят $a$ , получаемые из

⌊( ||||{ a> 0 || 7a +3 >0 ||||||( 5a − 3 >0 ||( ||||||{ a< 0 || 7a +3 <0 ||||||( 5a − 3 <0 ||( ||⌈{ a= 0 ( (7a+ 3)(5a− 3) =0

Ответ:

$a ∈(−∞;− 3)∪ (−3;− 3)∪(3;+∞ ) 7 5$

Ошибка.
Попробуйте повторить позже

Задача 15#37049

Найдите все $a,$ при которых уравнение

2( x+ a) ( x+ a) 2 log8 x−-a- − 12log8 x−-a- +35a − 6a− 9= 0

имеет ровно два различных решения.

Показать ответ и решение

Сделаем замену $x+a t= log8x−a.$ Исследуем ее. Представим, что мы решаем это уравнение относительно $x.$ Тогда имеем:

x +a t x-− a-= 8 t t x+ a =8 x− a⋅8 , x ⁄=a t t x(1− 8)= − a(1+ 8 ), x⁄= a

При $t= 0$ получаем

x⋅0 = 2a, x⁄= a

Отсюда имеем:

a = 0 ⇒ x∈ R, x⁄= 0 a⁄= 0 ⇒ x ∈ ∅

Оба варианта нам не подходят.

При $t⁄= 0$ получаем

t x = −a1-+8t, x ⁄= a 1 − 8

Отсюда имеем:

− a1+-8t⁄= a 1− 8t ( 1+ 8t) a 1 + 1−-8t ⁄= 0 a ⋅--2-t ⁄= 0 1− 8 a ⁄= 0

Запишем уравнение относительно переменной $t:$

t2− 12t+ 35a2 − 6a − 9 = 0

Оно должно иметь два решения, не равных нулю. Следовательно,

( |{D > 0 | 2 (35a − 6a− 9⁄= 0

Тогда исходное уравнение имеет ровно два различных решения при

(3 − 12√11- 3) ( 3 ) ( 3) (3 3+ 12√11-) a∈ ----35----;−7 ∪ −7;0 ∪ 0;5 ∪ 5 ;---35----

Ответ:

$( 3−12√11 3) ( 3 ) ( 3) (3 3+12√11) a ∈ 35 ;− 7 ∪ −7;0 ∪ 0;5 ∪ 5; 35$

Ошибка.
Попробуйте повторить позже

Задача 16#37048

Найдите все $a,$ при которых уравнение

2 2 2 (a− 1)cosx − (a + a− 2)cosx+ 2a − 4a+ 2= 0

имеет более одного решения на отрезке $[ 4π] 0;3 .$

Показать ответ и решение

Сделаем замену $t= cosx,$ $|t|≤ 1.$

Тогда уравнение примет вид

(a− 1)t2− (a2+ a− 2)t+ 2a2− 4a+ 2= 0 (a− 1)t2− (a − 1)(a+ 2)t+ 2(a− 1)2 = 0 (∗)

Пусть $t0$ — решение этого уравнения. Тогда после обратной замены получим уравнение $t0 = cosx.$

Заметим, что $4π cos 3 = −0,5.$ Следовательно, если $− 1< t0 ≤ −0,5,$ то уравнение имеет 2 решения на указанном в условии отрезке. Если $t0 =− 1$ или $− 0,5< t0 ≤ 1$ — то одно решение на указанном в условии отрезке. При остальных $t0$ решений не будет.

Уравнение $(∗)$ при $a= 1$ линейное, при остальных $a$ — квадратное. Рассмотрим эти два варианта по отдельности.

1) $a= 1.$ Тогда уравнение примет вид $0 = 0.$ Решениями такого уравнения являются все $t∈ℝ.$ То есть мы получаем бесконечно много значений для $t,$ следовательно, бесконечно много значений для $x.$ Такое значение параметра нам подходит.

2) $a⁄= 1.$ Заметим, что уравнение можно переписать в виде

2 (a − 1)t − (a − 1)(a+ 2)t+ (a− 1)(2a− 2)= 0

Так как $a⁄= 1,$ то можно разделить обе части равенства на $a− 1:$

2 t − (a+ 2)t+ 2a − 2= 0 (∗∗)

Дискриминант этого уравнения $D = (a− 2)2 +8 > 0$ для любого $a.$ Следовательно, уравнение $(∗∗)$ имеет два различных корня $t1$ и $t2.$

Вспомним еще раз, что для отрезка $[ ] 0; 4π3 :$

каждому $t∈ (− 1;− 0,5]$ соответствует два значения $x;$

каждому $t∈ (− 0,5;1]∪ {−1}$ соответствует одно значение $x;$

каждому $t ∕∈ [−1;1]$ не соответствует ни одно значение $x.$

Чтобы исходное уравнение имело два и больше решений на отрезке $[ 4π] 0; 3 ,$ необходимо выполнение одного из случаев:

$∙$ $− 1< t1 ≤ −0,5,$ а $t2$ — любое число;

$∙$ $− 0,5< t1 ≤ 1$ или $t1 = −1,$ $− 0,5< t2 ≤ 1$ или $t2 = −1.$

Рассмотрим функцию

y = t2− (a+ 2)t+ 2a− 2

Ее график — парабола, ветви которой направлены вверх и которая пересекает ось абсцисс в двух точках.

Случай 1.

$− 1< t1 ≤ −0,5,$ а $t2$ — любое число.

Тогда подходящие нам картинки выглядят так:

$−−10,5$ $−−10,5$

Рис. 1

Рис. 1: когда $t 1$ — это левая точка пересечения параболы с осью абсцисс. Тогда число -1 должно находиться левее левого корня, а -0,5 — либо находиться между корнями, возможно совпадая с ними, либо находиться правее правого корня.

$−−10,5$ $−−10,5$

Рис. 2

Рис. 2: когда $t1$ — это правая точка пересечения параболы с осью абсцисс. Тогда -1 должно находиться либо левее левого корня, либо между корнями, возможно, совпадая с ними, а -0,5 — совпадать с правым корнем или быть правее него.

Опишем в виде равенств/неравенств эти рисунки.

Рис. 1:

⌊( |{ y(− 1) >0 || |||( y(− 0,5)≤ 0 |||(| |||||{ y(− 1) >0 || y(− 0,5)> 0 |⌈|||| ( −1< tв < −0,5

Рис.2:

⌊( |{ y(− 1) <0 |||| ||( y(− 0,5)≥ 0 ||(|| y(− 1) ≥0 ||||{ |||| y(− 0,5)≥ 0 ⌈|||( −1< tв < −0,5

Получаем для обоих рисунков:

⌊( |{ y(− 1)> 0 |||| ||( y(− 0,5)≤ 0 ||(|| y(− 1)> 0 ||||{ ⌊ y(−0,5) |||| y(− 0,5)> 0 | -y(−-1) ≤0 (первая и третья системы вм есте) |||||( || ( ||( −1 <tв < − 0,5 ⇔ ||| ||||y(−1)≥ 0 |||{ y(− 1)< 0 || { || |⌈ |||y(−0,5)≥ 0 ||||( y(− 0,5)≥ 0 |(− 1< tв < −0,5 ||(| y(− 1)≥ 0 |||||{ || y(− 0,5)≥ 0 |⌈||||( −1 <tв < − 0,5

Далее имеем:

y(− 1)= 3a + 1, y(− 0,5)= 10a−-3, tв = a-+-2 4 2

Тогда для обоих рисунков получаем следующие значения параметра:

1 3 − 3 < a≤ 10

Случай 2.

$− 0,5 < t1 ≤1$ или $t1 = − 1,$ $− 0,5 < t2 ≤ 1$ или $t2 = − 1.$ Тогда подходящие нам картинки выглядят так:

$1−0,5$

Рис. 3

Рис. 3: -0,5 находится левее левого корня, 1 совпадает с правым корнем или находится правее него:

(|y(−0,5)> 0 |||{ − 0,5< tв < 1 ⇒ a ∈∅ ||||( y(1)≥ 0

$1−−01,5$

Рис. 4

Рис. 4: -1 совпадает с левым корнем, -0,5 находится между корнями, 1 совпадает с правым корнем или находится правее него:

( || y(−1)= 0 ||{ | y(−0,5)< 0 ⇒ a ∈ ∅ |||( y(1)≥ 0

Тогда исходное уравнение имеет более одного решения на указанном отрезке при

( ] a ∈ − 1;-3 ∪{1} 3 10

Ответ:

$( 1 -3] a ∈ −3;10 ∪{1}$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование (некоторые переходы не расписаны) или не рассмотрен случай $a= 1$	3

Верно наложены все условия для того, чтобы выполнялось условие задания	2

Рассмотрен случай $a= 1$ и/или верное введение новой переменной и её исследование	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#37047

Найдите все значения параметра $a,$ при каждом из которых уравнение

2 2 2 2 2 2 (x − 2(a+ 1)x +a +2a) + (a+ 5)(x − 2(a +1)x+ a + 2a)− a − 7a − 10 = 0

имеет

а) единственное решение;

б) ровно два различных решения.

Показать ответ и решение

Сделаем замену

2 2 2 t =x − 2(a+ 1)x+ a + 2a= (x− (a +1)) − 1

Тогда уравнение равносильно

2 2 t + (a+ 5)t− a − 7a− 10= 0

При $t> −1$ имеем два корня $x,$ при $t= −1$ имеем один корень $x,$ при $t <− 1$ корней нет.

а) Чтобы у исходного уравнения было одно решение, нужно, чтобы $D = 0$ и корень был равен -1 или $D >0$ и один корень равен -1, а второй меньше -1.

б) Чтобы у исходного уравнения было ровно два решения, нужно, чтобы $D =0$ и корень был больше -1 или $D > 0$ и один корень больше -1, а второй меньше -1.

Вычислим дискриминант и найдем его нули:

D = (a+ 5)2+ 4(a2+ 7a+ 10) =5a2+ 38a+ 65= 0 a = −5; − 13 5

Если $D = 0,$ то единственный корень $xв = − a+5. 2$ При $a =− 5$ имеем $xв = 0,$ при $a= − 13- 5$ имеем $xв = − 6. 5$ Тогда для пункта а) не подходит ни одно из найденных значений параметра, для пункта б) подходит $a= − 5.$

Если $D > 0,$ то имеем:

( 13 ) a ∈(−∞; −5)∪ − 5-;+ ∞

Для пункта а) число -1 должно находиться в $IV$ месте, то есть

( ( { y(− 1)= 0 {1 − (a+ 5)− a2− 7a− 10= 0 ( ⇔ ( a+5 xв < −1 − -2-< − 1

Отсюда получаем $√- a= − 4+ 2.$

Для пункта б) число -1 должно находиться в $III$ месте, то есть

y(− 1)< 0 ⇔ 1− (a+ 5)− a2− 7a− 10< 0

Отсюда получаем

√ - √ - a∈ (−∞; −4− 2)∪ (−4+ 2;+ ∞)

Объединяя все значения параметра, получаем

а) $a= − 4+ √2;$

б) $√ - √ - a∈ (−∞; −4− 2)∪{−5} ∪(−4+ 2;+ ∞).$

Расшифровка:

$I$ — левее левого корня,

$II$ — в левом корне,

$III$ — между корнями,

$IV$ — в правом корне,

$V$ — правее правого корня.

Ответ:

a) $√ - a = −4+ 2$

b) $√ - √ - a ∈(−∞; −4− 2)∪{− 5} ∪(−4 + 2;+ ∞ )$

Ошибка.
Попробуйте повторить позже

Задача 18#2556

Найдите все значения параметра $a,$ при каждом из которых уравнение

| 2 | 2 |cos x+ 2sinx − 2a|= cos x+ sinx +2a

имеет на промежутке $[ π- ) − 2;0$ единственный корень.

Показать ответ и решение

Так как $cos2x =1 − sin2x,$ то уравнение равносильно

2 2 |1 − sin x+ 2sinx − 2a|= 1− sin x + sinx+ 2a

Сделаем замену $t =sinx.$ Тогда если нам было нужно, чтобы уравнение имело один корень $x$ на промежутке $[− π-;0) , 2$ то новое уравнение должно иметь один корень $t$ на промежутке $[− 1;0).$

После замены имеем:

|1− t2+ 2t− 2a|= 1− t2+ t+2a ⇔

( ( |||t2− t− 1− 2a≤ 0 (∗) |{ 1[− t2 +t+ 2a ≥0 |||{⌊t1 = 4a ⇔ 1− t2+2t− 2a= 1 − t2+ t+ 2a ⇔ || 1 |( 1− t2+2t− 2a= − (1 − t2+ t+ 2a) |||||⌈t2 = − 2 ||( t3 = 2

Заметим, что корень $t3$ не удовлетворяет условию, то есть не лежит в промежутке $[− 1;0).$ Следовательно, для того, чтобы уравнение имело один корень на $[−1;0),$ нужно выполнение одного из случаев:

1) корень $t2$ подходит и корень $t1$ не подходит или совпадает с $t2;$

2) корень $t1$ подходит и корень $t2$ не подходит.

Рассмотрим эти случаи.

1) Чтобы подходил $t2,$ он должен удовлетворять неравенству $(∗).$ Чтобы не подходил $t1,$ он должен либо не принадлежать $[−1;0),$ либо совпадать с $t2,$ либо не удовлетворять неравенству $(∗).$

Таким образом, получаем систему

(|| 1 + 1− 1− 2a≤ 0 |||| 4⌊ 2 |||| 4a< − 1 { } { ||4a≥ 0 ⇔ a ∈ − 1 ∪ [0;+∞ ) ||| || 1 8 ||||| ||4a= − 2 ||( ⌈ 2 16a − 4a − 1− 2a > 0

2) Чтобы подходил $t1,$ он должен принадлежать $[− 1;0)$ и удовлетворять неравенству $(∗).$ Чтобы не подходил $t2,$ он должен не удовлетворять неравенству $(∗)$ и не совпадать с $t1.$

Таким образом, получаем систему

( |||| −12≤4a < 0 ||{ 16a − 6a − 1 ≤ 0 | 1 + 1− 1− 2a> 0 ⇔ a ∈∅ ||||| 4 2 1 ( 4a⁄= − 2

Объединяя случаи, получаем окончательно

{ 1} a∈ − 8 ∪[0;+ ∞)

Ответ:

${ 1} a ∈ −8 ∪ [0;+∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Не рассмотрен случай совпадения корней, из-за чего ответ может отличаться от верного невключением $1 a= −8$	3

Найдены все корни полученных уравнений и верно составлены неравенства для выполнения условия задания, но либо решение не завершено, либо решение содержит ошибку	2

Выполнен верный переход к совокупности двух уравнений с учетом ограничения на правую часть данного уравнения и с помощью верных преобразований получены два квадратных уравнения относительно новой переменной, например, $t$ и указаны ее допустимые значения	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 19#2445

Найдите все значения параметра $a,$ при каждом из которых уравнение

4 2 cos x − (a− 2)cosx − 3(a+ 1)= 0

имеет решение.

Показать ответ и решение

Данное уравнение с помощью замены $cos2x = t$ сводится к квадратному:

2 t− (a− 2)t− 3(a+ 1)= 0 (∗)

Далее заметим, что

−1 ≤cosx ≤1 ⇒ 0 ≤ t≤ 1

Найдем значения $a,$ при которых уравнение $(∗)$ не имеет решений либо имеет решения $t∈∕[0;1].$ Тогда все остальные значения $a$ пойдут в ответ.

Рассмотрим функцию

y = t2 − (a− 2)t− 3(a+ 1)

Для выполнения условий выше ее график — парабола с ветвями вверх — должна выглядеть, как на одной из картинок:

$PIC$

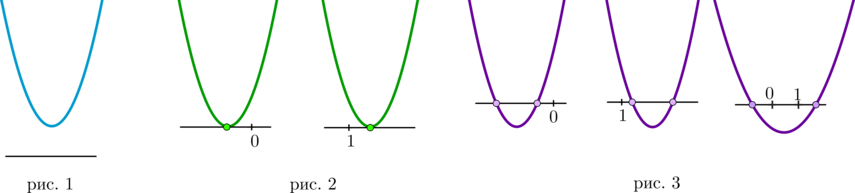
Рис. 1: $D < 0,$ уравнение не имеет корней;

Рис. 2: $D = 0,$ уравнение имеет один корень $t= a−22,$ который находится либо левее 0, либо правее 1;

Рис. 3: $D > 0,$ уравнение имеет два корня, причем либо оба корня находятся левее 0, либо оба корня находятся правее 1, либо один корень левее 0, а другой корень правее 1.

Все эти случаи записываются в совокупность

⌊ D < 0 || (||D = 0 || |{⌊ a−-2 ||| ||⌈ 2 < 0 || |( a−-2> 1 || ( 2 ⌊ || ||{D > 0a − 2 |a ∈∅ || |tв =--2- < 0 ||a = −4 ||| |(y(0)> 0 ⇔ ||a ∈(−∞; −4)∪ (−4;−1) || ( |⌈a ∈∅ || ||{D > 0a − 2 a ∈(0;+∞ ) || |tв =--2- > 1 ||| |(y(1)> 0 || ( || |{D > 0 ⌈ |(y(0)< 0 y(1)< 0

Здесь $tв$ — абсцисса вершины параболы, дискриминант $2 D =(a+ 4) .$

Решив данную совокупность, получим

a∈ (−∞;− 1)∪(0;+∞ )

Следовательно, исходное уравнение имеет решение при

−1 ≤a ≤ 0

Замечание.

По теореме Виета корнями квадратного уравнения

t2− (a− 2)t− 3(a+ 1)= 0

являются $t1 = −3$ и $t2 = a +1.$

Тогда с учетом ограничения $0 ≤ t≤ 1$ исходное уравнение имеет решение, если $0 ≤a + 1≤ 1.$ Отсюда получаем тот же ответ $− 1≤ a ≤0.$

Ответ:

$a ∈[−1;0]$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Необоснованы переходы по ходу исследования	3

Верно наложены все условия для существования решений уравнения, но либо есть ошибка, либо решение не завершено	2

Верно введена и исследована замена, рассмотрена квадратичная функция	1
ИЛИ
Верно найдены корни квадратного уравнения

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 20#1189

Найдите все значения параметра $a,$ при каждом из которых уравнение

x x 2 √----- (4 − 3⋅2 + 3a− a )⋅ 2− x = 0

имеет ровно два различных корня.

Показать ответ и решение

Заметим, что уравнение всегда имеет как минимум один корень $x =2.$

Заметим, что корни уравнения должны удовлетворять условию $2 − x ≥ 0.$

Решим уравнение $4x− 3⋅2x+ 3a− a2 = 0.$ Если сделать замену $2x = t,$ причем $t> 0,$ то уравнение примет вид $t2− 3t+ a(3− a)= 0.$ По теореме Виета корнями (необязательно различными) будут $t1 = a$ и $t2 = 3− a.$

То есть $2x = a$ и $2x = 3− a.$ Заметим, что если, например, $a≤ 0,$ то уравнение $2x = a$ не имеет решений. В противном случае оно будет иметь решение $x = log2a.$

Число $x = 2$ будет являться решением уравнений $2x = a$ или $2x = 3 − a,$ если $a= 4$ или $3− a= 4$ соотвественно.

Таким образом, исходное уравнение

(4x− 3⋅2x+ 3a− a2)⋅√2−-x-= 0

будет иметь два различных корня в следующих двух случаях.

1) $a⁄= 3 − a.$ Тогда либо один из корней $a$ или $3 − a$ должен оказаться $≤0,$ давая противоречие с условием $t >0;$ либо один из корней $a$ или $3 − a$ должен оказаться $≥ 4,$ поскольку при $> 4$ он не будет удовлетворять условию $2 − x ≥ 0,$ а при $= 4$ будет совпадать с уже имеющимся корнем $x = 2.$ При этом другой корень должен оказаться $> 0$ и $< 4.$