Функции. Сумма взаимно обратных —Каталог задач по ЕГЭ - Математика

Тема 18. Задачи с параметром

18.18 Функции. Сумма взаимно обратных

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#33034

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 2 3 3 2 3 a (x + 1) +(x +1) = 12ax

имеет единственное решение.

Показать ответ и решение

Заметим, что $x= 0$ не является решением уравнения, поэтому разделим обе части равенства на $x3 :$

( 1 )3 1 a2 x +x + x3 +2+ x3 =12a

Сделаем замену $t= x+ 1x$ , тогда $t3 = x3+ 1x3 + 3x+ 3x$ , откуда $x3+ x13 =t3− 3t$ , следовательно,

a2t3+t3− 3t− 12a+2 =0 ⇔ (a2 +1)t3− 3t− 12a+ 2= 0

Так как $t$ представляет собой сумму взаимно обратных чисел, то $|t|≥2$ , причем $|t|= 2$ соответствует один $x$ , $|t|>2$ соответствует два $x$ . Следовательно, исходное уравнение имеет один корень в том случае, когда:

новое уравнение имеет один корень $t1$ , причем $|t1|=2$ (то есть $t2,t3$ не существуют);

новое уравнение имеет три одинаковых корня $t1 = t2 =t3$ , причем $|t1|=2$ ;

новое уравнение имеет корень $t1$ такой, что $|t1|=2$ , а другие корни $t2$ и $t3$ такие, что $|t2|< 2$ , $|t3|<2.$

1.

Пусть $t = 2 1$ . Тогда

1 8a2+ 8− 6− 12a+ 2= 0 ⇔ a= 2;1

1.1.: При $1 a = 2$ получаем уравнение $5t3− 12t− 16 =0 ⇔ (t− 2)(5t2 +10t+8)= 0$
Убеждаемся, что вторая скобка корней не имеет, следовательно, $a= 12$ нам подходит.
1.2.: При $a =1$ получаем уравнение $2t3− 3t− 10 =0 ⇔ (t− 2)(2t2 +4t+ 5) =0$
Убеждаемся, что вторая скобка корней не имеет, следовательно, $a= 1$ нам подходит.

2.

Пусть $t1 = −2$ . Тогда

− 8a2− 8+ 6− 12a+ 2= 0 ⇔ a= − 3;0 2

2.1.: При $a =− 3 2$ получаем уравнение $3 2 13t− 12t+ 80= 0 ⇔ (t+ 2)(13t − 26t+ 40) =0$
Убеждаемся, что вторая скобка корней не имеет, следовательно, $a= − 3 2$ нам подходит.
2.2.: При $a =0$ получаем уравнение $t3 − 3t+ 2= 0 ⇔ (t+2)(t− 1)2 =0$
Вторая скобка имеет корень, но он по модулю меньше $2$ , следовательно, $a= 0$ нам подходит.

Итого $a =− 32;0;12;1.$

Ответ:

$a ∈{− 3;0;1;1} 2 2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#33026

Найдите все значения параметра $a,$ при каждом из которых уравнение

4 2 3 16x + ax +1 = 32x +8x

имеет ровно три различных корня.

Показать ответ и решение

Заметим, что $x= 0$ не является корнем данного уравнения. Тогда разделим обе части на $2 4x :$

2 1 a ( 1) 4x + 4x2-+ 4 =4 2x+ 2x

Пусть $t= 2x + 12x-$ — сумма взаимно обратных чисел, следовательно, $|t|≥ 2$ и $t2 = 4x2+ 41x2-+ 2,$ тогда уравнение примет вид

t2− 2+ a= 4t ⇔ t2− 4t+ a− 2= 0 4 4

Исследуем замену.

Если $|t|=2,$ то таким значениям $t$ соответствует по одному $x.$

Если $0 ≤ |t|< 2,$ то таким $t$ не соответствует ни один $x.$

Если $|t|>2,$ то каждому такому $t$ соответствует два $x.$

Так как уравнение с новой неизвестной имеет не более двух решений, то чтобы исходное уравнение имело три решения, новое уравнение должно иметь два решения $t1$ и $t2,$ причем $|t1|>2,$ $|t2|=2.$

1.

Пусть $t2 = 2$ . Тогда

a 4− 8+ 4 − 2= 0 ⇔ a= 24

Следовательно, уравнение примет вид

t2 − 4t+ 4= 0 ⇔ t =2

Получили, что $t1 = t2 = 2.$ Этот случай нам не подходит.

2.

Пусть $t2 = −2.$ Тогда

a 4 +8 + 4 − 2= 0 ⇔ a = −40

Следовательно, уравнение примет вид

2 t− 4t− 12= 0 ⇔ t1 = 6,t2 = − 2

Получили $|t1|> 2,$ что нам подходит.

Значит, ответ $a= −40.$

Ответ:

$a ∈{− 40}$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Необоснованы переходы по ходу исследования	3

Верно наложены условия существования трех решений уравнения, но либо есть ошибка, либо решение не завершено	2

Верно введена и исследована замена	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 3#32963

Найдите все значения параметра $a$ , при каждом из которых уравнение

||x2−-4ax+4a2+-1|| 2 || x− 2a ||+x − 2x− 1= 0

имеет хотя одно решение.

Показать ответ и решение

Подмодульное выражение можно преобразовать следующим образом:

x2−-4ax+4a2+-1 (x−-2a)2+-1 --1-- x− 2a = x− 2a = (x− 2a)+ x− 2a

Следовательно, если $x − 2a= t$ , то подмодульное выражение представляет собой сумму двух взаимно обратных чисел $t$ и $1 t$ , следовательно, модуль от этой суммы $≥2$ . Получаем

|| || ||t+ 1t||= 2− (x− 1)2

Правая часть равенства $≤ 2$ , следовательно, по методу оценки равенство возможно тогда и только тогда, когда обе части равны $2$ , то есть

⌊ ( ( {x= 1 |{t+ 1 =±2 ({ x− 2a= ±1 ||| (a= 0 | t ⇒ ( ⇔ || ( (2 − (x− 1)2 = 2 x− 1= 0 |⌈ {x= 1 (a= 2

Следовательно, ответ $a= 0;2.$

Ответ:

$a ∈{0;1}$

Ошибка.
Попробуйте повторить позже

Задача 4#32970

Найдите все значения параметра $a$ , при каждом из которых неравенство

x −x |x −x | (x −x) 4 +4 + 8|2 +2 − a|+11a< 26+ 2a 2 + 2

имеет хотя бы одно решение.

Показать ответ и решение

Сделаем замену $t=2x +2−x$ , тогда $t≥2$ как сумма двух взаимно обратных положительных чисел. Тогда $t2 = 4x+ 4− x+2$ и неравенство примет вид

2 2 2 2 2 t− 2+ 8|t− a|+ 11a< 26 +2at ⇔ (t− a) + 8|t− a|− 28+11a− a < 0 ⇔ (|t− a|+4) < a − 11a+ 44

Заметим, что $a2− 11a+ 44> 0$ при всех $a∈ ℝ$ .

Рассмотрим две функции $y = y = (|t− a|+ 4)2 1$ и $y = y = a2− 11a+ 44 2$ .

$PIC$

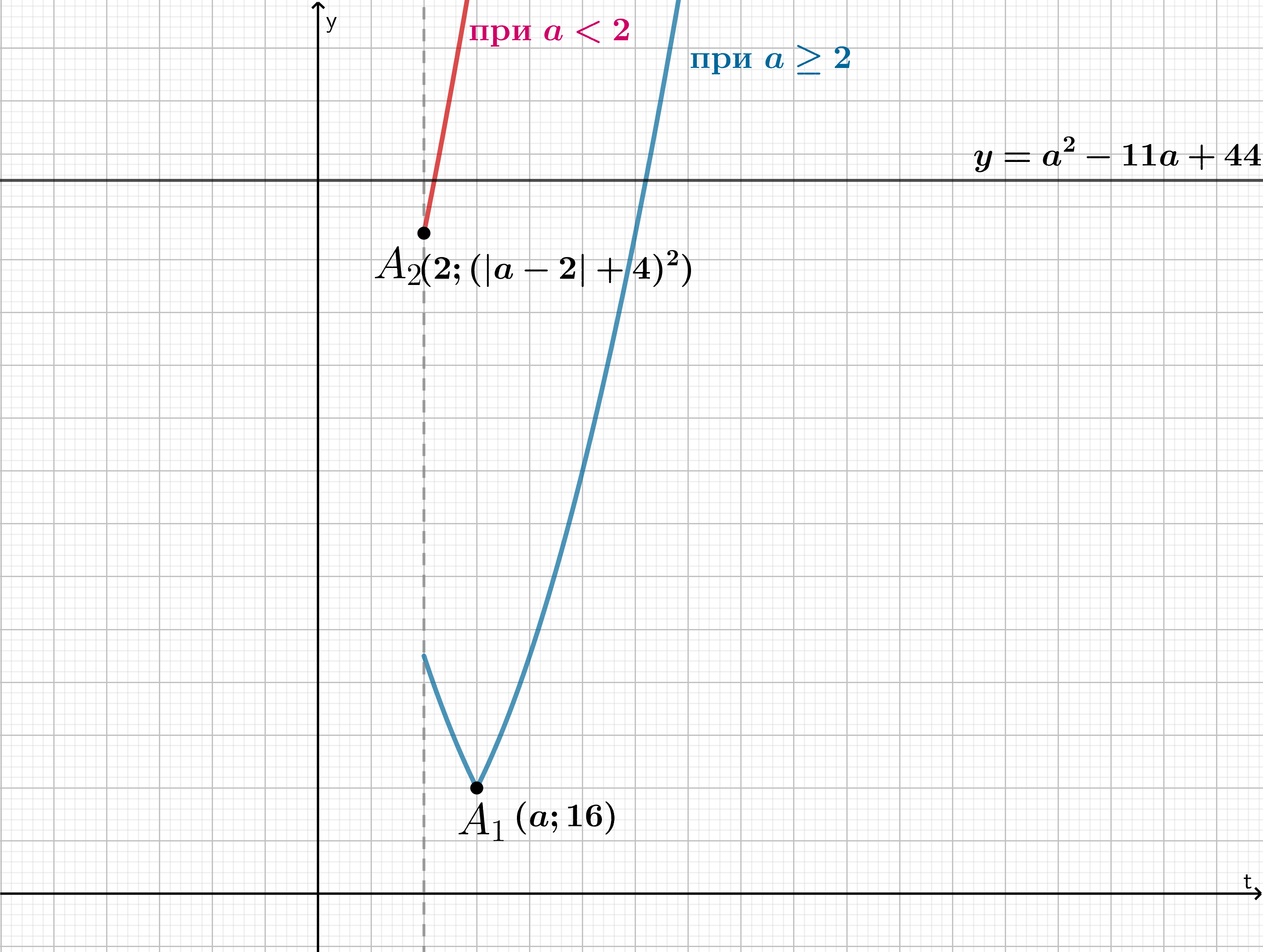
Рассмотрим случаи:

1.: $a ≥2$ . Следовательно, $A 1$ должна располагаться ниже прямой $y =y 2$ , чтобы неравенство имело решения. Значит, ее ордината должна быть меньше числа $2 a − 11a+ 44$ : $⌊ 16 <a2− 11a+44 ⇔ a2− 11a+ 28> 0 ⇒ ⌈ a> 7 2≤a <4$
2.: $a <2$ . Следовательно, $A1$ должна располагаться ниже прямой $y = y2$ , чтобы неравенство имело решения, то есть $y1(2)< y1$ , значит, $(|a − 2|+4)2 < a2− 11a+ 44 ⇔ 8|a − 2|< 24− 7a ⇔ (|{ 8 7a− 24< 8(a− 2)< 24 − 7a ⇔ a< 3 ⇒ −8< a< 2 |(a> −8$

Следовательно, $− 8< a< 4$ и $a >7.$

Ответ:

$a ∈(−8;4)∪ (7;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 5#32964

Найдите наибольшее значение параметра $a$ , при котором неравенство

√- 2 ---√a---- √4-3|| (πx )|| a a(x − 2x+ 1)+ x2− 2x+ 1 ≤ a ⋅|sin 2 |

имеет хотя бы одно решение.

Показать ответ и решение

Если сделать замену $t= √a(x− 1)2 > 0$ , то неравенство (определенное при $a≥ 0$ ) равносильно

√4-( 1) || (πx)|| a t+ t ≤|sin 2 |

Скобка представляет собой сумму взаимно обратных положительных чисел, следовательно, $≥ 2$ . Тогда вся левая часть $√- ≥ 24a$ . Правая часть принимает значения из отрезка $[0;1]$ . Следовательно, неравенств имеет решения как минимум в том случае, если

24√a ≤1 ⇔ a≤ 1- 16

Покажем, что при $a= 116$ неравенство имеет решения. При этом $a$ обе части неравенства равны $1$ , следовательно, неравенство равносильно равенству

(||a = 116- 4√-( 1) || ( πx)|| ||{ √ - a t+ t = 1= |sin 2- | ⇔ ||t = a(x− 1)2 =1 ⇔ ||(sin(πx)= ±1 ( 2 ||||a = 116- (| 1 {x =− 1;3 ⇔ { a= 16 |||| |( x= −1;3 ( πx2-= π2 + πn,n∈ ℤ

Следовательно, $a= 116$ подходит.

Ответ:

$a ∈{-1} 16$

Ошибка.
Попробуйте повторить позже

Задача 6#32962

Найдите все значения параметра $a$ , при каждом из которых неравенство

( √-)x 4 2( √-)x 2y y+1 2 √ - 3 +2 2 + (a +6− 4a )3 − 2 2 + 2 − a ⋅2 + a − 8≤ 0

имеет хотя бы одно решение $(x;y)$ .

Показать ответ и решение

Заметим, что $(3+ 2√2)(3− 2√2)= 1$ , следовательно, $3− 2√2 =--1√- 3+2 2$ , следовательно, если $t= (3+ 2√2-)x$ , $z = 2y$ , то уравнение равносильно

4 2 1 2 2 √ - t+(a − 4a + 6)⋅t + z − 2az+ a − 2 2 |⋅t>0 ≤0 ⇔ p(t)=t2+ ((z− a)2 − 2√2)t+((a2 − 2)2+2)≤ 0

Полученное неравенство должно иметь хотя бы одно решение $(t;z)$ , где $t,z > 0.$ Относительно переменной $t$ неравенство квадратное. Заметим, что если уравнение $p(t)=0$ имеет решения, то они одного знака, так как произведение корней положительно и равно $((a2 − 2)2+2$ .

Следовательно, по свойству квадратичной функции неравенство $p(t)≤ 0$ имеет решения, если

(|| (|| 2 √ -2 2 2 |{D ≥ 0 |{((z − a) − 2 2) ≥ 4((a − 2) + 2) |||p(0) >0 ⇒ |||(a2− 2)2+ 2√> 0 ⇔ (t(верш ) >0 ((z− a)2− 2 2< 0 (|⌊ 2 √- √ - |||||⌈ (z− a) − 2√2 ≥ b√- { (z− a)2 − 2√-2 ≤− b ||||(z− a)2− 2 2< 0 ||(b= 4((a2− 2)2+ 2)

Заметим, что $√b≥ 2√2$ , то неравенство $(z − a)2− 2√2-≥√b$ нам не подходит, следовательно, система равносильна

( {(z− a)2 ≤ −√b-+2√2 (b= 4((a2− 2)2+ 2)

из $√b≥ 2√2$ следует, что $− √b+ 2√2≤ 0$ , следовательно, первое неравенство имеет решения тогда и только тогда, когда $√b= 2√2$ , следовательно, $4((a2− 2)2+ 2)=8$ , откуда $a= ±√2$ . Тогда решением неравенства будут $z = a$ . Следовательно, $z > 0$ соответствует $a =√2-$ .

Ответ:

$a ∈{√2}$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#32925

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 a a −a 2−a 2 x ⋅3 − 3 − 16x =9 ⋅3 − 3 ⋅x

имеет хотя бы одно целое решение.

Показать ответ и решение

Уравнение равносильно

2 (a −a) ( a −a) (a −a)(2 ) x 3 + 9⋅3 − 3 + 9⋅3 − 16x= 0 ⇔ 3 + 9⋅3 x − 1 = 16x

Заметим, что $x= ±1$ не является решением уравнения, следовательно, уравнение можно переписать в виде

3-(a−1 1−a) -x--- 16 3 + 3 = x2− 1

Выражение $a−1 1−a 3 +3$ представляет собой сумму двух положительных взаимно обратных чисел, следовательно, $3( ) 3 3 b= 16 3a−1+31−a ≥ 16 ⋅2= 8$ при всех $a$ . Рассмотрим функцию $b= b(x)$ в системе координат $xOb$ :

x b= x2− 1

Ее производная

2 2 b′ = 1⋅(x-−21)− x2-⋅2x-= −-x2+-12 < 0 (x − 1) (x − 1)

Следовательно, $b=b(x)$ — убывающая функция при всех $x∈ ℝ∖{±1}$ .

$x→ −1− 0$ имеем $b → −∞$ ;

$x→ −1+ 0$ имеем $b → +∞$ ;

$x→ 1− 0$ имеем $b→ − ∞$ ;

$x→ 1+ 0$ имеем $b→ + ∞;$

$x→ −∞$ имеем $b → 0− 0$ ;

$x→ +∞$ имеем $b → 0+0.$

$PIC$

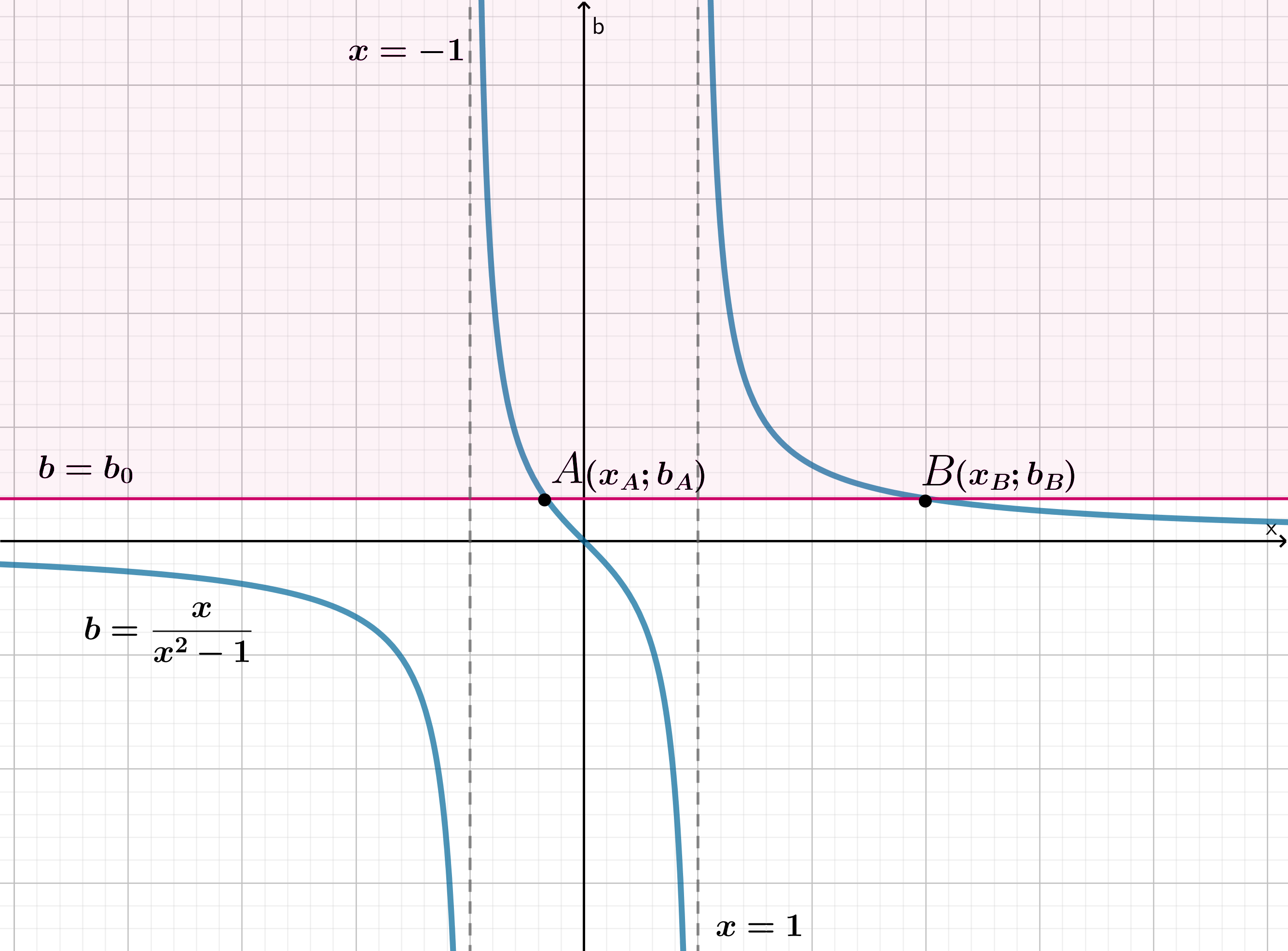
Изобразим график функции $b= b(x)$ в системе координат $xOb$ и отметим область $b≥ b0$ , где $b0 ≥ 38$ . Видим, что прямая $b= b0$ пересекает график в двух точках $A$ и $B$ . Тогда всем $b0 = b(x)$ удовлетворяют $x∈ {xA;xB}.$ Так как $xA ∈ (−1;0)$ , то $x= xA$ не является целыми решением. Следовательно, целой должна быть точка $x= xB.$

Так как $b0 ≥ 38$ , а точка на графике $b= b(x)$ и ординатой $38$ — это точка $D (3;38)$ (ищется из уравнения $x2x−1-= 38$ , $x> 0$ ), то $xB = 2;3$ . Следовательно,

(⌊ ⌊ ( ) 2 ||| 9t2− 32t+ 9= 0 ⌊ (16± 5√7) | 316 3a−1+ 31−a = 3 |{|⌈ || a= 1+ log3 ---9--- ⌈ 3-(3a−1+ 31−a)= 3 ⇒ ||| t =1 ⇒ ⌈ 16 8 |(t= 3a− 1 a= 0

Ответ:

$a ∈{0;log(16± 5√7-)− 1} 3$

Ошибка.
Попробуйте повторить позже

Задача 8#31913

Найдите все значения параметра $a,$ при каждом из которых уравнение

x x+2 −x 1−x 4 + 2 + 7= a− 4 − 2⋅2

имеет решения.

Показать ответ и решение

Уравнение равносильно

x −x ( x −x) 4 + 4 + 4 2 + 2 + 7= a

Пусть $x 2 =y.$ Тогда каждому значению $y ∈(0;+∞ )$ соответствует ровно одно значение $x ∈(−∞; +∞ ).$

Если $y + 1y = t,$ то $t∈ [2;+ ∞)$ как сумма двух взаимно обратных положительных чисел. Таким образом, каждому $t≥2$ соответствует ровно как минимум одно значение $y ∈ (0;+ ∞),$ каждому из которых соответствует ровно одно $x ∈(−∞; +∞ ).$

Тогда получаем $t2 = y2+-1+ 2 =4x +4−x +2 y2$ и уравнение примет вид

2 2 t − 2+ 4t+7 = a ⇔ (t +2) = a− 1

Если полученное уравнение имеет хотя бы одно решение $t≥ 2,$ то исходное уравнение имеет хотя бы одно решение $x.$

При $a≥ 1$ имеем $√---- t= − 2± a− 1,$ причем $√ ---- t= −2− a− 1≤ −2.$ Следовательно, нужно:

√ ---- √ ---- −2 + a− 1≥ 2 ⇔ a− 1≥ 4 ⇔ a ≥17

Это удовлетворяет условию $a ≥1.$

Ответ:

$a ∈[17;+ ∞ )$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Решение верно, получен верный ответ, но переходы по ходу исследования недостаточно обоснованы	3

Верно решено уравнение относительно новой переменной, но допущена ошибка в ходе его решения	2
ИЛИ
неверно составлено неравенство для выполнения условия задачи

Введена и исследована новая переменная	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 9#31813

Найдите все значения параметра $a$ , при каждом из которых при любом $b >0$ уравнение

(1 ) a⋅log1x−2 4= log2 x − 2 − b

имеет хотя бы одно решение, меньшее $1 3$ .

Показать ответ и решение

Пусть $log (1− 2) =y 2 x$ . Тогда имеем:

2a- b= y− y (∗)

На решение $x$ , удовлетворяющее условию задачи, наложены следующие ограничения:

( 1 |||| x − 2> 0 |{ 1 ( 1) ||| x − 2⁄= 1 ⇔ x∈ 0;3 ||( x< 1 3

При таких $x$ имеем $1− 2> 1 x$ . Так как $y = log t 2$ – возрастающая функция, то наименьшее значение она достигает при наименьшем значении аргумента, следовательно, при найденных $x$ имеем $y > log 1 =0 2$ .

Условие “У данного уравнения при любом положительном $b$ должно быть хотя бы одно решение $y >0$ ” можно переформулировать следующим образом: “Область $E(f)$ значений функции $f(y) =y− 2a y$ при $∀y > 0$ должна содержать в себе луч $(0;+∞ )$ либо совпадать с ним.”

$∙$ Если $a= 0$ , то $f(y)=y$ и $∀y >0$ имеем $(0;+∞ )⊆ E(f)$ . Все хорошо.

$∙$ Если $a< 0$ , то $c= −2a> 0$ и получим

2a √-- ( 1) f(y)= y+ y-= 2a⋅ h+ h |h=√y->0 2a

Так как $h+ 1 h$ – сумма двух взаимно обратных положительных чисел, то $h+ 1 ≥2 h$ , следовательно, $E(f)=[2√2a;+ ∞)$ . Все плохо.

$∙$ Если $a> 0$ , то функция $f(y)$ при $y > 0$ не имеет точек разрыва, то есть является непрерывной. При $y → 0+$ имеем $1 → +∞ y$ , следовательно, $f → − ∞$ . Если $y → +∞$ , то $f → + ∞$ . Следовательно, $E (f)= ℝ$ . Все хорошо. $PIC$