Четность как частный случай симметрии —Каталог задач по ЕГЭ - Математика

Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Четность как частный случай симметрии

Тема 18. Задачи с параметром

18.27 Четность как частный случай симметрии

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела задачи с параметром

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31651

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 2cosax− 3tgx − 2 =0

имеет единственное решение.

Показать ответ и решение

Заметим, что функция $f(x)= 2cosax − 3tg2x− 2$ является четной и уравнение имеет вид $f(x)= const$ . Следовательно, если уравнение имеет решение $x0 ≥0$ , то оно имеет также решение $− x0 ≤ 0$ . Значит, количество решений уравнения будет четным, если среди решений нет $x =0$ , и нечетным, если среди решений уранвения есть $x= 0$ . Так как нам требуется, чтобы уравнение имело единственное решение, что является нечетным количеством, то $x= 0$ — решение уравнения.

1.

Найдем, при каких $a$ число $x =0$ является решением уравнения:

2 2cos0− 3tg 0− 2 =0 ⇔ 0= 0 ⇔ a ∈ℝ

2.

Проверим, является ли $x =0$ единственным корнем уравнения при найденных $a$ или уравнение имеет другие корни. Для этого заметим, что если мы определим хотя бы один корень $x1 ⁄= 0$ , то найденные значения параметра нам не подойдут; если же мы докажем, что других корней нет, то найденные $a$ нам подходят. Итак, при $a∈ ℝ$ уравнение имеет вид

2 2(cos(ax)− 1)=3tg x

Левая часть уравнения $2(cos(ax)− 1)≤ 0$ , а правая часть $2 3tg x≥ 0$ , следовательно, по методу оценки равенство возможно тогда и только тогда, когда обе части равенства равны $0:$

( ( { cos(ax)= 1 { ax= 2πn, n∈ ℤ ( tgx =0 ⇔ ( x= πm, m ∈ℤ

Если $a ∈ℚ$ , то существуют такие $n,m∈ ℤ$ , что система имеет решение $x ⁄= 0 1$ . Приведем пример. Пусть $a= p q$ , $p ⁄=0$ . Возьмем $n =p$ , $m = 2q$ и получим $x =2πq$ . Если $p= 0$ , то все $x= πm$ являются решением системы.

Если $a ∕∈ℚ$ , то $x= 2πan⁄= πm$ ни при каких $n,m ∈ℤ$ , так как в противном случае $2a = mn.$

Следовательно, $a$ иррациональное.

Ответ:

$a$ – иррациональное

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#31649

Найдите все значения параметра $a$ , при каждом из которых уравнение

tg|a|= log2(cosx− |x|)

имеет единственное решение.

Показать ответ и решение

Заметим, что функция $f(x)= log (cosx− |x|) 2$ является четной и уравнение имеет вид $f(x)= const$ . Следовательно, если уравнение имеет решение $x0 ≥ 0$ , то оно имеет также решение $− x0 ≤ 0$ . Значит, количество решений уравнения будет четным, если среди решений нет $x =0$ , и нечетным, если среди решений уранвения есть $x= 0$ . Так как нам требуется, чтобы уравнение имело единственное решение, что является нечетным количеством, то $x= 0$ — решение уравнения.

1.

Найдем, при каких $a$ число $x =0$ является решением уравнения:

tg |a|= log2(cos0− |0|) ⇔ tg|a|=0

2.

log2(cosx− |x|)= 0 ⇔ cosx= 1+ |x|

Заметим, что левая часть равенства $cosx≤ 1$ , а правая $1+|x|≥1$ , следовательно, по методу оценки равенство возможно тогда и только тогда, когда обе части равны $1 :$

( { cosx= 1 ( 1+|x|=1 ⇔ x= 0

Таким образом, все $a$ , при которых $tg|a|=0$ , нам подходят. А это $a= πn, n ∈ℤ.$

Ответ:

$a ∈{πn}, n∈ ℤ$

Ошибка.
Попробуйте повторить позже

Задача 3#18305

Найдите все значения параметра $a,$ при которых уравнение

2 2 cosx − x − a =a|x|− 3

имеет ровно одно решение.

Показать ответ и решение

Преобразуем исходное уравнение:

2 2 2 2 cosx − x − a =a|x|− 3 ⇔ cosx − x − a +3 = a|x|

Пусть $2 2 f(x)= cosx− x − a + 3,$ $g(x) =a|x|.$ Заметим, что и $f(x),$ и $g(x)$ являются четными функциями. Функция $f(x)$ четна, так как это разность четных функций $y = cosx$ и $y = x2+ a2− 3.$ Функция $g(x)$ четна, так как это произведение четной функции $y =|x|$ и константы $a.$

Следовательно, если $x0$ является корнем исходного уравнения, то $− x0$ тоже является его корнем. Значит, если при некотором значении параметра $a$ исходное уравнение имеет какой-то корень, отличный от $x= 0,$ то корней хотя бы 2.

В условии нас просят найти такие значения параметра $a,$ при которых уравнение имеет ровно один корень. Следовательно, этот корень должен быть равен 0. Пусть $x= 0,$ тогда

cos(0)− 02− a2 = a⋅|0|− 3 ⇔ 1− a2 = −3 ⇔

⌊ 2 ⌈a= 2 ⇔ a = 4 ⇔ a= −2

Мы получили два значения параметра $a,$ при которых возможно такое, что исходное уравнение имеет ровно один корень. При других значениях параметра $x =0$ не является корнем, значит, при таких значениях параметра количество корней уравнения четно, что противоречит условию. Осталось проверить действительно ли при $a = 2$ и $a= −2$ уравнение имеет ровно один корень. Пусть $a= 2,$ тогда

cosx − x2− 22 +3 = 2|x| ⇔ cosx − x2 − 1 = 2|x| ⇔

⇔ cosx= |x|2+ 2|x|+ 1 ⇔ cosx= (|x|+ 1)2

Заметим, что $cosx ≤1$ при любом $x,$ а $2 (|x|+ 1) ≥ 1$ при любом $x.$ Тогда равенство возможно только если обе части равны 1, то есть

( 2 { cosx= 1 cosx= (|x|+ 1) ⇔ ( (|x|+ 1)2 =1 ⇔

({ ⇔ x= 2πn ⇔ x = 0 ( x= 0

Следовательно, при $a= 2$ исходное уравнение действительно имеет ровно один корень.

Пусть $a = −2,$ тогда

cosx− x2− (− 2)2 +3 = −2|x| ⇔ cosx− x2− 1= −2|x| ⇔

⇔ cosx= |x|2− 2|x|+ 1 ⇔ cosx= (|x|− 1)2

Заметим, что на промежутке $π [0;-2]$ косинус убывает, при этом в точке $π x = 2$ его значение равно 0, значит, в точке $x = 1$ значение косинуса больше 0.

Тогда рассмотрим функцию $y = (|x|− 1)2.$ На промежутке $[1; π2]$ она возрастает, причем в точке $x= 1$ значение этой функции равно 0, а значит, значение в точке $x = π 2$ больше 0. Тогда мы можем схематично нарисовать графики левой и правой частей уравнения на промежутке $π [0;2]:$

$PIC$

По картинке видно, что графики пересекаются на отрезке $[1; π], 2$ следовательно, при $a =− 2$ у исходного уравнения есть корень, отличный от 0. Значит, $a = −2$ нам не подходит.

Тогда исходное уравнение имеет ровно одно решение при $a = 2.$

Ответ:

$a ∈{2}$

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	4

Недостаточное обоснование либо в ходе рассмотрения функций, либо при решении уравнений	3

Верно найдены потенциальные значения параметра, но проверка не выполнена	2

Введена и верно исследована функция	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 4#2645

При каких значениях параметра $a$ уравнение

2x2 + atg(cosx) + a2 = 0

имеет единственное решение?

Показать ответ и решение

Заметим, что так как $x2$ и $cosx$ — четные функции, то если уравнение будет иметь корень $x0$ , оно также будет иметь и корень $− x0$ .
Действительно, пусть $x0$ – корень, то есть равенство $2x2+ atg(cosx0) + a2 = 0 0$ верно. Подставим $− x0$ : $2 2 2 2 2(− x0) + atg(cos(− x0)) + a = 2x0 + atg(cos x0) + a = 0$ .

Таким образом, если $x0 ⁄= 0$ , то уравнение уже будет иметь как минимум два корня. Следовательно, $x0 = 0$ . Тогда:

[ 2 ⋅ 0 + atg(cos 0) + a2 = 0 ⇒ a2 + atg1 = 0 ⇒ a = 0 a = − tg1

Мы получили два значения параметра $a$ . Заметим, что мы использовали то, что $x = 0$ точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра $a$ в исходное уравнение и проверить, при каких именно $a$ корень $x = 0$ действительно будет единственным.

1) Если $a = 0$ , то уравнение примет вид $2x2 = 0$ . Очевидно, что это уравнение имеет лишь один корень $x = 0$ . Следовательно, значение $a = 0$ нам подходит.

2) Если $a = − tg1$ , то уравнение примет вид

2x2 − tg1 ⋅ tg(cosx) + tg21 = 0

Перепишем уравнение в виде

2x2 + tg21 = tg1 ⋅ tg(cosx ) (∗)

Так как $− 1 ≤ cosx ≤ 1$ , то $− tg1 ≤ tg(cosx ) ≤ tg1$ . Следовательно, значения правой части уравнения (*) принадлежат отрезку $2 2 [− tg 1;tg 1]$ .

Так как $x2 ≥ 0$ , то левая часть уравнения (*) больше или равна $0 + tg21$ .

Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны $2 tg 1$ . А это значит, что

{ 2 2 2 { 2x + tg 1 = tg 1 ⇔ x = 0 ⇔ x = 0 tg1 ⋅ tg(cosx ) = tg21 tg(cosx ) = tg1

Следовательно, значение $a = − tg1$ нам подходит.

Ответ:

$a ∈ {− tg1;0}$

Ошибка.
Попробуйте повторить позже

Задача 5#1086

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 2 x − |x+ a+ 3|= |x − a− 3|− (a+ 3)

имеет единственное решение.

Показать ответ и решение

Перенесем все слагаемые в левую часть:

2 2 x − |x + a+ 3|− |x− a− 3|+(a+ 3) = 0

Рассмотрим функцию: $f(x)= x2− |x+ a+ 3|− |x − a − 3|+ (a+ 3)2$ . Данная функция определена при всех $x∈ ℝ$ и является четной, так как $f(x)= f(−x)$ . Следовательно, для каждого $x0 >0$ , удовлетворяющего уравнению, существует также корень $− x0$ , удовлетворяющий уравнению. Следовательно, для того, чтобы уравнение имело единственный корень, его корнем должен быть только $x= 0$ .
Подставим $x= 0$ :

2 2 −|a +3|− |− a− 3|+ (a+ 3) = 0 ⇒ (a+ 3)− 2|a+ 3|= 0

Сделав замену $t =|a+ 3|$ , сведем уравнение к виду $t2− 2t= 0$ ; корнями будут $t=0$ и $t= 2$ . Следовательно,

[ ⌊a = −3 |a+ 3|= 0 | |a+ 3|= 2 ⇔ ⌈a = −1 a = −5

Проверим, действительно ли при этих значениях $a$ уравнение имеет только корень $x =0$ .
1) Подставим $a= −3$ :

x2− |x|− |x|=0 ⇔ x2− 2|x|= 0

Данное уравнение имеет корни: $x = 0;2;−2$ . Следовательно, $a = −3$ не подходит.
2) Подставим $a= −1$ :

2 2 x − |x +2|− |x − 2|+ 4 =0 ⇔ x +4 = |x +2|+ |x − 2|

Решим данное уравнение графически:

$PIC$

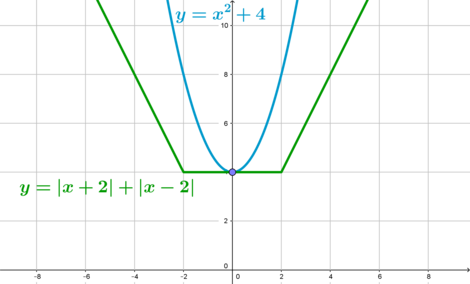
Убеждаемся, что уравнение действительно имеет ровно один корень.
3) Подставив $a= −5$ , получаем то же уравнение, что и при $a = −1$ .

Таким образом, окончательный ответ:

a∈ {−5;−1}

Ответ:

$a ∈{− 5;− 1}$

Ошибка.
Попробуйте повторить позже

Задача 6#31652

Найдите все значения параметра $a$ , при каждом из которых уравнение

x2+6ax+9a2 2 2 3 2 3 = ax +6a x+ 9a +a − 4a+4

имеет ровно одно решение.

Показать ответ и решение

Уравнение равносильно

(x+3a)2 2 2 3 − a(x +3a) =(a− 2)

Сделаем замену $t= x+ 3a$ . Так как замена линейная, то уравнение с заменой также должно иметь одно решение:

t2 2 2 3 − at = (a− 2)

Функция $f(t)= 3t2 − at2$ является четной, определенной при всех $t∈ ℝ$ , и уравнение имеет вид $f(t)= const$ . Следовательно, если это уравнение имеет решение $t0 ≥0$ , то оно имеет также решение $− t0 ≤ 0$ . Значит, количество решений уравнения будет четным, если среди решений нет $t= 0$ , и нечетным, если среди решений уравнения есть $t= 0$ . Так как нам требуется, чтобы уравнение имело единственное решение, что является нечетным количеством, то $t= 0$ — решение уравнения.

1.

Найдем, при каких $a$ число $t= 0$ является решением уравнения:

30− a ⋅0 =(a− 2)2 ⇔ a= 1;3

2.

Проверим, является ли $t= 0$ единственным корнем уравнения при найденных $a$ или уравнение имеет другие корни. Для этого заметим, что если мы определим хотя бы один корень $t1 ⁄= 0$ , то найденные значения параметра нам не подойдут; если же мы докажем, что других корней нет, то найденные $a$ нам подходят.

При $a= 1$ уравнение имеет вид

t2 2 3 − t = 1

Сделаем замену $t2 = p$ и рассмотрим функцию $y(p)= 3p− p$ на промежутке $p ∈[0;+∞ )$ . Тогда уравнение примет вид $y(p)=1$ . Найдем ее производную $′ p y(p)=3 ln3− 1$ . Найдем нули производной:

3p = log3e ⇔ p= log3log3e

Так как $e< 3$ , то $log3e< 1$ , следовательно, $log3log3e< 0$ . Следовательно, при $p ≥0$ производная принимает значения одного знака, значит, функция $y(p)$ строго монотонна при $p≥ 0$ . Тогда уравнение вида $y(p)=const$ имеет не более одного решения. И это решение мы знаем — это $p =t2 = 0$ . Следовательно, других решений нет.

Значит, $a =1$ нам подходит.

При $a= 3$ уравнение имеет вид

3t2 − 3t2 =1

Сделаем замену $t2 = p$ и рассмотрим функцию $g(p)= 3p − 3p$ на промежутке $p∈[0;+ ∞)$ . Тогда уравнение примет вид $g(p)=1$ . Заметим, что при $p= 1$ имеем $g(1)= 0< 1$ , а при $p=2$ имеем $g(2)= 3> 1$ . Следовательно, существует точка $p1 ∈ (1;2)$ , в которой $g(p1)= 1$ и эта точка отлична от $p= t2 = 0$ . Таким образом, уравнение имеет как минимум еще один корень $t1 =√p1-∈(1;√2)$ помимо $t= 0$ .