Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых наибольшее значение функции
не меньше .
Наибольшее значение функции не меньше , если неравенство
имеет хотя бы одно решение. Так как модульное неравенство
решается следующим образом:
то получаем, что должно иметь хотя бы одно решение следующее неравенство
Совокупность из двух неравенств имеет решения, когда хотя бы одно из неравенств имеет решение. У нас два квадратичных неравенства
с положительным старшим коэффициентом. Неравенство вида имеет решения, когда парабола
(ветви
которой направлены вверх) имеет хотя бы одну точку пересечения с осью абсцисс. Следовательно, дискриминант этого квадратичного
трехчлена должен быть неотрицательным. Таким образом, для совокупности из двух квадратичных неравенств такого вида получаем, что
решения будут, если
Отсюда ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых множество значений функции
Перепишем функцию в виде
Сделаем замену , тогда новая функция
1 способ
Так как функция непрерывна на всей области определения, то область значений функции содержит отрезок
, если существуют такие точки
и
, что
и
. Следовательно, следующие
уравнения должны иметь хотя бы по одному неотрицательному решению (т.к. функция определена для всех
неотрицательных чисел):
При уравнение 1 не имеет решений, при
уравнение 2 не имеет решений. Следовательно, эти значения
параметра нам не подходят. При остальных
уравнения 1 и 2 можно переписать в виде:
2 способ
Графиком функции является часть ветви гиперболы при
и константа при
. Заметим, что при
функция
возрастает, а при
убывает. Имеем:
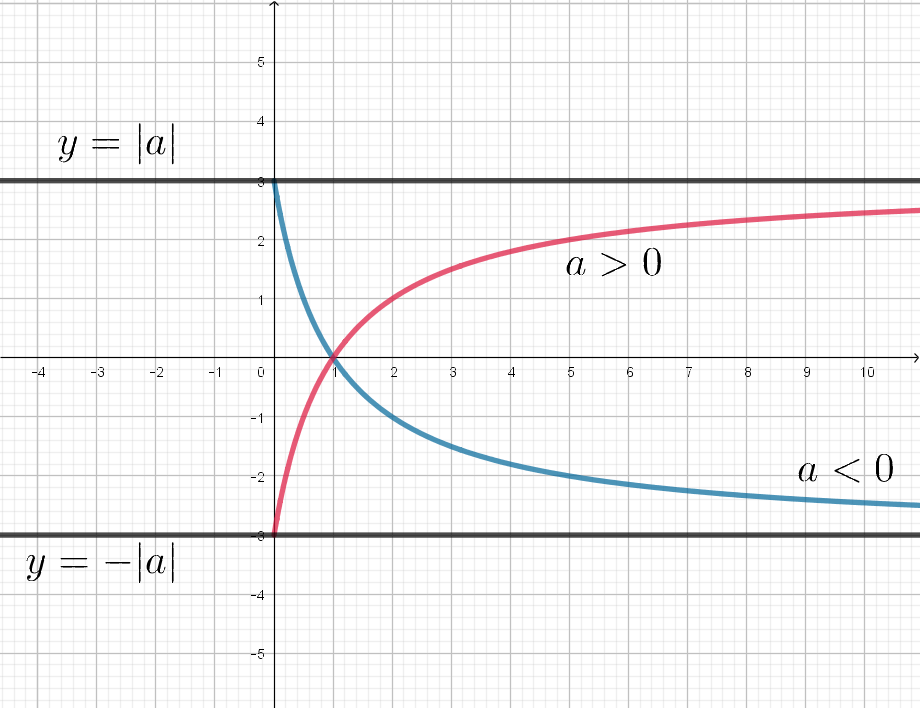
Таким образом, чтобы область значений функции содержала отрезок
, нужно, чтобы
Случай мы не рассматриваем, так как функция, являющаяся константой, графически представляет собой
горизонтальную прямую, следовательно, принимает только одно значение, то есть область ее значений не может
содержать отрезок.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых среди значений функции
есть ровно одно целое число.
Исследуем функцию через ее производную:
Дискриминант числителя равен
Следовательно, производная при любом имеет два нуля, причем заметим, что они разных знаков, так как их произведение равно
. Назовем их
и
. Найдем знаки производной на промежутках, образованных этими нулями:
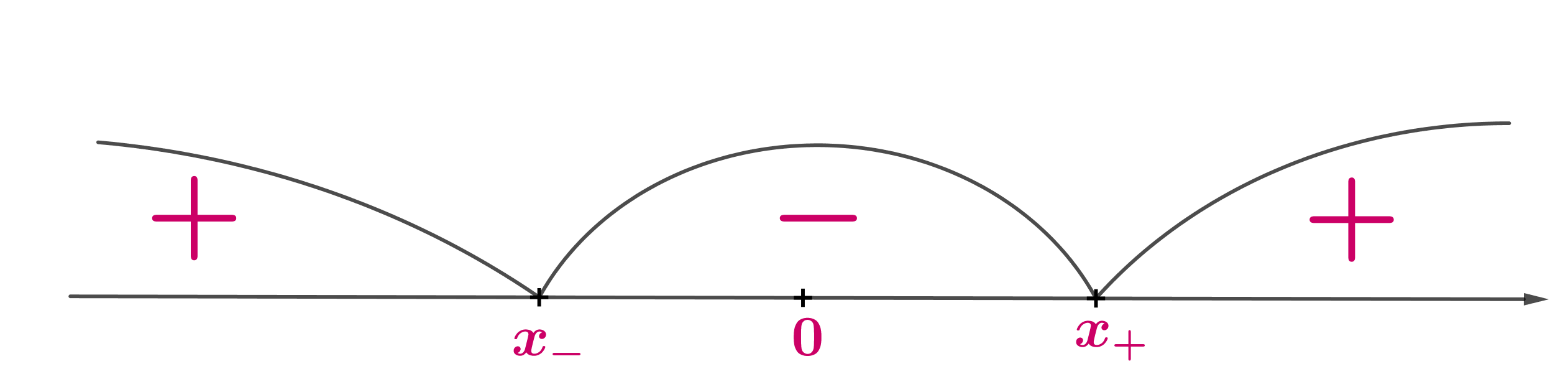
Заметим, что при имеем
, следовательно, схематично график функции
выглядит так:
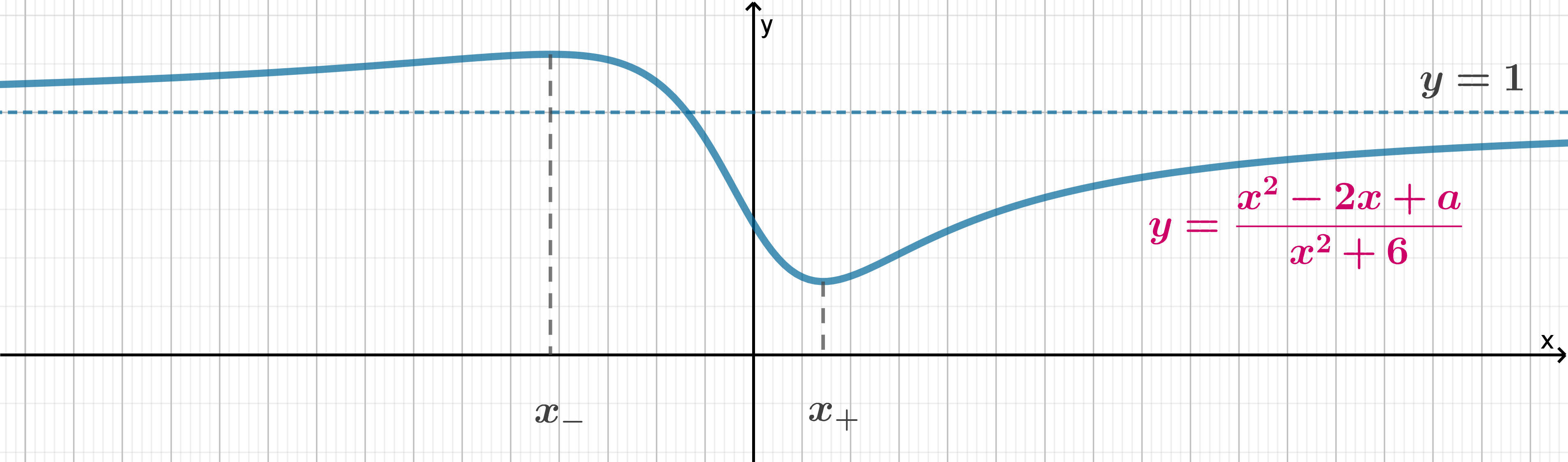
Таким образом, облласть значений функции и она точно содержит число
. Следовательно, чтобы других целых
чисел не было в области значений функции, нужно, чтобы
и
. Эти требования можно задать альтернативным
условием: следующее неравенство должно быть выполнено для всех
Чтобы полученная система имела решения , каждое из неравенств должно иметь такие решения, следовательно, дискриминанты
квадратичных трехчленов должны быть отрицательны одновременно:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых множество значений функции
содержит отрезок .
Заметим, что знаменатель для любого
. Следовательно, у функции нет точек разрыва и ее область определения
, то есть функция непрерывна на всем
. Значит условие задачи будет выполняться, если каждое из двух неравенств
и
будет иметь хотя бы одно решение. Рассмотрим каждое из двух неравенств.
1)
Это неравенство будет иметь решения тогда и только тогда, когда дискриминант левой части будет неотрицательным:
2)
Если , то данное линейное неравенство имеет решения. Если
, то неравенство не имеет решений.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых область значений функции
содержится в интервале .
Заметим, что при
. следовательно, область значений функции будет содержаться в интервале
, если каждое из
равенств
и
не имеет решений, то есть не имеет решений совокупность из них:
Данная совокупность не имеет решений, когда каждое из уравнений не имеет решений, следовательно, их дискриминанты одновременно меньше нуля:
Получаем
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых область значений функции
содержит отрезок .
Сделаем замену ,
,
,
. Тогда функция выглядит как
Заметим, что знаменатель дроби , следовательно, не равен нулю, следовательно, функция непрерывна на всей
области определения. Исследуем эту функцию через производную:
Так как ,
, то производная
Следовательно, функция
убывает при всех
. Значит, ее максимальное значение достигается при
, а минимальное — при
. Следовательно, область значений
функции будет содержать отрезок
, если
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение параметра , при котором система
имеет хотя бы одно решение. Найдите решения системы при данном .
Рассмотрим второе уравнение системы. Сделаем замену ,
, тогда уравнение примет вид
Это уравнение при должно иметь хотя бы одно решение
, причем эти значения
и
должны удовлетворять первому
уравнению. Дискриминант уравнения
:
Рассмотрим :
Следовательно, имеет два нуля, причем, так как
, то условию
удовлетворяет только один корень, назовем его
. Тогда при
имеем
, при
имеем
, значит, рассматриваем только
Тогда
имеет
один или два корня.
Обратим внимание, что абсцисса вершины параболы (так как
),
, следовательно,
чтобы хотя бы один корень удовлетворял условию
, парабола
должна выглядеть следующим образом:
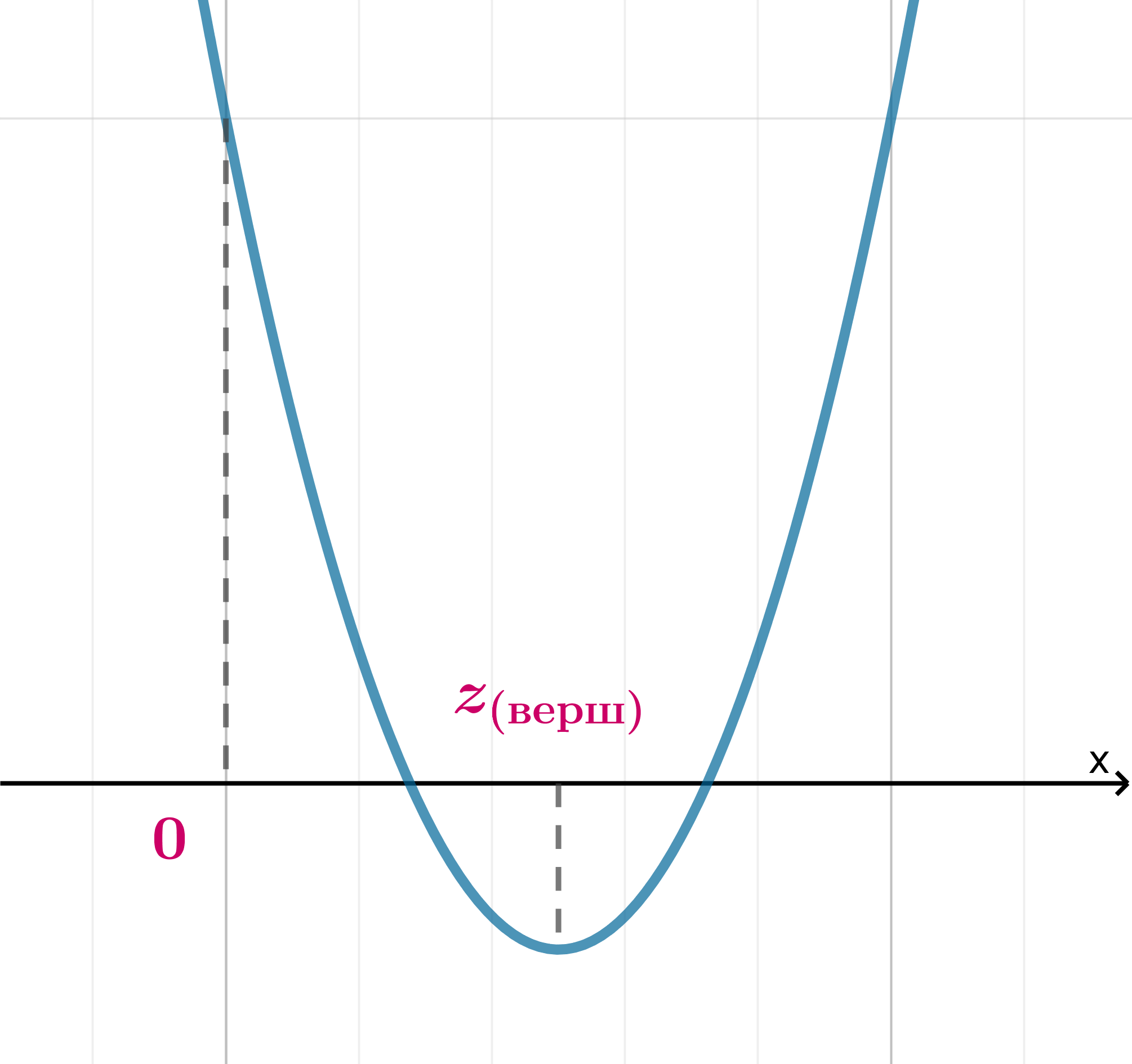
Поэтому только левый корень может удовлеторять условию и для этого нужно, чтобы
, откуда
.
Так как , то при
уравнение
имеет корень
.
Рассмотрим первое уравнение системы:
Следовательно, наименьшее . Тогда при нем должно быть выполнено
,



