Ошибка.
Попробуйте повторить позже
Середина одной из боковых сторон трапеции равноудалена от двух не принадлежащих этой стороне вершин. Докажите, что трапеция прямоугольная.
Пусть в трапеции точки
и
— середины сторон
и
соотвественно. Тогда по условию
и
— равнобедренный.
Следовательно, медиана является также и высотой, то есть
. Но по определению
— средняя линия
трапеции, следовательно, параллельна основаниям. Тогда имеем:
Ошибка.
Попробуйте повторить позже
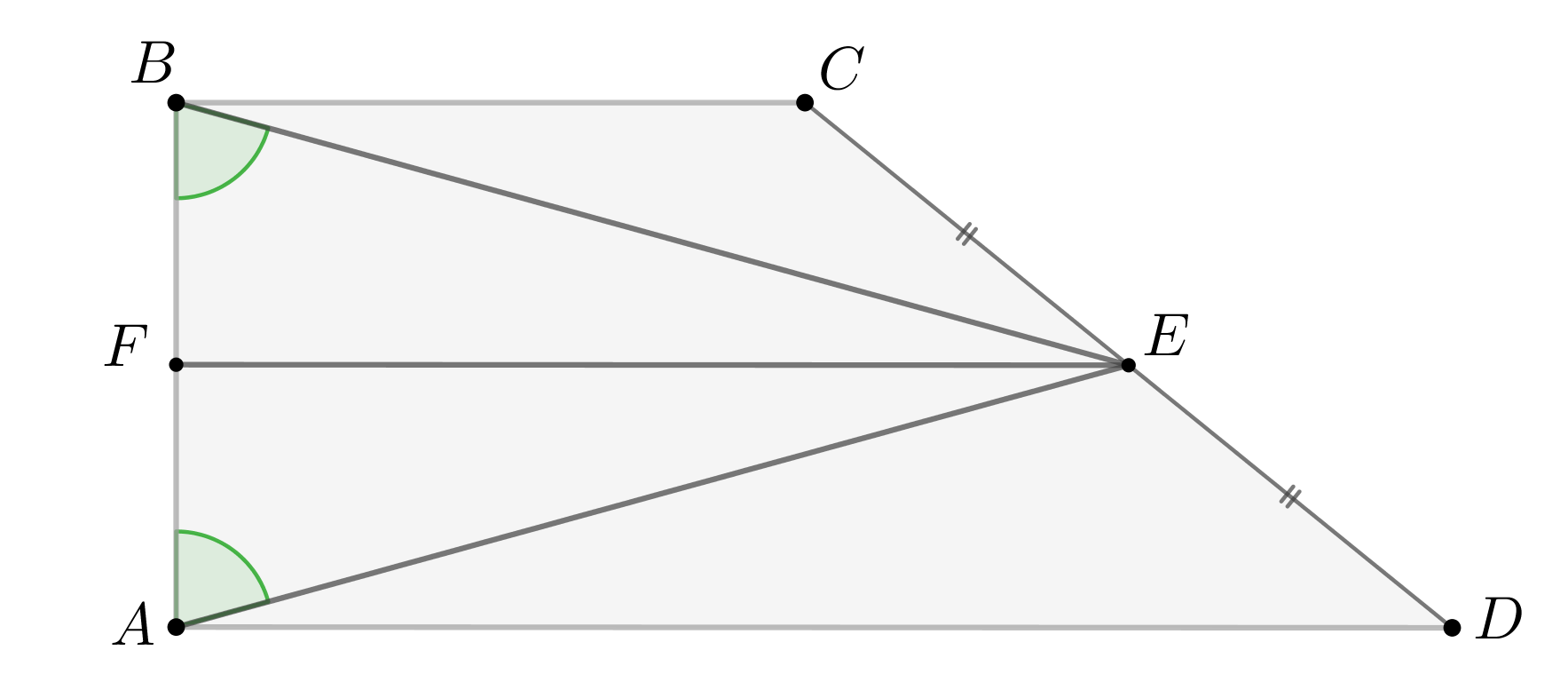
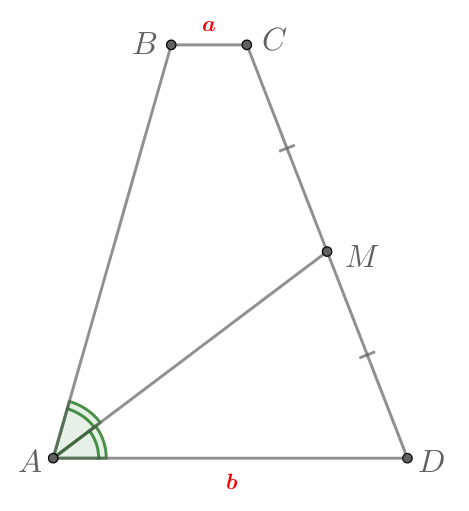
Биссектриса одного из углов трапеции делит ее боковую сторону пополам. Найдите другую боковую сторону трапеции, если
основания равны и
.
В трапеции с основаниями
и
продлим биссектрису
до пересечения с прямой
в точке
. Тогда
и
в силу вертикальности и параллельности
соответственно, значит
и
подобны. Коэффициент их подобия равен 1, так как по условию
и эти стороны лежат в треугольниках
напротив равных углов. Тогда
.
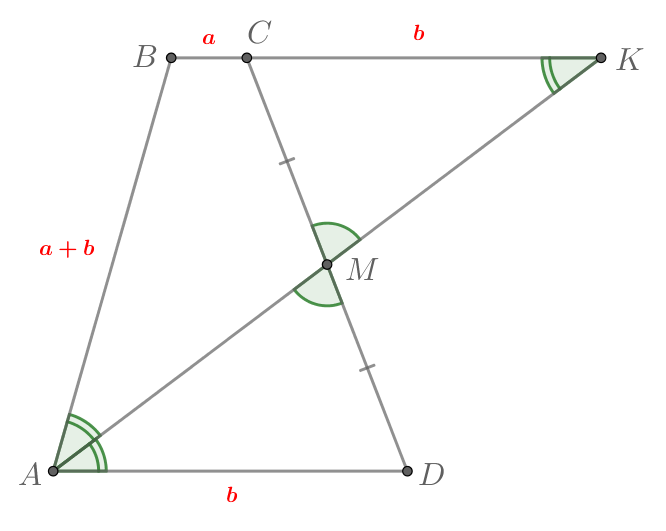
Рассмотрим треугольник . Его угол
равен углу
, так как
— биссектриса угла
. С другой
стороны,
как накрест лежащие при
и секущей
. Тогда
и в равнобедренном
имеем:
Ошибка.
Попробуйте повторить позже
Основания трапеции равны и
где
Найдите длину отрезка, соединяющего середины диагоналей
трапеции.
Нам известно, что средняя линия трапеции проходит через середины диагоналей. Тогда как средние линии в
треугольниках
и
соответственно. Тогда искомый отрезок
Ошибка.
Попробуйте повторить позже
Диагональ равнобедренной трапеции равна 10 и образует угол с основаниями трапеции. Найдите среднюю линию
трапеции.
Пусть — точка пересечения диагоналей. В равнобокой трапеции
, причем все
эти углы равны
, следовательно, треугольники
и
— равносторонние. Обозначим
,
.
Тогда диагональ
. Получаем, что средняя линия трапеции равна
.
![]()
5
Ошибка.
Попробуйте повторить позже
Произвольную точку внутри равностороннего треугольника
соединили с его вершинами. Докажите, что на каждой
стороне треугольника можно выбрать по одной точке так, чтобы расстояния между этими точками были равны
,
и
.
Проведем через точку прямые
параллельные сторонам
соответственно.
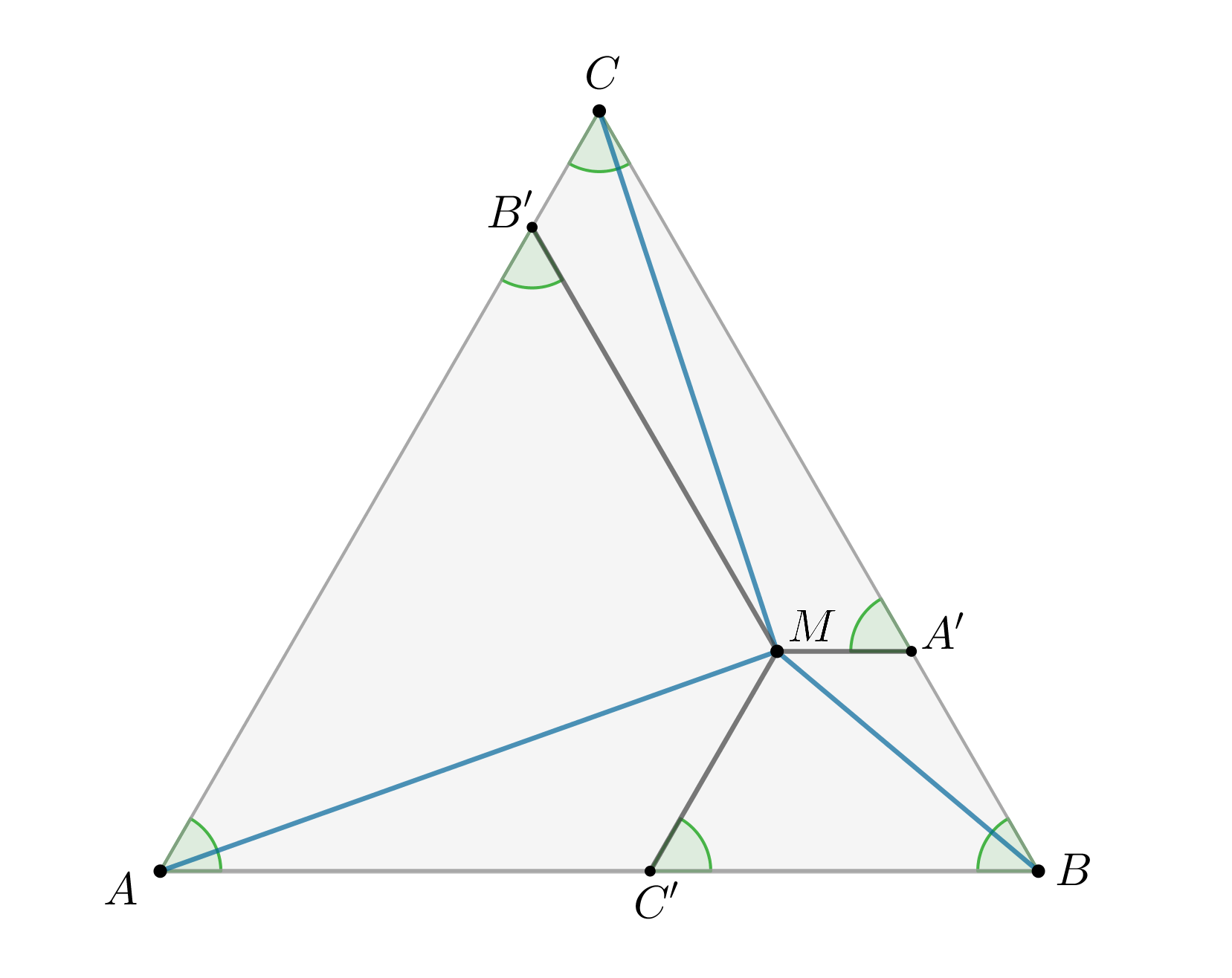
Тогда как соответственные равны углы Следовательно,
разбился на
три равнобедренные трапеции
Диагонали равнобедренной трапеции равны, следовательно, Тогда треугольник
образован тремя искомыми точками.
Ошибка.
Попробуйте повторить позже
Основания равнобедренной трапеции равны и
(
), острый угол равен
Найдите площадь
трапеции.
Опустим высоты и
на большее основание
.
![]()
Трапеция равнобокая, ,
, следовательно, прямоугольные треугольники
и
равны и
.
— прямоугольник, значит,
. Тогда
|
AE = FD = |
Прямоугольный треугольник с углом 45
является равнобедренным и
. Тогда площадь
трапеции
|
SABCD = |
Ошибка.
Попробуйте повторить позже
Основания трапеции равны 1 и 6, а диагонали — 3 и 5. Под каким углом видны основания из точки пересечения диагоналей?
Пусть — точка пересечения диагоналей. Треугольники
и
подобны с коэффициентом
, тогда
По теореме косинусов для треугольника
Угол меньше
, его косинус равен
, следовательно, угол равен
.
![]()
Ошибка.
Попробуйте повторить позже
В равнобедренной трапеции основания равны 40 и 24, а ее диагонали взаимно перпендикулярны. Найдите площадь трапеции.
![]()
Пусть — точка пересечения диагоналей. В равнобокой трапеции
,
следовательно, треугольники
и
— прямоугольные равнобедренные. Тогда
,
. Площадь выпуклого четырехугольника с перпендикулярными диагоналями равна
полупроизведению диагоналей, то есть
|
SABCD = |
1024
Ошибка.
Попробуйте повторить позже
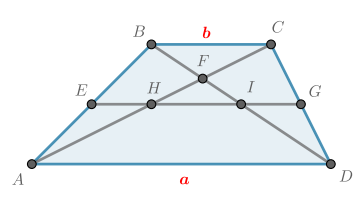
Основания трапеции равны
и
Найдите:
а) длину средней линии, параллельной основаниям;
б) длину отрезка, соединяющего середины диагоналей.
-
а)
-
Пусть
— средняя линия трапеции
, то есть отрезок, соединяющий середины боковых сторон. Пусть также
,
. Проведем
,
. Тогда по определению
— параллелограмм, следовательно,
. Тогда
. По теореме Фалеса из
и
следует, что
, следовательно,
— средняя линия в
. Значит,
.
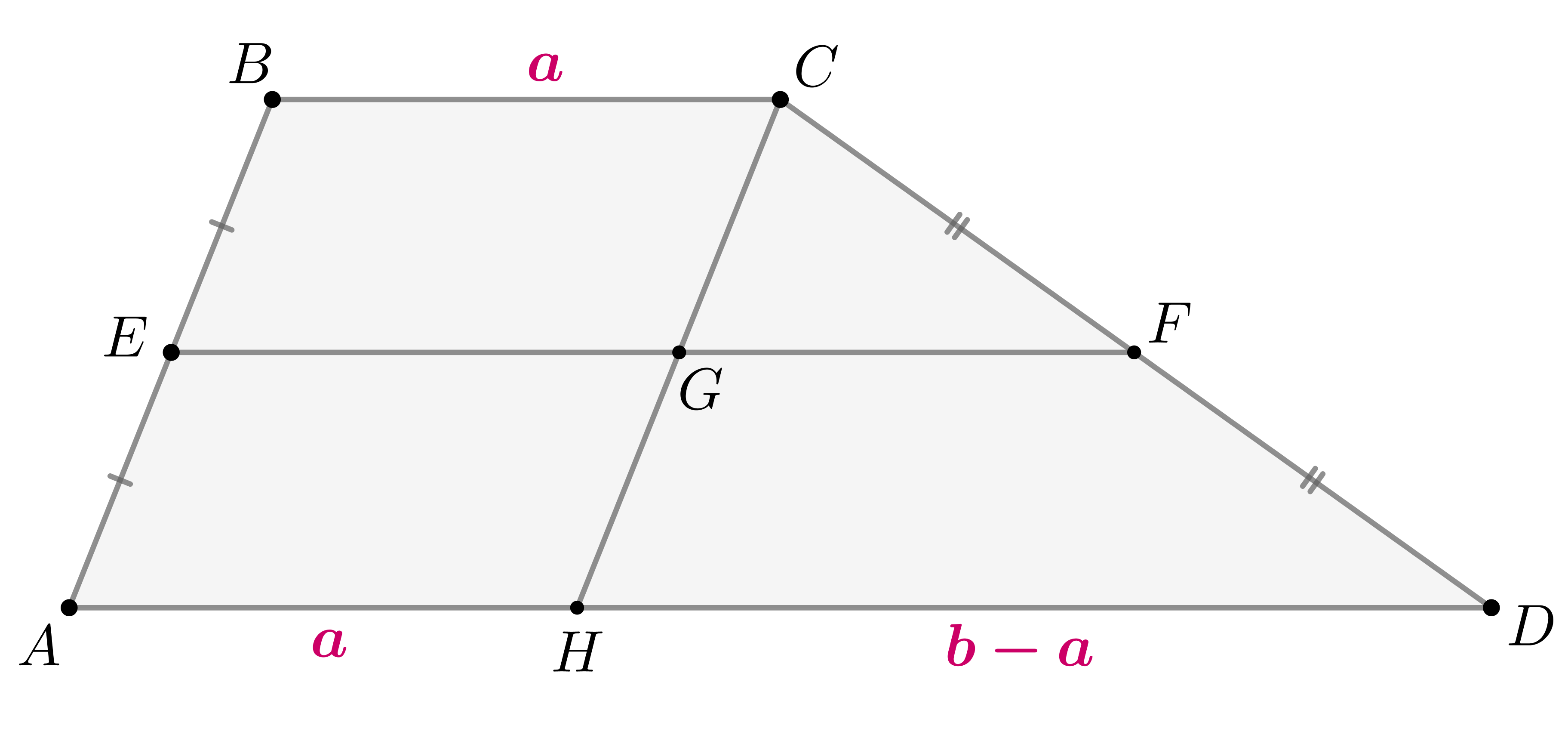
Четырехугольник
также является параллелограммом, следовательно,
.
Тогда
-
б)
-
Пусть
пересекает диагонали трапеции в точках
и
. Тогда из теоремы Фалеса следует, что
и
— середины диагоналей. Следовательно, требуется найти отрезок
.
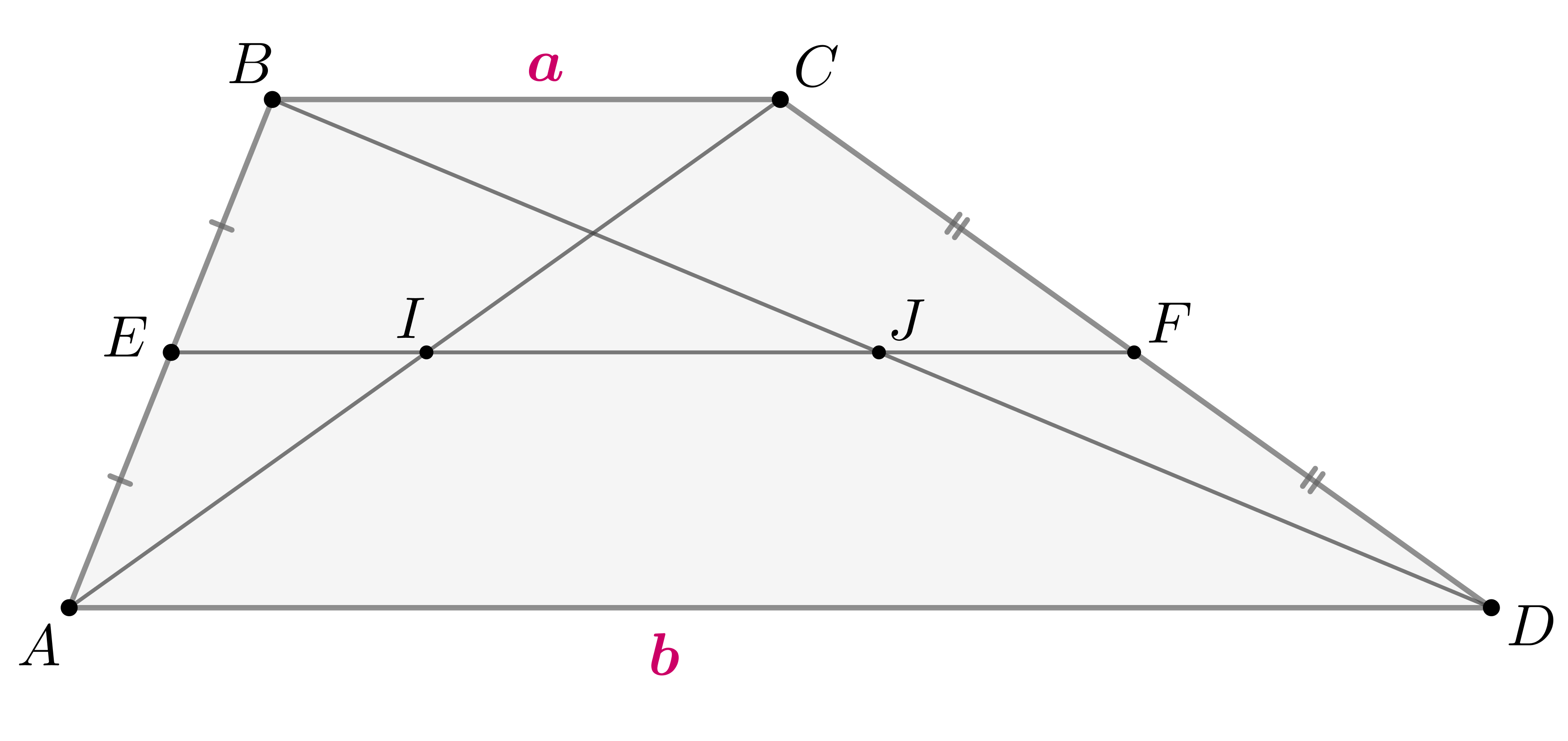
Заметим, что
и
— средние линии в
и
соответственно, параллельные общему основанию
. Следовательно,
. Тогда
P.S
Если
и
, то
. Следовательно, в общем случае ответ:
.
а)
б)
Ошибка.
Попробуйте повторить позже
Докажите, что точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований любой трапеции лежат на одной прямой.
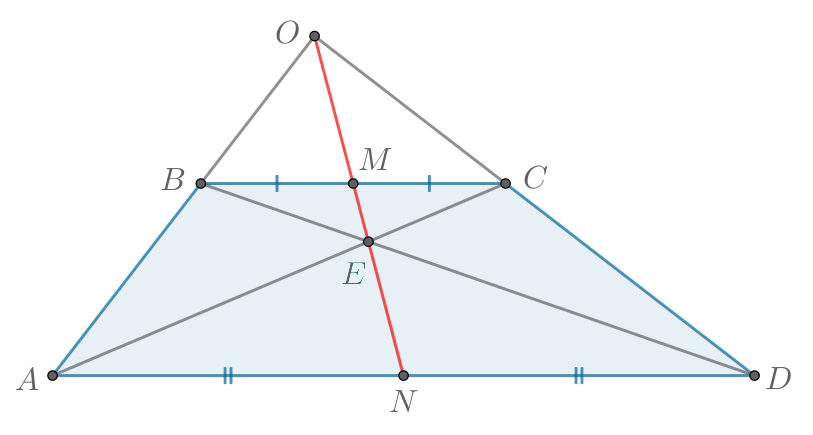
Пусть точки и
— середины оснований
и
трапеции соответственно,
— точка пересечения диагоналей,
— точка
пересечения прямых, содержащих боковые стороны трапеции.
Сначала докажем, что на одной прямой лежат точки ,
и
.
Пусть — точка пересечения
и
. Тогда
по двум углам
,
— общий) с
коэффициентом
.
Аналогично тоже с коэффициентом
.
Из первого подобия: .
Из второго подобия: .
При этом совпадает с серединой
основания
и точки
,
,
лежат на одной
прямой.
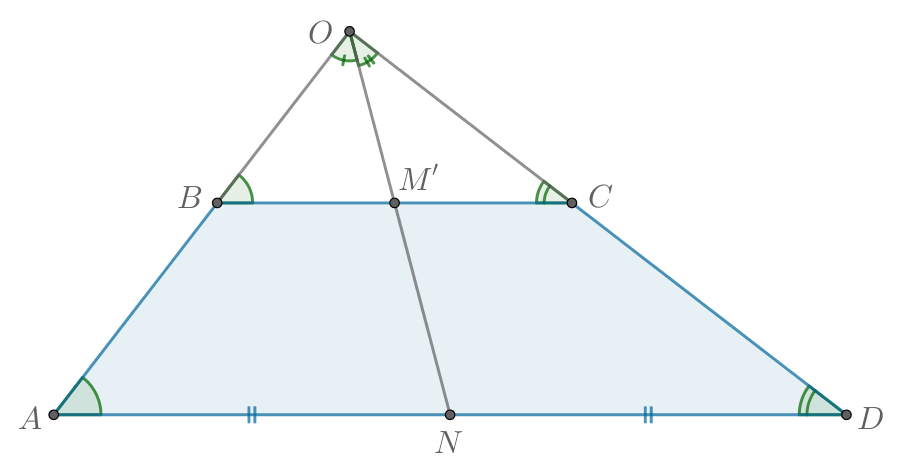
Теперь докажем, что на одной прямой лежат точки ,
и
(в совокупности с предыдущим фактом из этого следует, что все
четыре точки лежат на прямой
)
Пусть — точка пересечения
и
. Тогда
по двум углам
,
как
вертикальные) с коэффициентом
.
Аналогично тоже с коэффициентом
.
Из первого подобия: .
Из второго подобия: .
При этом совпадает с серединой
основания
и точки
,
,
лежат на одной
прямой.
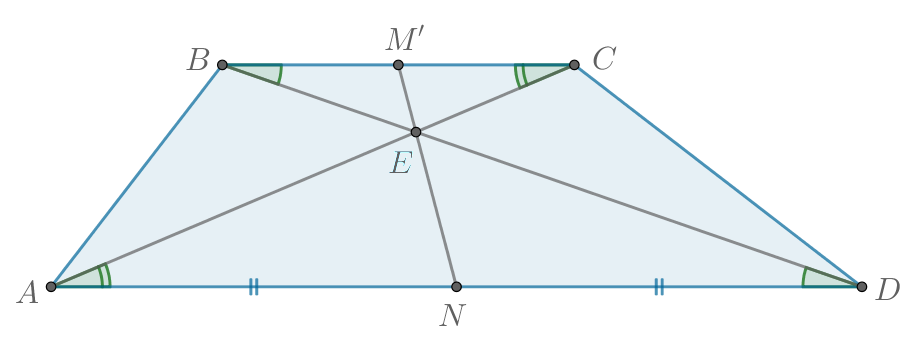
Тогда точки ,
,
,
лежат на одной прямой.
Ошибка.
Попробуйте повторить позже
Через точку пересечения диагоналей трапеции
с основаниями
и
проведена прямая, параллельная основаниям.
Найдите отрезок этой прямой, заключенный между боковыми сторонами трапеции.
Пусть прямая, проведенная через точку параллельно основаниям, пересекает боковые стороны трапеции
и
в точках
и
соответственно.
Рассмотрим треугольники и
. В них
и
как накрест лежащие. Значит,
по двум углам. Тогда
Аналогично
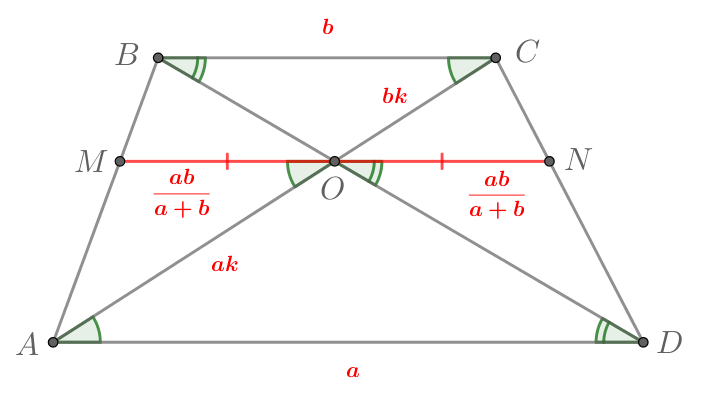
Рассмотрим треугольники и
. Они подобны, так как
по условию. Тогда
Рассмотрим треугольники и
. Они подобны, так как
по условию. Тогда
Таким образом,
Заметим, что сейчас мы доказали равенство отрезков и
. Таким образом, мы получили, что отрезок, параллельный
основаниям трапеции и проведенный через точку пересечения диагоналей, делится этой точкой пополам.
Ошибка.
Попробуйте повторить позже
Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
Пусть — центр окружности.
. Опустим перпендикуляры
и
на
и
соответственно.
, следовательно,
,
и
лежат на одной прямой и
— высота
трапеции.
Треугольники и
— равнобедренные, следовательно,
— середина
,
— середина
. Тогда
. Запишем теоремы Пифагора для треугольников
и
Далее возможны два случая (первая часть решения для них общая): центр окружности лежит внутри трапеции, либо снаружи трапеции.
- 1.
- Если центр лежит внутри, высота трапеции будет равна сумме отрезков
и
HG = HO + GO = 39 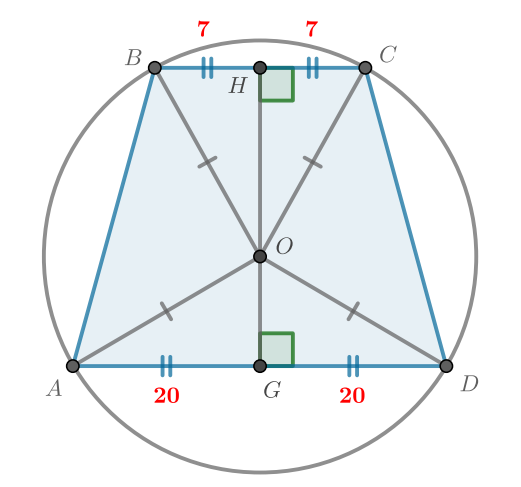
- 2.
- Если центр лежит вне трапеции, высота трапеции будет равна разности отрезков
и
HG = HO − GO = 9 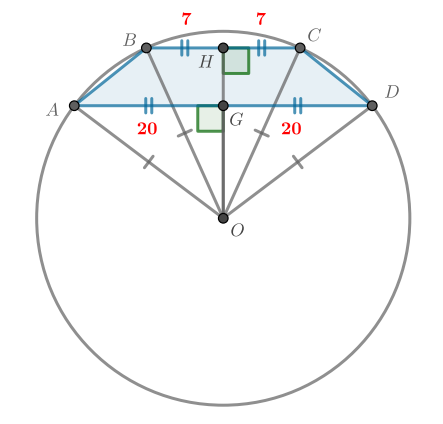
39 или 9
Ошибка.
Попробуйте повторить позже
Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5.
Пусть ,
, тогда из условия про длину средней линии имеем
. Пусть
— точка пересечения диагоналей. В равнобокой трапеции
, следовательно,
треугольники
и
— прямоугольные равнобедренные. Тогда
,
.
![]()
Площадь выпуклого четырехугольника с перпендикулярными диагоналями равна полупроизведению диагоналей, то есть
25
Ошибка.
Попробуйте повторить позже
На боковых сторонах и
трапеции
взяты точки
и
соответственно так, что отрезок
параллелен
основаниям и делит площадь трапеции пополам. Найдите длину
если
и
Пусть . Проведем
, тогда
и
. Пусть
.
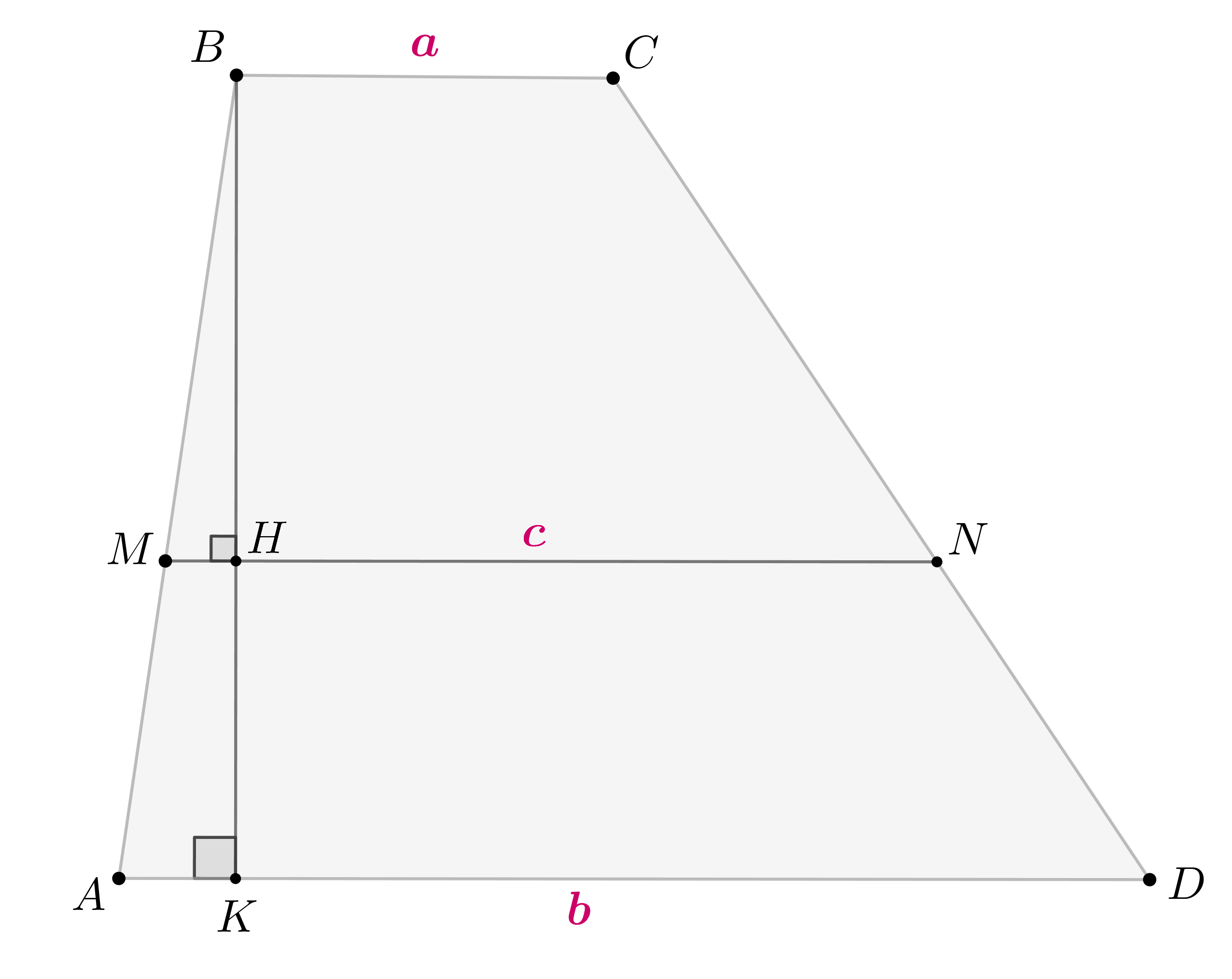
Тогда
Тогда получаем:
Ч.т.д.
Ошибка.
Попробуйте повторить позже
Непараллельные стороны трапеции продолжены до взаимного пересечения и через полученную точку проведена прямая, параллельная
основаниям трапеции. Найдите длину отрезка между точками пересечения этой прямой с продолжениями диагоналей, если длины оснований
трапеции равны и
.
Пусть боковые стороны и
трапеции
пересекаются в точке
, через которую проведена параллельная основаниям
прямая, пересекающая продолжения диагоналей
и
в точках
и
соответственно. Пусть
,
и
.
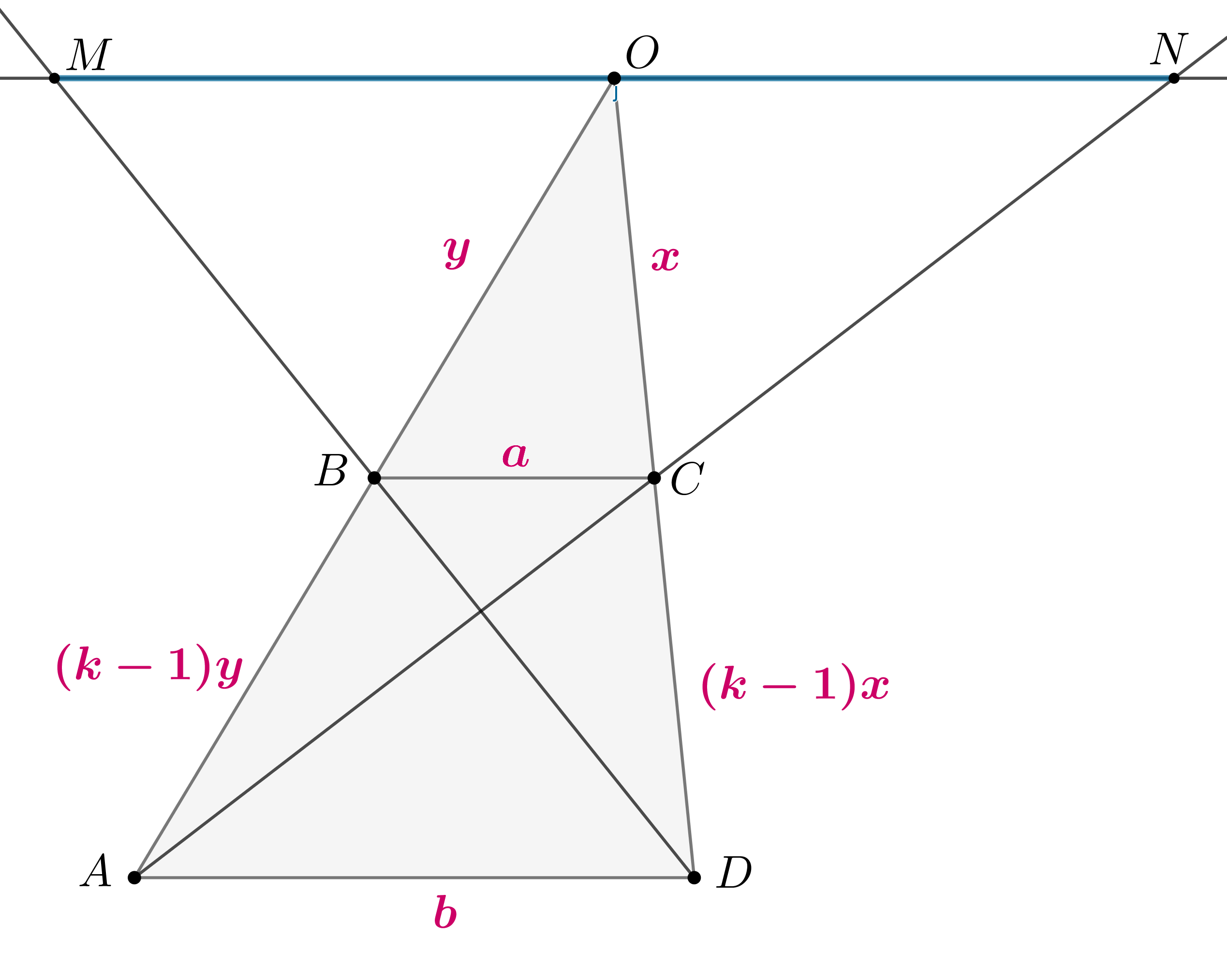
Тогда по двум углам (
,
как соответственные при
и секущих
и
соответственно). Пусть коэффициент подобия треугольников
и
равен
. Тогда, если
, то
,
следовательно,
.
Из подобия по двум углам (
как вертикальные и
как накрест лежащие при
и секущей
) имеем:
Аналогично из подобия с коэффициентом подобия
имеем:
Следовательно, искомая длина равна
P.S. Если , то получим
, следовательно, объединяя оба случая, получаем ответ
.
Ошибка.
Попробуйте повторить позже
Заключенный внутри трапеции отрезок прямой, параллельной основаниям трапеции, разбивается ее диагоналями на три части. Докажите, что части, прилегающие к боковым сторонам трапеции, равны между собой.
Пусть — параллельный основаниям трапеции
отрезок, который пересекает бооковые стороны в точках
,
, а диагонали
в точках
,
.
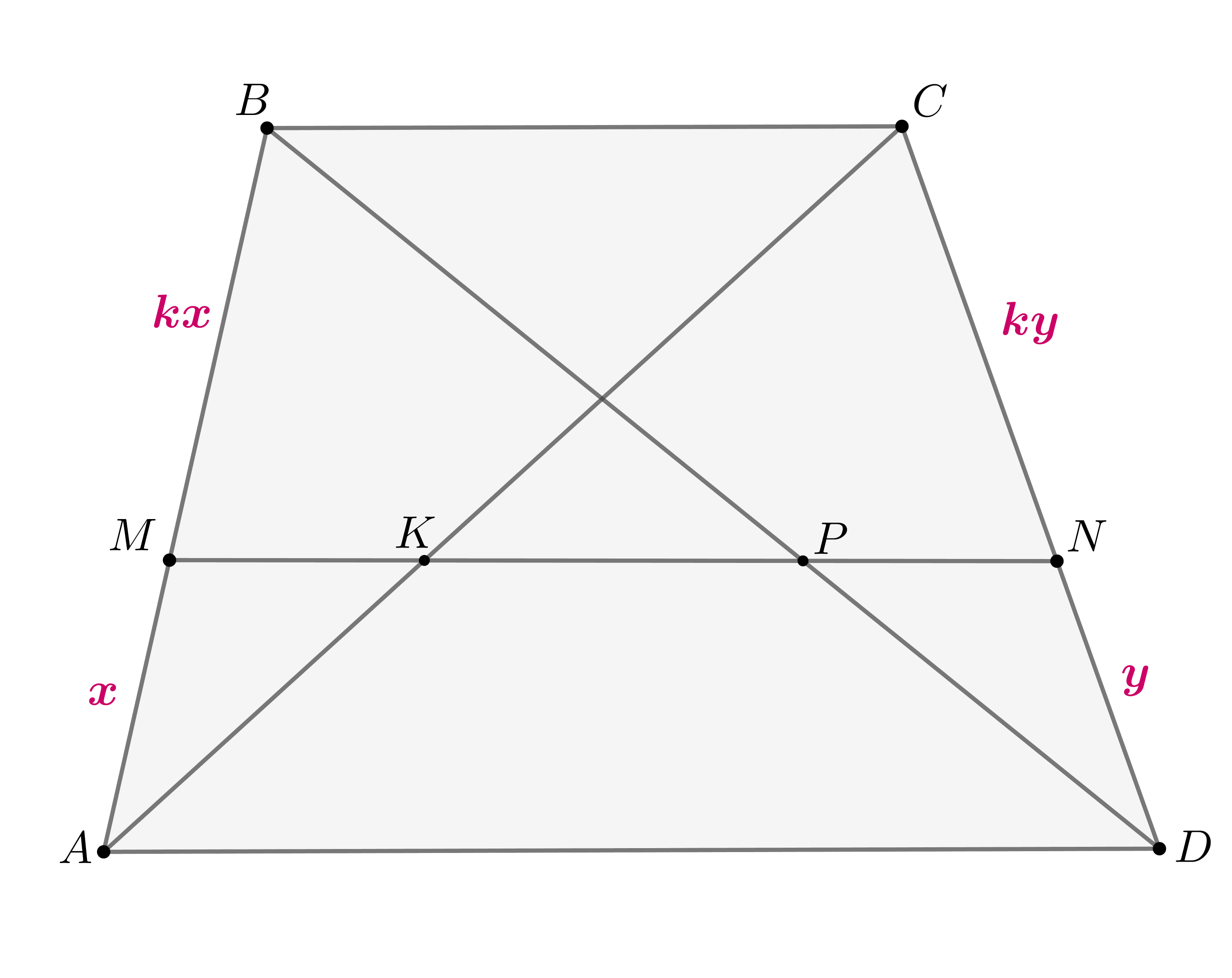
Тогда по теореме Фалеса . Пусть
,
,
,
.
Из подобия (
— общий,
как соответственные при
и секущей
)
имеем:
Аналогично из подобия имеем:
Следовательно,
Ч.т.д.



