Ошибка.
Попробуйте повторить позже
В треугольнике медиана
в два раза меньше стороны
и образует с ней угол
. Найдите угол
. Ответ дайте в
градусах.
Пусть — точка, симметричная точке
относительно
. Тогда
и
— параллелограм (так как диагонали делят
друг друга пополам).
, следовательно, треугольник
— равнобедренный с углом
между равными
сторонами. Тогда по сумме углов треугольника
Кроме того, , следовательно,
, тогда
.
![]()
Ошибка.
Попробуйте повторить позже
На медиане треугольника
взяли точку
так, что угол
равен углу
. Докажите, что отрезок
равен одной из
сторон треугольника.
![]()
Продлим медиану за точку
на свою длину. Назовём полученную точку —
.
![]()
Рассмотрим треугольники и
. Они равны, так как
по построению,
по условию и
как вертикальные. В равных треугольниках соответственные элементы равны, в частности,
и
.
По условию , значит,
, следовательно, треугольник
— равнобедренный, то есть
.
Тогда
, значит, отрезок
равен стороне
треугольника
.
Ошибка.
Попробуйте повторить позже
Медиана треугольника совпадает с его биссектрисой. Верно ли, что он равнобедренный?
Пусть медиана треугольника
также является биссектрисой угла
. Тогда продлим медиану
за точку
на свою
длину. Назовём полученную точку
.
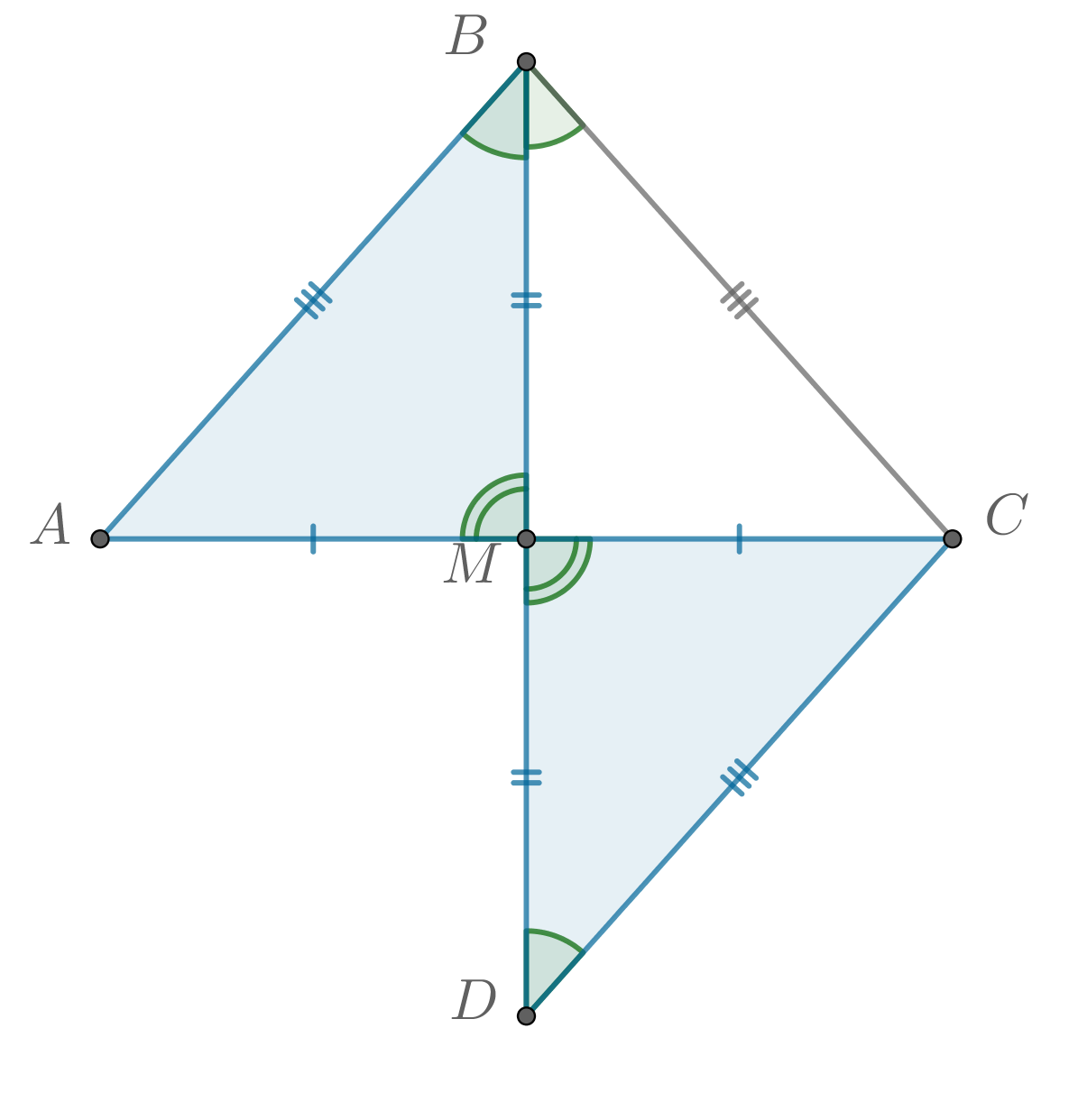
Рассмотрим треугольники и
. Они равны, так как
по построению,
по условию и
как вертикальные. В равных треугольниках соответственные элементы равны, в частности,
и
.
Так как — биссектриса угла
, имеем:
Таким образом, треугольник — равнобедренный, то есть
, значит,
.
Ошибка.
Попробуйте повторить позже
В треугольнике точка
— середина стороны
На стороне
взяли точку
так, что угол
прямой. Оказалось, что
Найдите
если
Ответ дайте в градусах.
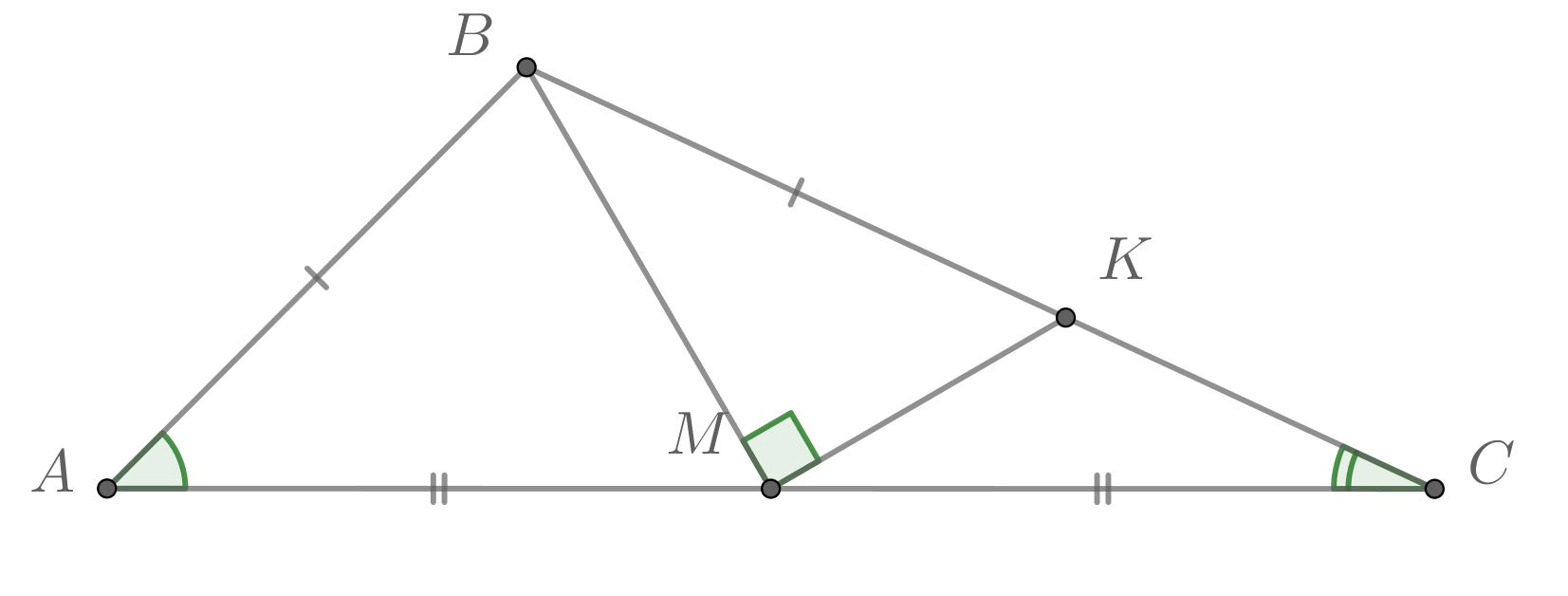
Продлим медиану за точку
на свою длину. Назовём полученную точку
Рассмотрим треугольники и
Они равны, так как
по построению,
по условию и
как вертикальные. В равных треугольниках соответственные элементы равны, в частности,
и
![]()
Рассмотрим треугольник В нем высота
является также медианой, так как
, следовательно,
Тогда
значит, треугольник
равнобедренный, и
Углы и
— смежные, значит,
В равнобедренном треугольнике высота
также является и биссектриссой угла
следовательно,
Ошибка.
Попробуйте повторить позже
Докажите, что два треугольника равны по двум сторонам и медиане, проведенной к третьей стороне.
Пусть в и
имеется
,
,
— медианы. Докажем, что треугольники равны.
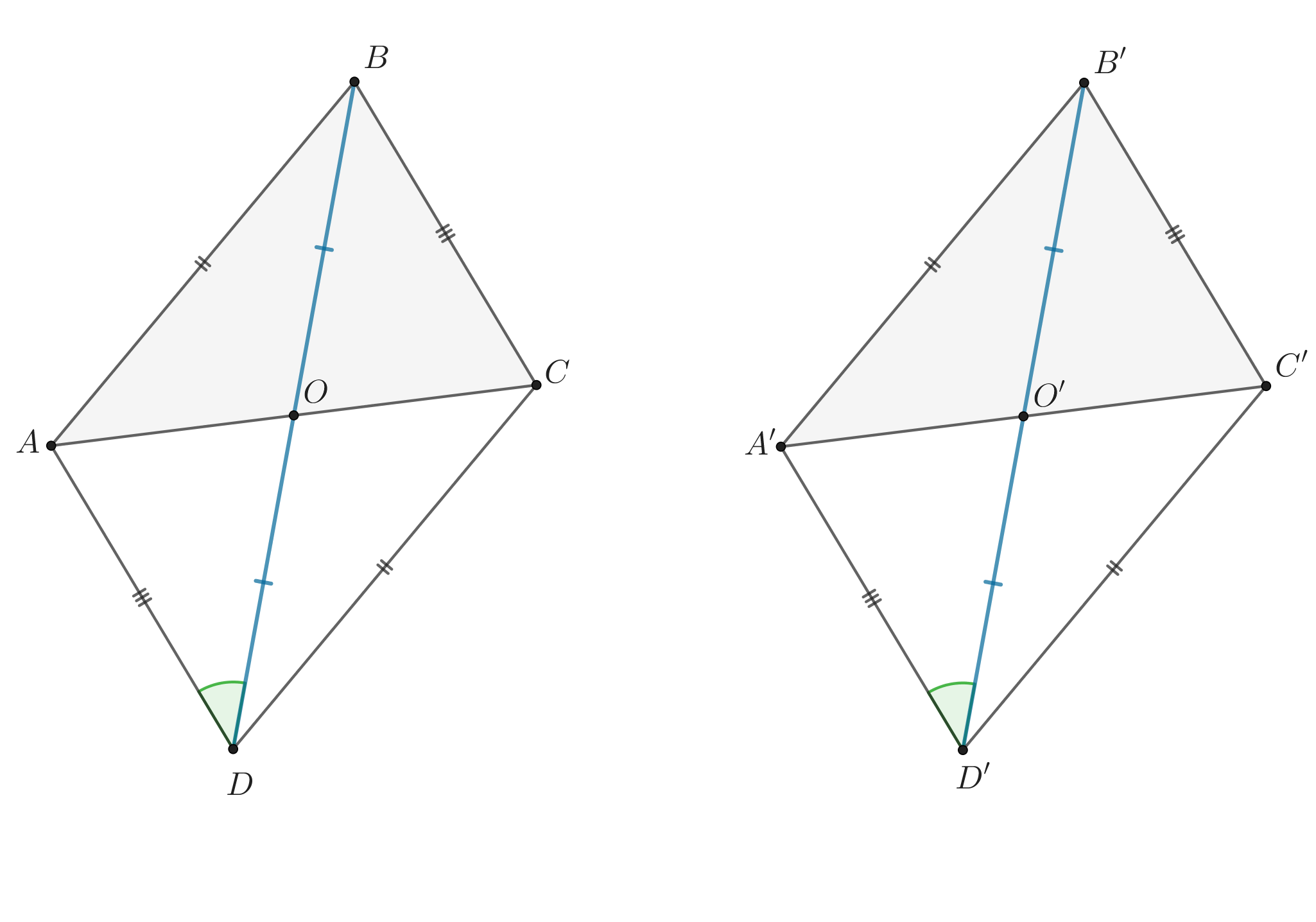
Продлим медианы и
за точки
и
так, чтобы
,
. Получим два параллелограмма
и
. Рассмотрим
и
. Они равны по трем сторонам, следовательно,
. Тогда, в свою очередь,
по углам
и
,
. Следовательно,
. Но тогда
. Следовательно,
по трем сторонам. Ч.т.д.
Ошибка.
Попробуйте повторить позже
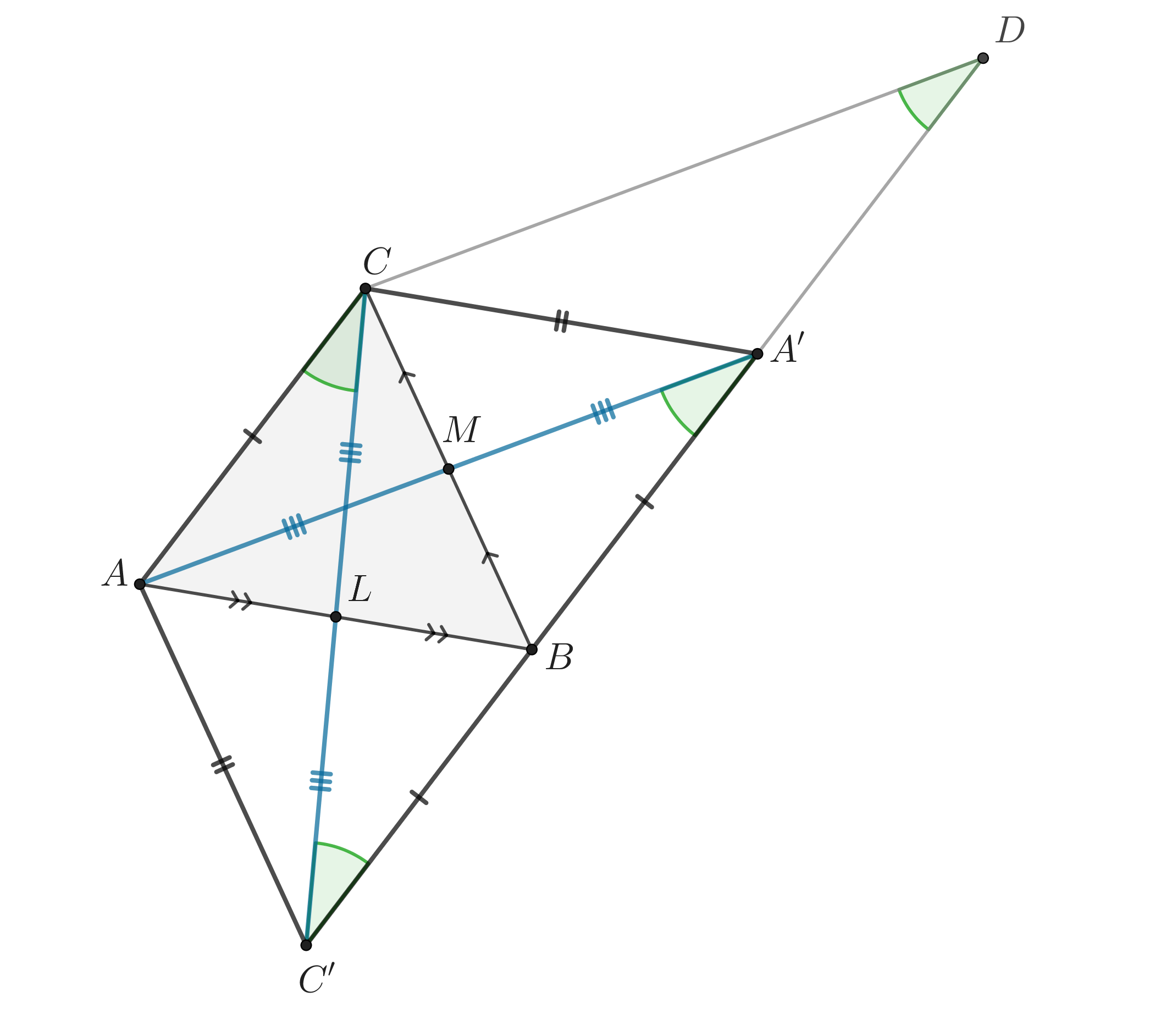
В треугольнике провели медиану
. Оказалось, что сумма углов
и
равна углу
. Найдите отношение медианы
к стороне
.
Продлим медиану за точку
на свою длину. Назовём полученную точку
.
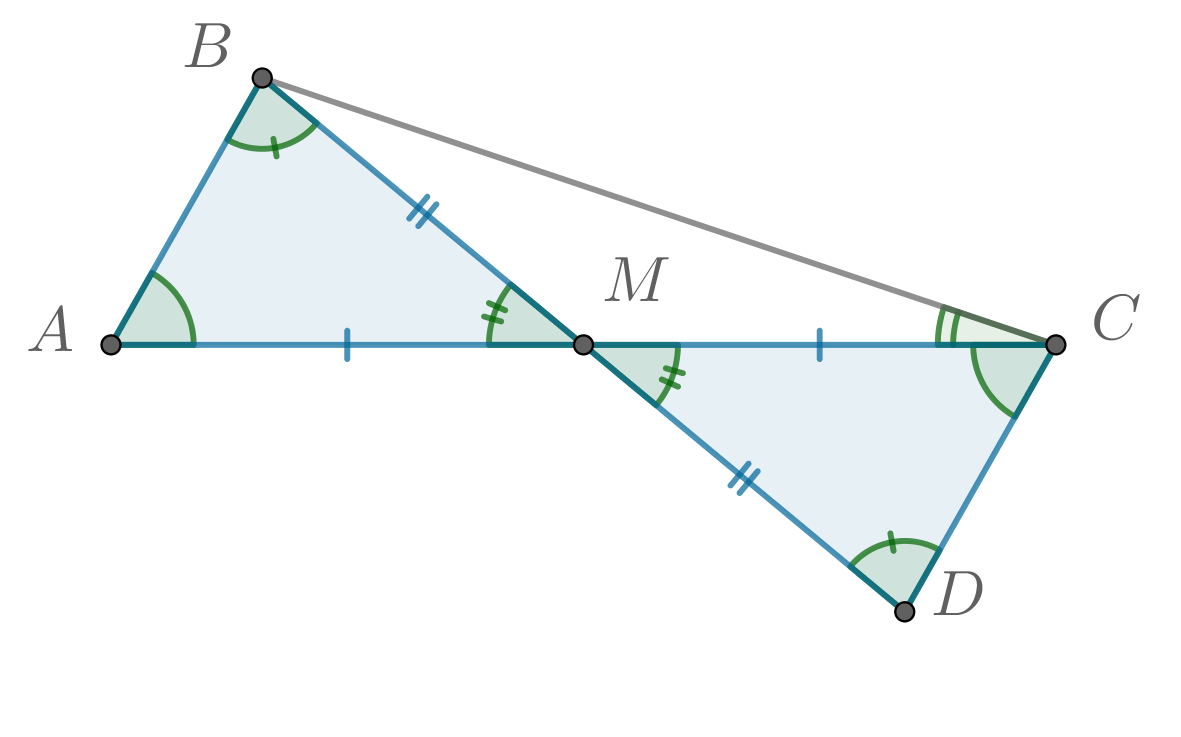
Рассмотрим треугольники и
. Они равны, так как
по построению,
по условию и
как вертикальные. В равных треугольниках соответственные элементы равны, в частности,
и
.
По условию , значит,
Таким образом, треугольник является равнобедренным, то есть
. Так как
, получаем, что
.
Ошибка.
Попробуйте повторить позже
В равностороннем треугольнике провели медианы
и
На медиане
отметили точку
так, что
а) Докажите, что описанная вокруг треугольника окружность делит
отрезок
в отношении
считая от вершины
б) Известно, что эта же окружность пересекает в точке
Ёe радиусы
и
пересекают медианы
и
в точках
и
Найдите
отношение
а)
1. Пусть медианы пересекаются в точке
По свойству данной точки
2. Раз и
то
— это середина отрезка
3. По определению — это средняя линия
которая параллельна
4. Проведём высоту в
лежит на высоте треугольника
следовательно,
и
5. Продлим до пересечения с
в точке
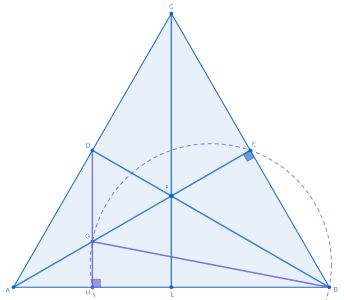
6. Поскольку и
— середина боковой стороны
то
— это
средняя линия
и
7. В равностороннем треугольнике высоты и медианы совпадают, стало быть,
— середина
откуда
8. Теперь нам осталось доказать, что — это и есть та самая точка
пересечения окружности и отрезка
(не считая точки
).
9. откуда
— вписанный и
—
действительно точка пересечения окружности с отрезком
Ч.Т.Д.
б)
1. Провед̈eм перпендикуляры и
на
и
соответственно.
2. Поскольку равносторонний, то
и
ещё и биссектрисы.
Таким образом,
3. По сумме углов
4. Вписанный и центральный
опираются на одну дугу, стало
быть
5. Поскольку то
—- вписанный и
6. как вертикальные.
то есть
7. поскольку
и
— перпендикуляры.
8. Из прошлых двух пунктов выводим подобие по двум
углам. Раз так, то
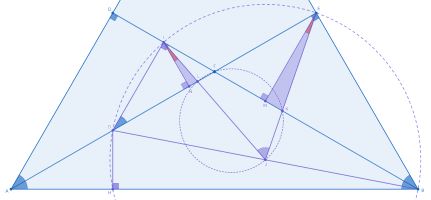
9. следовательно,
— диаметр и
10. и
— середина
стало быть
— средняя линия
11. Из прошлого пункта следует, что с коэффициентом
подобия
12.
Эти три тезиса в сумме
говорят о равенстве
13. Из прошлых двух пунктов следует, что с тем же
коэффициентом подобия
14. и
— высоты данных треугольников, следовательно, их длины
связаны тем же коэффициентом подобия
15. Из пунктов 14) и 8) следует, что
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На сторонах и
равностороннего треугольника
выбраны точки
и
соответственно так, что
. Точка
—
середина отрезка
. Докажите, что
.
Продлим медиану треугольника
на свою длину. Пусть мы получили точку
. Тогда
— параллелограмм, так как его
диагонали
и
точкой пересечения делятся пополам.
Тогда и
. Значит, соответственные углы
и
равны, то есть
.
Рассмотрим треугольник . В нем
и
, значит, этот треугольник является равносторонним, то есть
. Таким образом, точка
лежит на стороне
и
.
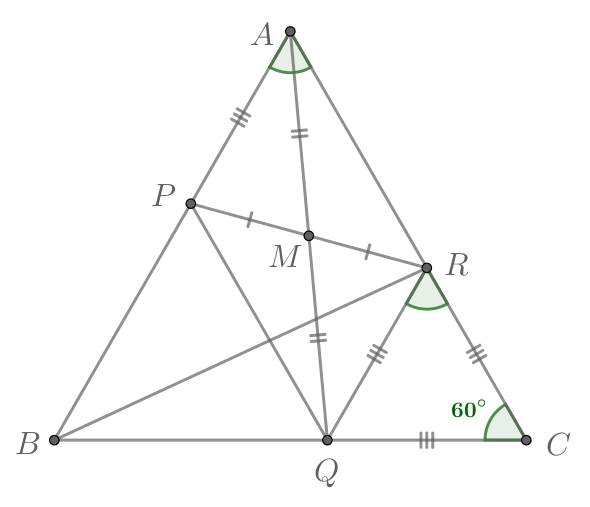
Рассмотрим треугольники и
. Они имеют общий угол
,
и
, значит,
по
первому признаку. В равных треугольниках соответственные элементы равны, в частности,
.
Ошибка.
Попробуйте повторить позже
В треугольнике проведена медиана
Точка
— середина отрезка
точка
— пересечение прямой
и
стороны
Известно, что
Докажите, что
Первое решение.
Пусть — точка, симметричная точке
относительно
Тогда
и
— параллелограмм (так как
диагонали четырехугольника
делят друг друга пополам).
![]()
В треугольнике стороны
и
равны, следовательно,
Кроме того,
как
вертикальные,
как накрест лежащие при параллельных прямых
и
и секущей
Треугольники и
равны по углу
и прилежащим к нему сторонам
следовательно,
Итого, получили следующую цепочку равенств углов
Тогда в треугольнике углы при вершинах
и
равны и
Второе решение.
Задачу можно решить без удвоения медианы, если обратить внимание на треугольники и
В этих треугольниках углы и
равны как дополняющие равные по условию углы
и
до
развернутого угла. Кроме того,
и
по условию.
Тогда треугольники и
равны по двум сторонам и углу между ними.
Отсюда лежащие напротив равных сторон углы и
равны и с привлечением равных вертикальных углов
и
получаем равные углы в треугольнике
и требуемое равенство
Ошибка.
Попробуйте повторить позже
В треугольнике медиана
в четыре раза меньше стороны
и образует с ней угол
. Найдите угол
.
Пусть — точка, симметричная точке
относительно
. Тогда
и
— параллелограм (так как диагонали делят
друг друга пополам).
Пусть — середина
.
,
. Получаем, что в треугольнике
угол
равен
и
, следовательно, он равносторонний и
.
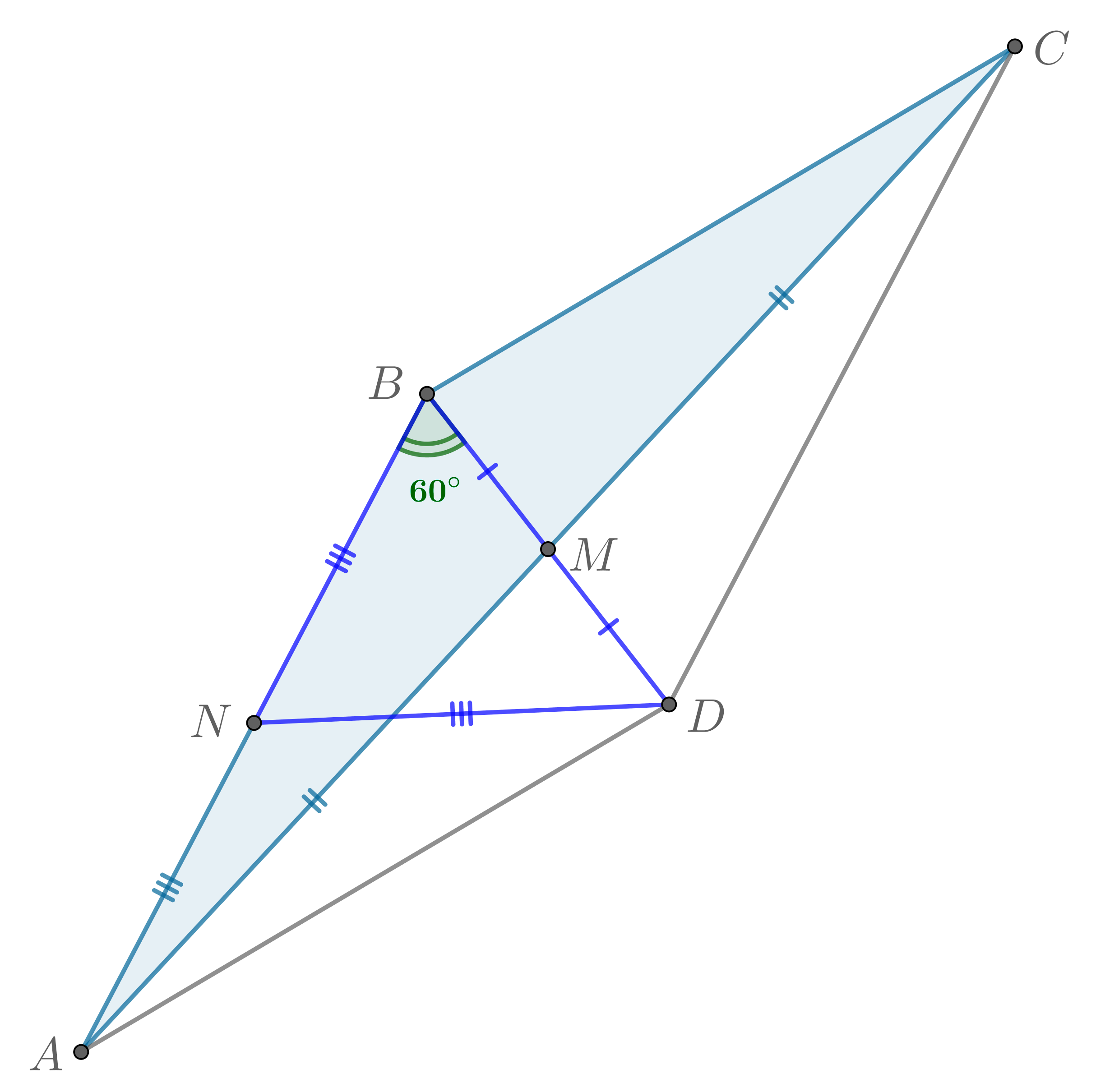
Тогда в треугольнике медиана
равна половине стороны
, к которой она проведена, следовательно, он прямоугольный с
прямым углом
.
, следовательно,
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
во вне построили квадраты
и
Докажите, что отрезок
в два раза
больше медианы
треугольника
Пусть — точка, симметричная точке
относительно
. Тогда
и
— параллелограм, так как диагонали
и
точкой пересечения делят друг друга пополам.
![]()
Обозначим . Из параллельности
и
следует, что
.
Выразим через
:
Отсюда получаем и треугольники
и
равны по двум сторонам и углу между ними. Из равенства
треугольников имеем искомое соотношение
.
Доказательство
Ошибка.
Попробуйте повторить позже
В треугольнике равны две медианы. Докажите, что он равнобедренный.
Пусть в равны медианы
и
. Докажем, что
.
Продлим эти медианы на отрезки и
, равные
и
соответственно. Получим два параллелограмма
и
. Следовательно,
,
, откуда
,
и
лежат на одной прямой, то есть
.
как накрест лежащие при
и секущей
. Также
. Проведем через точку
прямую, параллельную
и пересекающую прямую
в точке
. Тогда
— равнобедренный (
как
противоположные стороны параллелограмма
, значит,
), следовательно,
.
как соответственные при
и секущей
. Тогда
. Следовательно,
по
,
и
. Значит, равны третьи стороны
. Ч.т.д.
Ошибка.
Попробуйте повторить позже
выпуклом четырехугольнике
стороны
и
paвны,
— середина стороны
Известно, что угол
равен
Найдите угол между диагоналями четырехугольника
Обозначим точку пересечения диагоналей через .
и
— точки, симметричные относительно
точкам
и
соответственно.
Тогда
,
по построению.
— параллелограмм (т.к. диагонали делят друг друга пополам), следовательно,
.
— параллелограмм (т.к. диагонали делят друг друга пополам), следовательно,
.
— параллелограмм (т.к. диагонали делят друг друга пополам), следовательно,
.
Треугольники и
равны как прямоугольные по двум катетам (
общий,
по построению),
следовательно их гипотенузы равны
. Получили, что
и треугольник
— равносторонний.
![]()
Рассмотрим искомый угол . С одной стороны, из параллельности
и
он равен углу
. С другой стороны, как
внешний для треугольника
он равен сумме углов
. Треугольники
и
равнобедренные, следовательно,
. Подытоживая написанные равенства, получаем
Треугольники и
равны по трем сторонам (
,
), следовательно,
.
Тогда, подставив в равенство выше, получим
, причем
, т.к.
треугольник
равносторонний. Таким образом, искомый угол
.
Ошибка.
Попробуйте повторить позже
Про выпуклый пятиугольник известно, что
и
Докажите,
что сторона
в два раза больше медианы
треугольника
Проблема.
В задаче есть дурацкое условие про то, что сумма каких-то двух углов равна третьему, с которым непонятно, что делать.
Естественная мысль.
Какой еще угол равен сумме двух углов из условия? Внешний угол при вершине треугольника
.
Пусть — точка, симметричная точке
относительно
. Угол
— внешний в треугольнике
, тогда
. Треугольники
и
равны по углу при вершине
и прилежащим к
ней сторонам (
), следовательно, их третьи стороны тоже равны
. Точка
—
середина
, точка
— середина
, значит,
средняя линия треугольника
и
.
![]()



