Ошибка.
Попробуйте повторить позже
В основании прямой призмы лежит треугольник с прямым углом
Точки
и
— середины ребер
и
соответственно, точка
является точкой пересечения диагоналей грани
Точка
делит ребро
в отношении
считая от вершины
Докажите, что прямые
и
скрещиваются.
![]()
Рассмотрим плоскость . По признаку, чтобы прямые скрещивались, нужно
чтобы первая прямая пересекала плоскость, где лежит вторая прямая, в точке, не
лежащей на второй прямой. Иными словами, нужно доказать, что точка
не
лежит в плоскости
, то есть что прямая
пересекает
(где
лежит прямая
) в точке
, не лежащей на
. Введём систему координат,
как показано на рисунке. Пусть ось
вдоль
, ось
вдоль
, ось
вдоль
(так как
перпендикулярно основанию (боковое ребро прямой
призмы), угол между
и
равен
. Пусть
.
Тогда:
Запишем уравнение плоскости . Составим
систему:
|
|
Пусть . Тогда:
|
|
|
|
Подставим в уравнение плоскости координаты точки
и проверим,
принадлежит ли она плоскости (не должна):
Значит точка не лежит в
, а значит прямые
и
скрещиваются.
Ошибка.
Попробуйте повторить позже
Точки являются вершинами
прямоугольника
Найдите меньший угол между диагоналями
прямоугольника.
Пусть — наименьший угол между диагоналями прямоугольника.
Найдём косинус угла между ними через скалярное произведение:
Получили, что косинус угла отрицательный, а значит угол тупой. Так как
нам нужно найти наименьший угол между диагоналями, берём смежный с ним и
получаем:
, следовательно,
Ошибка.
Попробуйте повторить позже
В пирамиде с вершиной
проведена высота
Найдите
координаты точки
если известны координаты вершин пирамиды:
Посчитаем длины боковых рёбер пирамиды:
Значит, у пирамиды равны боковые рёбра, следовательно, точка является
центром описанной около основания окружности.
Определим тип треугольника с помощью теоремы косинусов. Для этого найдем
косинус угла, лежащего напротив наибольшей стороны треугольника, то есть
напротив
Таким образом, треугольник в основании — прямоугольный, причем —
центр описанной окружности. Тогда
является серединой гипотенузы
то
есть
Ошибка.
Попробуйте повторить позже
Точки являются
вершинами пирамиды
Найдите координаты основания биссектрисы
лежащей в грани
Рассмотрим треугольник Найдём его стороны.
Получается, что треугольник равнобедренный и биссектриса
также является медианой. Тогда
— середина
и
Ошибка.
Попробуйте повторить позже
Дан цилиндр, — диаметр его верхнего основания, на окружности
нижнего основания взята произвольная точка
Точка
— проекция
точки
на нижнее основание, точка
на отрезке
такова, что
Прямая
пересекает боковую поверхность цилиндра
в точке
Найдите длину отрезка
если высота цилиндра равна
4.
Рассмотрим плоскость Она пересекает боковую поверхность цилиндра по
отрезкам
и
где
— проекция точки
на плоскость верхнего
основания. Так как
то
— параллелограмм.
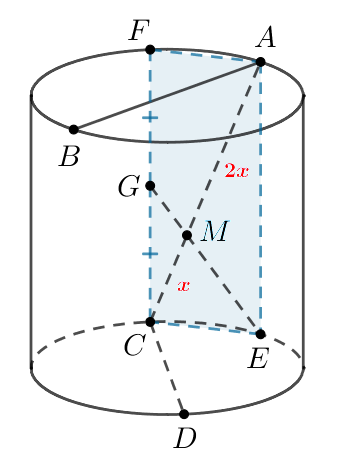
Тогда пересекает
в точке
Получаем два подобных треугольника
и
как вертикальные,
как
накрест лежащие при
и секущей
Из подобия имеем:
Ошибка.
Попробуйте повторить позже
Дан цилиндр, — диаметр его верхнего основания, а
— диаметр его
нижнего основания. Точка
— середина отрезка
точка
—
проекция точки
на нижнее основание цилиндра. Докажите, что точка
пересечения прямой
с поверхностью цилиндра лежит в плоскости верхнего
основания.
Рассмотрим плоскость Она пересекает боковую поверхность цилиндра по
отрезкам
и
где
— проекция точки
на плоскость верхнего
основания.
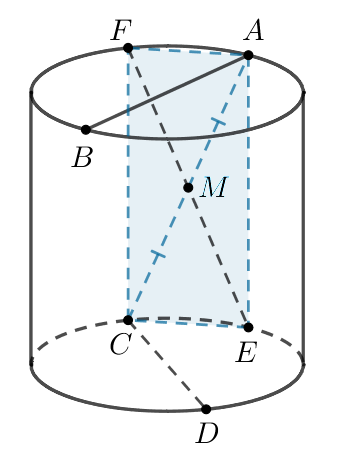
Так как
то
— параллелограмм, следовательно,
его диагонали точкой пересечения делятся пополам. Значит, диагональ
пересекает диагональ
в точке
то есть
— точка пересечения прямой
с плоскостью верхнего основания.
Ошибка.
Попробуйте повторить позже
Дан цилиндр, — диаметр его верхнего основания, а
— диаметр его
нижнего основания, причем
Радиус основания цилинда равен 1, высота
равна 4. Найдите длину отрезка
Пусть и
— проекции точек
и
на нижнее основание цилиндра. Тогда

Рассмотрим прямоугольный треугольник В нем имеем:
Отрезок найдем из прямоугольного равнобедренного
в
котором
Тогда и окончательно получаем:
Ошибка.
Попробуйте повторить позже
Непересекающиеся диагонали двух смежных граней прямоугольного параллелепипеда
наклонены к плоскости основания под углами и
Найдите угол
между
этими диагоналями.
Пусть
Тогда
Тогда
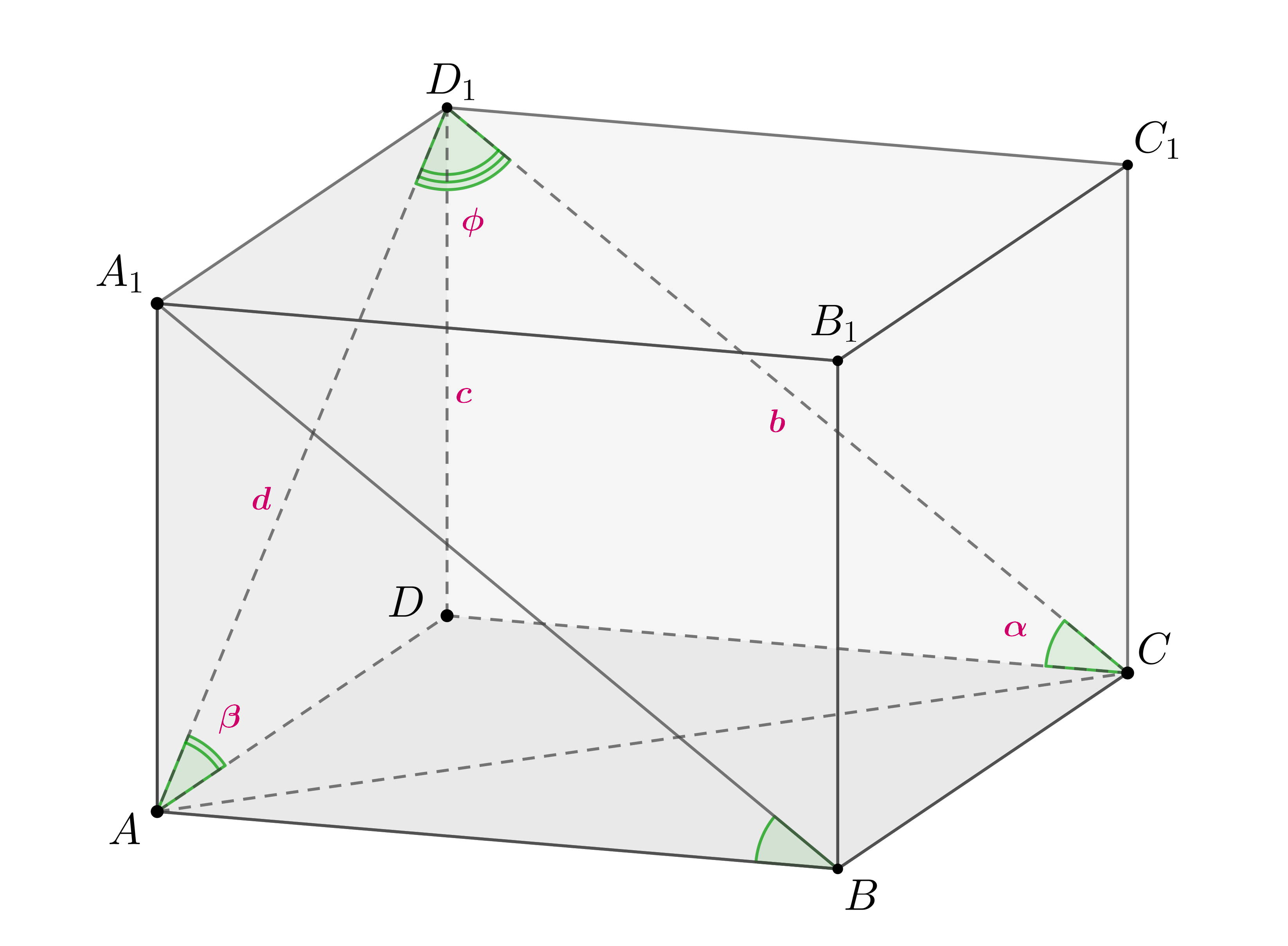
По теореме косинусов для
Так как
то
Ошибка.
Попробуйте повторить позже
Даны параллелограмм и трапеция
с основанием
, не лежащие в одной плоскости. а) Выясните
взаимное расположение прямых
и
б) Найдите периметр трапеции, если известно, что в нее можно вписать
окружность и
см,
см.
а) .
б) В описанном четырехугольнике суммы пар противоположных стороны равны, т.е. , тогда
периметр трапеции равен
![]()
б) 100 см
Ошибка.
Попробуйте повторить позже
На скрещивающихся прямых и
отмечены соответственно точки
и
Через прямую
и точку
проведена плоскость
, а через прямую
и точку
— плоскость
а) Лежит ли прямая
в плоскости
?
б) Пересекаются ли плоскости
и
? При положительном ответе укажите прямую, по которой они
пересекаются.
а) По условию . Если бы
тоже лежала в
, возникало бы противоречие с тем, что
и
скрещиваются.
б) По условию , кроме того,
. По условию
, кроме того,
. Получили, что обе
точки
и
принадлежат обеим плоскостям
и
, следовательно, пересечением плоскостей является прямая
.
Ошибка.
Попробуйте повторить позже
Прямая пересекает сторону
треугольника
Каково взаимное расположение прямых
и
если:
а) прямая лежит в плоскости
и не имеет общих точек с отрезком
б) прямая не лежит в плоскости
а) Пусть — точка пересечения
и
Очевидно, что если бы
была параллельна
то она бы пересеклась с
отрезком
что противоречит условию пункта а). Значит,
и
пересекаются.
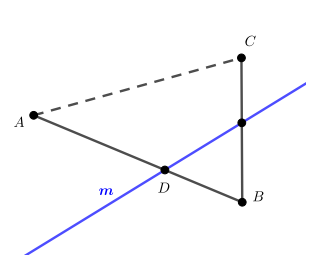
б) Пусть — точка пересечения
и
Допустим, что
и
не скрещиваются. Тогда они однозначно
задают некоторую плоскость
Точки
и
лежат в
тогда и
лежит в
так как точки
и
лежат на одной прямой. Получили, что точка
прямая
и прямая
лежат в одной плоскости, что
противоречит условию пункта б) «прямая
не лежит в плоскости
». Значит,
и
скрещивающиеся.
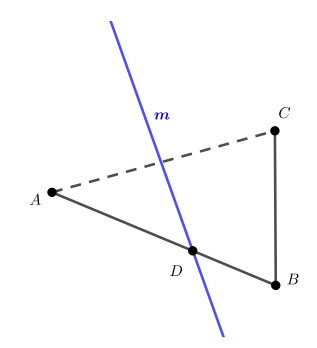
а) и
пересекаются
б) и
скрещиваются
Ошибка.
Попробуйте повторить позже
Точка не лежит в плоскости треугольника
, точки
и
— середины отрезков
и
соответственно, точка
лежит на отрезке
Выясните взаимное расположение прямых: a)
и
б)
и
в)
и
г)
и
д)
и
e)
и
.
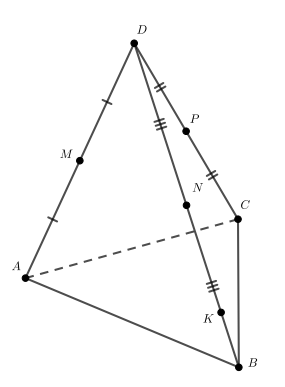
а) Прямая совпадает с прямой
, следовательно,
и
пересекаются.
б) Точки лежат в плоскости треугольника
, следовательно, прямые
и
пересекаются,
либо параллельны.
как средняя линия в треугольнике
, точки
и
по условию не совпадают,
следовательно,
и
пересекаются.
в) как средняя линия в треугольнике
.
г) как средняя линия в треугольнике
.
д) Прямая совпадает с прямой
, точка
не лежит в плоскости
по условию, следовательно,
прямые
и
не лежат в одной плоскости — они скрещиваются.
е) Прямая совпадает с прямой
, точка
не лежит в плоскости
по условию, следовательно,
прямые
и
не лежат в одной плоскости — они скрещиваются.
Ошибка.
Попробуйте повторить позже
Точка лежит на отрезке
. Через точку
проведена плоскость, а через точки
и
— параллельные
прямые, пересекающие эту плоскость в точках
и
соответственно.
Найдите длину отрезка , если:
а) точка — середина отрезка
и
;
б) и
.
Прямые и
параллельны, а значит, однозначно задают плоскость. Точка
также лежит в этой плоскости,
так как она лежит на прямой
. Фактически мы теперь имеем дело с плоской задачей в плоскости
.
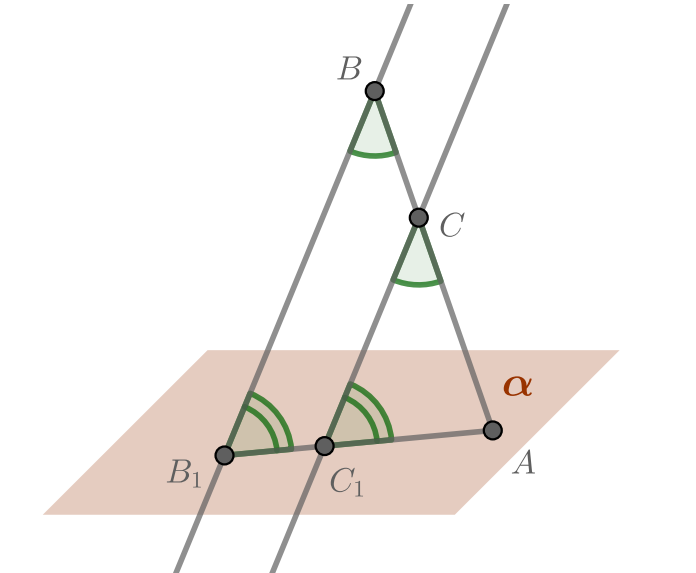
а) Если — середина
, то
— средняя линия в треугольнике
.
Тогда имеем
б) Из параллельности следует, что с коэффициентом
Тогда имеем
Ошибка.
Попробуйте повторить позже
На рисунке точки
и
— середины отрезков
и
Найдите периметр четырехугольника
если
![]()
Так как и
— средние линии в треугольниках
и
соотвественно, то
Аналогично
Тогда — параллелограмм по определению, откуда
Отсюда периметр равен



