Ошибка.
Попробуйте повторить позже
Представьте функции в кусочно-заданном виде. Найдите “вершину” графика каждой функции и определите траекторию движения этой точки:
2.1.
2.2.
2.3.
2.4.
2.1.
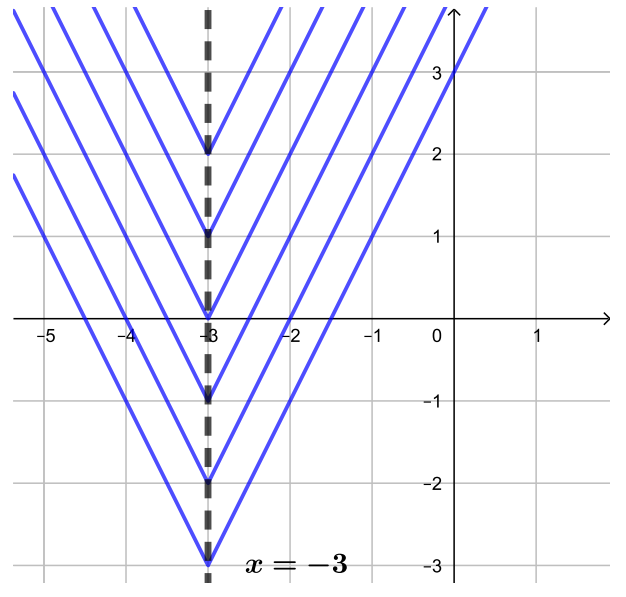
Это график уголка модуля, с вершиной в точке , растянутый вдвое вдоль оси ординат. В зависимости от
вершина может находиться в произвольной точке прямой
, это и будет траекторией вершины.
2.2.
Представим функцию в следующем виде . Ее график — уголок модуля
с вершиной в точке
. Найдем траекторию вершины
Получили, что вершина уголка может лежать в произвольной точке параболы .
![]()
2.3.
Это корыто с наклонным дном, углы которого находятся в точках и
.
![]()
2.4.
При функция обращается в
. Для
представим функцию в виде
.
Ее график — уголок модуля с вершиной в точке
с ветвями вниз, растянутый вдоль оси ординат в
раз. Найдем траекторию вершины (помним, что
)
Получили, что вершина уголка может лежать в произвольной точке гиперболы .
![]()
Ошибка.
Попробуйте повторить позже
Постройте при помощи элементарных преобразований (сдвиг, сжатие/растяжение, отражение), где это возможно, графики следующих функций/уравнений:
1.1.
1.2.
1.3.
1.4.
1.5.
1.1.
| y = x2 |
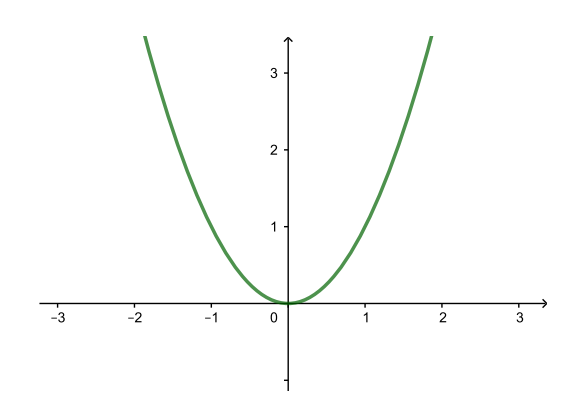
| y = (x − 3)2 (→ на 3) |
![]()
| y = (x − 3)2 + 1 (↑ на 1) |
![]()
1.2.
| y = |x| |
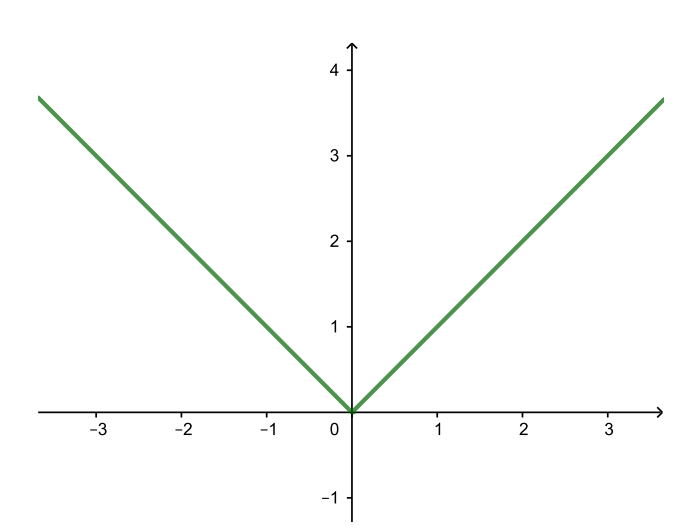
| y = |x − 2| (→ на 2) |
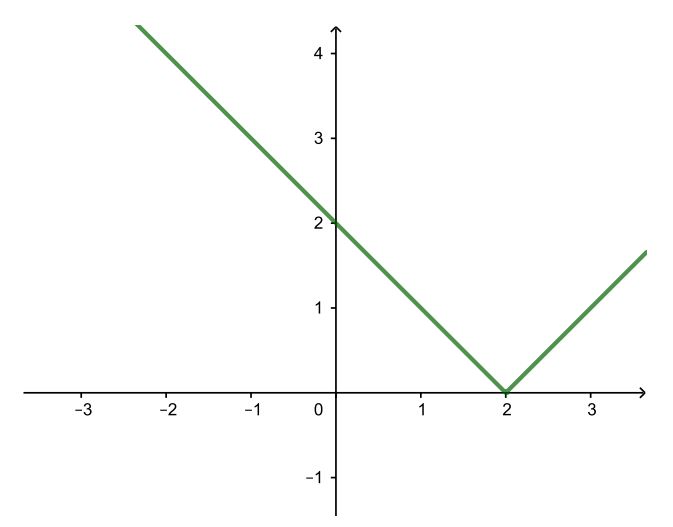
| y = 2|x − 2| (растяжение вдоль Oy) |
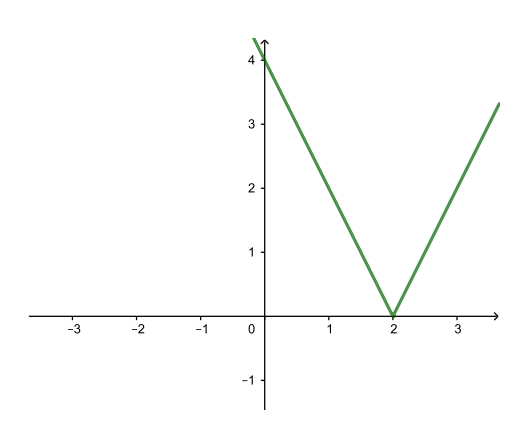
| y = −2|x − 2| (симметрия относительно Ox) |
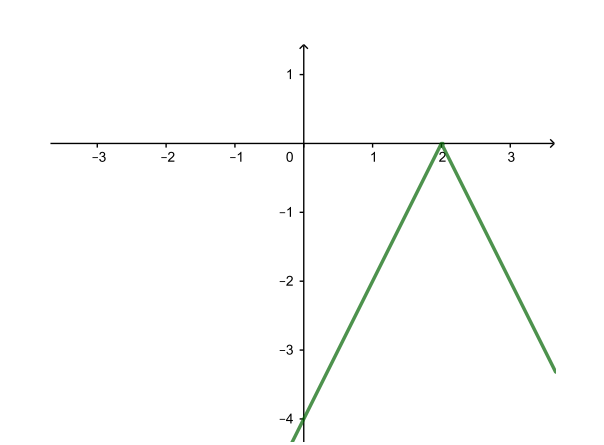
1.3.
| y = x2 |
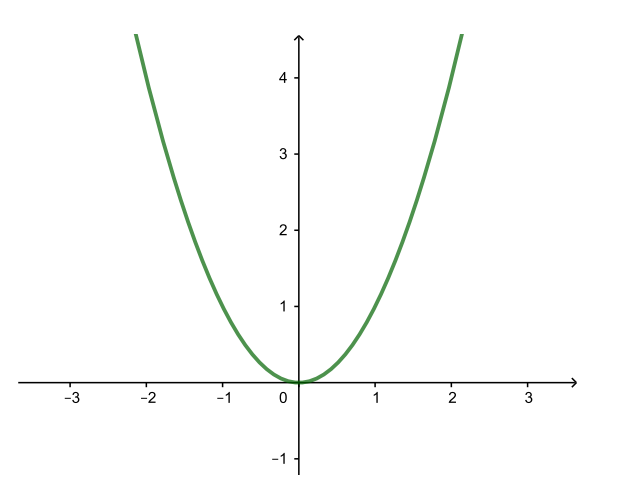
| y = (x + 1)2 (← на 1) |
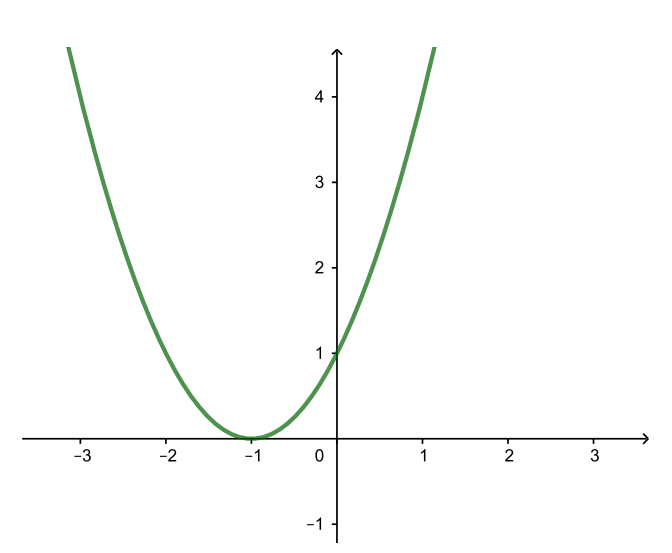
| y = (x + 1)2 + 3 (↑ на 3) |
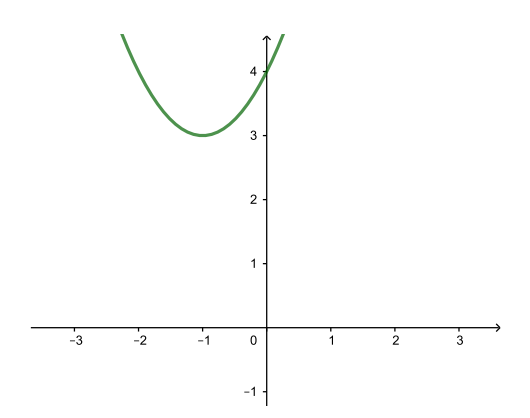
1.4.
| y = x2 |

| y = (x + 1,5)2 (← на 1,5) |
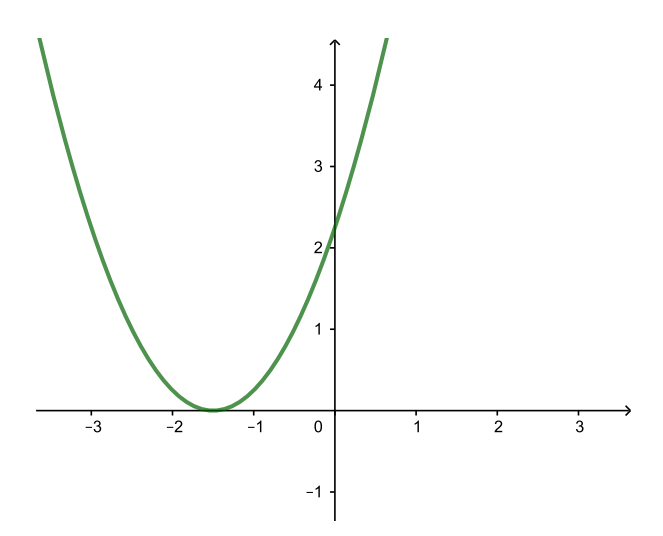
| y = (x + 1,5)2 − 2,25 (↓ на 2,25) |
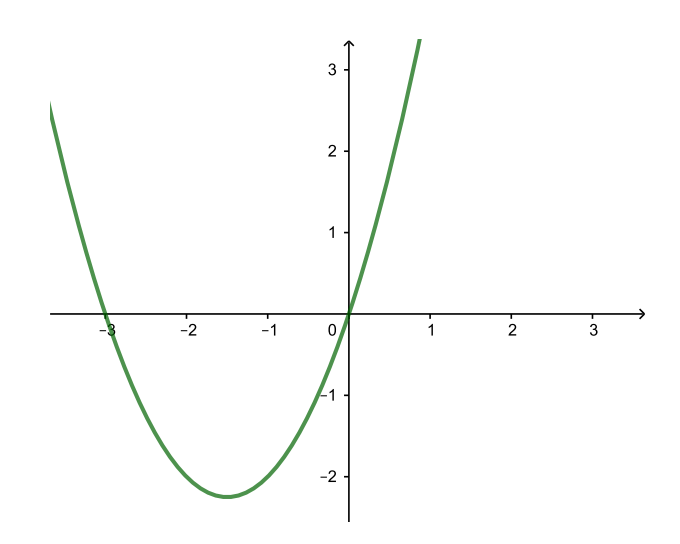
| y = 2((x + 1,5)2 − 2,25) (растяжение вдоль оси Oy) |
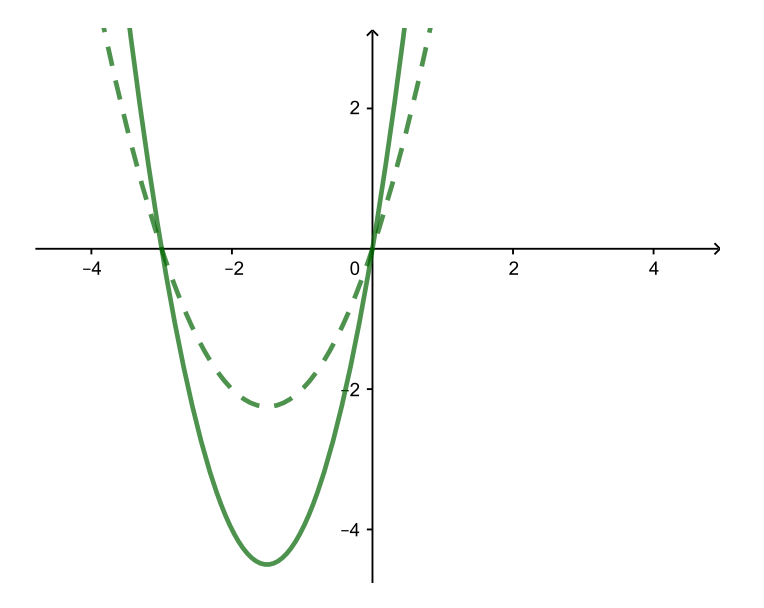
| y = −2((x+1,5)2−2,25) (симметрия относительно оси Ox) |
![]()
1.5.
| y = x2 |

| y = (x + 0,5)2 (← на 0,5) |
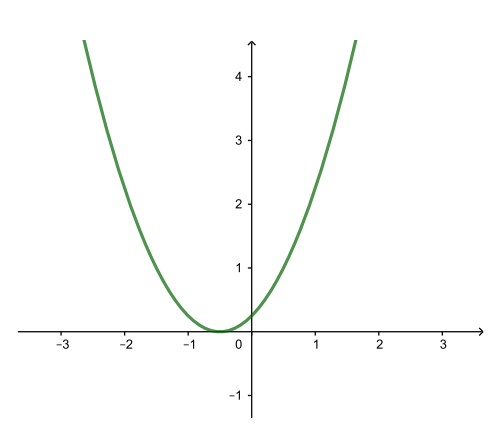
| y = 4(x + 0,5)2 (растяжение вдоль оси Oy) |
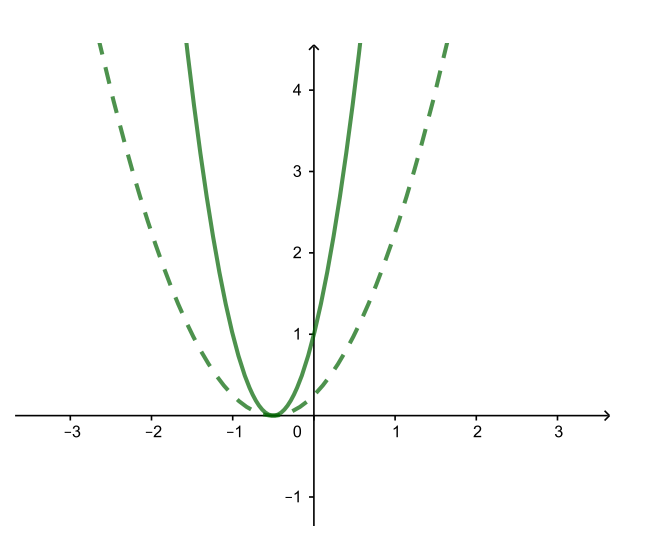
| y = 4(x + 0,5)2 − 2 (↓ на 2) |
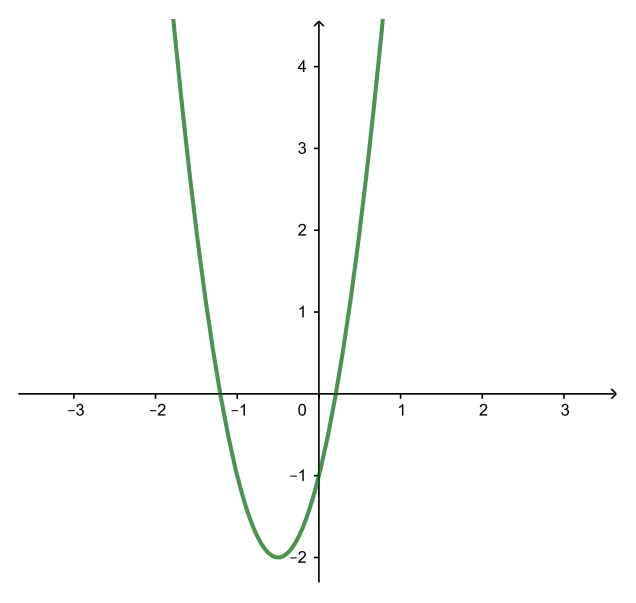
| y = 4(|x|+0,5)2−2 (стираем все, что левее оси Oy, и отражаем туда все, что правее нее) |
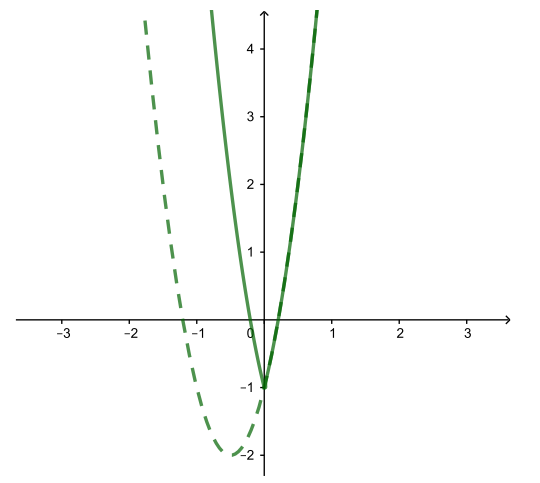
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
имеет ровно два решения?
Обозначим График
— это сдвинутая на
вверх парабола
с ветвями вниз. При этом часть
параболы, лежащая ниже оси
отражена в верхнюю полуплоскость.
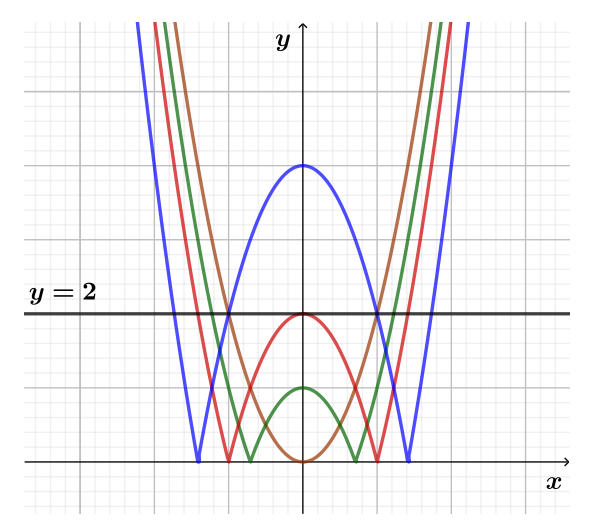
Заметим, что вершина нашей параболы всегда имеет неотрицательную координату по оси
а значит, не будет
отражена.
При условии, что вершина лежит ниже прямой то есть
график функции
будет иметь ровно две точки
пересечения с прямой
— с ней пересечется каждая из отраженных ветвей. Если же
то точек пересечения будет
три или четыре.
Тогда найдем подходящие значения параметра:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Выполнен обоснованный переход к неравенству, которое может отличаться от верного знаком неравенства | 2 |
| ИЛИ | |
| Неравенство составлено верно, но допущена ошибка в его решении | |
| Верно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
При каких значениях параметра графики функций
имеют три общие точки.
Графиком функции является парабола, ветви которой направлены вверх, и которая имеет
либо одну точку пересечения с осью абсцисс (если
), либо две точки пересечения с осью абсцисс:
и
(если
).
При функции принимают вид:
и
. Для того, чтобы найти точки
пересечения графиков функций, можно решить уравнение
. Это уравнение имеет один корень,
следовательно,
не подходит.
Пусть . Значит, графиком
является:
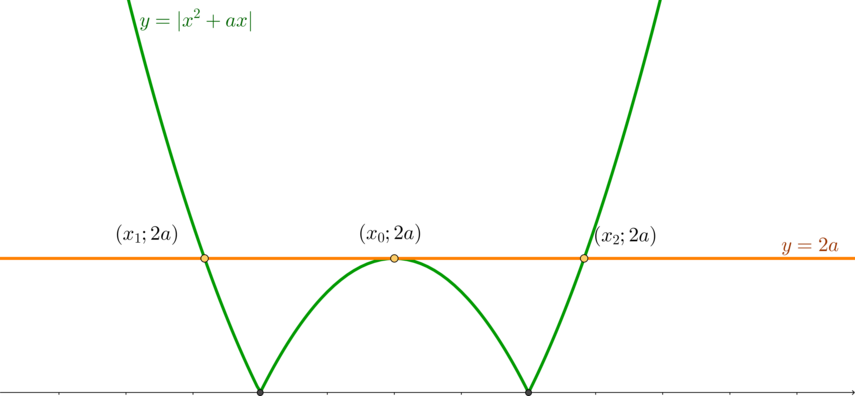
Для того, чтобы графики функций имели три общие точки, необходимо, чтобы прямая
выглядела, как показано на рисунке, то есть проходила через вершину
параболы
. Значит:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет хотя бы одно решение.
Сделаем замену ,
,
,
, тогда система примет вид
- 1.
- Пусть
. Тогда система имеет вид
Такая система имеет решения, как минимум
,
, следовательно,
нам подходит.
- 2.
- Пусть
. Тогда можно разделить первое уравнение на второе и получить новую систему
Так как
не является решением этого уравнения.
представляет собой пучок прямых, проходящих через точку
, а
представляет собой гиперболу. Найдем те
, при которых прямая
имеет хотя бы одну точку пересечения с гиперболой
, причем абсцисса этой точки
- 2.1.
, тогда графически все выглядит следующим образом:
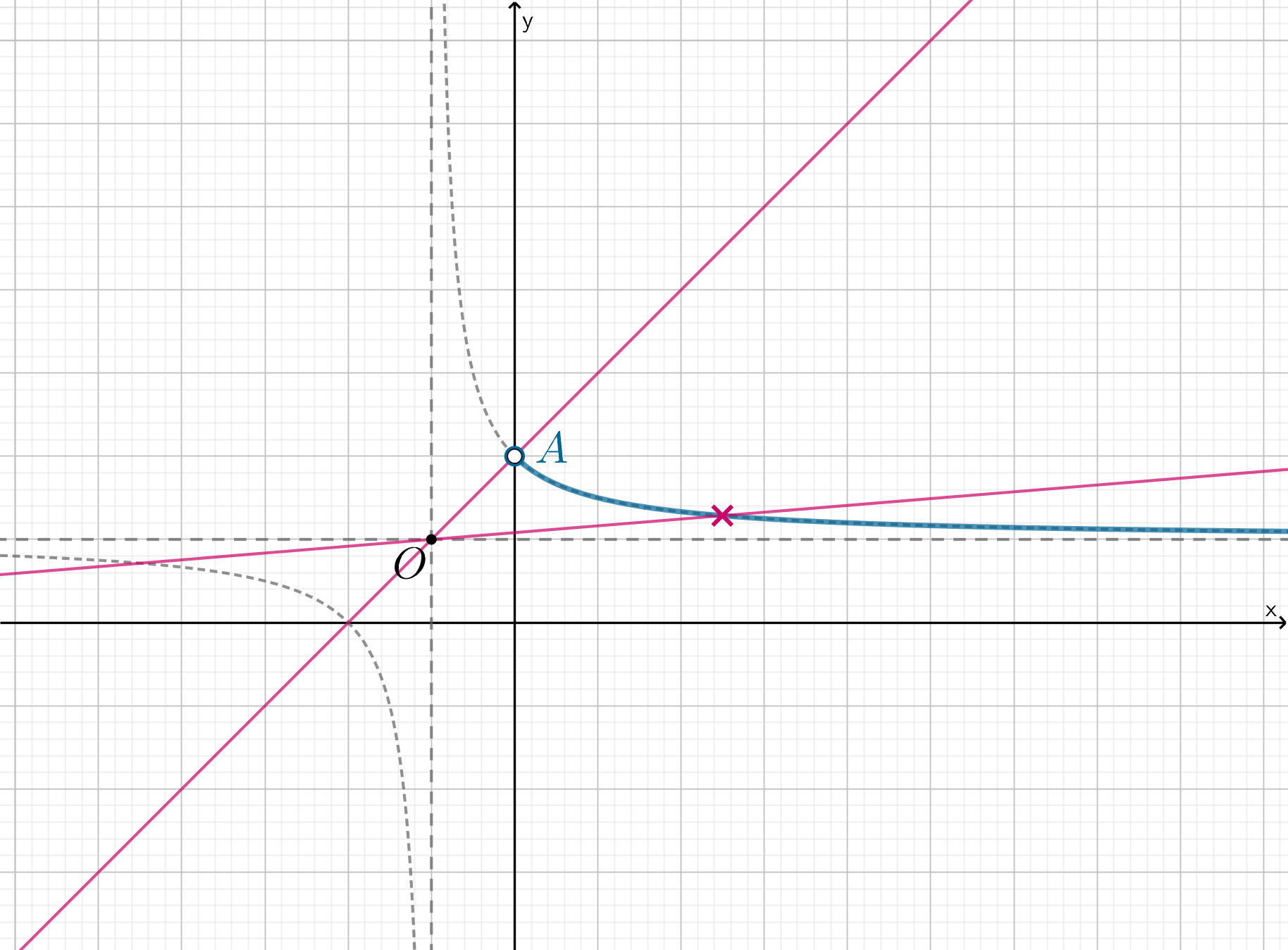
Нам подходят все прямые, у которых угловой коэффициент
и меньше, чем у прямой, проходящей через точку
. Координаты точки
равны
, следовательно, прямая проходит через
при
Следовательно, условию
в этом случае соответствуют
- 2.2.
, тогда графически все выглядит следующим образом:
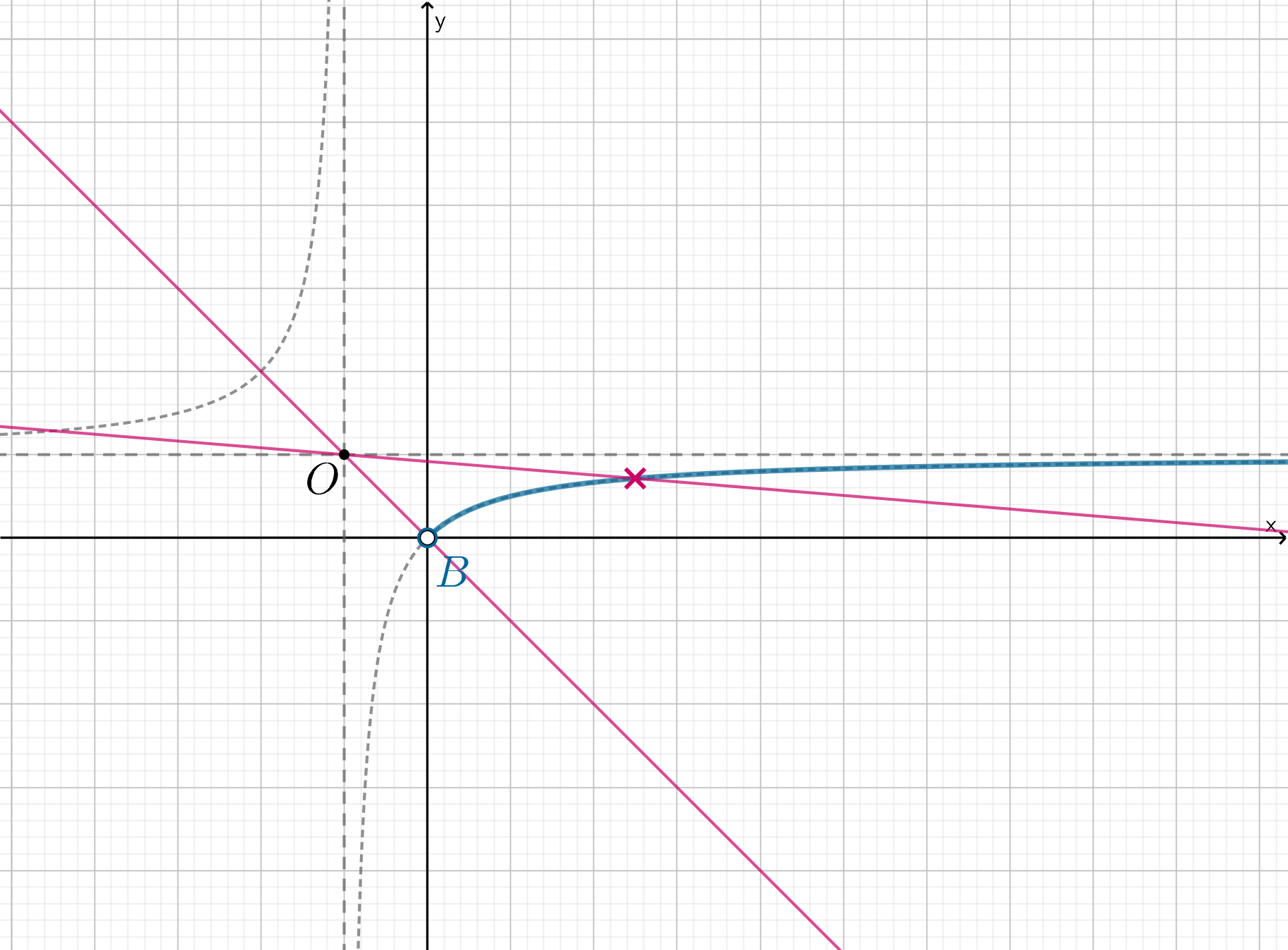
Нам подходят все прямые, у которых угловой коэффициент
и больше, чем у прямой, проходящей через точку
. Следовательно, прямая проходит через
при
Следовательно, условию
в этом случае соответствуют
Тогда ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет ровно два различных решения.
Система равносильна
Будем искать точки пересечения прямой (это равенство задает пучок прямых, проходящих через начало координат) со
множеством
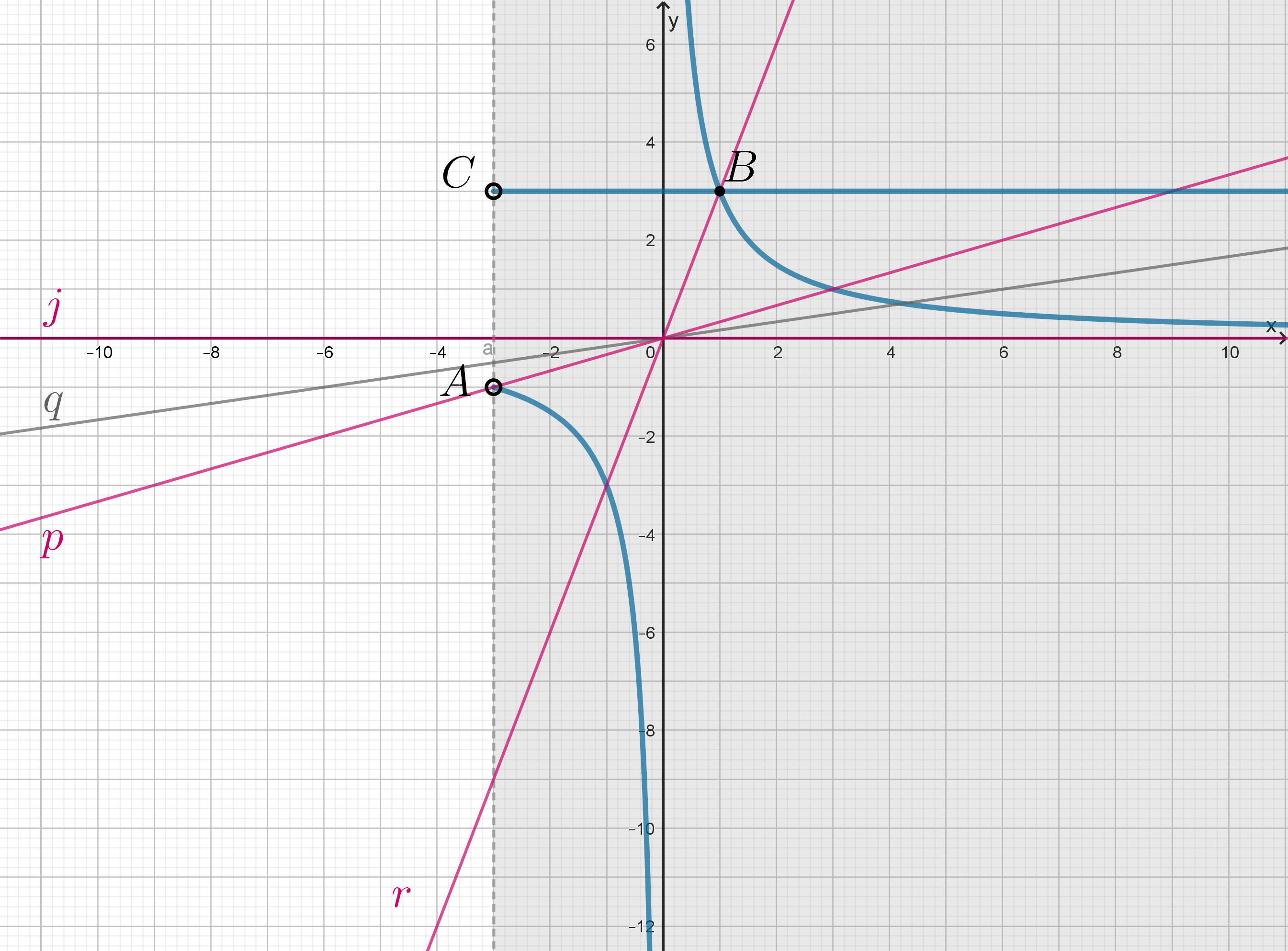
,
.
Когда прямая находится между положениями и
(включая
), а также в положении
, то графики имеют две точки
пересечения.
;
;
.
Следовательно, и
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
не имеет решений? При каких уравнение имеет решения и все решения принадлежат отрезку
Рассмотрим две функции:
График представляет собой уголок, вершина которого имеет координаты
следовательно, движется по
параболе
Найдем точки пересечения прямой
с траекторией
Точка на прямой абсцисса которой равна
имеет ординату
то есть
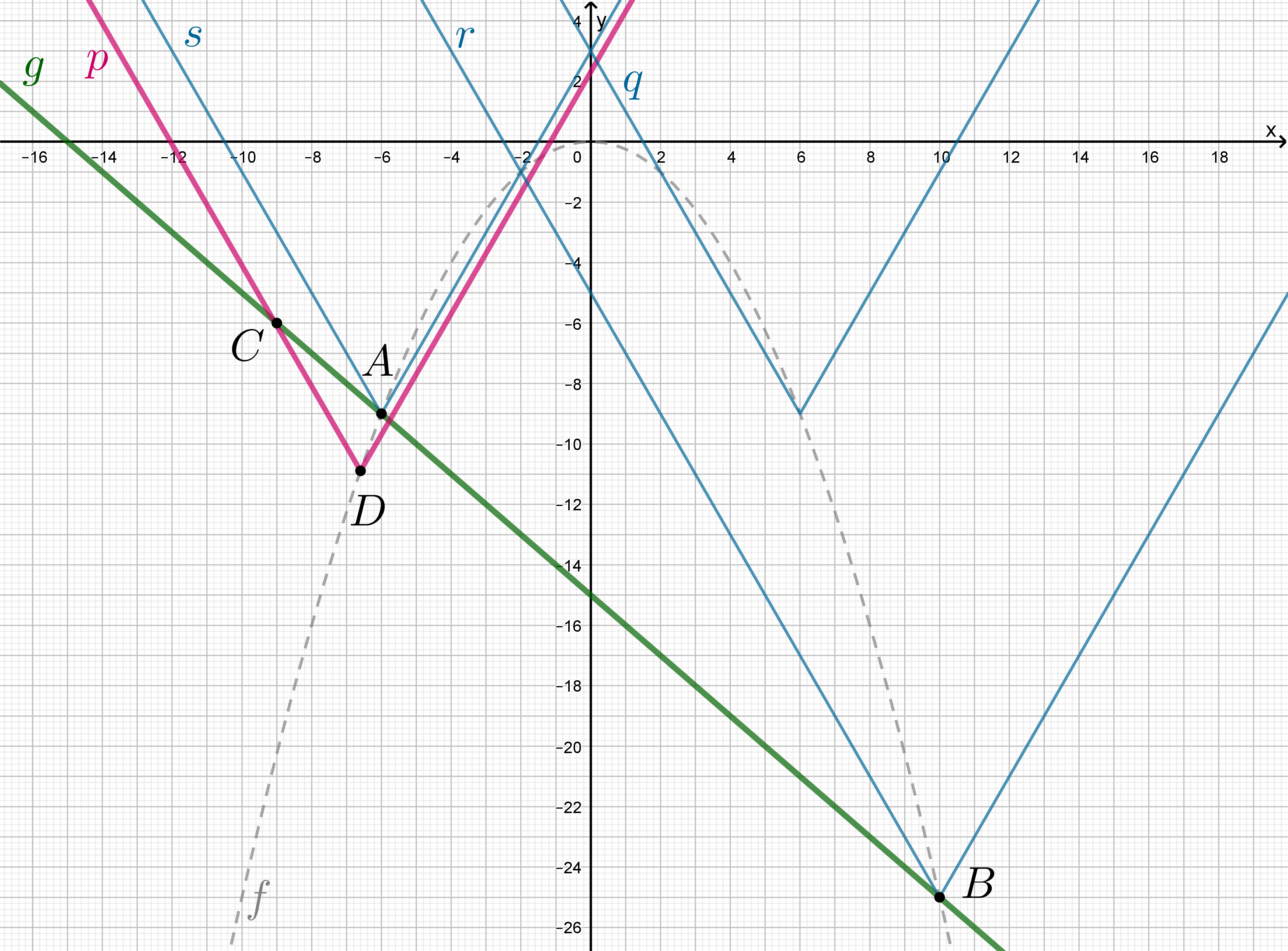
Если вершина уголка перемещается по параболе от точки
до точки
не включая эти положения, то уравнение не
имеет решений, так как уголок находится выше прямой и не имеет с ней точек пересечения. Следовательно, нет решений при
то есть при
Если — такая позиция вершины
что левая ветвь уголка проходит через точку
то это граничное положение, при
котором есть решения и эти решения из отрезка
Все положения от
до
нам также подходят плюс подходит
положение, когда вершина
находится в точке
Левая ветвь уголка задается уравнением следовательно, она проходит через
если
В нашем случае речь идет о значениях параметра так как
соответствует положению, когда
вершина
находится ниже точки
на параболе.
Следовательно, при и
уравнение имеет решения и все они из отрезка
— нет решений
— все решения из отрезка
Ошибка.
Попробуйте повторить позже
Найдите все значения , при которых уравнение
имеет три различных решения.
Преобразуем уравнение
Рассмотрим функции ,
,
на области
. На этой области объединение графиков
и
представляет собой четырехугольник, диагональ
которого равна
и лежит на прямой
.
Заметим, что . Значит, из
следует, что
, следовательно, расстояние между двумя точками на параболе,
ординаты которых равны
, равно
. Значит, когда левая ветка параболы проходит через точку
, то правая еще не доходит то
точки
. И аналогично наоборот. Следовательно, три решения будет, когда либо левая ветка проходит через
, либо правая проходит
через
:
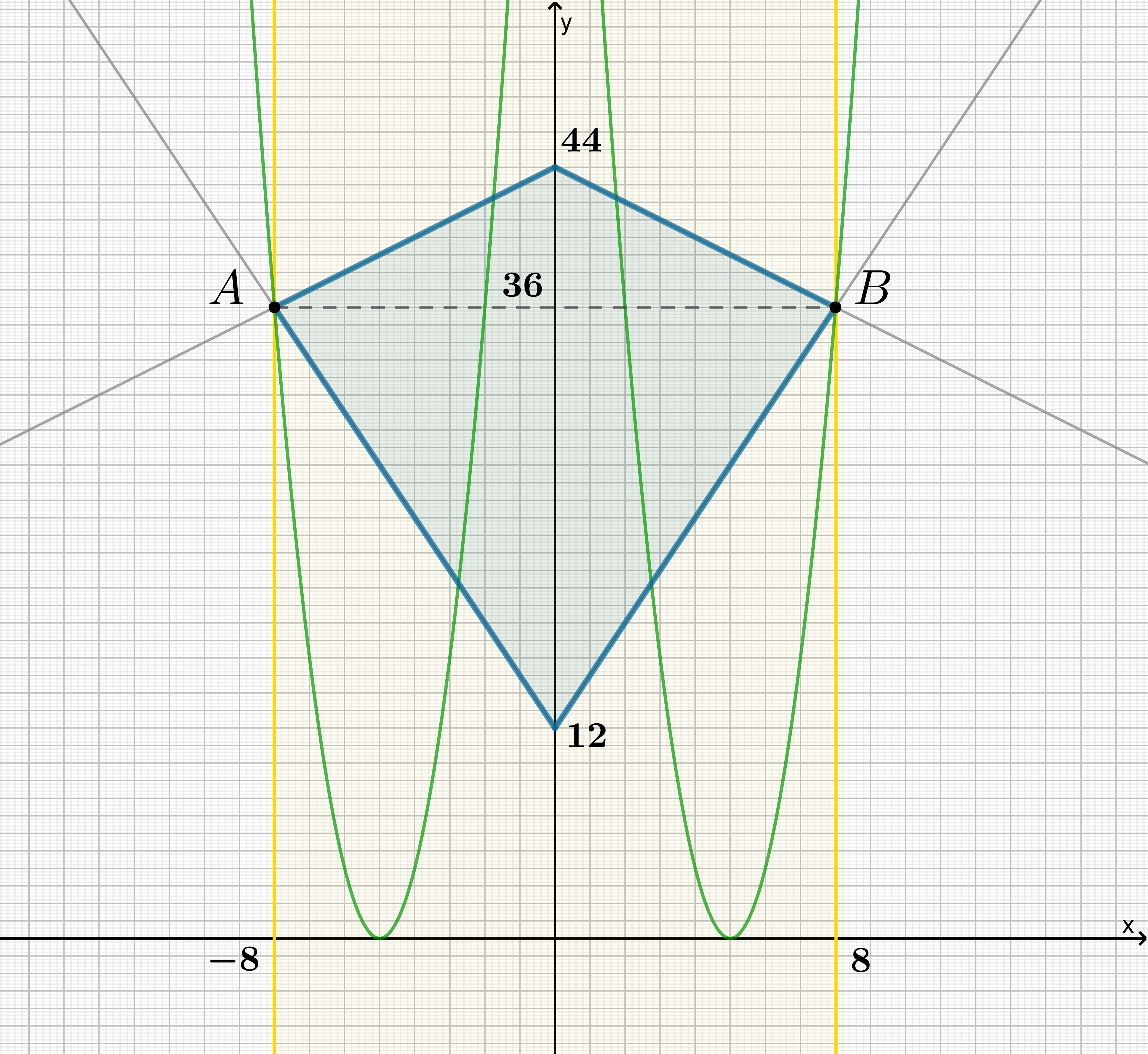
Так как вершина параболы находится в точке , то при изменении
от
до
парабола движется слева направо,
следовательно,
соответствует положению параболы, когда правая ветвь проходит через
, а не левая, а
— когда левая
ветвь, а не правая, проходит через
. Поэтому нам подходят
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
уравнений
имеет ровно два различных решения.
Преобразуем систему:
Решим систему графически. Найдем точки пересечения графиков функций
и
Следовательно, имеем две точки пересечения: и
Тогда нам
подойдут те значения параметра
при которых точки
и
будут
находиться в горизонтальной полосе шириной 3, задаваемой неравенством
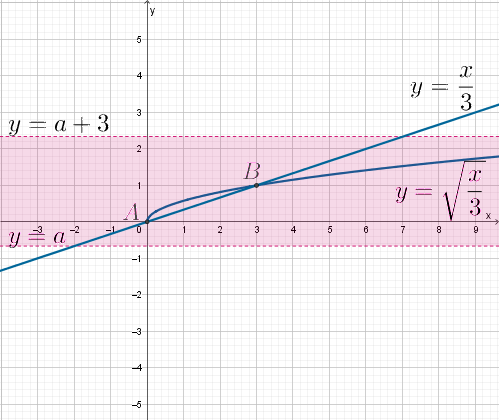
Так как полоса без границы, то необходимо, чтобы прямая находилась
ниже прямой, проходящей через точку
а прямая
находилась выше
прямой, проходящей через точку
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет единственное решение.
Преобразуем исходную систему:
Первое и третье уравнения системы задают параболы на плоскости. Второе неравенство системы задает часть плоскости,
лежащую строго ниже горизонтальной прямой Построим графики (первый при
второй при
).
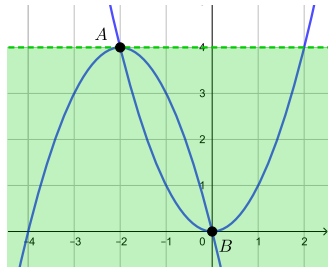
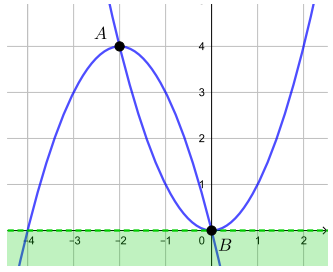
Параболы имеют две точки пересечения и
Чтобы система имела единственное решение,
должно быть
таковым, чтобы ровно одна из точек
и
лежала ниже прямой
- При
точки
и
лежат ниже прямой
то есть система имеет два решения, такие
нам не подходят.
- При
точка
лежит выше «разрешенной» области (другими словами, не удовлетворяет условию
), а точка
принадлежит «разрешенной» области, то есть система имеет ровно одно решение, такие
нам подходят.
- При
ни одна из точек не лежит в «разрешенной» области (другими словами, ни одна из точек не удовлетворяют условию
) и система не имеет ни одного решения, такие
нам не подходят.
Таким образом, нам подходят
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получено
множество значений | 3 |
| С
помощью верного рассуждения получены
все граничные точки искомого множества
значений | 2 |
| Верно получена хотя бы одна граничная
точка искомого множества значений | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |



