Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых система
имеет решения.
Преобразуем первое уравнение:
Оно задает окружность с центром в точке и радиусом
Найдем траекторию центра окружности:
Таким образом, первое уравнение исходной системы задает окружность с центром в произвольной точке прямой и
радиусом
Второе уравнение исходной системы — это прямая
Построим графики.
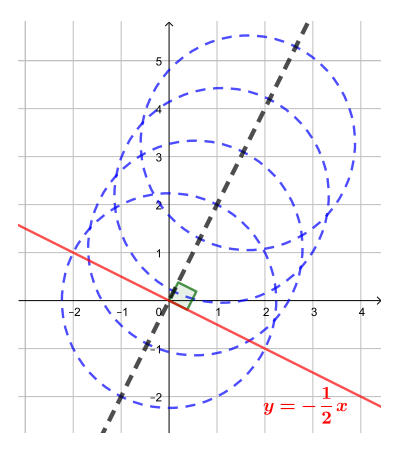
Нас интересуют значения при которых окружность имеет точки пересечения с прямой
значит, ключевыми
положениями на рисунке для нас будут касания окружности с этой прямой. Заметим, что прямая
и
прямая-траектория
перпендикулярны. Следовательно, окружность будет касаться прямой
только в том
случае, если ее центр находится на расстоянии, равном радиусу окружности, от точки пересечения прямых — начала координат.
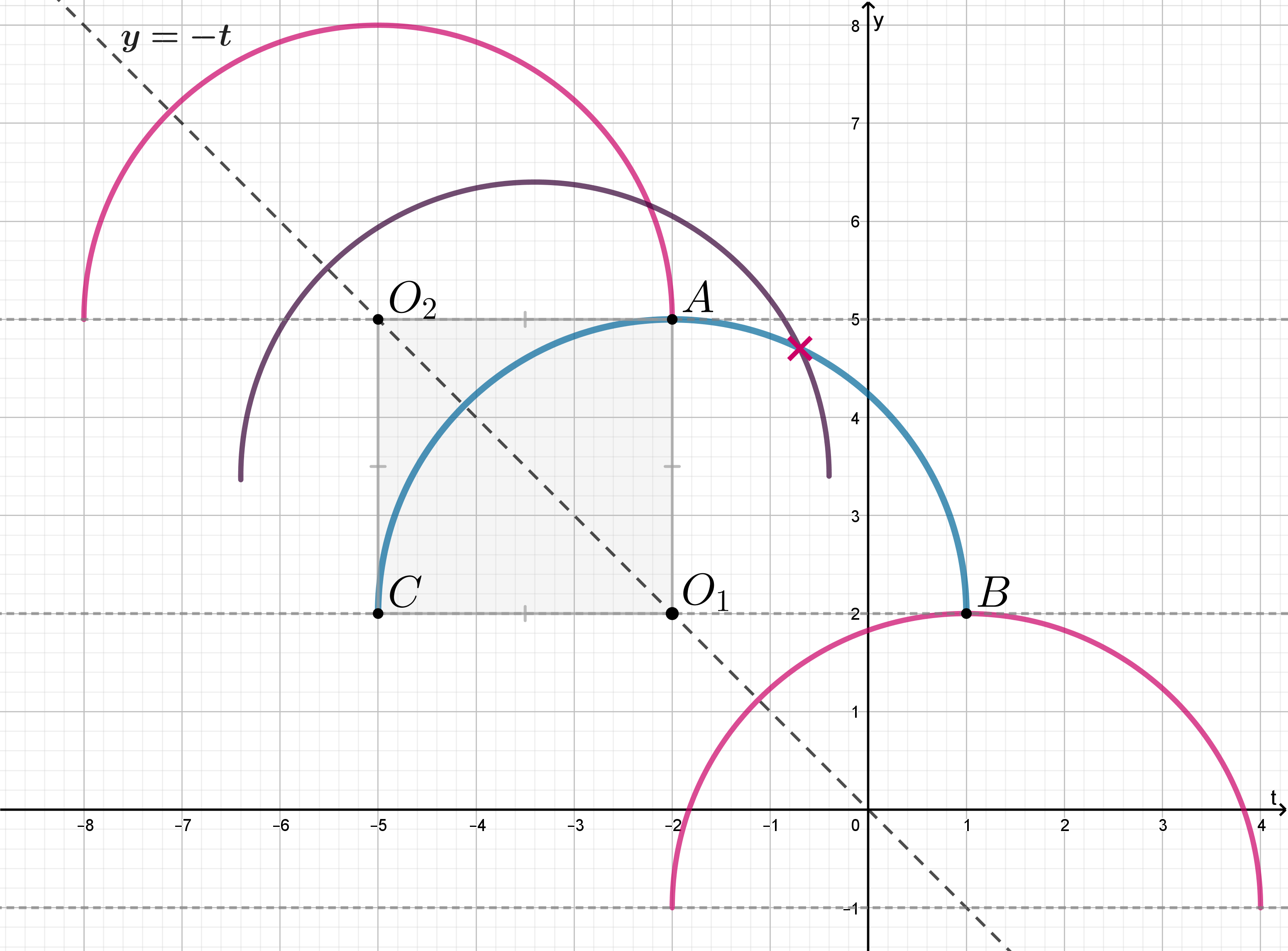
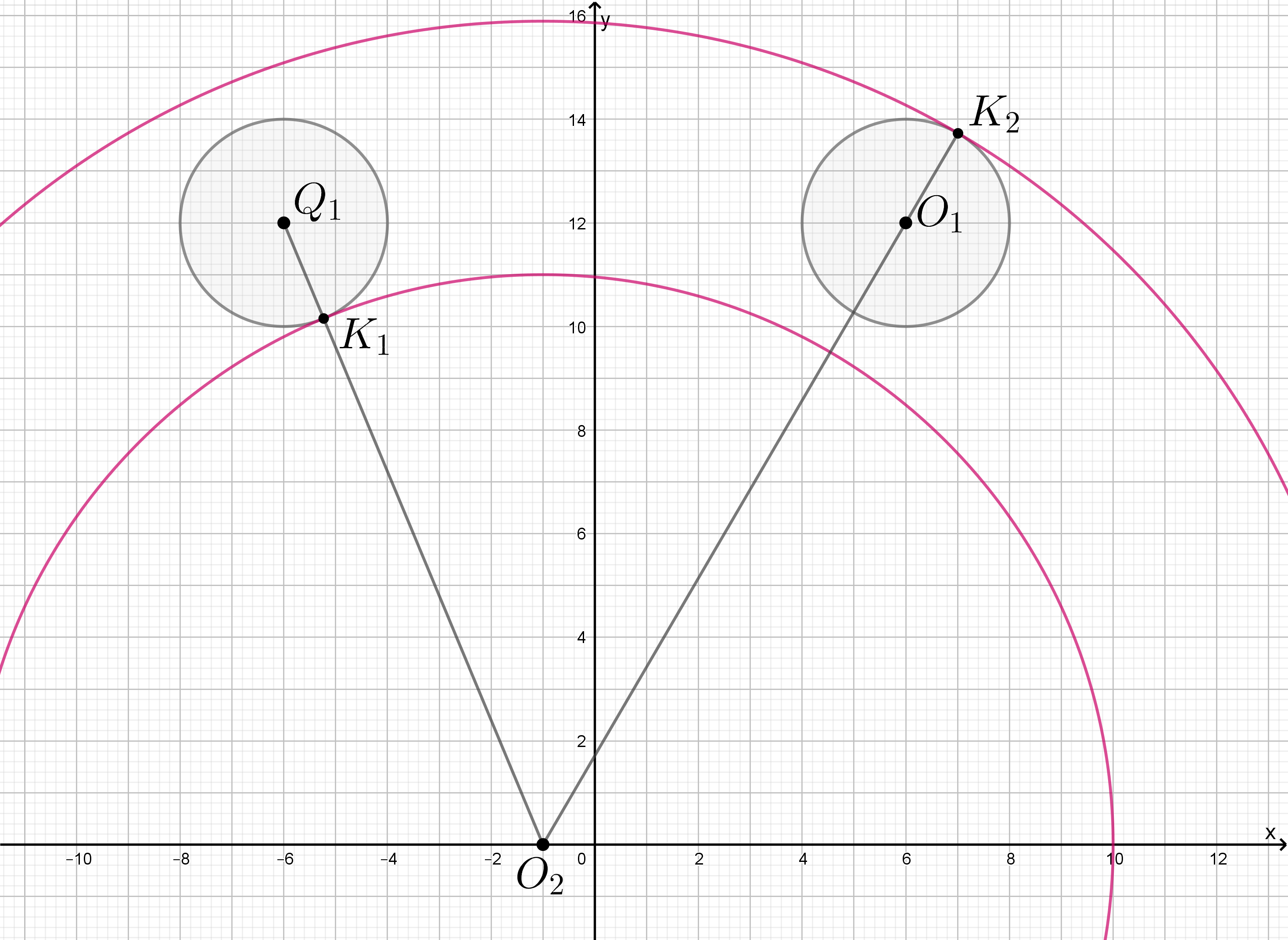
Изобразим случаи касания на картинке, начало координат обозначим через
центры окружностей в случаях касания — через
и
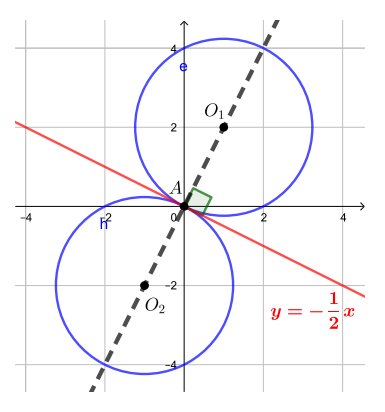
Мы поняли, что точки и
таковы, что
Очевидно также, что
и
Найдем
записав условие на расстояние между
и
Так как то получаем
Очевидно, что при любых
то есть когда центр принадлежит
отрезку
окружность будет иметь пересечения с прямой
а при любых
для которых
— не будет.
Получаем ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно найдены граничные
значения | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
При каких значениях параметра касаются графики, задаваемые уравнениями
Первому уравнению соответствует семейство окружностей с центрами на оси ординат, так как координаты центра и
радиусом, равным 2. Второе уравнение задает прямую. Построим графики.
![]()
Сначала рассмотрим случай, когда то есть центр окружности лежит в верхней полуплоскости. Чтобы окружность с
центром
и радиусом 2 касалась прямой, расстояние от центра до этой прямой должны быть равно 2. Выразим
через
расстояние от центра окружности до прямой, а затем приравняем его к 2, чтобы найти подходящие
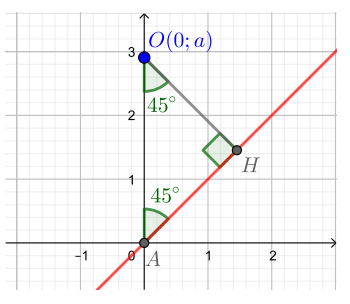
Опустим перпендикуляр на прямую
начало координат обозначим через
Мы знаем, что прямая
образует угол
с осью абсцисс, следовательно, угол
также равен
Тогда треугольник
— прямоугольный
равнобедренный с гипотенузой
значит, его катет равен
Приравняем эту величину к радиусу и найдем
Для отрицательного то есть когда центр окружности лежит в нижней полуплоскости, картинка будет симметричной, а
значит,
нам тоже подойдет. Тогда окончательно имеем:
![]()
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно рассмотрено одно из двух взаимных
расположений графиков функций, при
этом верно найдено хотя бы одно из
значений параметра | 2 |
| ИЛИ | |
| значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых система
имеет более двух решений.
Первое уравнение равносильно:
Первая система задает в области под прямой часть окружности с центром в
и радиусом
Вторая система задает в области над прямой
часть окружности с центром в
и тем же радлиусом. Заметим,
что эти окружности пересекаются, и пересекаются на прямой
Назовем множество, являющееся объединением этих
двух частей окружностей
Тогда требуется найти такие положения прямой при которых она с множеством
имеет более двух точек
пересечения.
Заметим, что угловые коэффициенты прямых и
в произведении дают
следовательно, эти
прямые взаимно перпендикулярны, таким образом, прямая
является осью симметрии для
и для прямой
следовательно, если
касается одной окружности из
то она касается и второй окружности из
Найдем граничные положения этой прямой:
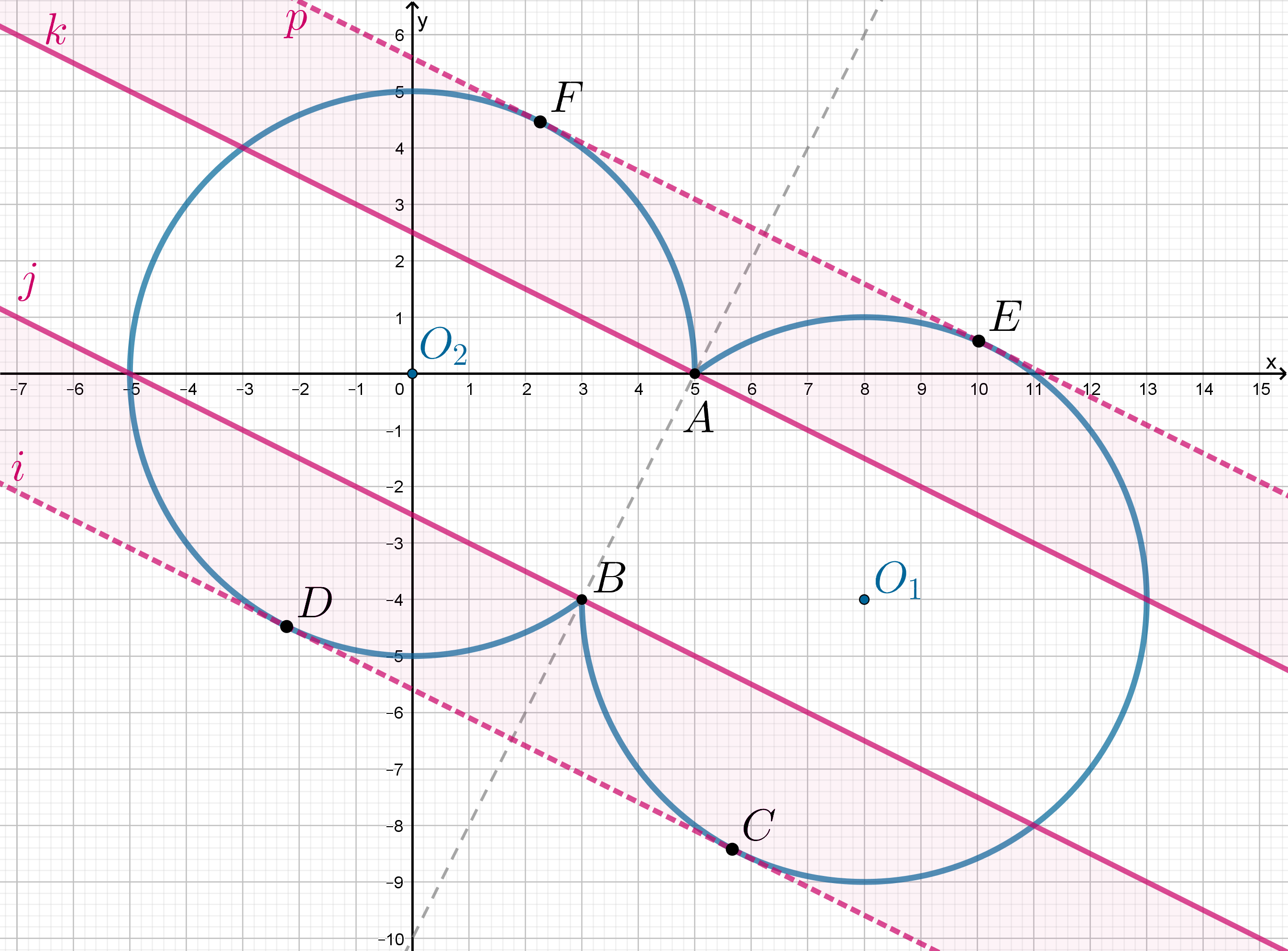
Следовательно, находясь в розовой области, прямая имеет с
более двух общих точек.
-
-
касается окружностей в точках
и
Найдем
задавая это положение следующим образом: расстояние от центра второй окружности до прямой равно радиусу окружности
Нам подходит меньшее
(когда прямая касается окружности снизу), то есть
-
-
аналогично предыдущему пункту
Нам подходит большее
(когда прямая касается окружности сверху), то есть
-
-
Найдем координаты точек
и
как точек пересечения
и окружности
Следовательно, из
следует
-
:
-
аналогично предыдущему пункту
Следовательно,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточно обоснованно построение или недостаточно обоснован какой-то момент при исследовании | 3 |
| Верно найдены граничное значение параметра, но есть ошибка в исследовании количества решений | 2 |
| ИЛИ | |
| допущена вычислительная ошибка | |
| Сведено к исследованию графически или аналитически и выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Перепишем систему в виде
Так как замена линейная, то в новых координатах
и
система также должна иметь единственное
решение.
В системе координат первое и третье равенства, учитывая второе и третье неравенства, задают верхние полуокружности
с центрами в точках
и
соответственно и одинаковыми радиусами
. Следовательно, нам
необходимо, чтобы эти полуокружности имели одну точку пересечения.
Заметим, что первая полуокружность фиксирована, а вторая при изменении от
до
движется
сверху вниз по прямой
. Также заметим, что центр первой окружности тоже лежит на прямой
.
Следовательно, положения второй полуокружности, при которых она имеет одну точку пересечения с первой,
такие:
Заметим, что когда правый конец одной из полуокружностей лежит на другой полуокружности, то для другой
полуокружности эта точка — наивысшая (то есть точка с максимальной ординатой) точка этой полуокружности. Речь
идет о точках и
.
Действительно, — ромб, так как
, диагональ
которого со стороной
образует угол в
, следовательно, это квадрат, следовательно,
. Аналогично для точки
.
Тогда нам подходят все положения второй полуокружности между теми, когда она проходит через точки
и
(включая эти положения), исключая положение, когда она совпадает с первой полуокружностью. Так
как мы доказали, что
— квадрат, то ордината
для “положения
” равна
, а для “положения
” равна
(на
единицы больше/меньше ординаты
). Следовательно,
, откуда
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С
помощью верного рассуждения получены
все значения | 3 |
| С помощью верного рассуждения
получены не все значения | 2 |
| Задача верно сведена к исследованию взаимного расположения графика функции и прямой (аналитически или графически) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых система уравнений
имеет нечетное число различных решений.
По теореме Виета, если рассматривать первое уравнение как квадратное относительно , получаем
Равенство задает верхнюю полуокружность от окружности
(которая, заметим, целиком лежит в правой
полуплоскости), тогда равенство
задает две верхние полуокружности
и
. Таким образом,
система равносильна:
Изобразим график совокупности в области, задающейся неравенством и определим те положения прямой
, при
которых она с этим графиком (голубой) имеет нечетное число точек пересечения.
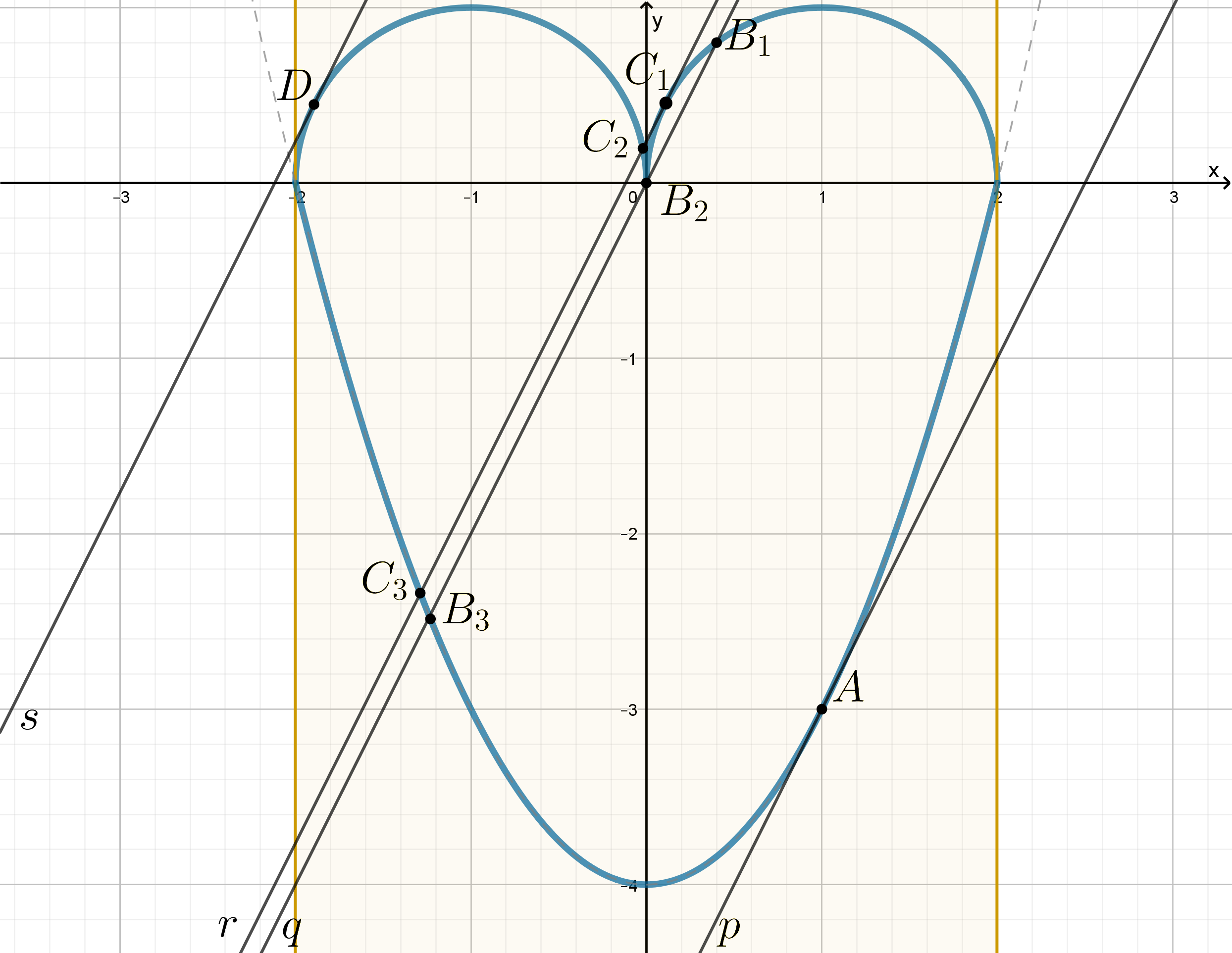
-
:
-
прямая касается параболы в точке
;
-
:
-
прямая проходит через “стык” двух полуокружностей — через начало координат
(также пересекает правую полуокружность в точке
и параболу в точке
);
-
:
-
прямая касается правой полуокружности в точке
(также пересекает левую полуокружность в точке
и параболу в точке
);
-
:
-
прямая касается левой полуокружности в точке
Найдем значения параметра, соответствующие этим положениям прямой.
-
:
-
Ищем касание прямой и параболы (через равенство функций и производных в точке касания):
-
:
-
прямая проходит через
, если
-
:
-
прямая касается окружности, если расстояние от центра окружности до прямой равно радиусу окружности:
Нашему положению соответствует большее
(так как меньшее соответствует более низкому положению прямой, когда она касается отсутствующей нижней правой полуокружности). Следовательно,
-
:
-
аналогично предыдущему пункту
Нашему положению соответствует большее
(так как меньшее соответствует более низкому положению прямой, когда она касается отсутствующей нижней левой полуокружности). Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет одно решение.
Система равносильна
Так как замена линейная, то в новых переменных
и
система также должна иметь единственное решение.
Таким образом, в системе координат первое уравнение задает окружность с центром в точке
и радиусом
,
движущуюся по прямой
, а второе уравнение задает уголок, строящийся в следующей последовательности:
Одно решение система имеет в том случае, когда окружность касается уголка.
Так как график симметричен относительно оси ординат, то в Положении 1 будем рассмативать касание окружности и
уголка в точке
и в точке
(причем этим касаниям соответствуют противоположные значения параметра), а в Положении 2 — касание
в точке
и в точке
(чему также соответствуют противоположные значения параметра).
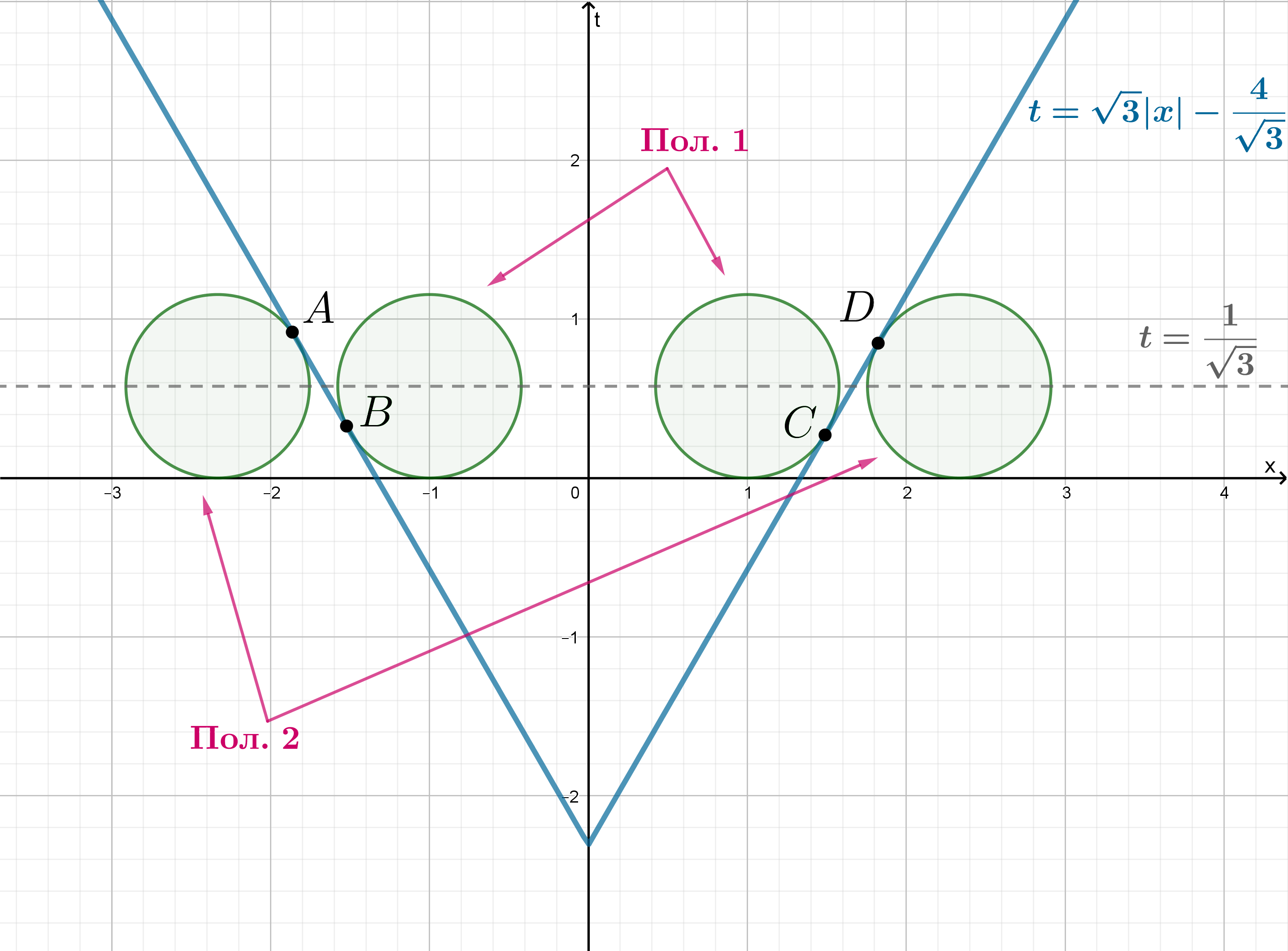
Рассмотрим касание в точке и в точке
. Тогда расстояние от центра окружности до левой ветви уголка
равно
радиусу окружности, следовательно:
Тогда касанию в точке соответствует
, а касанию в точке
соответствует
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все , при которых система
имеет ровно два различных решения.
Второе уравнение системы равносильно
Следовательно, оно задает окружность с центром
и радиусом
. Значит, при изменении
от
до
окружность
движется снизу вверх по прямой
. Первое уравнение задает “птичку”, которая строится в следующей
последовательности:
Рассмотрим следующие положения:
- 1.
- Верхняя часть окружности проходит через точку
Пусть этому положению соответствует
.
- 2.
- Нижняя часть окружности проходит через точку
Пусть этому положению соответствует
.
- 3.
- Окружность вписана в угол
.
Заметим, что диагональ клетки равна
, следовательно, половина диагонали клетки равна
. Также заметим, что две диагонали клетки взаимно перпендикулярны, следовательно, если окружность касается
, то она также касается и отрезка
, причем в серединах обоих отрезков — в точках
и
соответственно (так как слетка представляет собой квадрат).
Пусть этому положению соответствует
.
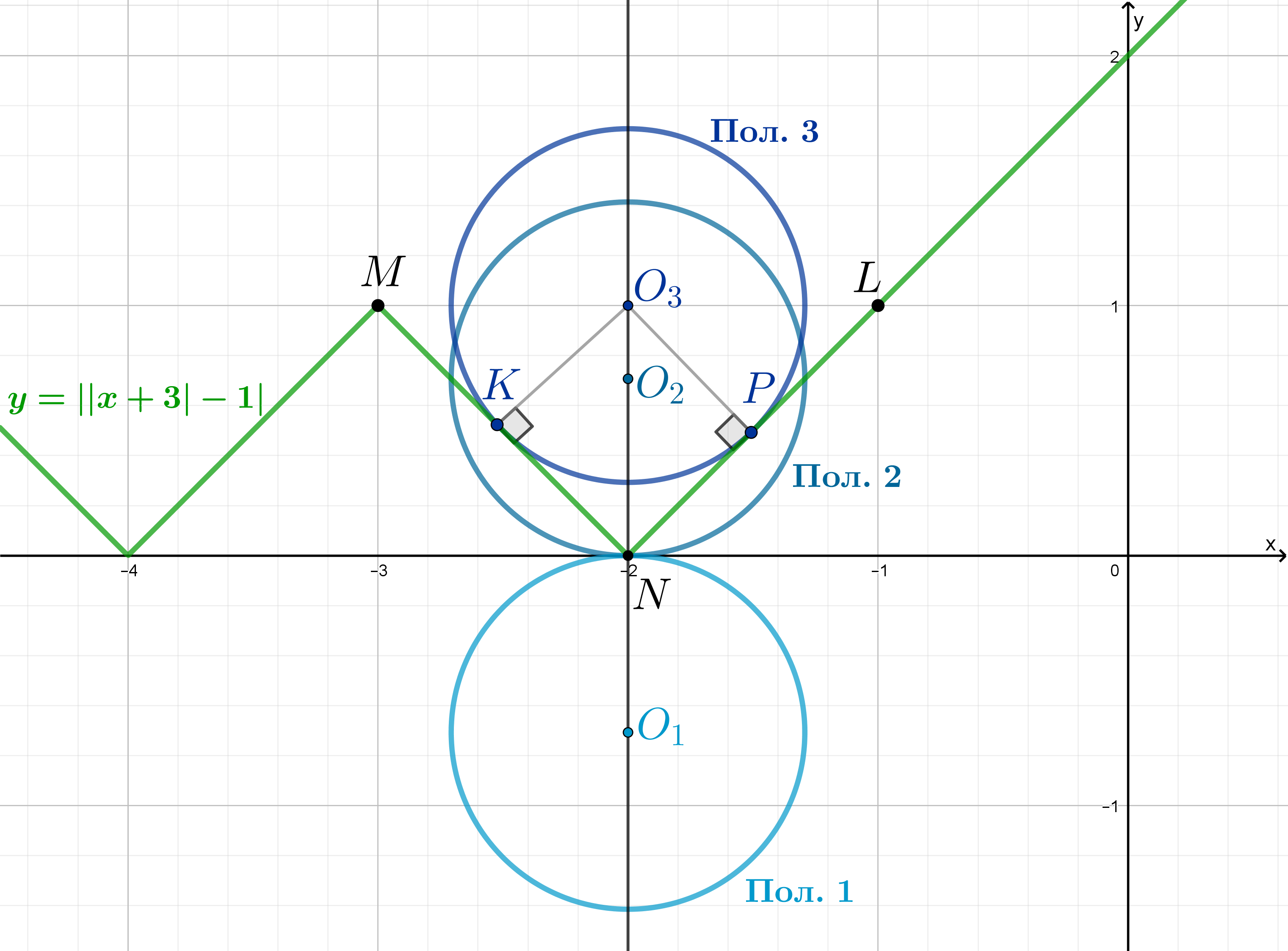
Заметим, что при изменении от
до
окружность последовательно проходит через положения 1, 2 и 3 (в указанном
порядке). Тогда нам подходят
Найдем нужные значения параметра.
-
:
-
лежит на окружности:
Этому положению соответствует
, так как ордината центра окружности отрицательная.
-
:
-
лежит на окружности:
Этому положению соответствует
, так как ордината центра окружности положительная.
-
:
-
центр окружности находится в узле клетки (вершина квадрата), следовательно,
.
Таким образом,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет единственное решение.
Первое уравнение системы задает окружность с центром в точке
и радиусом
при
и точку
при
; второе уравнение задает окружность
с центром в точке
и радиусом
при
и точку
при
.
Окружность, вырождающуюся в точку, называют вырожденной.
Две окружности (в том числе и вырожденные) имеют одну точку пересечения, если они касаются (в случае точки и окружности это
значит, что точка лежит на окружности, а в случае двух точек — что они совпадают). При касании внешним образом
сумма радиусов равна расстоянию между центрами окружностей:
; при касании
внутренним образом модуль разности радиусов равен расстоянию между центрами окружностей:
.
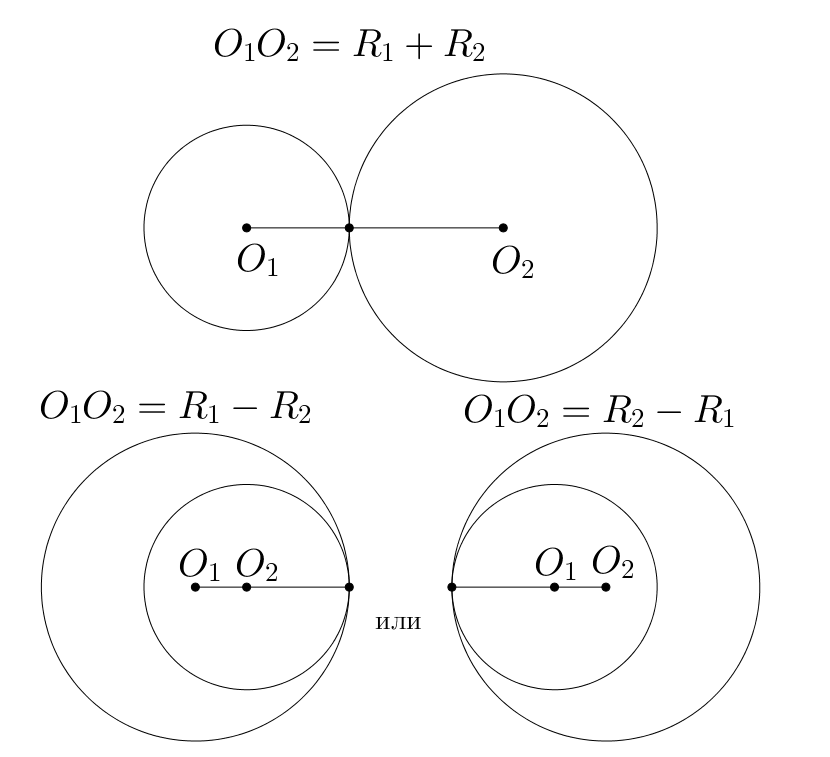
Следовательно,
Таким образом,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Первое уравнение системы задает окружность с центром в точке
и радиусом
, а второе уравнение задает
окружность
с центром в точке
и радиусом
.
Две окружности имеют одну точку пересечения, если они касаются. При касании внешним образом сумма радиусов равна расстоянию
между центрами окружностей: ; при касании внутренним образом модуль разности радиусов равен расстоянию между
центрами окружностей:
.
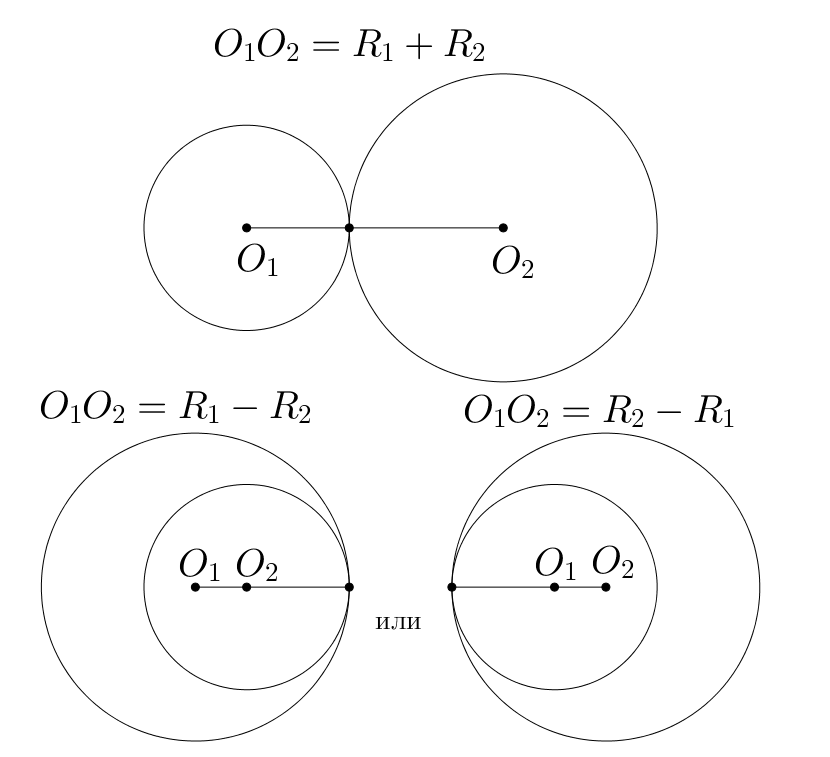
Следовательно,
Таким образом,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет единственное решение.
Преобразуем первое равенство:
Тогда первое уравнение системы задает окружность с центром в точке
и радиусом
, а второе уравнение задает
окружность
с центром в точке
и радиусом
при
и точку
при
.
В случае система имеет единственное решение, если
, что проверяется подстановкой координат точки в уравнение
окружности:
Получили неверное равенство, следовательно, , значит,
нам не подходит.
Пусть . Тогда две окружности имеют одну точку пересечения, если они касаются. При касании внешним образом сумма радиусов
равна расстоянию между центрами окружностей:
; при касании внутренним образом модуль разности радиусов равен
расстоянию между центрами окружностей:
.
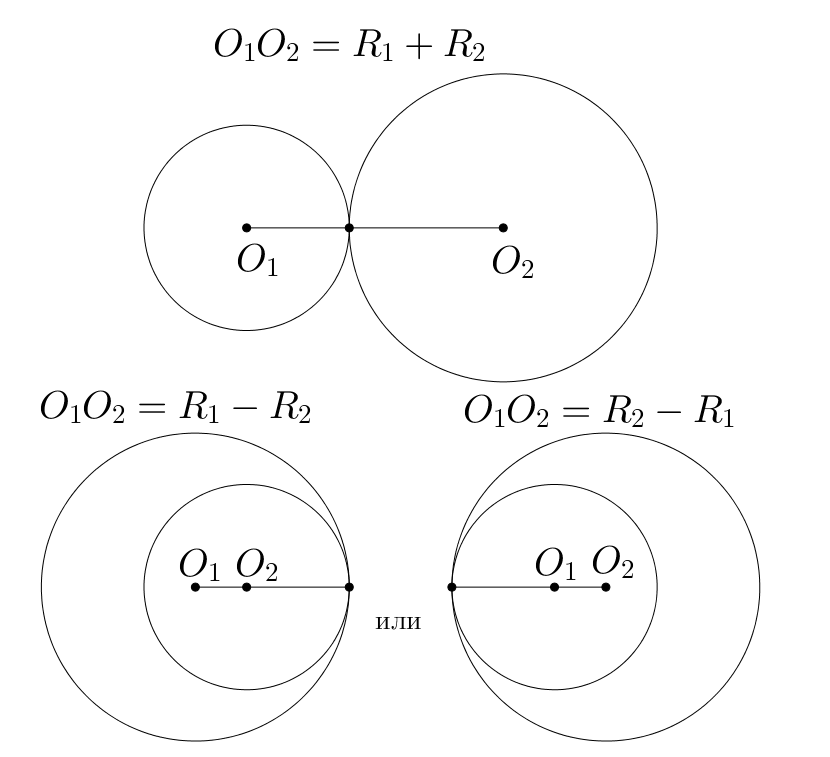
Следовательно,
Таким образом,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет три различных решения.
Первое уравнение задает окружность с центром и радиусом
Второе уравнение задает уголок, вершина которого движется
по прямой
(заметим, что эта прямая касается окружности). Причем при изменении
от
до
уголок движется слева
направо. Три точки будет в следующих позициях:
- касание в
левой ветви уголка и окружности;
- вершина уголка находится в точке касания окружности и
;
- касание в
правой ветви уголка и окружности.
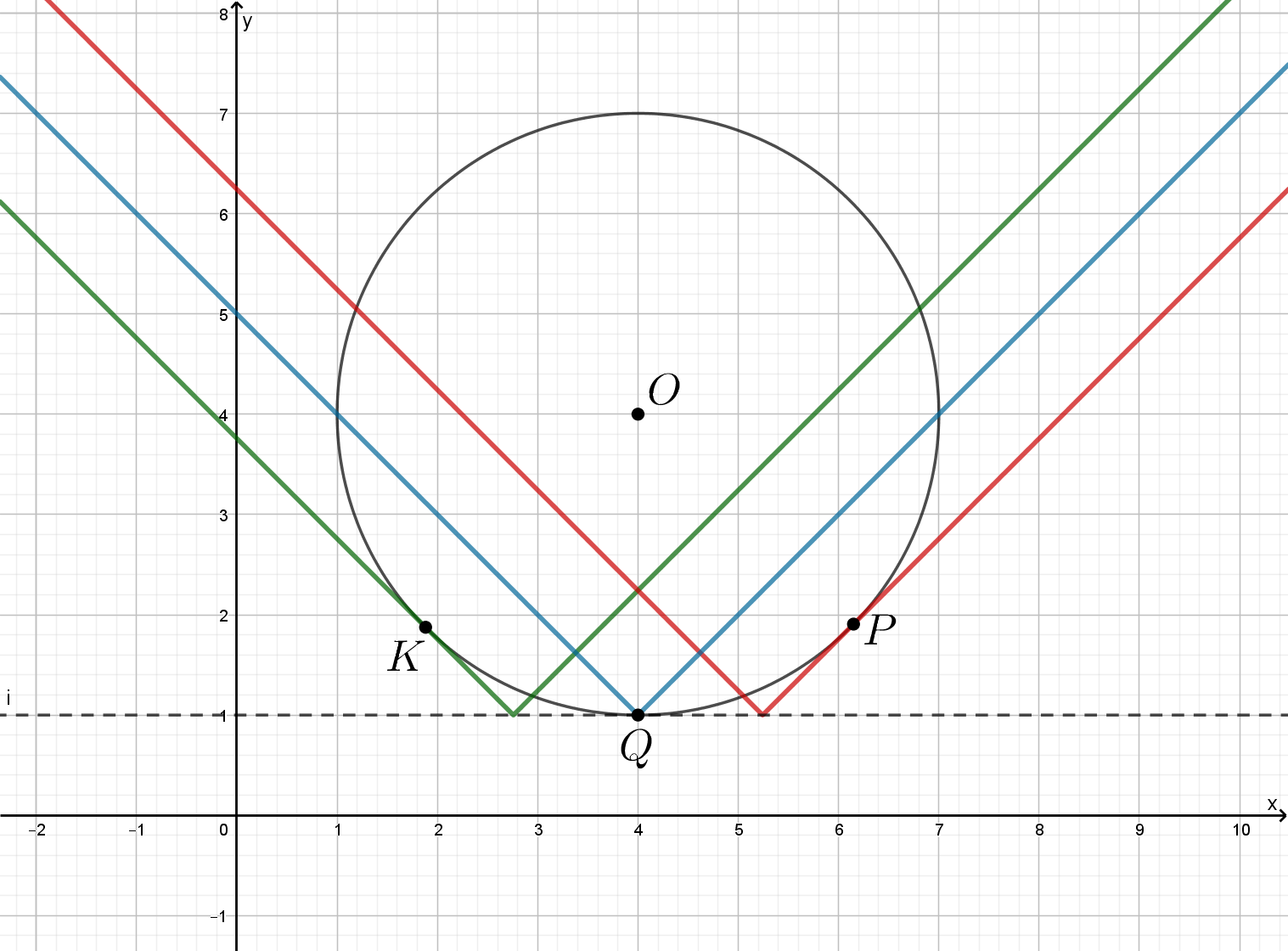
Если прямая касается окружности, то это условие можно задать с помощью формулы расстояния от точки до прямой: в случае
окружности это расстояние должно быть равно радиусу окружности. Для центра окружности радиусом
и прямой
,
задаваемой
, это уравнение выглядит так:
Следовательно, так как , то есть
,
, то есть
,
получаем
Для точки нужно выбрать меньшее значение параметра (так как существует еще одно положение, когда левая ветвь касается
окружности, и оно правее нужного нам положения), для точки
— большее значение параметра (по аналогичным причинам). Вершина
уголка в точке
, если
.
Следовательно, .
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет единственное решение.
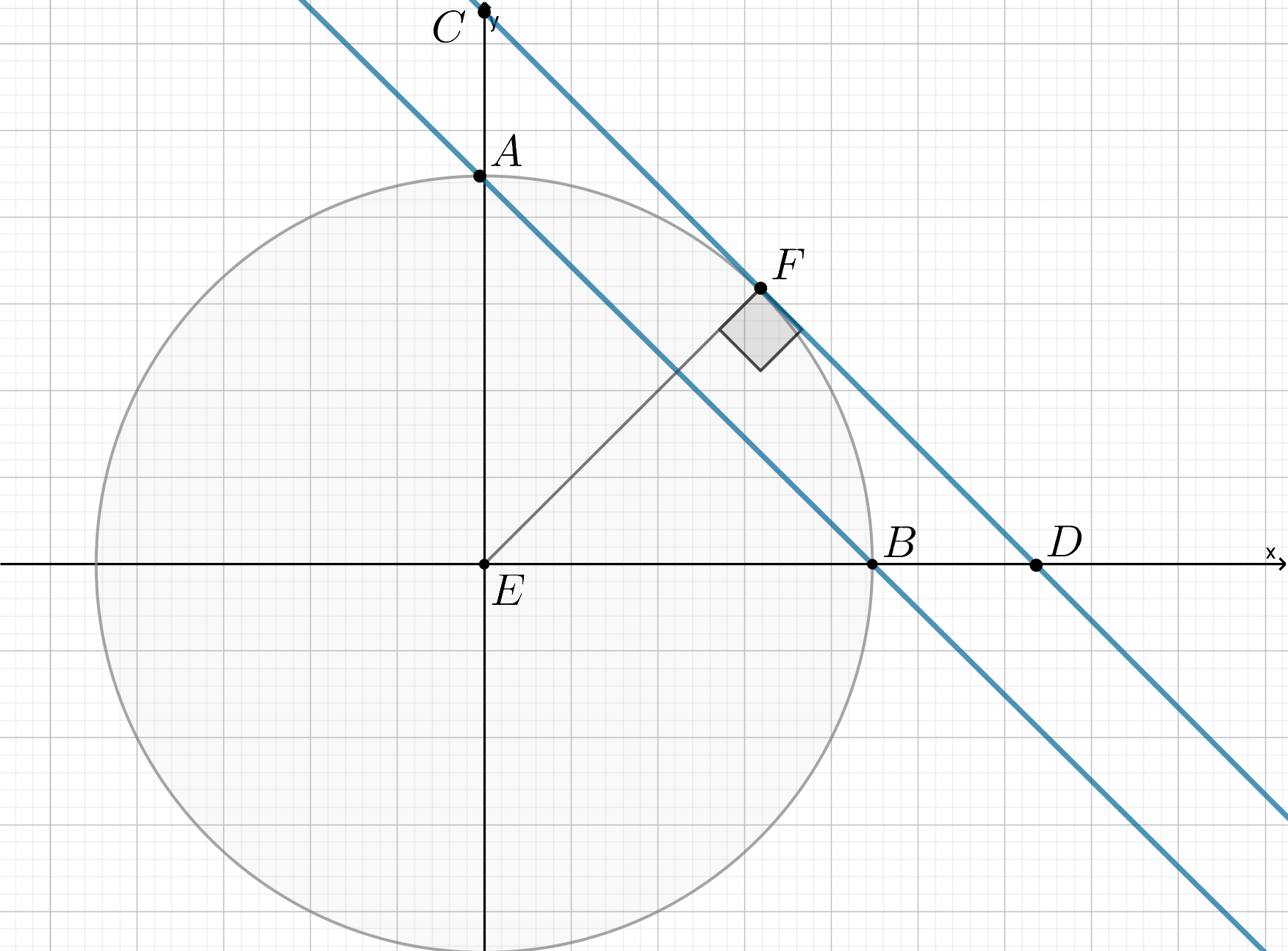
Первое уравнение представляет собой две части окружностей: одна с центром в точке и радиусом
, вторая — с центром
и тем же радиусом. Заметим, что расстояния от центра окружностей до оси ординат меньше радиуса, следовательно, обе
окружности берутся целиком.
Второе уравнение — окружность с центром и радиусом
(назовем ее
).
Две окружности имеют одну общую точку, если они касаются внешним или внутренним образом. Следовательно, должна касаться
одним из двух способов с одной окружностью и вовсе не иметь общих точек с другой. Заметим, что расстояние от центра
до первой
окружности меньше, чем до центра второй, следовательно, первое касание будет внешним с первом окружностью, затем внешнее со второй,
затем внутреннее с первой, затем внутреннее со второй. Следовательно, нам подходят только первый и четвертый случай:
Тогда
Ошибка.
Попробуйте повторить позже
Найдите , при которых система
имеет ровно четыре решения.
Пусть , тогда
не дает решений
,
дает одно решение
,
дает два различных решения
Система примет
вид
Первое уравнение задает либо точку, либо окружность. Случай с точкой не подходит, потому как тогда смистема максимум может иметь одно решение.
Тогда первое уравнение задает окружность с радиусом , а второе — прямую. Окружность с прямой могут иметь 0, 1 или 2 точки
пересечения. Следовательно, чтобы после обратной замены мы получили четыре решения, необходимо, чтобы прямая имела с окружностью
две точки пересечения, абсциссы которых положительны.
Нам подходят все прямые между и
.
Выше прямой
;
ниже прямой
.
Следовательно,
Получаем
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Перепишем уравнение в виде где
Графиком является верхняя полуокружность окружности
график
представляет собой
пучок прямых, проходящих через точку
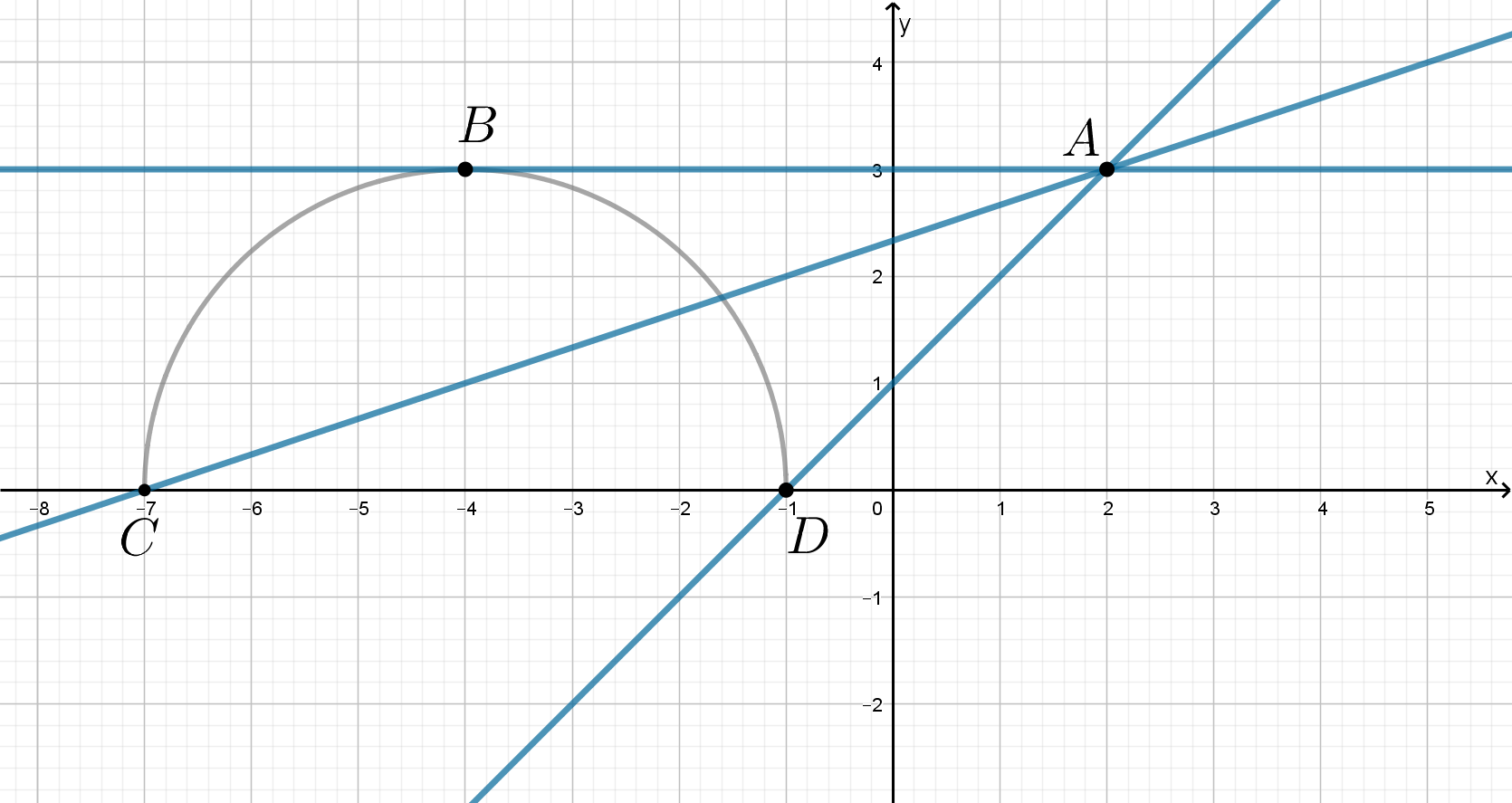
Положения прямой которые нам подходят:
когда прямая проходит через точку
когда прямая находится между прямыми, проходящими через точки и
включая положение
Найдем значения параметра, соответствующие прохождению прямых пучка через точки
Тогда исходное уравнение имеет единственное решение при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Верно рассмотрено два из трех взаимных
расположений графиков функций, при
этом верно найдено хотя бы одно из
значений параметра | 2 |
| ИЛИ | |
| значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите , при которых система
имеет ровно два различных решения.
Рассмотрим вторую скобку:
Следовательно, система равносильна:
Найдем те , при которых горизонтальная прямая
имеет две точки пересечения со множеством
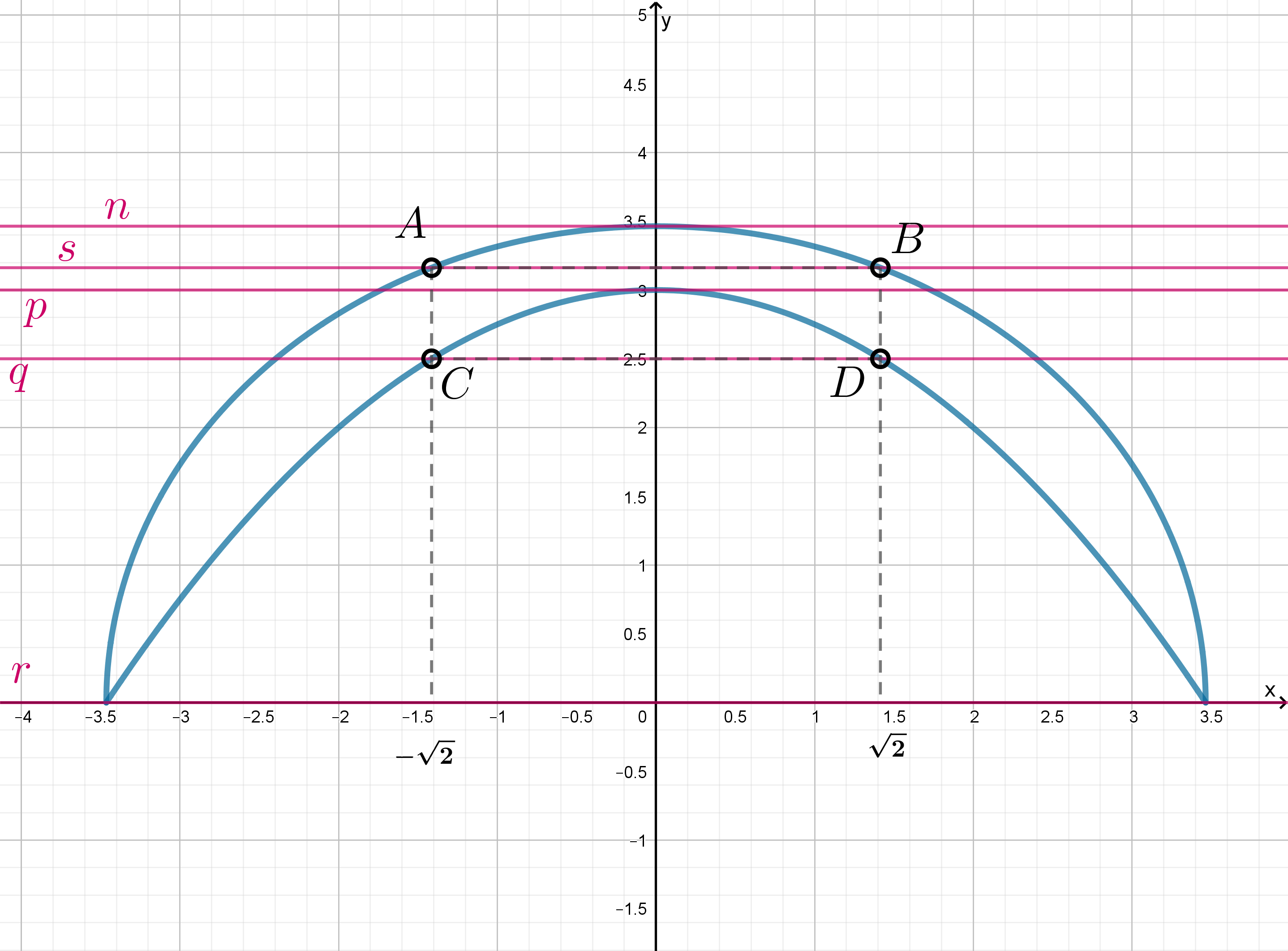
Заметим, что в силу симметрии полуокружности и параболы относительно оси ординаты точек
и
одинаковы, а также
одинаковы ординаты точек
и
. Прямая
будет иметь с голубым графиком две точки пересечения, находясь в положении
, в положении
и между положениями
и
, исключая положение
.
Ищем ординату точек и
.
Ищем ординату точек и
;
;
;
;
.
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения при каждом из которых система уравнений
имеет ровно два различных решения.
Источник:
Рассмотрим второе уравнение системы:
Рассмотрим первое уравнение системы:
Если сделать замену
то система равносильна
В системе координат первое уравнение задает две прямые, проходящие
через точку
и симметричные относительно оси ординат. Второе уравнение
задает окружность с центром в точке
и радиусом
проходящую
через точку
Необходимо, чтобы две прямые
и
имели две
точки пересечения с той частью окружности, что находится в области
Изобразим графики:
Пусть Тогда если
является решением задачи, то
также
является решением задачи.
Заметим, что при любом прямые
и
пересекаются с
окружностью в начале координат, то есть одно решение система имеет
всегда.
Рассмотрим позицию (1): прямая касается окружности в точке
Тогда система имеет одно решение. Но все прямые, находящиеся между осью
ординат и прямой
имеют две точки пересечения с окружностью в
области
А прямая
в свою очередь, не имеет общих точек с
этой частью окружности (кроме повторяющейся точки
). Следовательно,
если
— параметр, соответствующий положению (1), то нам подходят все
Рассмотрим положение (2), когда прямая проходит через точку
Так как эта точка выколота, то обе прямые в совокупности имеют две общие точки
с частью окружности, значит, все положения прямых между положениями (1) и
(2), включая (2), нам подходят. То есть если
— параметр, соответствующий
положению (2), то нам подходят
Положение (3): прямые и
совпадают и дают прямую
которая имеет с частью окружности две общие точки. Следовательно, это
положение нам тоже подходит. Сразу можно заметить, что оно получается при
Найдем система должна иметь единственное решение
Тогда второе уравнение системы имеет единственное решение откуда
получаем
Найдем
Следовательно,
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет ровно два различных решения.
Перепишем систему в виде
Первое уравнение задает окружность с центром в точке и радиусом
Второе уравнение задает прямую. Пусть окружность с прямой
пересекаются в точках
и
Тогда нам необходимо, чтобы прямая
имела ровно две общие точки со множеством
где
—
объединение прямой
и верхней дуги
окружности.

Нам подходят положения 1 и 4, а также все положения между 2 и 3, включительно 2 и 3.
Найдем и
Они соответствуют положениям 1 и 4 соответственно, когда
прямая
касается окружности. Тогда расстояние от точки
до этой
прямой равно радиусу окружности. Прямую для использования формулы
расстояния от точки до прямой следует переписать в виде
Следовательно,
Найдем и
соответствующие положениям 2 и 3 соответственно, когда
прямая
проходит через точки
и
Найдем для начала
координаты этих точек. Для этого решим систему:
Следовательно,
Следовательно, для положения 2 имеем
Для положения 3 имеем
Таким образом, ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения
получены верные значения параметра | 3 |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения | 2 |
| ИЛИ | |
| верно рассмотрены два положения из четырех | |
| В случае аналитического решения: задача верно сведена к набору решенных уравнений и неравенств с учетом требуемых ограничений | 1 |
| ИЛИ | |
| в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система уравнений
|
|
имеет единственное решение.
Рассмотрим систему внимательнее и преобразуем её условия:
|
|
|
|
|
|
|
|
Получили полуокружность и пучок прямых, проходящих через точку .
Перейдём на координатную плоскость
:
1 случай:
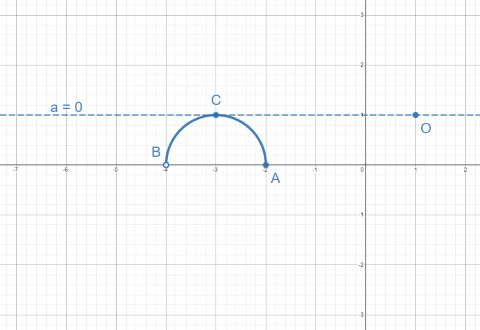
При прямая
становится параллельной оси абсцисс и
проходит ровно через одну точку
полуокружности. Иными словами,
касается полуокружности – такой случай нам подходит и
– часть
ответа.
2 случай:
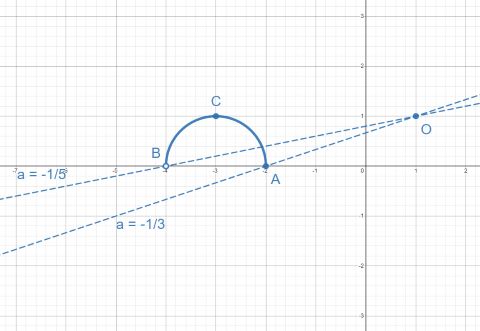
Когда прямая
пересекает полуокружность ровно в
одной точке. Иными словами, мы берём в ответ все прямые, лежащие между
прямыми
и
, включая
и исключая
.
пересекает
полуокружность уже в двух точках.
Вычисления ключевых значений параметра:
Прямая (проходит через точку
):
Прямая (проходит через точку
):
Прямая (проходит через точку
):
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены все верные значения параметра, но решение недостаточно обосновано | 3 |
| ИЛИ | |
| в ответ включена точка | |
| ИЛИ | |
| потеряна точка | |
| ИЛИ | |
| потеряна точка | |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения | 2 |
| ИЛИ | |
| полученный
ответ отличается от правильного
включением/исключением двух или
трёх точек из набора | |
| В случае аналитического решения
найдено значение | 1 |
| ИЛИ | |
| в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Будем решать задачу графически. Графиком уравнения является уголок,
получаемый из уголка (вершина которого находится в точке
)
сдвигом на
единиц вправо и на
единиц вниз. Следовательно, вершина
уголка
— это точка с координатами
и
Тогда зависимость между этими координатами следующая:
причем
заметим, что
Следовательно, правая ветвь параболы
(то есть
часть параболы при
) — траектория, по которой движется вершина уголка
Графиком неравенства является круг (то есть окружность с внутренностью) с
центром в точке радиуса
Система имеет единственное решение, когда уголок и круг имеют ровно
одну общую точку, то есть одна из ветвей уголка касается окружности
а вторая не имеет с окружностью общих точек.
Изобразим графики.
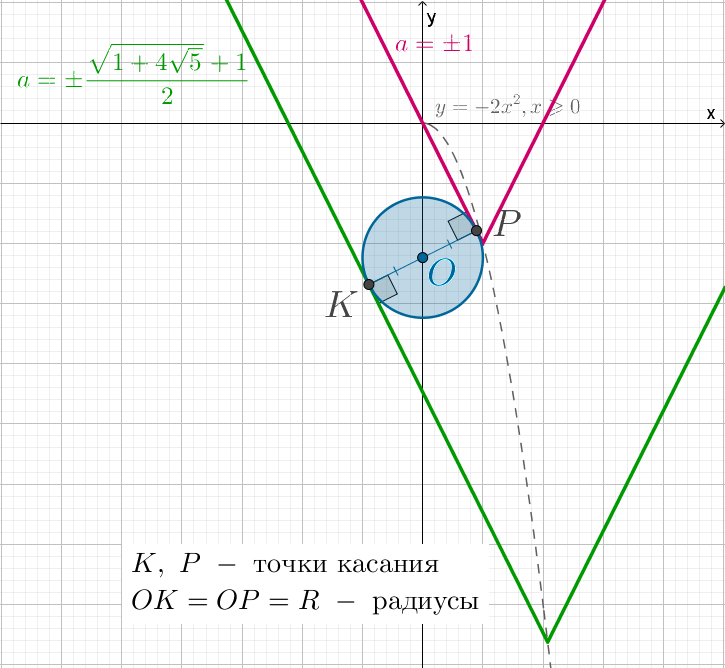
Заметим, что только левая ветвь (назовем ее лучом ) уголка может касаться
окружности. Ветвь
задается уравнением
или же
Запишем условие касания луча
и окружности
через формулу расстояния от точки до прямой: если прямая
задана уравнением
то расстояние от точки
до нее вычисляется по
формуле
Заметим, что при использовании этого способа найденные требуют
проверки, так как это условие задает касание прямой и окружности, а не луча и
окружности.
В случае касания левой ветви и окружности расстояние от центра
окружности до
должно быть равно радиусу окружности:
Заметим, что не подходит, так как в этом случае точка касания
находится не на луче
(задаваемом уравнением
), а на его
продолжении за вершину уголка, то есть на луче
при
а эти точки
не принадлежат уголку
что видно из рисунка:
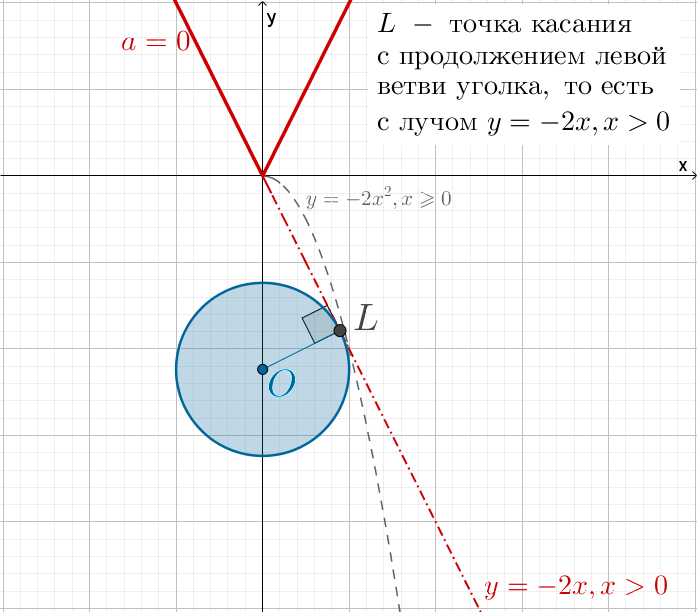
Следовательно, ответ:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет единственное решение.
Будем решать задачу графически. Графиком первого уравнения является уголок,
получаемый из графика функции (вершина которого находится в точке
) сдвигом на
единиц вправо, если
и влево, если
а затем
сдвигом на
единиц вверх. Следовательно, координаты вершины уголка
— это
Тогда между этими координатами
следующая зависимость:
Это значит, что парабола
является
траекторией движения вершины уголка.
Графиком второго уравнения является окружность с центром в точке
радиуса
Система имеет единственное решение, если ровно одна из ветвей уголка касается окружности, а вторая ветвь не имеет с окружностью общих точек.
Заметим, что окружность и парабола симметричны относительно оси ординат,
следовательно, если и вершина уголка находится в первой четверти,
то если левая ветвь уголка касается окружности при
тогда при
(когда вершина уголка находится во второй четверти) правая
ветвь касается окружности. Значит, достаточно рассмотреть только случай
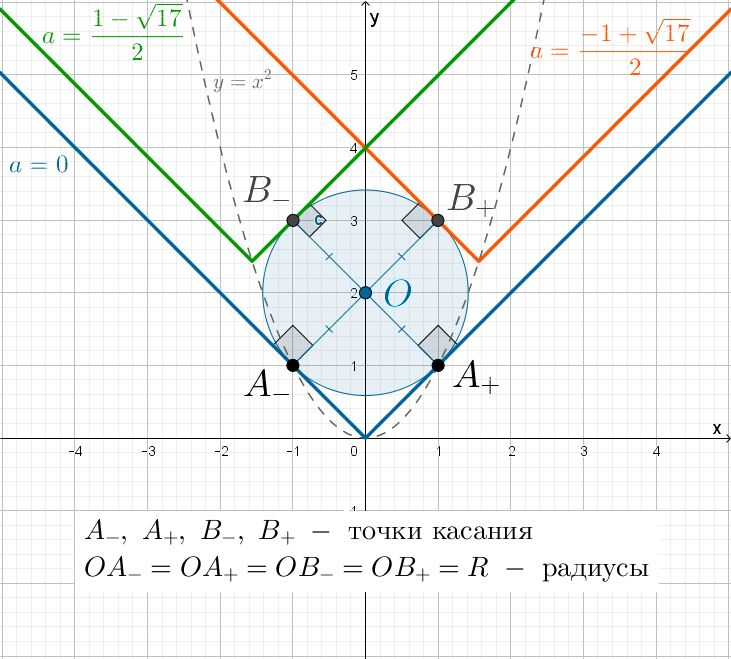
Пусть
Левая ветвь (назовем ее ) уголка задается уравнением
или
Запишем условие касания луча
и окружности через
формулу расстояния от точки до прямой: если прямая
задана уравнением
то расстояние от точки
до нее вычисляется по
формуле
Заметим, что при использовании этого способа найденные требуют
проверки, так как это условие задает касание прямой и окружности, а не луча и
окружности.
В случае касания левой ветви и окружности расстояние от центра
окружности до
должно быть равно радиусу окружности:
Так как мы рассматриваем случай то нам подходят лишь
Но при
вершина уголка находится в точке
(см.рис.),
следовательно, уголок, как и окружность, симметричен относительно оси ординат,
значит, если есть точка касания уголка и окружности в первой четверти,
то есть и точка касания во второй четверти. Следовательно, при
уголок и окружность имеют две общие точки, что нам не подходит. Тогда
остается только одно значение параметра
что соответствует
рисунку.
Значит, как говорилось выше, если и вершина уголка находится во
второй четверти, то правая ветвь касается окружности при
Следовательно,
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Получено верно одно из двух значений
параметра | 2 |
| ИЛИ | |
| Значения параметра найдены верно, но
также в ответ записаны лишние значения
параметра | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |



