Ошибка.
Попробуйте повторить позже
Есть четыре коробки с камнями: в первой коробке 121 камень, во второй — 122, в третьей — 123, а в четвёртой камней нет. За один ход берут по одному камню из любых трех коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Может ли в первой коробке оказаться 121 камень, во второй — 122, в третьей — 119, а в четвёртой 4 камня?
б) Может ли в последней коробке быть 366 камней?
в) Какое максимальное число камней может быть в четвертой коробке?
Источник:
а) Покажем как переместить ровно четыре камня из третьей коробки в четвертую:
б) Рассмотрим разность числа камней в четвертой и первой коробках. Пусть в первой сейчас камней, в четвертой
камней. Тогда
разность равна
. Если мы переложим три камня в первую коробку, то разность будет равна
. Если мы
переложим три камня во вторую коробку, то разность будет равна
. Если мы переложим три камня в третью
коробку, то разность будет равна
. Если мы переложим три камня в четвертую коробку, то разность будет равна
. Мы получили, что после любой операции разность либо изменяется на 4, либо остается прежней, то есть после
любых операций разность должна измениться на число, кратное 4. Тогда, если в четвертой коробке после некоторых операций могли
оказаться все камни (их всего
), то в конце разность должна быть равна
. Изначально разность была
равна
, значит, она изменилась на
. 487 не делится на 4, значит, в четвертой коробке не могли оказаться
366 камней.
в) Аналогично предыдущему пункту мы можем доказать, что разность между любыми двумя коробками может измениться только на
число, кратное 4. Тогда посмотрим на изначальную разность между первой и второй коробками. Она равна . Разность
между третьей и второй равна
. Тогда, если в первой коробке после всех операций не оказалось камней,
то во второй и в третьей коробках лежит хотя бы по 1 и 2 камня соответственно, то есть в первых трех коробках есть
хотя бы 3 камня. Если в первой один камень, то во второй есть хотя бы 2 камня, то есть количество камней хотя бы 3.
Если в первой коробке 2 камня, то во второй коробке есть хотя бы 3 камня, то есть количество камней в первых трех
коробках не меньше 5. Если в первой коробке есть хотя бы 3 камня, то в первых трех коробках уже точно есть хотя бы 3
камня.
Значит, в четвертой коробке не больше 363 камней. Покажем как можно добиться этого. Переложим из третьей коробки 120 камней в
четвертую с помощью операций из пункта а). Получим ситуацию .
Теперь аналогично будем перекладывать по 4 камня из второй коробки в четвертую:
С помощью таких операций переложим 116 камней. Получим ситуацию . Теперь аналогично будем перекладывать по 4
камня из первой коробки в четвертую:
С помощью таких операций переложим 116 камней. Получим ситуацию .
Далее так:
а) Да
б) Нет
в) 363
Ошибка.
Попробуйте повторить позже
Пусть , может ли при этом выполняться равенство
?
Пусть , тогда
.
Ошибка.
Попробуйте повторить позже
Составьте из цифр магический квадрат, то есть разместите их в квадратной
таблице так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.
Вот способ расстановки:
Ошибка.
Попробуйте повторить позже
Известно, что . Можно ли расставить в квадрат
числа
,
,
так, чтобы суммы
чисел по всем строкам и всем столбцам были различны?
Ошибка.
Попробуйте повторить позже
Во время похода Лосяш отправился к речке за водой. У него есть только 2 ведра емкостью 9 литров и 4 литра, а ему для супа нужно отмерить ровно 5 литров воды. Как Лосяшу справиться с этим заданием? Ведра у Лосяш причудливой формы, поэтому на глаз он умеет только определять, пустое ведро или полное.
Сначала набираем полное 9-литровое ведро. Затем выливаем из него воду в
4-литровое, пока то не заполнится до краев. Как только это случилось, в
9-литровом ведре осталось ровно литров воды — ровно столько, сколько
нужно для супа.
Ошибка.
Попробуйте повторить позже
Крош подарил Нюше два бикфордовых шнура: такой шнур горит неравномерно и сгорает ровно за 1 минуту. Как Нюше при помощи двух таких шнуров и зажигалки отмерить ровно 45 секунд?
Подожжем первый шнур с двух концов, а второй шнур с одного. Когда первый
шнур целиком догорит, пройдет ровно 30 секунд, значит, второму шнуру, если
ничего не изменится, также останется гореть 30 секунд. Но в этот момент мы
подожжем его со второго конца. Тогда он догорит в два раза быстрее, то есть за 15
секунд. В итоге второй шнур горел всего секунд, именно это время
нам и требовалось отмерить.
Ошибка.
Попробуйте повторить позже
Четырем трудолюбивым бурундучкам привезли 5 четырехколесных грузовиков. К сожалению, на них до сих пор стоит летняя резина, а на дворе уже почти зима. Поэтому бурундучкам надо срочно поменять на каждом колесе резину на зимнюю. Один бурундучок меняет резину на одном колесе за один час. К сожалению, менять резину на двух или более колесах одного грузовика одновременно нельзя. Могут ли 4 бурундучка поменять резину на всех 5 грузовиках за 5 часов?
Приведем один из возможных примеров, как бурундучкам справиться с этой работой. Пронумеруем грузовики числами 1, 2, 3, 4 и 5. Расставим эти грузовики мысленно по кругу так, чтобы после пятого грузовика шел первый. Пусть за первый час бурундучки поменяют по одному колесу на грузовиках с номерами 1, 2, 3 и 4. Затем бурундучки переходят к следующим по часовой стрелке грузовикам и за второй час меняют по одному колесу на грузовиках 2, 3, 4 и 5. В третий час они меняют по одному колесу на грузовиках с номерами 3, 4, 5, 1. В четвертый час — на грузовиках с номерами 4, 5, 1 и 2, и, наконец, за пятый час они меняют колеса на грузовиках с номерами 5, 1, 2 и 3. Заметим, что над каждый грузовиком трудились ровно 4 часа. Значит, все 4 колеса бурундучки успели поменять.
Ошибка.
Попробуйте повторить позже
В ромашковой долине открывается новое 20-этажное здание. В лифте есть всего две кнопки: при нажатии первой лифт поднимается на 13 этажей, а при нажатии второй лифт спускается на 8 этажей. При этом если нажать первую кнопку выше 7-го этажа или вторую кнопку ниже 9-го, то лифт ломается. Как с помощью такого инновационного лифта попасть с 13-го этажа на 8-й?
Приведем последовательность этажей, начиная с 13-го и заканчивая 8-м, на которые надо ездить. При этом если следующий этаж выше текущего, то нажимать надо первую кнопку, а если выше, то вторую:
Обратите внимание, что алгоритм единственный: с любого этажа этого здания можно поехать либо только наверх, либо только вниз, поэтому в любой момент следующий этаж определяется однозначно.
Ошибка.
Попробуйте повторить позже
Целое число является суммой не менее пяти последовательных членов непостоянной арифметической прогрессии, состоящей
из целых чисел.
a) Может ли равняться 9?
б) Может ли равняться 2?
в) Найдите все значения, которые может принимать
а) Да, может равняться 9, если взять числа
0, 1, 2, 3, 4. Тогда
б) Пусть 2 является суммой членов арифметической прогрессии с начальным членом
и шагом
Тогда
Заметим, что — целое число, значит,
тоже целое. Тогда
— делитель 4, то есть
По
предположению
Противоречие.
в) Предствим любое натуральное число в виде суммы хотя бы пяти последовательных членов арифметической
прогрессии. Рассмотрим последовательность
…,
При
в такой последовательности не меньше
шести членов, значит, она подходит под условие. Найдем ее сумму:
Если мы заменим числа на противоположные по знаку, то получим отрицательное число, значит, можем принимать все
целые значения, которые больше 2 по модулю, то есть
По предыдущему пункту мы не можем получить число 2, значит, аналогично можем доказать, что число мы тоже не
сможем получить.
Пусть 1 является суммой членов арифметической прогрессии с начальным членом
и шагом
Тогда
Заметим, что — целое число, значит,
тоже целое. Тогда
— делитель 2, то есть
По
предположению
Противоречие. Аналогично докажем, что и число
мы тоже не сможем получить.
Число 0 можно получить последовательностью Значит,
а) Да
б) Нет
в)
| Содержание критерия | Балл |
| Обоснованно получены верные ответы в пунктах а), б) и в) | 4 |
| Обоснованно получен верный ответ в пункте в) и обоснованно получен верный ответ в пунктах а) или б) | 3 |
| Обоснованно получены верные ответы в пунктах а) и б), | 2 |
| ИЛИ | |
| обоснованно получен верный ответ в пункте в) | |
| Обоснованно получен верный ответ в пунктах а) или б) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Будем называть четырёхзначное число очень счастливым, если все цифры в его десятичной записи различны, а сумма первых двух цифр равна сумме последних двух цифр. Например, очень счастливым является число 3140.
а) Существуют ли двадцать последовательных четырёхзначных чисел, среди которых есть три очень счастливых?
б) Может ли разность двух очень счастливых четырёхзначных чисел равняться 2016?
в) Найдите наименьшее простое число, для которого не существует кратного ему очень счастливого четырёхзначного числа.
а) Примером двадцати таких чисел является последовательнось 5014, 5015, …, 5032, 5033. Среди этих чисел есть три очень счастливых: 5014, 5023 и 5032.
б) Предположим, что разность двух очень счастливых четырёхзначных чисел может равняться 2016. Пусть —
десятичная запись меньшего из них, а
— десятичная запись большего из них.
Из условия следует, что либо либо, если при сложении
и 2016 в разряде десятков был переход
через десяток,
Тогда
Значит, число даёт при делении на 9 или остаток 7, или остаток 6.
Аналогично из условия следует, что либо либо
Тогда
Значит, число даёт при делении на 9 или остаток 2, или остаток 3. По условию
Но числа и
дают разные остатки при делении на 9. Противоречие.
в) Покажем, что искомое простое число равно 11. Для начала приведем пример очень счастливого четырёхзначного числа, которое делится на 2, 3, 5 и 7 — число 1890.
Теперь докажем, что не существует очень счастливого четырёхзначного числа, кратного 11. Пусть — запись
какого-либо очень счастливого числа, которое делится на 11. Тогда
Значит, число кратно 11. Поскольку
и
— цифры, отсюда следует, либо
либо
либо
В первом случае имеем и
Вычитая эти равенства, получаем
то есть
—
противоречие, поскольку все цифры должны быть различны.
Во втором случае и
Вычитая эти равенства, получаем
то есть
— тоже противоречие, так как 11 не кратно 2. Аналогичное противоречие получается и в третьем случае. Значит,
не существует очень счастливых четырёхзначные чисел, кратных 11.
а) Да
б) Нет
в) 11
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
а) Дана таблица в которой расставлены попарно различные натуральные числа от 1 до 9. Разрешается
производить следующую операцию: выбирается какая-то клетка, все числа в клетках, которые граничат с выбранной по
стороне, уменьшаются на 1, а значение в выбранной клетке увеличивается на число, равное количеству клеток,
соседних с выбранной по стороне. Могла ли после нескольких таких операций сумма чисел в таблице стать равной
40?
б) В таблице снова расставлены попарно различные числа от 1 до 9. Для каждой строки таблицы вычислили
произведение чисел в ней, затем три полученных произведения сложили. Могло ли в результате получиться число
442?
в) Теперь в таблице расставили девять произвольных различных натуральных чисел так, что произведения чисел в
любом столбце и в любой строке одинаковые. Какое наименьшее значение может принимать наибольшее из этих чисел в
таблице?
а) Докажем, что после операции сумма чисел в таблице не изменяется. Будем называть «соседними» те клетки, которые граничат с выбранной клеткой по стороне.
Если у выбранной клетки было соседних клеток, а сумма всех чисел в таблице была равна
то после уменьшения чисел
в соседних клетках на 1 сумма чисел во всей таблице стала равняться
Тогда после увеличения числа в выбранной клетке
на
сумма чисел во всей таблице снова стала равняться
Изначально сумма чисел в таблице была равна Значит, после любого количества операций она останется равной
45.
б) Да, так могло получиться, если в первой строчке стояли числа 1, 5, 8. Во второй — числа 2, 3, 4. В третьей — числа 6, 7, 9. Тогда полученное число равно
в) В таблицу расставлено 9 натуральных чисел, значит, одно из них хотя бы 9. Будем вести перебор по наименьшему значению наибольшего числа.
Пусть можно расставить натуральные числа от 1 до 9 так, как это сказано в условии. Рассмотрим эту расстановку. Обратим внимание на число 7. Так как оно присутствует в таблице, то произведение хотя бы в одном столбце делится на 7. Значит, произведение чисел в любом столбце и в любой строке делится на 7. Заметим, что в таблице всего одно число, которое делится на 7, следовательно, в двух столбцах из трех нет числа, которое делится на 7. Тогда произведение в них не делится на 7. Противоречие. Значит, либо должно быть хотя бы три числа, которые делятся на 7, либо их не должно быть вовсе. Если такие три числа есть, то в таблице точно есть число не меньше 21. Пусть в таблице нет чисел, которые делятся на 7.
Пусть можно расставить натуральные числа 1, 2, 3, 4, 5, 6, 8, 9, 10 так, как это сказано в условии. Рассмотрим эту расстановку. Обратим внимание на числа 5 и 10. Так как они присутствуют в таблице, то произведение хотя бы в одном столбце делится на 5. Значит, произведение чисел в любом столбце и в любой строке делится на 5. Заметим, что в таблице всего два числа, которые делятся на 5, следовательно, в каком-то из трех столбцов нет числа, которое делится на 5. Тогда произведение в нем не делится на 5. Противоречие. Значит, либо должно быть хотя бы три числа, которые делятся на 5, либо их не должно быть вовсе. Если такие три числа есть, то в таблице точно есть число не меньше 15.
Пусть в таблице нет чисел, которые делятся на 5. Тогда оценим наименьшее значение наибольшего числа в таблице, взяв девять самых маленьких натуральных чисел, которые мы можем брать. Значит, в таблице расставлены числа 1, 2, 3, 4, 6, 8, 9, 11, 12.
Заметим, что с числом 11 можно провести рассуждения, аналогичные рассуждениям с 7. Тогда либо в таблице есть число не меньше 33, либо нет чисел кратных 11.
Если таких чисел нет, то минимальные девять чисел это 1, 2, 3, 4, 6, 8, 9, 12, 13. Но с 13 можно провести аналогичные 7 рассуждения. Тогда минимальное возможное наибольшее число равно 15, потому что если есть число 14, то есть и число не меньше 21. Но 15 делится на 5, значит, среди чисел таблицы есть еще числа 5 и 10.
Тогда произведение в каждом столбце и строке должно делиться на 5. Для этого поставим числа 5, 10 и 15 в клетки одной из диагоналей. Тогда произведение в столбцах и строках должно делиться на 10 и на 15, то есть на 30.
Тогда будем пробовать строить пример на произведение, кратное 30. Для произведения 120 получим следующую расстановку:
а) Нет
б) Да
в) 15
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в пункте а); — пример в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
В роте два взвода, в первом взводе солдат меньше, чем во втором, но больше, чем 50, а вместе солдат меньше, чем 120. Командир знает, что роту можно построить по несколько человек в ряд так, что в каждом ряду будет одинаковое число солдат, большее 7, и при этом ни в каком ряду не будет солдат из двух разных взводов.
а) Сколько солдат в первом взводе и сколько во втором? Приведите хотя бы один пример.
б) Можно ли построить роту указанным способом по 11 солдат в одном ряду?
в) Сколько всего солдат может быть в роте?
Пусть в первой роте солдат, во второй —
Запишем условия на
и
которые нам даны.
Далее идет условие про построение в ряды. Поймем, что оно на самом деле для нас означает. В каждом ряду могут
стоять солдаты только одной роты, то есть ряды могут быть двух типов: только из солдатов первой роты, либо только
из солдатов второй. Пусть в ряду человек, рядов первого типа
второго
тогда ясно, что
Таким образом мы поняли, что условие про ряды фактически означает, что существует некоторое
такое, что
и
а) Подойдут, например, количества солдат 54 в первом взводе и 63 во втором взводе при
б) Заметим, что
То есть более полным и удобным для нас комплектом условий будет
Эти условия можно сформулировать так: и
это два числа, кратные некоторому
лежащие между 50 и 70 и имеющие сумму
меньше 120.
Проверим, может ли быть равно 11. Только два числа между 50 и 70 кратны 11 — 55 и 66, но их сумма больше 120. Значит, такого
быть не может.
в) Будем перебирать по начиная с 8, наверх и рассматривать все возможные натуральные
кратные этому
При подходят только 56 и 64, но их сумма не меньше 120.
При подходят только 54 и 63, они подходят, их сумма 117.
При подходит только 60.
При по пункту б) нет возможных вариантов.
При подходит только 60.
При подходят 52 и 65, их сумма 117.
При подходит только 56.
При подходит только 60.
При подходит только 64.
При подходят 51 и 68, их сумма 119.
При подходит только 54.
При подходит только 57.
Дальше перебирать нет смысла, т.к. чтобы два различных числа были кратны некоторому их разность должна быть не меньше
20, значит, они не могут одновременно лежать в интервале
Итого, общее количество людей может быть равно 117 или 119.
а) 54 и 63 соответственно
б) Нет
в) 117 или 119
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
По кругу в некотором порядке по одному разу написаны числа от 9 до 18. Для каждой из десяти пар соседних чисел нашли их наибольший общий делитель.
а) Могло ли получиться так, что все наибольшие общие делители равны 1?
б) Могло ли получиться так, что все наибольшие общие делители попарно различны?
в) Какое наибольшее количество попарно различных наибольших общих делителей могло при этом получиться?
а) Да, например, числа на круге можно расположить так:
![]()
б) Рассмотрим число 13. Оно простое и взаимно просто со всеми остальными числами, следовательно, оба НОДа с его участием будут равны 1. Значит, такое невозможно.
в) Рассмотрим числа 11, 13 и 17. Они простые и взаимно просты со всеми остальными числами, следовательно, все НОДы с их участием будут равны 1. Пусть они стоят по кругу в некотором порядке. Каждое из чисел участвует ровно в двух НОДах.
Пусть — количество пар соседних среди наших чисел, тогда очевидно, что
а количество НОДов единичек не менее
чем
Всего 10 НОДов, среди которых хотя бы 4 единицы, значит, различных НОДов не более чем
7.
Построим пример с учетом знания того, что для достижения максимума числа 11, 13 и 17 должны стоять подряд:
![]()
а) Да
б) Нет
в) 7
Ошибка.
Попробуйте повторить позже
На доске написаны несколько целых чисел. Несколько раз с доски стирали по два числа, сумма которых делится на 5.
а) Может ли сумма всех оставшихся на доске чисел равняться 20, если сначала по одному разу были написаны числа 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13?
б) Может ли на доске остаться ровно два числа, разность между которыми равна 45, если сначала по одному разу были написаны все натуральные числа от 103 до 208 включительно?
в) Известно, что на доске осталось ровно два числа, а сначала по одному разу были написаны все натуральные числа от 103 до 208 включительно. Какое наибольшее значение может получиться, если поделить одно из оставшихся чисел на второе из них?
а) Да, может. Пусть стерты оказались пары
Тогда остались числа 2, 3, 5, 10 с суммой 20.
б) Заметим, что число, кратное 5, может быть стерто в паре только с другим числом, кратным 5. Таким образом, четность количества чисел, кратных 5, не меняется после стираний.
Посчитаем, сколько чисел, кратных 5, содержится среди чисел от 103 до 208. Наименьшее из них, кратное 5, равно 105, наибольшее — 205. Тогда всего чисел, кратных 5, будет ровно
Пусть остались числа и
Тогда хотя бы одно из них должно делиться на 5, так как 21 нечетно и хотя бы одно
кратное 5 число не будет вычеркнуто, но тогда и второе должно делиться 5, так как
Значит, каким-то образом
последовательность вычеркиваний изменила количество чисел, кратных 5, с 21 до 2, что противоречит факту про четность,
доказанному выше.
в) Посчитаем количество чисел с каждым из остатков по модулю 5 среди чисел от 103 до 208, то есть заменим числа на их остатки по модулю 5 и посчитаем количество каждого из остатков. Так как число 103 дает остаток 3 по модулю 5, то блок длины 5, который будет повторяться, начинается с 3:
Всего от 103 до 208 включительно 106 чисел. Количество таких полных блоков равно 21 как целая часть от деления
Остаток равен 1, следовательно, после последнего цельного блока будет стоять остаток 3 и ему соответствует последнее число
208. Получаем, что остаток 3 встречается 22 раза, остатки 4, 0, 1 и 2 по 21 разу.
В пункте б) мы уже доказали, что среди двух оставшихся чисел будет хотя бы одно, кратное 5. Кроме того, хотя бы одно будет давать остаток 3, так как число, дающее остаток 3, должно вычеркиваться в паре с числом, дающим остаток 2, при этом остаток 3 дают 22 числа, а остаток 2 — только 21 число.
Мы доказали, что из двух оставшихся чисел одно будет делиться на 5, а второе — давать остаток 3. Разберем два случая:
- Большее из чисел дает остаток 3. Мы хотим максимизировать отношение, значит, мы должны минимизировать
меньшее число и максимизировать большее. Наибольшее число с остатком 3 — это 208, наименьшее с остатком 0
— 105, тогда в этом случае максимальное отношение равно
- Большее из чисел дает остаток 0. Мы хотим максимизировать отношение, значит, мы должны минимизировать
меньшее число и максимизировать большее. Наибольшее число с остатком 0 — это 205, наименьшее с остатком 3
— 103, тогда в этом случае максимальное отношение равно
Сравним полученные дроби:
Тогда наибольшее значение равно
а) Да
б) Нет
в)
| Содержание критерия | Балл |
| Обоснованно получены верные ответы в пунктах а), б) и в) | 4 |
| Обоснованно получены верные ответы в пунктах а) и б), либо обоснованно получены верные ответы в пунктах а) и в) | 3 |
| Обоснованно получен верный ответ в пункте б), пункты а) и в) не решены | 2 |
| ИЛИ | |
| обоснованно получен верный ответ в пункте в), пункты а) и б) не решены | |
| Приведён пример в пункте а), пункты б) и в) не решены | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Пираты нашли сундук с сокровищами, в котором было 60 монет достоинством 1 дукат и 60 монет достоинством 5 дукатов.
а) Получится ли поделить все деньги поровну между 18 пиратами, если каждому должно достаться целое число монет, а сдачи и размена ни у кого из пиратов нет?
б) Получится ли поделить все деньги поровну между 40 пиратами, если каждому должно достаться целое число монет, а сдачи и размена ни у кого из пиратов нет?
в) При каком наибольшем количестве пиратов капитану всегда удастся поделить монеты между ними, каким бы способом ему ни захотелось это сделать (возможно, кому-то из пиратов будет полагаться 0 монет)?
a) Каждый пират должен получить количество дукатов, равное
Выдадим 15 пиратам по 4 монеты достоинством 5 дукатов, троим — по 20 монет достоинством 1 дукат.
б) Каждый пират должен получить количество дукатов, равное
Тогда нужно будет выдать каждому не менее 4 монет достоинством 1 дукат. Значит, всего монет достоинством 1 дукат нужно не менее 160 штук, а в сундуке их только 60. Следовательно, без сдачи и размена поделить все монеты поровну не получится.
в) Рассмотрим случай, когда пиратов 17 или больше. Приведём пример раздела, который капитан не сможет реализовать.
Пусть капитан хочет достичь следующего раздела: 16 пиратов должны получить по 4 дуката, один — все оставшиеся деньги, остальные, если они есть, — ничего. Тогда распределить монеты нельзя по тем же причинам, что и в пункте б).
Пусть пиратов 16. Покажем, как реализовать произвольный раздел. Заметим, что если некоторый раздел можно осуществить с помощью монет по 5 дукатов, то его можно осуществить и с помощью монет по 5 и по 1 дукату (при том, что сумма денег одна и та же), просто формируя пятерки из единиц.
Пусть некоторому пирату полагается дукатов. Выдадим ему количество
дукатов, равное остатку числа
по модулю 5, монетами по 1 дукату. Произведем
эту операцию с каждым пиратом.
Сумма таких остатков для всех пиратов должна быть кратна 5, так как общая
сумма денег кратна 5. Также эта сумма не больше чем так как
каждому пирату придется выдать не более 4 монет по одному дукату, ведь остаток
числа при делении на 5 не превышает 4. Наибольшее натуральное число, не
превышающее 64 и кратное 5, равно 60. Значит, для описанной процедуры точно
хватит монет по 1 дукату.
После вышеописанного каждому пирату недовыдано некоторое количество монет, кратное 5. Тогда очевидно, что оставшиеся монеты можно распределить нужным образом.
а) Да, получится
б) Нет, не получится
в) 16
| Содержание критерия | Балл |
| Получены верные обоснованные ответы в пунктах а), б) и в) | 4 |
| Получены верные обоснованные ответы в пунктах а) и б), либо получены верные обоснованные ответы в пунктах а) и в) | 3 |
| Получен верный обоснованный ответ в пункте б), пункты а) и в) не решены, либо получен верный обоснованный ответ в пункте в), пункты а) и б) не решены | 2 |
| Приведен пример в пункте а), пункты б) и в) не решены | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
На участке высадили ясени и дубы, причем всего было высажено больше 14 деревьев. Если бы ясеней посадили в два раза больше, а дубов — на 20 больше, то дубов было бы больше, чем ясеней. Если же дубов станет в два раза больше, а количество ясеней увеличится на 2, то ясеней будет больше, чем дубов.
а) Могли ли посадить 12 ясеней и 6 дубов?
б) Могли ли посадить 13 ясеней и 6 дубов?
в) Какое наибольшее число дубов могли посадить?
Обозначим количество ясеней через , количество дубов через
. Запишем систему неравенств, отражающую все условия
задачи
|
|
а) Проверим, является ли пара решением системы.
|
|
Все условия удовлетворены, значит, такое возможно.
б) Проверим, является ли пара решением системы.
|
|
При таком количестве дубов и ясеней нарушается второе неравенство системы, значит, такого быть не могло.
в) Из второго неравенства системы получим
|
|
Объединяя результат с третьим неравенством системы, получим
Мы доказали, что количество дубов не должно превышать 8. Попробуем найти такое количество ясеней, чтобы при 7
дубах все неравенства системы были удовлетворены. Для этого просто подставим в систему
и решим ее относительно
.
При 13 ясенях и 7 дубах все условия выполняются, следовательно, максимально возможное количество дубов равно 7.
а) Да
б) Нет
в) 7
| Содержание критерия | Балл |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов. | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов. | 2 |
| Верно получен один из следующий результатов: — обоснованное решение в пункте а); — обоснованное решение в пункте б); — искомая оценка в пункте в); — пример в пункте в), обеспечивающий точность предыдущей оценки. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
У Игоря есть гири с массами ,
,
,
...,
.
а) Может ли Игорь уравновесить чашечные весы, использовав все гири разом?
б) Сможет ли Игорь уравновесить чашечные весы, использовав все гири, которые у него будут, когда
Тимур подарит ему гирю с массой ?
а) Сумма масс имеющихся у Игоря гирь:
– нечётна, следовательно, имеющиеся у Игоря гири нельзя поставить на весы так, чтобы чаши
уравновесились.
б) Так как теперь гирь , то их нельзя разбить на пары. Тогда возьмём и
отложим в сторону гири с массами
,
и
.
Разберёмся сначала с остальными гирями – их уже можно разбить на пары так, чтобы
суммарные массы во всех парах были одинаковы: ,
, ...,
– всего
пар. Теперь можно на одну чашу весов положить все гири, которые попали в
первые
пары, а на другую чашу весов все остальные гири, кроме гирь с массами
,
и
.
На данный момент весы находятся в равновесии, а не использовали мы только те самые гири с
массами ,
и
. Остаётся только гирю с массой
положить на одну чашу весов (любую), а гири с
массами
и
– на другую чашу весов.
а) Нет
б) Да
Ошибка.
Попробуйте повторить позже
Можно ли расставить в квадрат числа
,
,
так, чтобы суммы чисел по всем строкам и всем
столбцам были различны?
Сумма восьми каких-нибудь чисел из множества может быть равна
,
,
, ...,
или
.
Пусть
– сумма чисел в
-ой строке,
– сумма чисел в
-ом столбце, тогда среди чисел
, ...,
,
, ...,
должны встретиться все числа из множества
, кроме
одного.
При этом , так как обе эти суммы есть просто сумма всех чисел в данной
квадратной таблице. Тогда можно попробовать положить
,
,
,
,
,
,
,
,...,
,
,
,
.
Соответствующий способ заполнения квадратной таблицы приведён ниже:
Ошибка.
Попробуйте повторить позже
На доске записаны числа . Разрешается стереть любые два числа и вместо них записать
их разность – неотрицательное число. Может ли на доске в результате нескольких таких операций
остаться только число 15?
Вот как это можно сделать:
Ошибка.
Попробуйте повторить позже
Можно ли расположить одинаковых монет вдоль стенок большой квадратной коробки так, чтобы
вдоль каждой стенки лежало ровно
а) по монеты;
б) по монеты;
в) по монеты;
г) по монет;
д) по монет;
е) по монет?
(Разрешается класть монеты одну на другую).
а) Заметим, что если вдоль каждой стенки будет стоять по две монеты, то всего монет будет не больше
, а у нас их
, значит нельзя.
б)–д) В этих пунктах можно расположить монеты требуемым образом. Примеры расстановки приведены
на рисунках: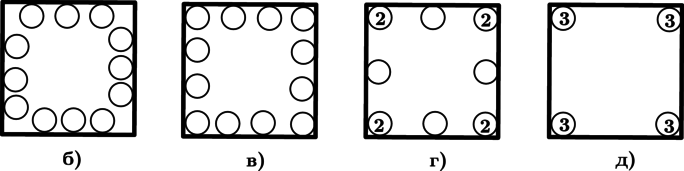
г) Заметим, что каждая монета может стоять максимум около двух стенок коробки, и даже если мы
поставим по монет одна на другую (оптимальная расстановка), то всего монет будет
, а у нас их
– противоречие.



