Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно одно решение.
Сделаем замену , тогда новое уравнение
также должно иметь единственное решение. Рассмотрим функцию , определенную при
Производная
Производная положительна при и отрицательна при
.
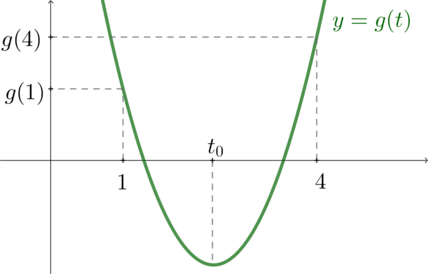
Так как при
и
, то схематично график функции выглядит следующим образом:
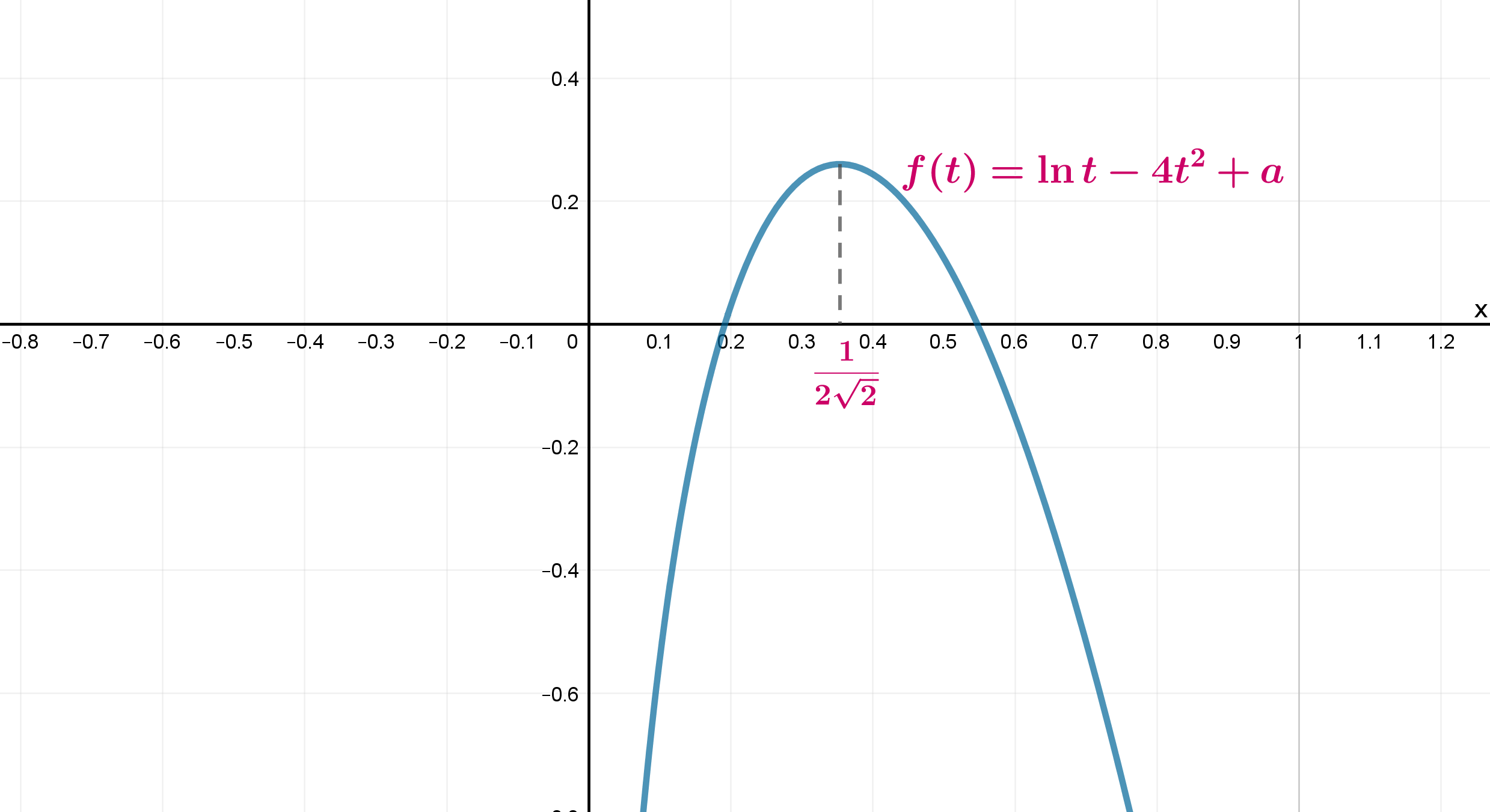
Следовательно, единственное решение уравнение имеет в том случае, когда , где
:
Ошибка.
Попробуйте повторить позже
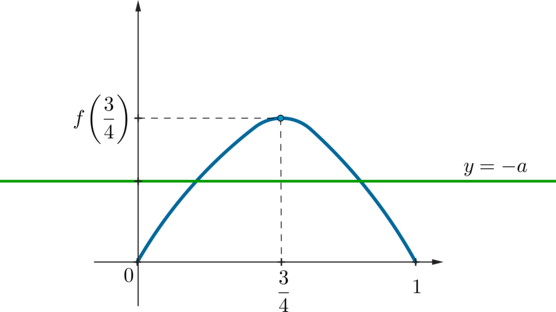
При каких значениях параметра уравнение
имеет решения?
Применим формулу косинуса двойного угла и умножим обе части уравнения на
, наложив дополнительное условие
:
Сделаем замену с условиями
. Рассмотрим
функцию
Проверим монотонность функции на отрезке
. Нас интересует
поведение функции и наличие корней только на этом отрезке. Имеем
Тогда функция монотонно возрастает на отрезке
.
Посмотрим, какие условия должны выполняться, чтобы уравнение
имело хотя бы один корень (на самом деле из монотонности следует, что не более
одного) на отрезке
. Временно забудем про ограничение
, в конце
выкинем лишние значения.
Во-первых, значение функции в левом конце отрезка должно быть не больше
нуля, то есть . Действительно, ведь в противном случае на всем отрезке
график функции
будет лежать выше оси абсцисс, а значит, на этом
отрезке не будет корней.
Во-вторых, значение функции в правом конце отрезка должно быть не меньше
нуля, то есть , иначе график функции окажется ниже оси абсцисс на
рассматриваемом отрезке.
При выполнении двух перечисленных условий мы гарантированно будем иметь
ровно один корень на отрезке . Получаем систему
Осталось найти и выколоть значение , при котором
является
решением уравнения
. Тогда это
. Итого, получаем
При всех найденных будет существовать решение для
, а значит и для
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование либо исследования функции, либо перехода к системе | 3 |
| Верный переход к системе неравенств, но либо есть ошибка при
их исследование, либо не учтено, что | 2 |
| Верное введение и исследование функции | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых функция
имеет хотя бы одну точку максимума.
Раскроем модуль:
Таким образом, графиком функции является объединение части левой параболы, соответствующей
, и части правой параболы, соответствующей
. Заметим, что эти части “соединяются” в одной точке
.
Так как у параболы одна убывающая и одна возрастающая ветвь, то от каждой параболы можно взять либо только строго
монотонную ветвь, либо часть, состоящую из обеих ветвей, то есть и возрастающей, и убывающей. Следовательно, график
можно выглядеть одним из четырех способов:
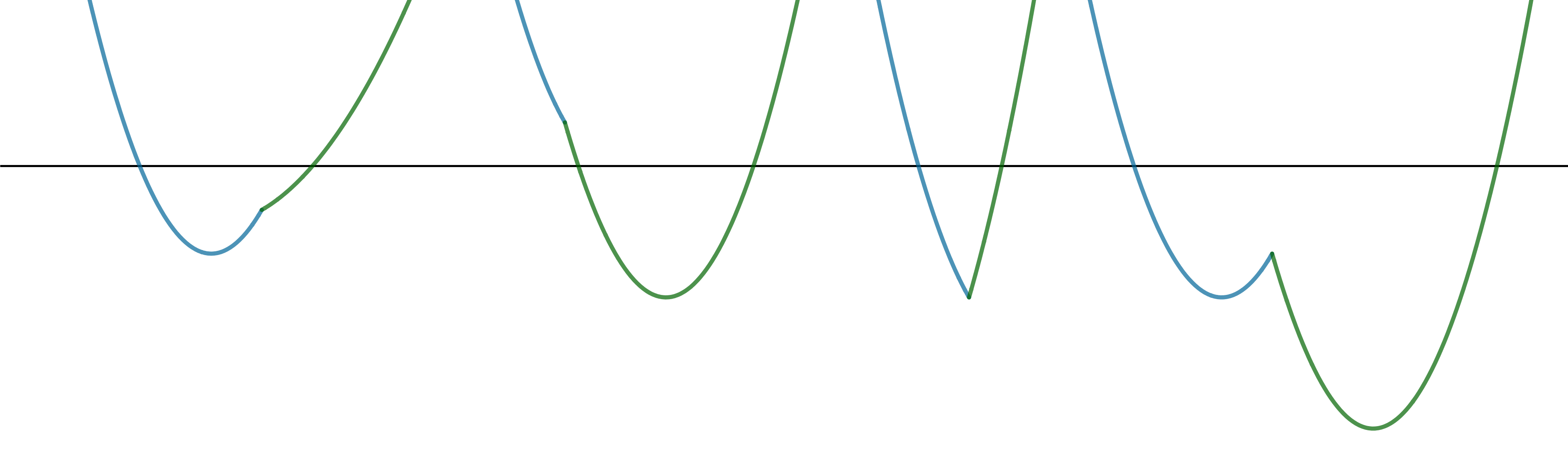
Так как точка максимума — это такая точка , в некоторой окрестности которой функция меняет свой характер
монотонности с возрастания на убывание, то есть при некотором
для всех
функция возрастает, а для
всех
убывает, то точка максимума имеется только на последнем рисунке. Последний рисунок задается тем,
что абсцисса
вершины левой параболы строго левее
, а абсцисса
вершины правой параболы — строго
правее
, то получаем следующее условие на параметр
Ошибка.
Попробуйте повторить позже
Найдите все пары , при которых множество решений неравенства
Перепишем неравенство в виде
Рассмотрим две функции и
. Заметим, что они зависят от разных параметров,
следовательно, графики функций не зависят друг от друга. График
получается из графика
сжатием/растяжением в
раз и сдвигом по оси ординат на
единиц. Изобразим схематично графики для некоторых зафиксированных параметров
и
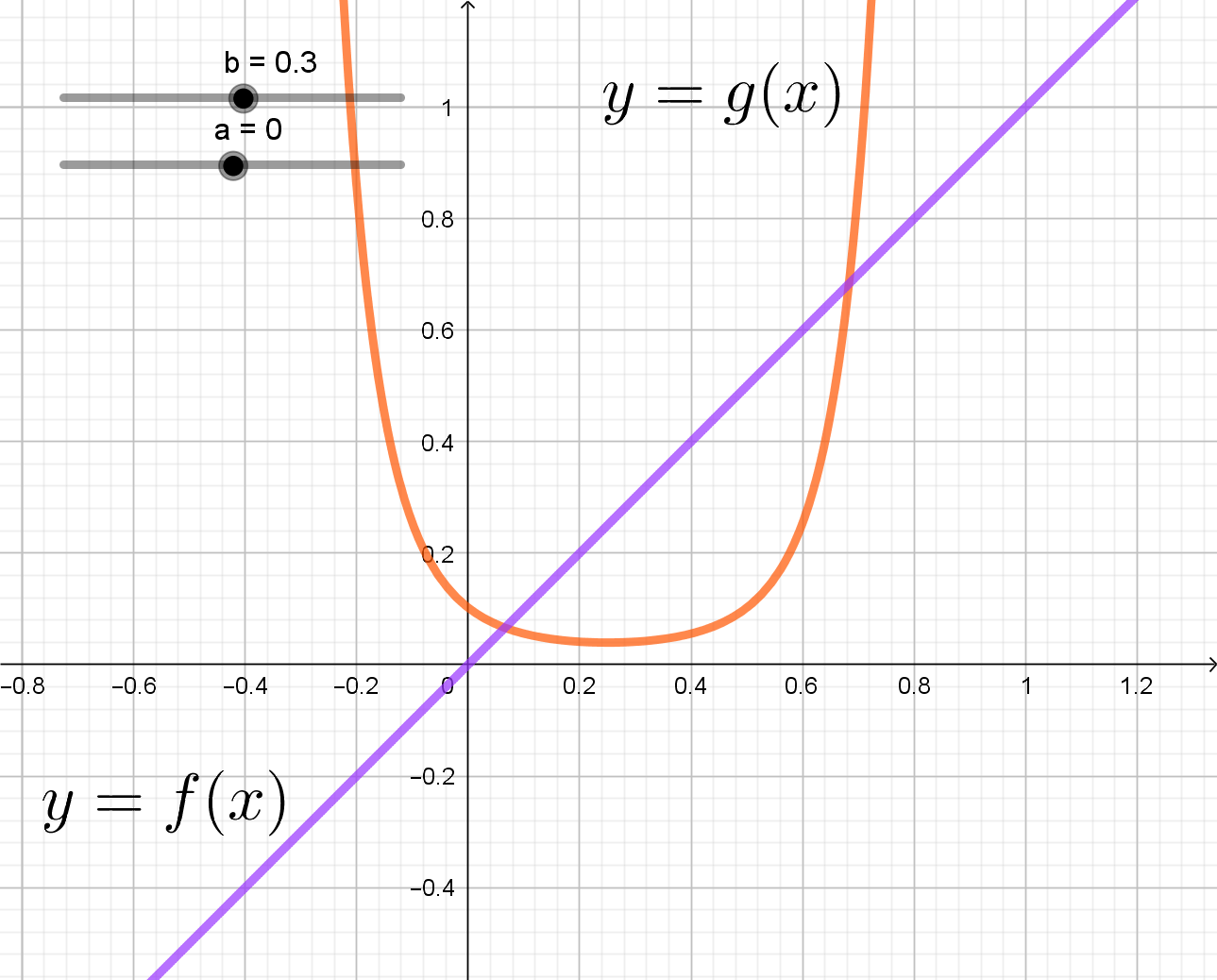
Множество решений состоит из тех , при которых прямая
находится выше графика функции
. Следовательно, две точки
пересечения этих графиков должны быть равны
, чтобы множеством решений был интервал
:
Ошибка.
Попробуйте повторить позже
При каких положительных не равных 1 значениях параметра неравенство
не имеет решений?
Перепишем неравенство в виде
Сделаем замену и исследуем ее. Заметим, что функция
четная
и определена при всех
Функция
при
возрастает и
положительна, функция
при
убывает, следовательно,
функция
убывает при Так как при
имеем
при
имеем
то получаем, что
После этой замены неравенство примет вид
Сделаем замену Тогда
а неравенство примет
вид
Следовательно, при
полученное неравенство не будет иметь
решений, если оно не имеет решений в принципе, то есть
либо все его
решения
При неравенство равносильно
Следовательно, для выполнения условия задачи необходимо, чтобы
Следовательно,
— первая часть ответа.
При неравенство равносильно
Следовательно, для выполнения условия задачи необходимо, чтобы
Следовательно,
— вторая часть ответа.
Таким образом, ответ
Ошибка.
Попробуйте повторить позже
АН уже не ребёнок, однако за свой тяжкий педагогический труд тоже
заслуживает подарка на Новый Год от Деда Мороза! К выбору подарка для АН
Дед Мороз подошёл оригинально: он помнил, что любимый номер АН в
профильном ЕГЭ по математике — номер с параметром — и выдумал
следующую параметрическую задачку.
Найдите все значения параметра , при каждом из которых модуль разности
ординат точек экстремума функции
больше 1296.
Начнём с рассмотрения случая
У постоянной функции нет точек экстремума, и разность между их ординатами быть больше 1296 не может.
Теперь рассмотрим случай
Найдем производную функции
Найдём критические точки производной (экстремумы):
Заметим, что вне зависимости от значения параметра абсциссы точек
экстремума неизменны. Следовательно, нам всего лишь следует решить такое
неравенство:
Вычислим значения функции в точках экстремума и решим получившееся неравенство:
Раскроем модуль по определению и получим:
для положительных значений неравенство
для отрицательных значений неравенство
решением которого
является
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены оба промежутка, входящие в ответ, с неверным включением—исключением концевых точек | 3 |
| С помощью верного рассуждения получен один промежуток, входящий в ответ | 2 |
| С помощью верного рассуждения получен один промежуток, входящий в ответ, с неверным включением—исключением концевых точек | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет шесть различных решений.
Сделаем замену ,
. Тогда уравнение примет вид
Заметим, что квадратное уравнение
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение
Очевидно, что если квадратное уравнение
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение имело два различных решения, его дискриминант должен быть
положительным:
2) Также нужно, чтобы оба корня были положительными (так как ). Если произведение двух
корней положительное и сумма их положительная, то и сами корни будут положительными.
Следовательно, нужно:
Таким образом, мы уже обеспечили себе два различных положительных корня и
.
3) Давайте посмотрим на такое уравнение
Рассмотрим функцию
Можно разложить на множители:
Если найти производную
Следовательно, график выглядит так:
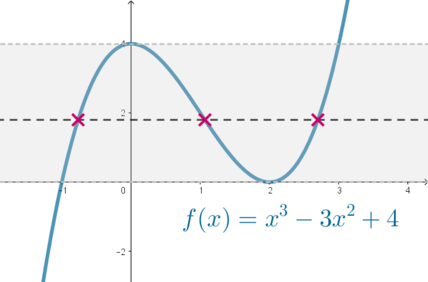
Мы видим, что любая горизонтальная прямая
Таким образом, нужно:
Систему
Таким образом, мы определили, что оба корня уравнения должны лежать в интервале
.
Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию . Ее график – парабола с ветвями вверх, которая
имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен
выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале
?
Так:
Во-первых, значения и
функции в точках
и
должны быть положительными,
во-вторых, вершина параболы
должна также находиться в интервале
. Следовательно, можно
записать систему:
Таким образом, нам нужно пересечь значения параметра , найденные в 1-ом, 2-ом и 3-ем пунктах,
и мы получим ответ:
Ошибка.
Попробуйте повторить позже
Пусть – решение неравенства
Для каждого целого значения параметра найдите максимальное значение функции
.
Сделаем замену для удобства: . Тогда неравенство примет вид:
Сделав обратную замену и учитывая, что , получим:
Преобразуем функцию, максимальное значение которой нужно найти:
Таким образом, функция примет вид:
Таким образом, графиком функции при каждом фиксированном значении является парабола,
ветви которой направлены вниз, а вершина параболы находится в точке
:
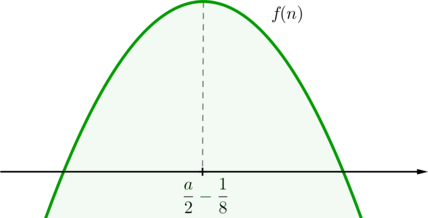
Рассмотрим параболу только при целых (так как, вообще говоря,
– целое).
ни при
каких целых
не будет являться целым числом. Следовательно, наибольшее значение функция
принимает точно не в вершине.
Рассмотрим два случая:
1) .
Тогда . Следовательно, парабола выглядит так:
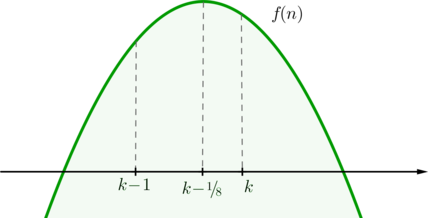
Заметим, что так как парабола симметрична относительно прямой , то чем ближе число
расположено к
, тем больше будет значение функции
в нем. Следовательно, максимальное
значение функция
будет принимать либо при
, либо при
. Заметим, что
находится ближе к
, чем
. Таким образом:
2) .
Тогда . Следовательно, парабола выглядит так:
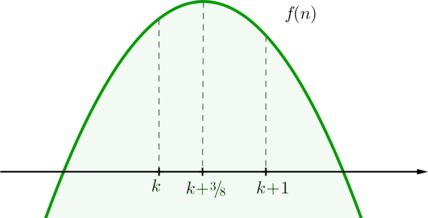
Аналогично, максимальное значение функция будет принимать либо при
, либо при
. Заметим, что
находится ближе к
, чем
. Таким образом:
при четном
при нечетном
Ошибка.
Попробуйте повторить позже
При каких значениях параметра уравнение
имеет решения.
1) Рассмотрим функцию .
Главный период у – это
, у
— это
, у
– это
. Тогда
главный период всей функции
– это НОК этих периодов, то есть
.
2) Для того, чтобы уравнение имело решения, необходимо, чтобы на любом отрезке длиной
выполнялось:
. Возьмем, например, отрезок
.
3) Найдем критические точки функции и построим ее схематичный график для того, чтобы понять,
чему равно и
.
Промежутку принадлежат точки
. Значит, знаки производной
такие:

Значит, минимальное значение на функция принимает в одной из точек
, а
максимальное — в одной из
.
Тогда на схематично функция выглядит так:

То есть . Значит,
.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет корни.
ОДЗ уравнения: . Следовательно, для того, чтобы уравнение имело корни,
нужно, чтобы хотя бы одно из уравнений
1) Рассмотрим первое уравнение
Таким образом, мы видим, что для любых уравнение будет иметь одно решение,
а для всех остальных – не будет иметь решений. Следовательно, при
уравнение
имеет решения.
2) Рассмотрим второе уравнение
Рассмотрим функцию . Найдем ее производную:
Заметим, что
Следовательно, для того, чтобы уравнение имело решения, нужно, чтобы график пересекался с
прямой
(на рисунке изображен один из подходящих вариантов). То есть нужно,
чтобы
3) Таким образом, изначальное уравнение будет иметь решения при или
. Объединяя эти решения, получим
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно два корня.
Рассмотрим три случая: ,
и
.
1) . Тогда уравнение примет вид
. Решим его графически. Рассмотрим
функцию
. Нули функции:
. Производная равна
, следовательно,
точки экстремума
, причем
– точка максимума,
– точка минимума.
Следовательно, график выглядит так:
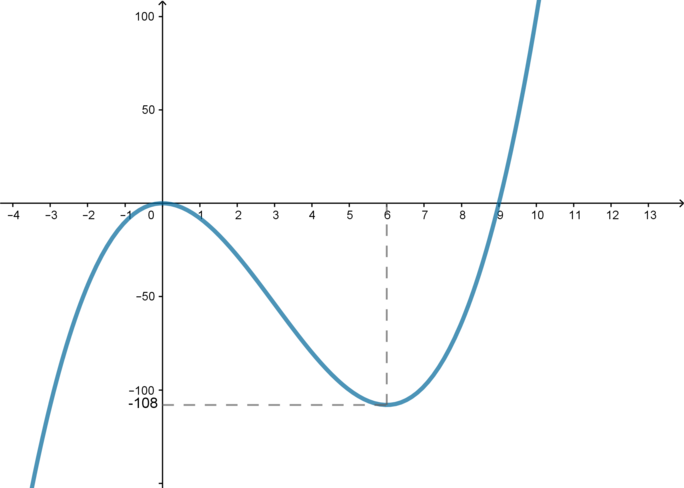
Причем . Следовательно, решение уравнения
– это абсциссы точек
пересечения графиков функций
и
. Таким образом, очевидно, что таких точек
две.
Следовательно, нам подходит.
2) . Тогда уравнение примет вид
. Это уравнение имеет два решения
и
. Следовательно,
нам также подходит.
3) Пусть . Рассмотрим функцию
. Тогда
уравнение примет вид
.
Эта функция состоит из суммы двух функций: и
.
Функция
определена при всех
кроме
,
, причем на любом отрезке
принимает значения от
до
(вообще говоря, она еще периодическая).
Функция кубическая, определена при любом
, причем на каждом отрезке вида
она ограничена (то есть ее область значений на этом отрезке – от
до
).
Обе функции и
также непрерывны на любом отрезке
. Следовательно,
функция
также непрерывна на любом таком отрезке, а также принимает значения от
до
. Значит, на любом таком отрезке существует хотя бы одна точка, удовлетворяющая
уравнению
. В частности, это верно и для
. Следовательно, на любом отрезке вида
существует хотя бы одно решение уравнения
.
Так как таких отрезков бесконечное множество, то и решений у уравнения бесконечно.
Следовательно, любые
нам не подходят.
Таким образом, ответ .
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых уравнение
имеет на отрезке ровно один корень.
(Задача от подписчиков)
С помощью формулы уравнение перепишется в виде
Найдем производную:
Заметим, что при
1) . Тогда знаки производной будут такими:

Заметим также, что при
. Действительно,

Таким образом, левая часть графика не пересекает ось абсцисс. Следовательно, для того, чтобы функция пересекала отрезок
2) . Тогда функция принимает вид
3) . Тогда знаки производной будут такими:

Заметим, что в этом случае однозначно не определяется значение . Поэтому рассмотрим по
отдельности каждый случай.
3.1) . Тогда
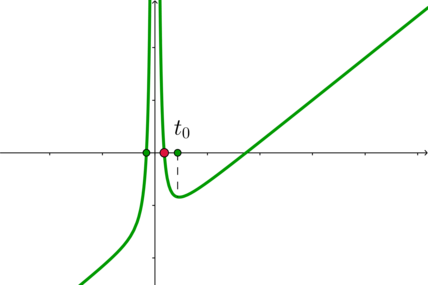
Заметим, что при
3.2) . График функции
в этом случае выглядит схематично
так:
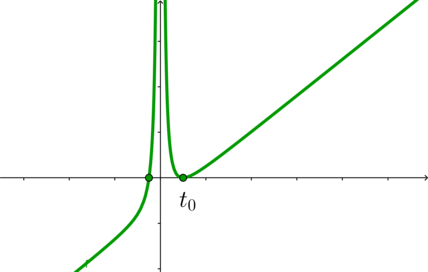
Заметим, что при
3.3) . График функции
в этом случае выглядит схематично
так:
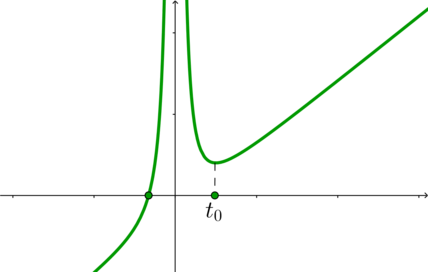
Следовательно, нужно:
Теперь вспомним, что все случаи 3.1, 3.2 и 3.3 мы рассматривали при . Следовательно, ответ
для 3 случая:
Тогда окончательный ответ в задаче:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет единственное решение.
Если , то
,
, следовательно,
только при
. Значит, при
оба синуса равны нулю,
следовательно, исходное равенство верно, то есть
при любом значении параметра является решением уравнения.
Заметим, что все остальные целые числа не являются решением уравнения, так как один синус зануляется, а второй —
нет.
Тогда требуется найти те , при которых других корней уравнение не имеет.
Пусть . Тогда уравнение стоит разделить на
, так как оно однородное:
Пусть . На промежутке
эта функция непрерывна, так как
, причем
- при
имеем
, следовательно,
;
- при
имеем
, следовательно,
.
Значит, . Тогда квадратное уравнение
не должно иметь корней, следовательно,



