Ошибка.
Попробуйте повторить позже
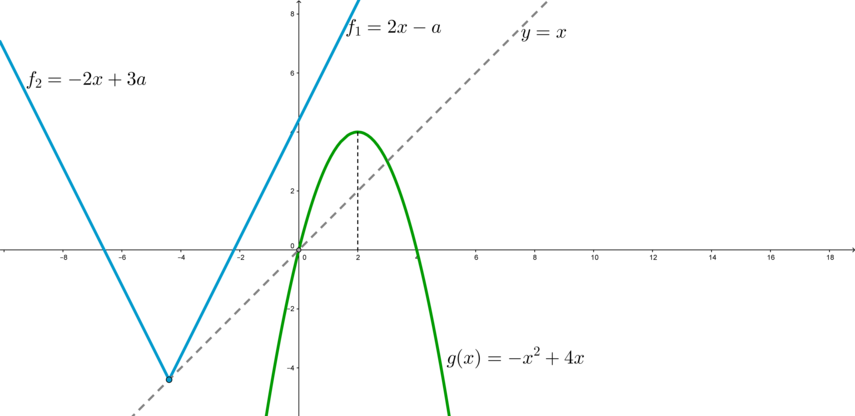
При каких значениях параметра уравнение
имеет ровно два решения?
В левой части имеем параболу Правой части соответствует семейство уголков модуля с вершинами на оси ординат, так
как координаты вершины
![]()
Рассмотрим случаи расположения уголка относительно параболы.
- В положении
вершина уголка совпадает с началом координат, то есть
и уголок имеет три точки пересечения с параболой. Этот случай нам не подходит.
- Если вершина уголка находится выше положения
уголок имеет ровно две точки пересечения с параболой: левая ветвь уголка с левой ветвью параболы и правая ветвь уголка с правой ветвью параболы. Этот случай нам подходит.
- Между положениями
и
каждая из ветвей уголка имеет ровно две точки пересечения с соответствующей ветвью параболы, суммарно четыре точки пересечения. Этот случай нам не подходит.
-
Если вершина уголка находится в положении
ветви уголка касаются параболы. Этот случай нам подходит, так как уголок имеет ровно две точки пересечения с параболой.
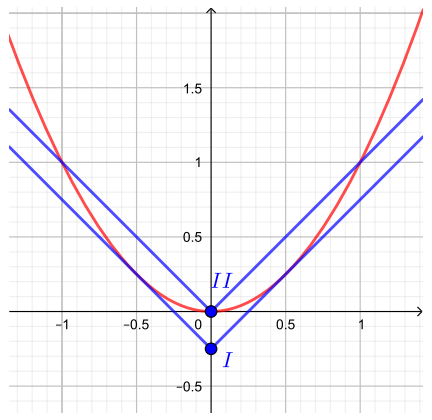
Найдем координаты вершины уголка в положении
В этом положении правая ветвь уголка, которая описывается уравнением
касается параболы, тогда из симметрии картинки и левая ветвь тоже касается. Запишем критерий касания функций
и
чтобы найти
- Если вершина уголка находится ниже положения
то уголок не имеет точек пересечения с параболой. Этот случай нам не подходит.
Объединяя все подходящие получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Ответ может отличаться от верного
включением | 3 |
| ИЛИ | |
| Недостаточное обоснование построения | |
| Рассмотрено верно одно из двух взаимных
расположений графиков функций, при
этом найдено хотя бы одно из ключевых
значений параметра | 2 |
| ИЛИ | |
| Значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
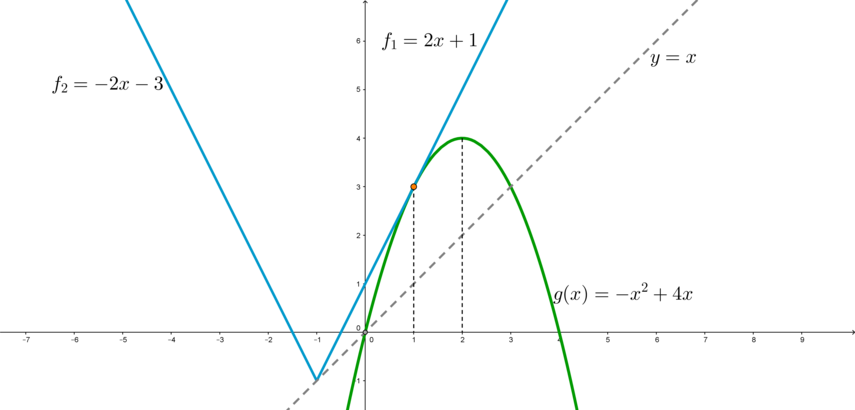
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Преобразуем исходное уравнение:
Правая часть задает пучок прямых через точку Графиком функции
является парабола
часть которой, лежащая ниже оси
отражена в верхнюю полуплоскость. Построим графики.
![]()
На картинке отмечены три ключевых положения прямых.
-
В положении
прямая пучка будет иметь единственное пересечение с графиком
в точке
Это положение нам подходит. Подставим точку
в уравнение прямой пучка, чтобы найти соответствующее значение
- В положении
имеем вертикальную прямую, которая не входит в пучок.
-
Любая прямая между положениями
и
будет иметь ровно две точки пересечения с графиком
Первая — пересечение с отраженным кусочком параболы, вторая — с левой веткой параболы. Эта точка пересечения будет существовать, так как квадратичная функция растет быстрее, чем линейная. Эти случаи нам не подходят.
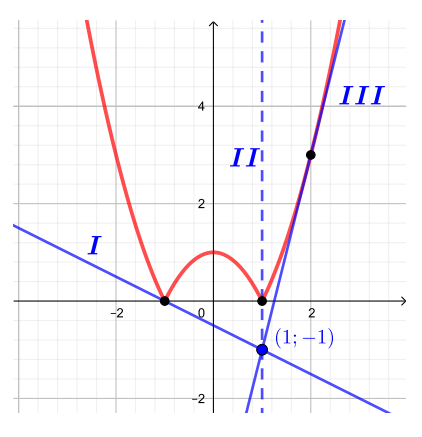
-
В положении
прямая пучка касается правой ветки параболы, то есть имеет с ней единственную точку пересечения. Найдем эту точку касания и значение
которое соответствует касательной.
Обозначим через
координату по оси абсцисс искомой точки касания. Тогда должны выполняться два условия. Во-первых, точка
должна принадлежать прямой
Во-вторых, производная функции
задающей на промежутке
правую ветку параболы, должна быть равна
в точке
так как это и есть наклон нашей касательной. Запишем эти условия с учетом
и
Условию
удовлетворяет только
следовательно,

- Между положениями
и
прямая пучка будет иметь два пересечения с правой веткой параболы, поскольку квадратичная функция растет быстрее, чем линейная, значит, такие положения нас не интересуют.
- Во всех оставшихся положениях точек пересечения не будет вовсе.
Резюмируя, получаем, что уравнение будет иметь единственное решение при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование построения | 3 |
| Рассмотрены верно два из трёх взаимных
расположений графиков функций, при
этом верно найдено хотя бы одно из
значений параметра | 2 |
| ИЛИ | |
| Значения параметра найдены верно, но нет обоснования их нахождения на основе взаимного расположения графиков функций | |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система
имеет хотя бы одно решение.
Систему можно переписать в виде:
График представляет собой параболу
, вершина которой сдвинута в точку
, то
есть движется по прямой
сверху вниз при увеличении
. Граничные положения параболы. при которых она
имеет хотя бы одну общую точку с лучом
,
, показаны на рисунке (параболы с вершинами в точках
и
):
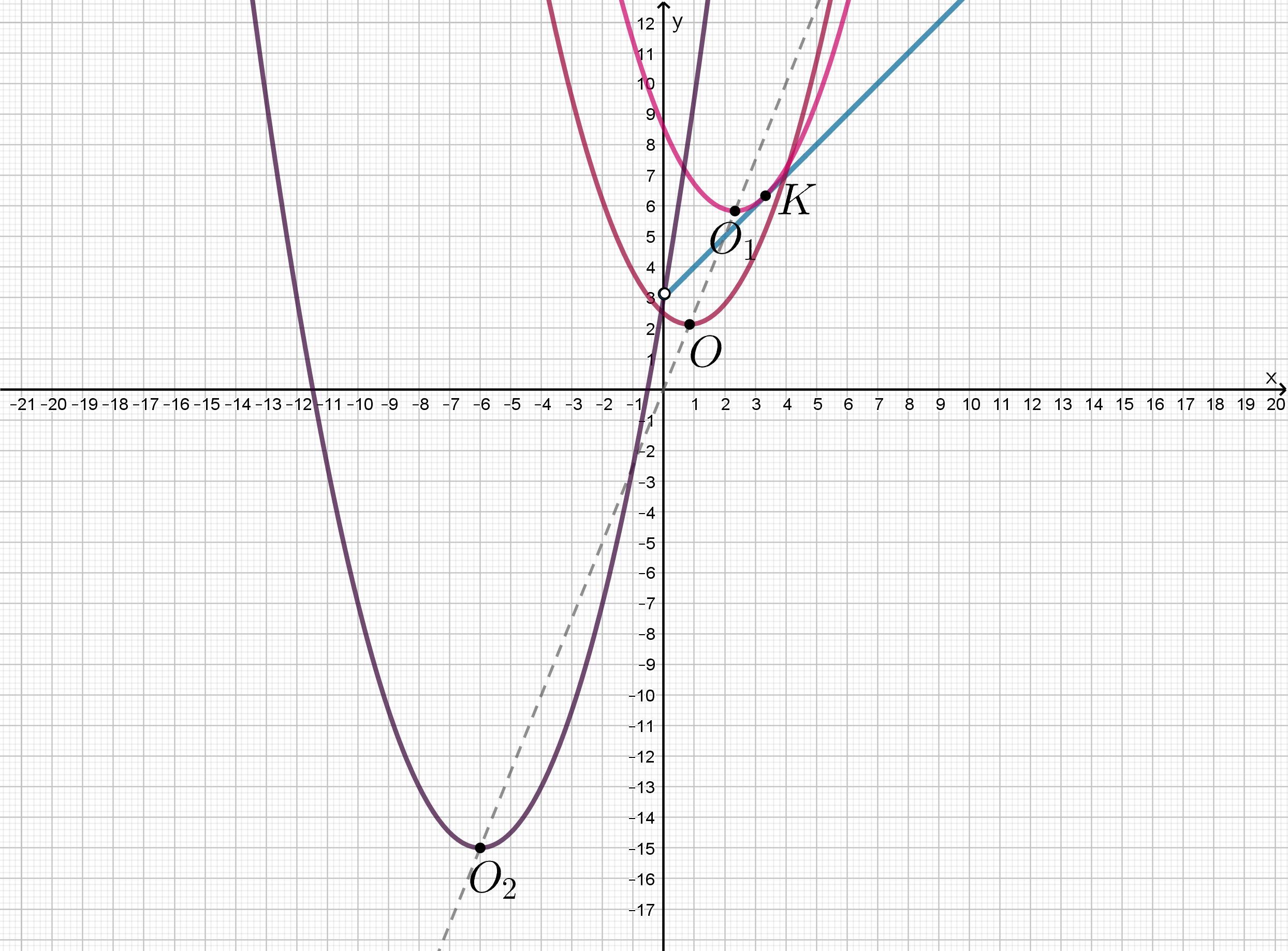
: парабола касается луча в точке
. Запишем условие касания
и
:
: парабола правой ветвью проходит через точку
:
Для правой ветви выбираем .
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите , при которых система
имеет ровно восемь решений.
Из второго уравнения следует, что . Если
, то решением второго уравнения являются две прямые
и
, решением
первого
. Три прямые не могут давать 8 точек пересечения, следовательно,
Тогда и график второго уравнения представляет собой две гиперболы
, график первого уравнения – две прямые
и
, опущенные вниз относительно прямой
, следовательно, эти две прямые должны иметь с двумя
гиперболами по четыре точки пересечения:
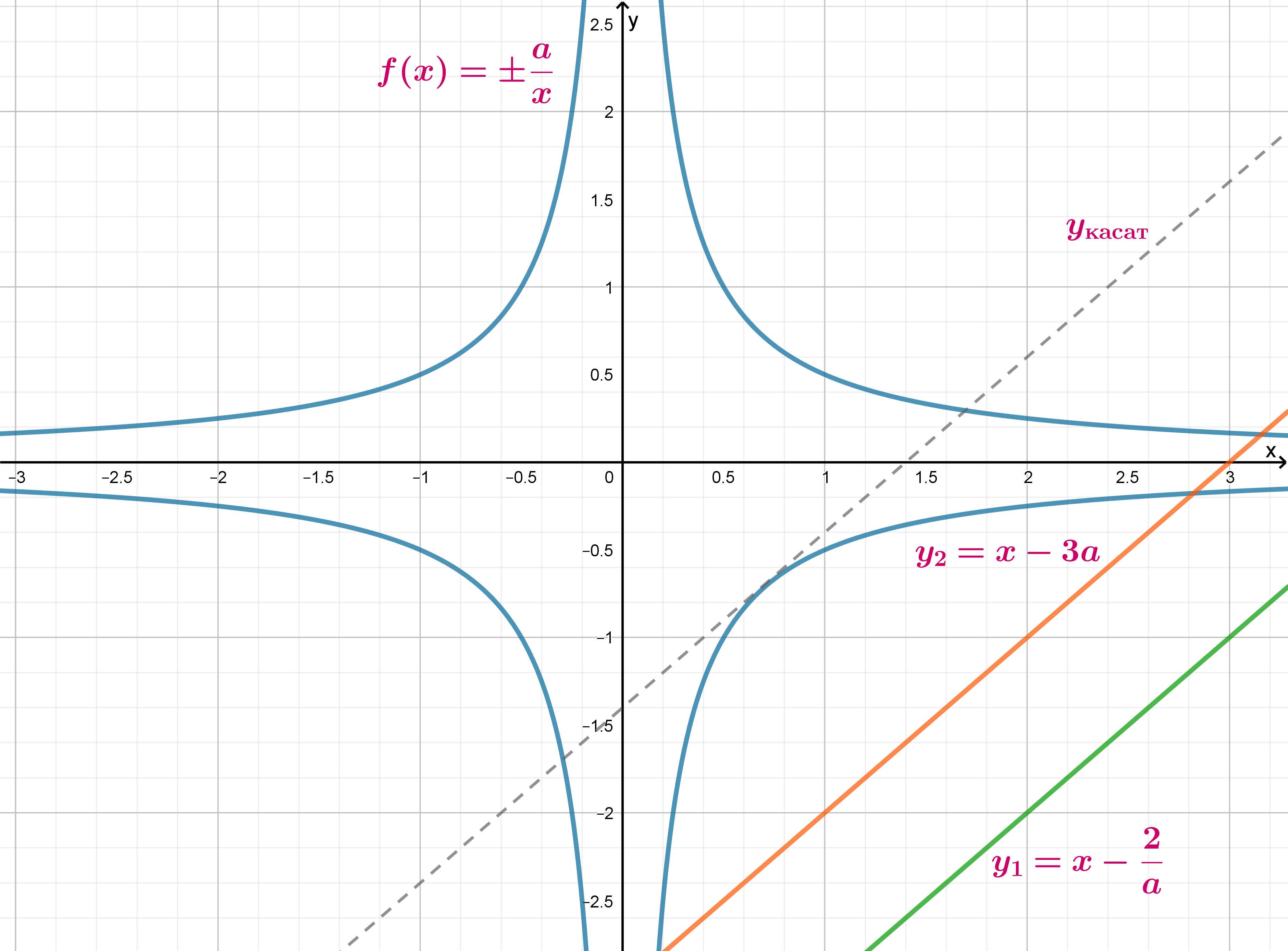
Подходящий вариант изображен на рисунке. Следовательно, нам нужно найти уравнение касательной к гиперболе в четвертой четверти, и тогда свободные коэффициенты наших прямых должны не совпадать и быть меньше, чем свободный коэффициент этой касательной.
Пусть , тогда
Следовательно, . Тогда
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых множеством решений неравенства
является отрезок.
Рассмотрим функцию , график которой строится в следующей последовательности:
Также рассмотрим функцию , график которой представляет собой уголок, ветви которого направлены вверх,а
вершина имеет координаты
, следовательно, движется по прямой
. При изменении
от
до
уголок движется слева направо. Построим графики и отметим те граничные положения уголка, между которыми уголок
находится в подходящем нам положении (то есть части уголка, находящейся не ниже корня, соответствует отрезок по
):
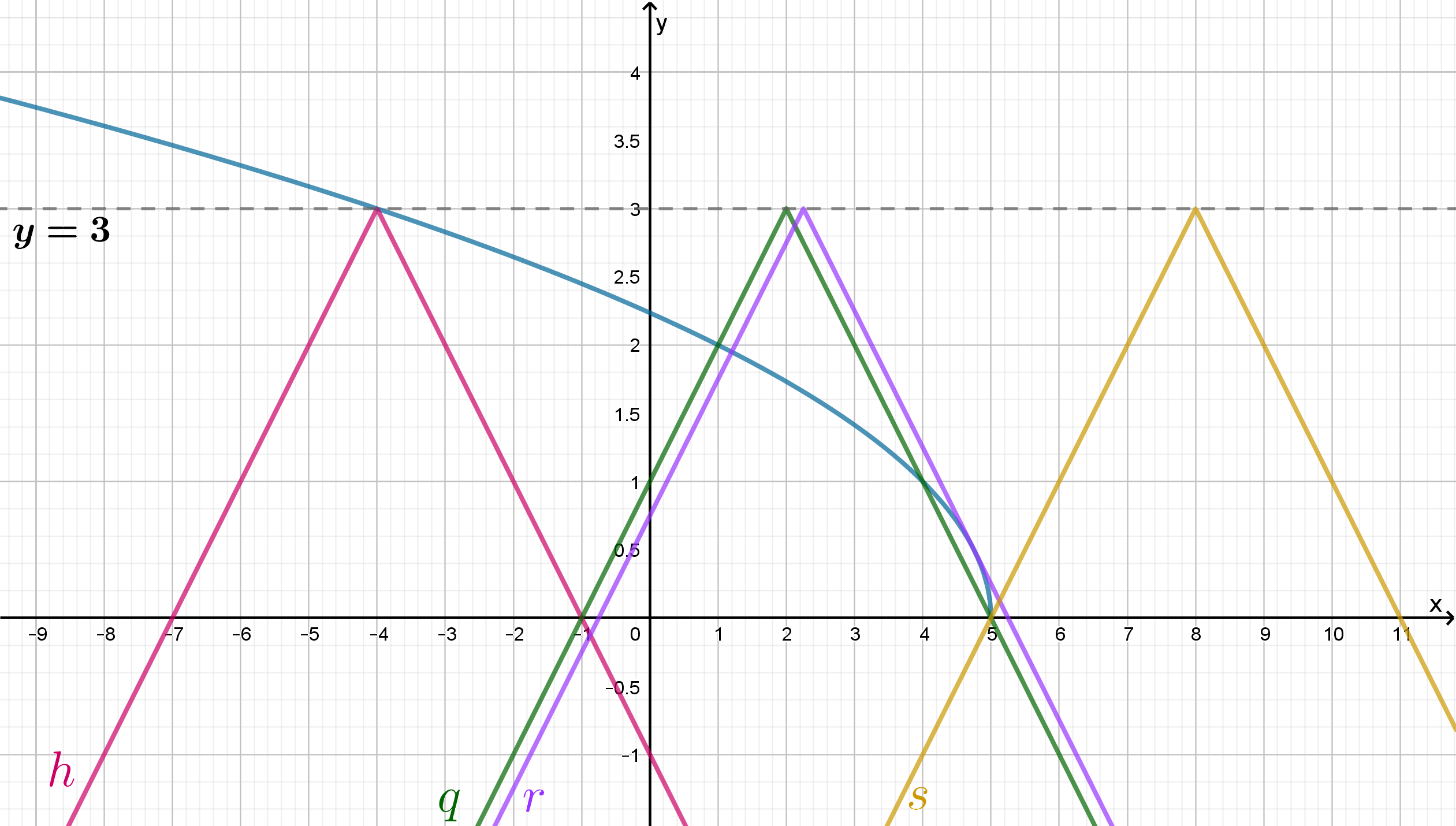
-
:
-
вершина уголка находится в точке пересечения корня и прямой
. Тогда решением неравенства является одна точка.
-
от
до
:
-
решением неравенства является отрезок.
-
:
-
правая ветка уголка проходит через точку
. Тогда решением неравенства является отрезок в объединении с одной точкой.
-
от
до
:
-
решением неравенства является объединение двух отрезков.
-
:
-
правая ветка уголка касается корня, тогда решением неравенства является объединение двух отрезков с совпадающим одним концом, то есть один отрезок.
-
от
до
:
-
решением неравенства яляется отрезок.
-
:
-
левая ветка уголка проходит через
, тогда решением неравенства яаляется одна точка.
Положение точка пересечения
и корня — это точка
, следовательно,
.
Положение правая ветка
проходит через
, следовательно,
, откуда
Положение
касается
Положение левая ветка
проходит через точку
, значит,
, откуда
.
Следовательно, ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых уравнение
имеет хотя бы один корень, и укажите число корней уравнения для каждого значения
Рассмотрим две функции и
Тогда уравнение примет вид
Следовательно, графики этих
функций должны иметь хотя бы одну точку пересечения.
Построим график с помощью следующей епочки преобразований:
График представляет собой пучок прямых, проходящих через точку
(то есть все виды таких прямых, кроме
вертикальной).
Изобразим положения прямой при которых есть решения:
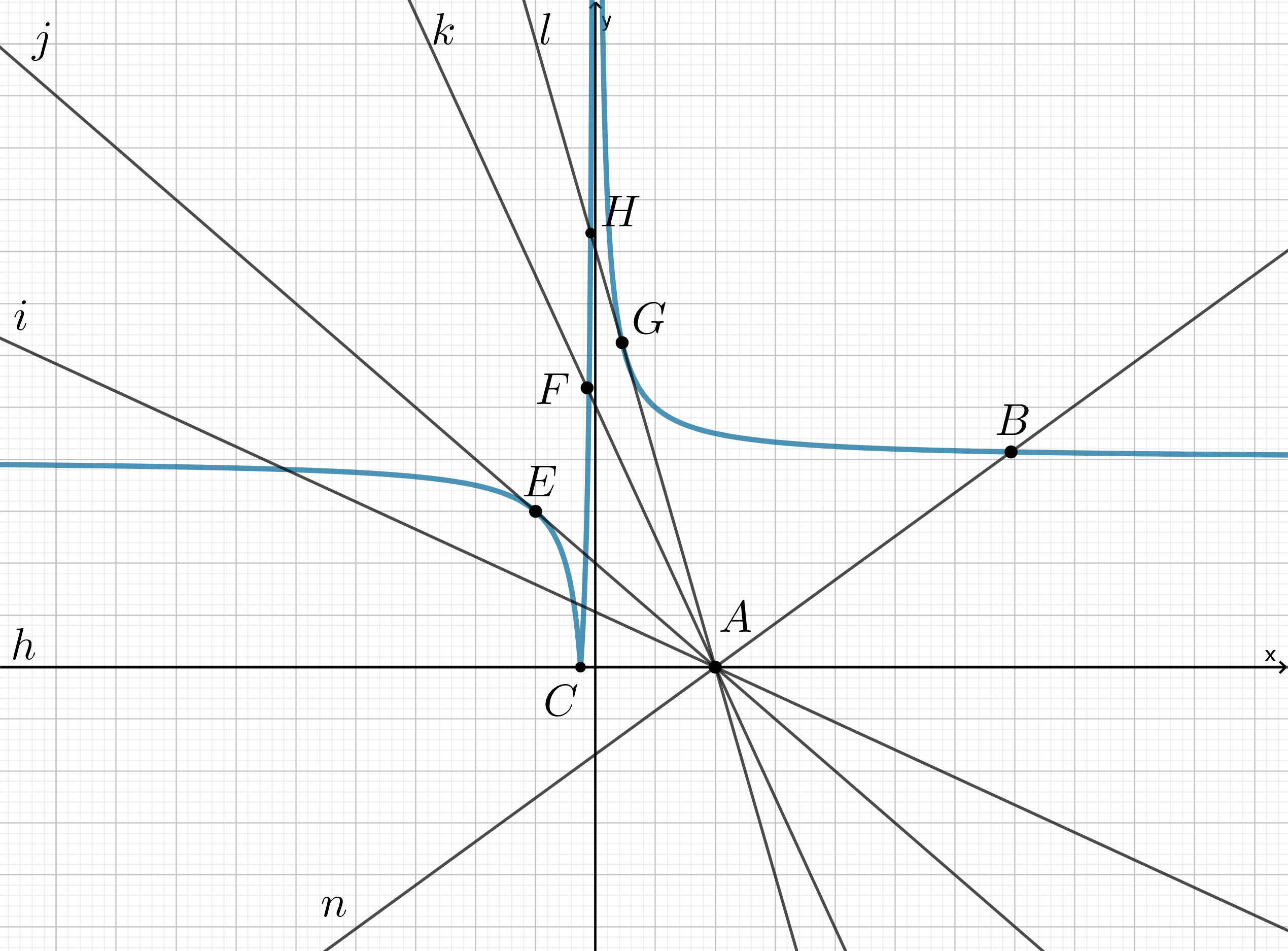
Пусть тогда
(назовем эту прямую
).
- 1.
- Меняя
от
до
получим одну точку пересечения прямой
с графиком
(например, положения
— точка
и
— точка
).
- 2.
- Меняя
от
до положения
имеем три точки пересечения, а в положении
— две (
и
).
- 3.
- Во всех положениях между
и
имеем одну точку пересечения (например, точка
в положении
).
- 4.
- В положении
(касание в точке
) имеем две точки пересечения.
- 5.
- В положениях между
и
имеем три точки пересечения.
Требуется найти
а
и
касание
и
Таким образом:
3 корня:
2 корня:
1 корень:
— 1 корень
— 2 корня
— 3 корня
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточно обоснованно построение или недостаточно обоснован какой-то момент при исследовании | 3 |
| Верно найдены граничное значение параметра, но есть ошибка в исследовании количества решений | 2 |
| ИЛИ | |
| допущена вычислительная ошибка | |
| Сведено к исследованию графически или аналитически и выполнено верное построение с обоснованием | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения при которых уравнение
имеет ровно три различных корня.
Рассмотрим следующие функции:
Тогда исходное уравнение имеет вид следовательно, необходимо, чтобы графики этих функций имели три точки
пересечения.
График (назовем его «птичка») строим последовательно так:
Вершина уголка — точка
следовательно, она движется по прямой
Граничные положения:
Положение 1. Точно: если левая ветвь уголка проходит через точку
Положение 2. Возможно: если вершина уголка находится в точке
Положение 3. Возможно: если левая ветвь уголка касается центра птички
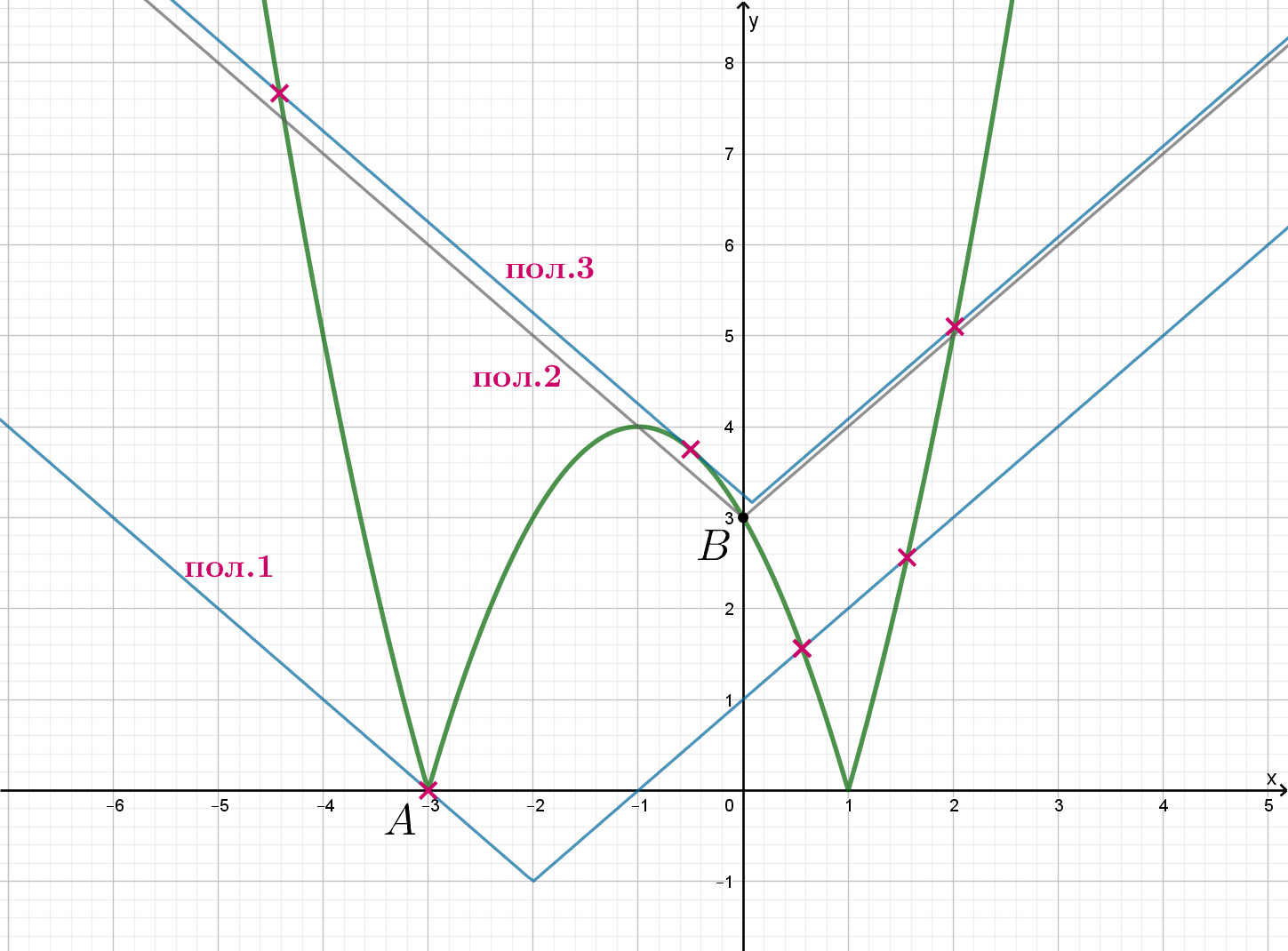
Исследуем эти три позиции. Левая ветвь уголка имеет вид
Положение 1.
Положение 2.
Тогда точно есть две точки пересечения с ветвями птички, одна с центром птички. Значит, надо проверить, есть ли еще точки пересечения с центром птички:
Таким образом, точек пересечения четыре, значит, это положение нам не подходит. Двигая уголок выше, мы получаем также четыре точки пересечения вплоть до касания (положение 3).
Положение 3. Запишем условие касания и
Двигая уголок выше, мы получаем две точки пересечения.
Значит, исходное уравнение имеет ровно три различных корня при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены верные значения параметра, но есть недостаток в обосновании | 3 |
| Верно исследован случай касания или верно рассмотрены два других положения | 2 |
| Обоснованно сведено к исследованию графически или аналитически | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет ровно два решения.
Система равносильна уравнению , где
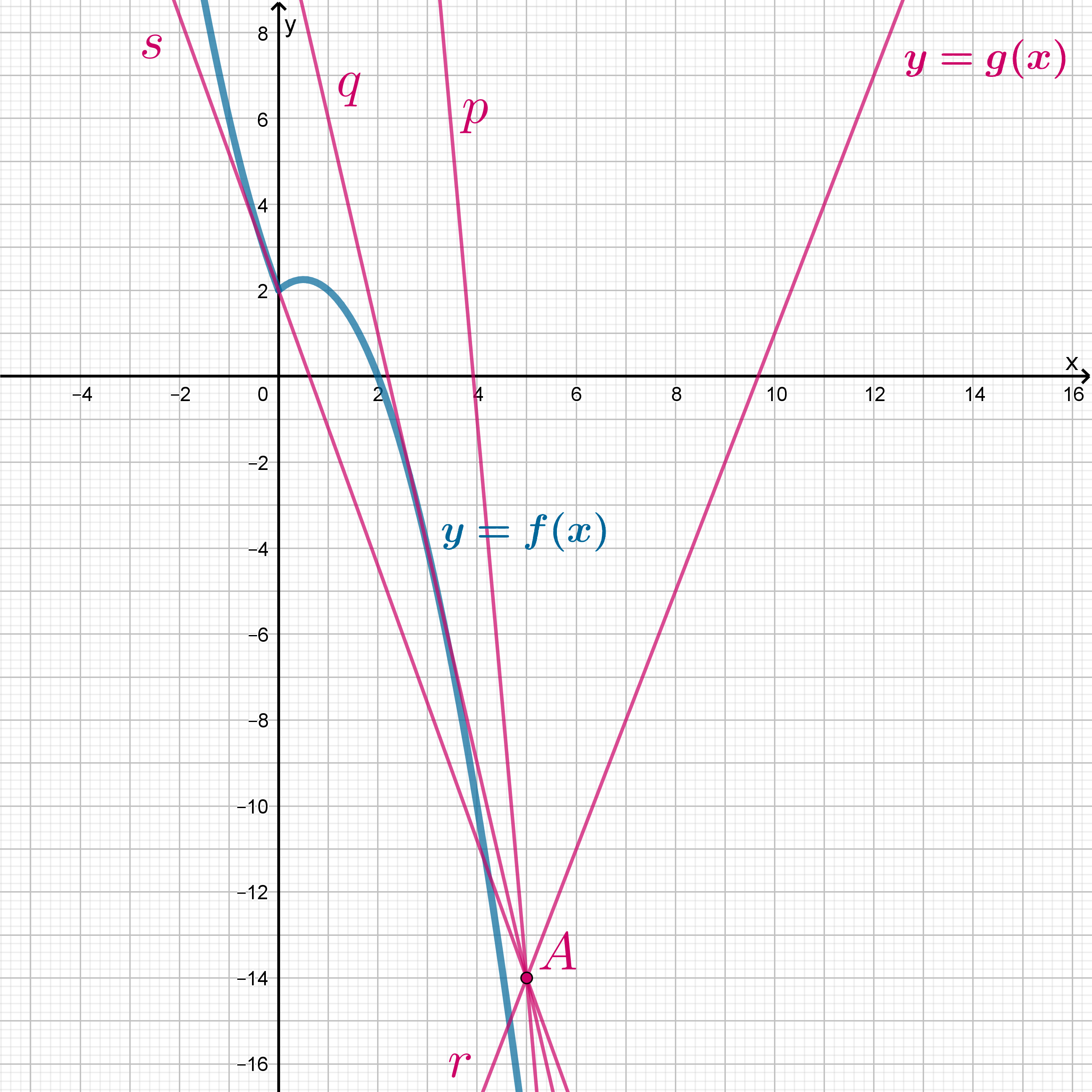
График состоит из двух частей двух парабол. Графиком
является пучок прямых, проходящих через точку
. Заметим, что при
имеем
. Система будет иметь два решения тогда и только тогда, когда прямая
будет иметь две точки пересечения с графиком
. Известно, что произвольная прямая может иметь 0, 1 или 2 точки
пересечения с параболой.
Из наших графиков следует, что при прямая
имеет ровно одну общую точку с графиком
(положение
), так как
прямая имеет “положительный наклон” к оси абсцисс или является горизонтальной.
Пусть . Рассмотрим следующие ситуации: прямая касается графика
или
:
1) касается
(положение
или
):
Что можно сказать по поводу числа общих точек и
: при
имеем 2 точки, при
и
– по 1
точке, при
– 0 точек.
2) касается
(положение
):
Что можно сказать по поводу числа общих точек и
:
при
– 3 точки,
при
– 2 точки,
при
– 1 точка,
при
– 2 точки,
при
– 3 точки,
при
– 2 точки,
при
– 1 точка.
Следовательно, система имеет 2 решения при .
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых система уравнений
имеет больше трех решений.
Преобразуем первое равенство. Так как равносильно
при
, то
Графиком полученной системы является объединение частей гиперболы и прямой
, лежащие в области под
гиперболой
Преобразуем второе равенство. Будем рассматривать его как квадратное относительно переменной :
Его дискриминант равен
Следовательно, решения
Графиком полученной совокупности является объединение двух прямых, одна фиксирована — это , а
представляет
собой пучок прямых, проходящих через точку
Изобразим все графики на одной координатной плоскости и определим положения, которые может занимать прямая
, чтобы имелось более трех точек пересечения. Голубым цветом обозначена область, задающаяся неравенством
, зеленым цветом обозначены графики функций
и
, а розовым — прямые
и
.
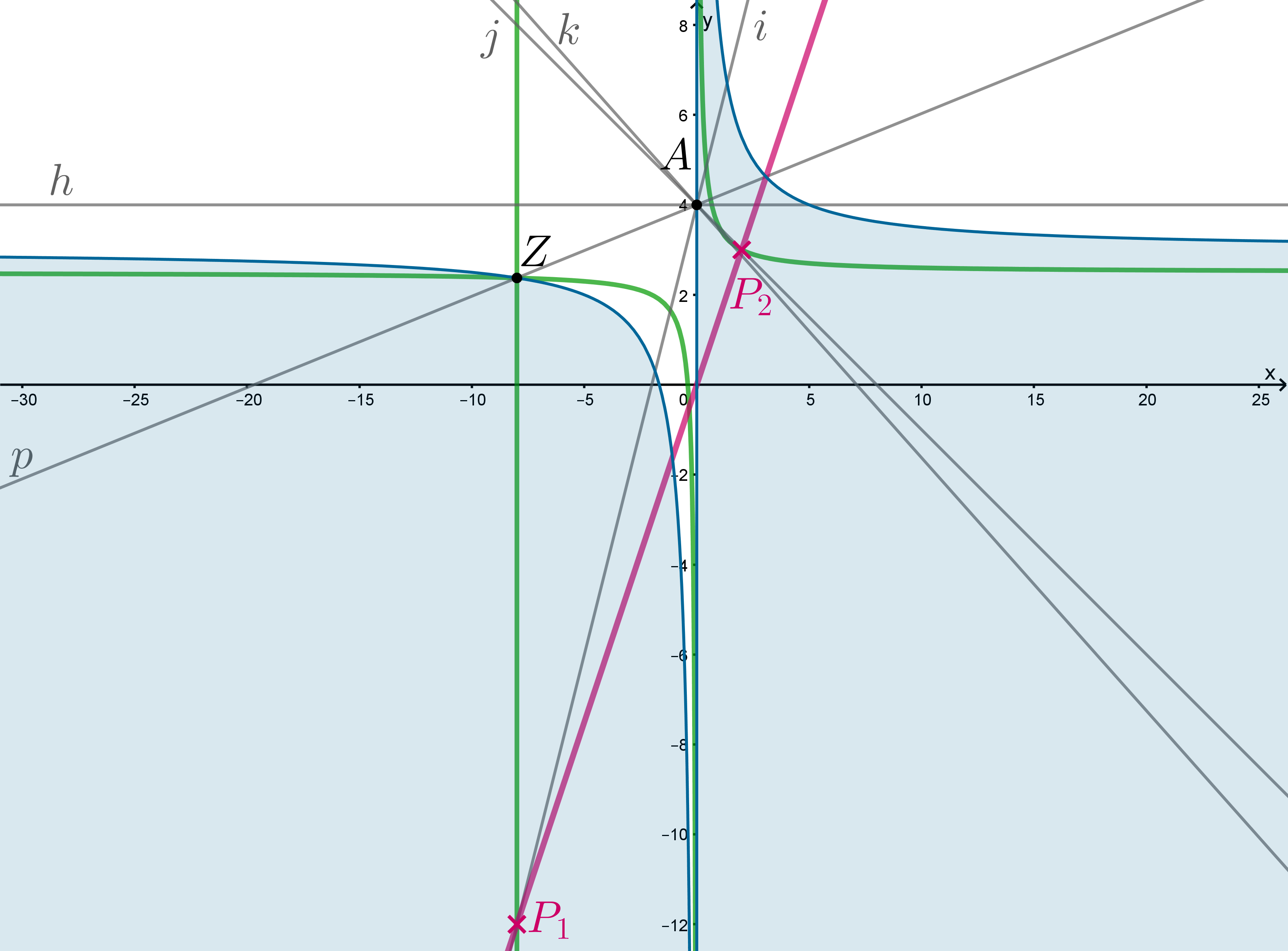
Заметим, что точка пересечения
и
лежит на гиперболе
.
Также заметим, что две точки пересечения и
имеются всегда: их дает прямая
. Значит, нужно, чтобы прямая
давала как минимум две точки пересечения.
-
Рассмотрим
и будем вращать прямую
(назовем ее
) от
до
. Прямая
соответствует
и в этом положении
дает одну точку (не подходит). При увеличении
прямая
дает две точки пересечения (одну в правой полуплоскости, вторую – в левой, обе с
), и так происходит до тех пор, пока
не окажется в положении прямой
(пройдет через точку
). Вращая далее, прямая
будет также давать две точки пересечения, но в левой полуплоскости эта точка будет уже на прямой
. И так вплоть до положения прямой
, когда эта точка пересечения совпадет с точкой
(не подходит). вращая далее вплоть до
прямая
будет продолжать давать две точки пересечения, что нам подходит.
Следовательно,
,
. Как мы уже сказали,
, найдем
.
Точка
— точка пересечения прямых
и
, следовательно,
. Подставим координаты этой точки в уравнение
:
Значит.
. Таким образом,
-
Рассмотрим
. Будем вращать прямую
в обратном направлении от
до
. Вплоть до положения прямой
(проходит через точку
) прямая
дает две точки пересечения, положение
нам не подходит. Вращая далее, мы получаем две точки пересечения (все так же в правой полуплоскости), пока
не окажется в положении
(коснется гиперболы в правой полплоскости). Это положение и все последующие нам уже не подходят. Следовательно,
.
точка
— точка пересечения прямой
и гиперболы
:
Подставим координаты точки
в уравнение
:
Теперь найдем
: когда прямая
касается
в точке
:
Значит,
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно три различных решения.
График функции получается из графика функции
отражением относительно оси ординат, а затем отражением той
части графика, что находится ниже оси абсцисс, наверх. График
представляет собой пучок прямых, проходящих через начало
координат.
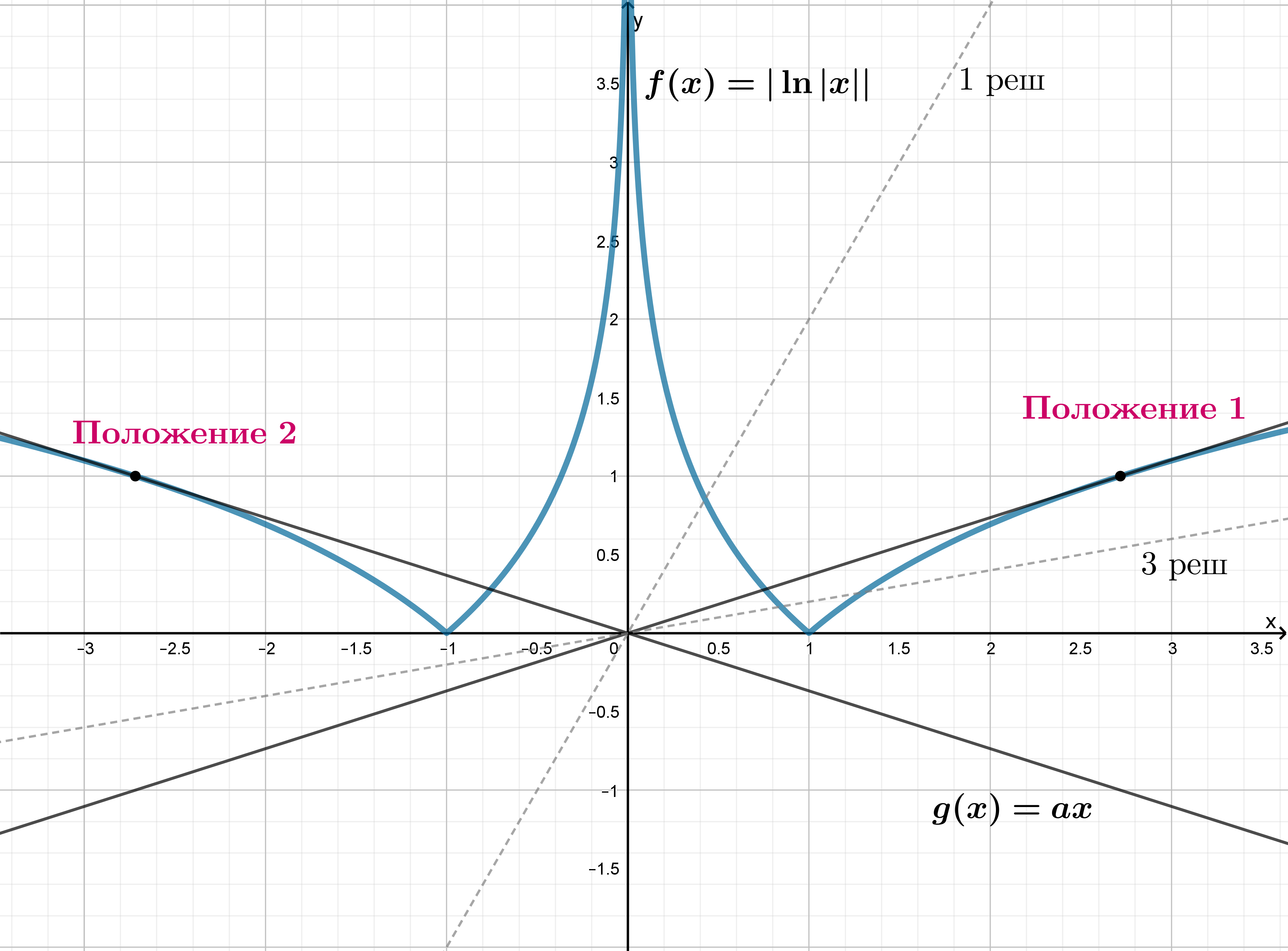
Следовательно, если и вращать прямую
от
до
, то до Положения 1 графики будут иметь 3 точки
пересечения, в Положении 1 — две точки пересечения, далее — одну. Следовательно, найдем значения параметра в Положении 1, то есть
положение, при котором прямая
касается графика функции
. Для этого запишем систему, задающую условие
касания:
В силу симметрии графиков и
относительно оси ординат, Положение 2 задается значением параметра
.
Следовательно, подходящие значения параметра
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых система уравнений
|
|
имеет единственное решение.
Рассмотрим систему внимательнее и преобразуем её условия:
|
|
|
|
|
|
|
|
Получили полуокружность и пучок прямых, проходящих через точку .
Перейдём на координатную плоскость
:
1 случай:
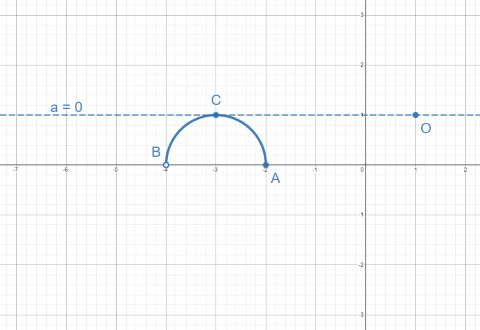
При прямая
становится параллельной оси абсцисс и
проходит ровно через одну точку
полуокружности. Иными словами,
касается полуокружности – такой случай нам подходит и
– часть
ответа.
2 случай:
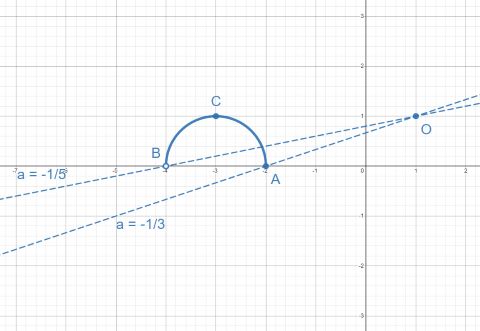
Когда прямая
пересекает полуокружность ровно в
одной точке. Иными словами, мы берём в ответ все прямые, лежащие между
прямыми
и
, включая
и исключая
.
пересекает
полуокружность уже в двух точках.
Вычисления ключевых значений параметра:
Прямая (проходит через точку
):
Прямая (проходит через точку
):
Прямая (проходит через точку
):
.
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| С помощью верного рассуждения получены все верные значения параметра, но решение недостаточно обосновано | 3 |
| ИЛИ | |
| в ответ включена точка | |
| ИЛИ | |
| потеряна точка | |
| ИЛИ | |
| потеряна точка | |
| С помощью верного рассуждения получен неверный ответ из-за вычислительной ошибки, при этом верно выполнены все шаги решения | 2 |
| ИЛИ | |
| полученный
ответ отличается от правильного
включением/исключением двух или
трёх точек из набора | |
| В случае аналитического решения
найдено значение | 1 |
| ИЛИ | |
| в случае графического решения: задача верно сведена к исследованию взаимного расположения линий (изображены необходимые фигуры, учтены ограничения, указана связь исходной задачи с построенными фигурами) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых наибольшее значение функции
не меньше
Для того, чтобы наибольшее значение функции было не меньше , нужно, чтобы у неравенства
было хотя бы одно решение. Рассмотрим неравенство в виде
Графиком является уголок, вершина которого движется по оси абсцисс. Графиком
является
парабола, вершина которой находится в точке
. Требуется, чтобы существовала хотя бы одна точка уголка,
находящаяся либо на параболе, либо выше.
Граничные случаи показаны на рисунке. Причем заметим, что в силу симметрии параболы относительно оси и
симметрии уголка относительно прямой
эти случаи также симметричны относительно оси
, то есть если
положение 1 (левый уголок) достигается при
, то положение 2 (правый уголок) достигается при
.
Положение 1 выполняется, когда правая ветвь уголка касается параболы. Запишем условие касания
прямой и параболы, которое задается системой из двух равенств: равенства производных и равенства функций в точке
касания.
В силу описанной выше симметрии положение 2 достигается при
Тогда нам подходят все положения уголка левее положения 1 и правее положения 2, что задается значениями параметра
Ошибка.
Попробуйте повторить позже
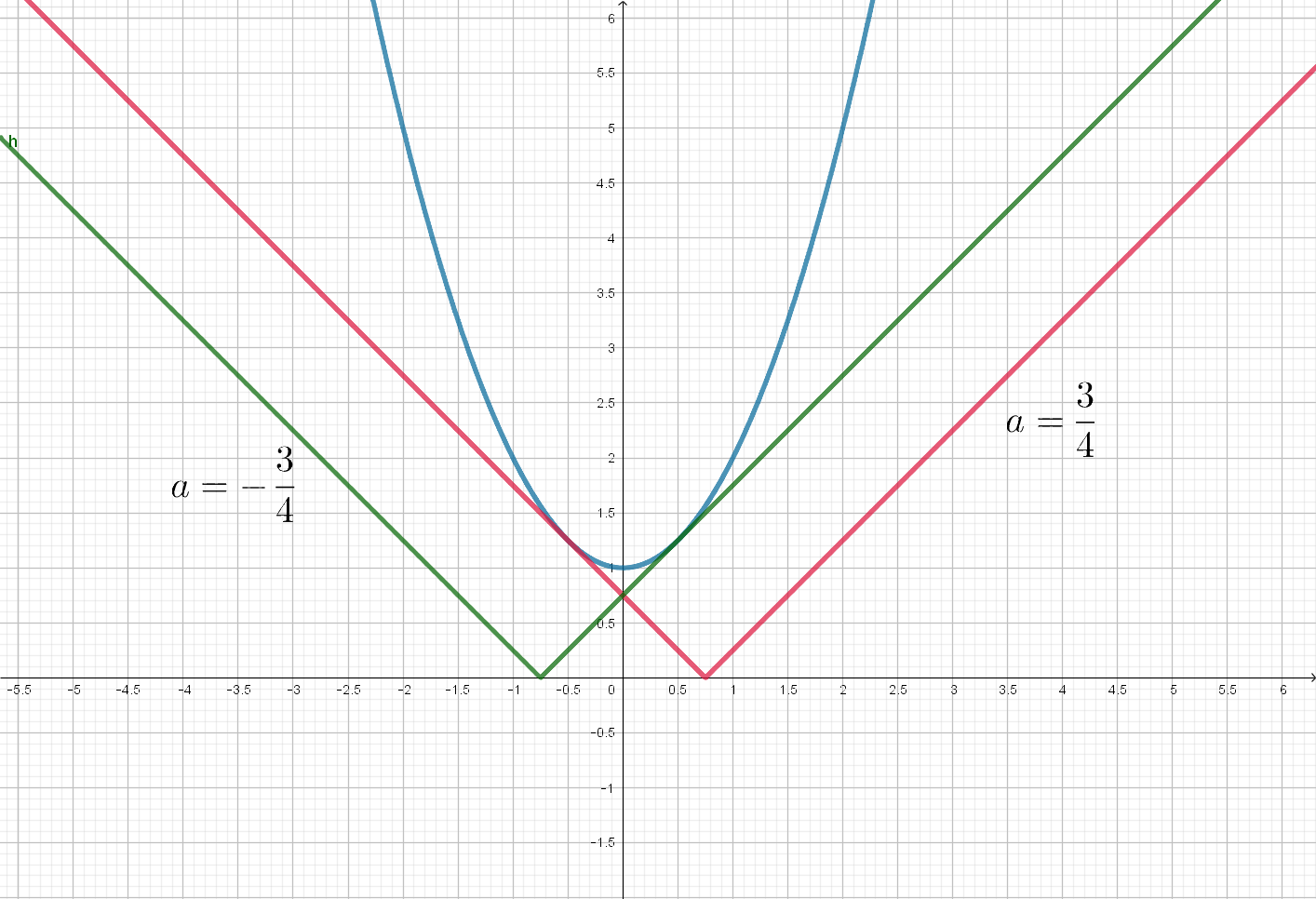
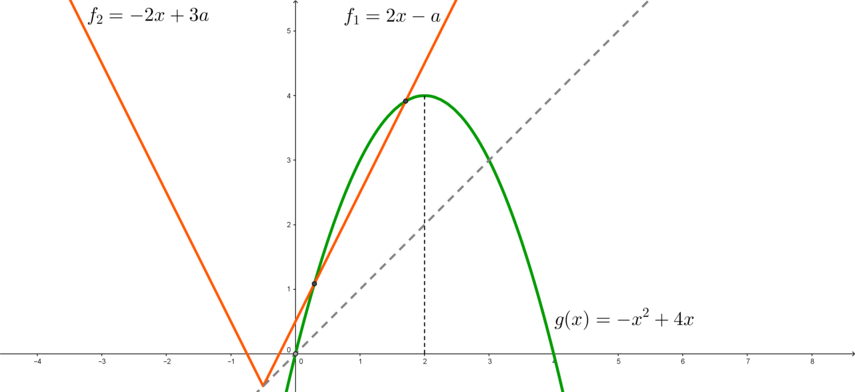
Найдите все возможные значения параметров и
, при которых уравнение
имеет ровно три различных корня, причем сумма каких-то двух из них равна нулю.
Перепишем уравнение в виде
Точка, в которой парабола пересекает
Заметим, что если вершина уголка находится выше этой точки (то есть
1) Рассмотрим случай, когда . Тогда
.
Заметим, что если ветви уголка направлены вниз (то есть ), а также при
,
не будет
пересекать
в трех точках.
Рассмотрим случай . Тогда мы имеем еще две точки пересечения
с
: точки
и
.
Так как точка находится левее
(абсцисса вершины параболы), то
.
Следовательно, и
. Значит, не может быть
, следовательно, только
,
откуда
. Следовательно,
, то есть
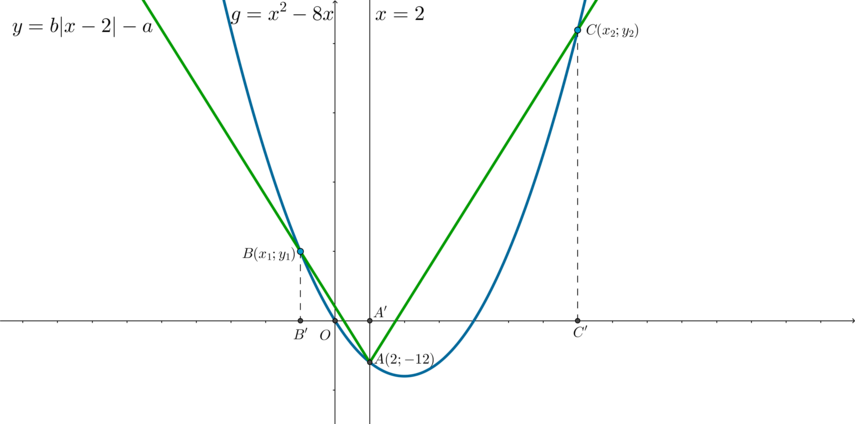
2) Рассмотрим случай, когда , то есть
.
Заметим также, что если , то
не будет иметь 3 точки пересечения с
. Следовательно,
рассматриваем только случай, когда ветви уголка направлены вверх.
будет иметь 3 точки пересечения с
в одном из двух случаев:
— когда левая ветка уголка касается параболы, а правая пересекает в двух точках (см. второй
рисунок);
— когда левая ветка уголка пересекает параболу в двух точках, а правая касается.
a) Рассмотрим первый случай.
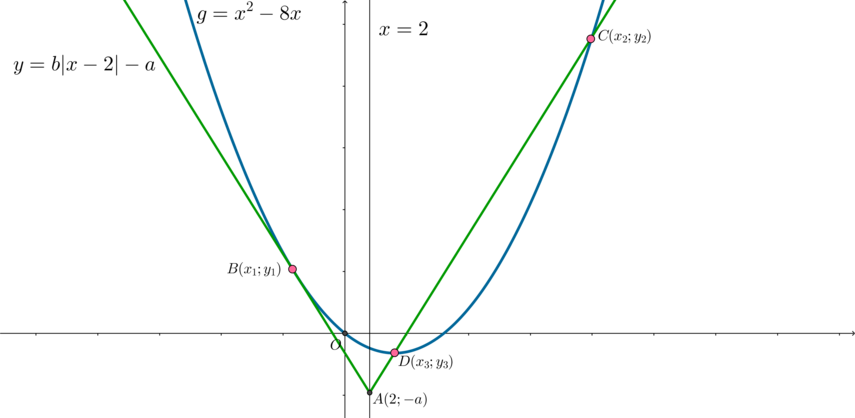
Левая ветка уголка задается уравнением ,
. Следовательно, условие
касания:
Таким образом, получен еще один ответ
b) Рассмотрим второй случай.
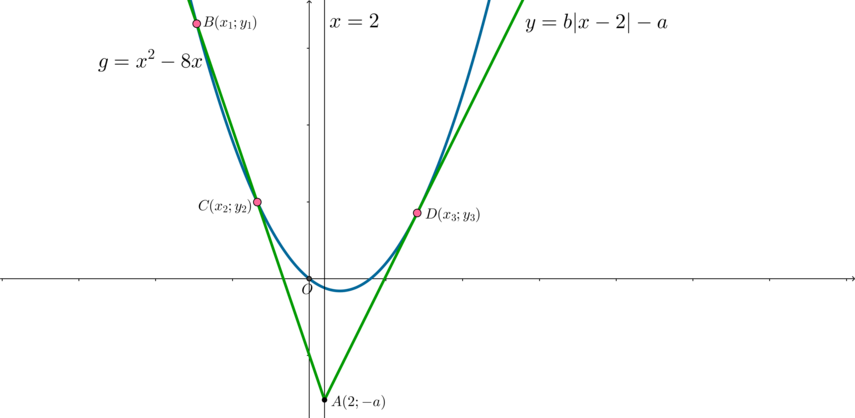
Аналогично получаем систему:
и
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых неравенство
Перепишем неравенство в виде:
Пусть ,
– функции. Тогда по условию задачи необходимо,
чтобы промежуток, для которого график
лежит не выше графика
, содержал ровно одну целую
точку.
Заметим, что графиком функции является уголок, вершина которого скользит по прямой
.
Правая ветвь уголка задается уравнением
при
; левая ветвь —
при
.
1) Найдем значение параметра, при котором правая ветвь уголка касается параболы (т.к. если уголок
находится левее этого положения, то неравенство не имеет решений).. Если
касается
в точке
, то
равно коэффициенту при
в уравнении
, то есть:
Т.к. касается
, то
, откуда находим значение параметра
.
Таким образом, при правая ветвь
касается параболы:
Заметим, что при существует ровно одно решение для неравенства, и это
, что
является целочисленным значением. Следовательно,
нам подходит.
2) Заметим, что при вершина уголка находится в точке
и уголок имеет две точки
пересечения с параболой:
и
. Следовательно, решением неравенства является отрезок
(т.к. на этом отрезке уголок находится не выше параболы), содержащий три целых точки (
и
). А вот при
(но
) левая ветвь уголка не пересекает параболу, а правая ветвь
пересекает параболу в двух точках, причем одна находится между
и
, а вторая между
и
. То
есть в промежуток, удовлетворяющий неравенству, будет входить ровно одна целая точка
.
Следовательно, все
нам подходят.
3) Заметим, что если вершина уголка находится в точке (то есть
), то левая ветвь
уголка касается параболы (в этой точке). Действительно, это можно проверить, поступив так же, как
мы поступили в первом пункте:
. Если
касается
в точке
, то
равно
коэффициенту при
в уравнении
, то есть:
Следовательно, при решением неравенства является единственная точка
, которая
является целой, то есть
нам подходит.
Заметим также, что при уголок будет находится всегда выше параболы, то есть неравенство
не будет иметь решений.
4) Рассмотрим ситуацию, когда . При этих
правая ветвь уголка пересекает параболу в
точке
, а вот левая ветвь пересекает параболу в какой-то точке
. Следовательно,
чтобы неравенство имело единственное целочисленное решение, этим решением должно быть
и
точка
, в которой левая ветвь пересекает параболу, должна удовлетворять:
(оранжевый
уголок).
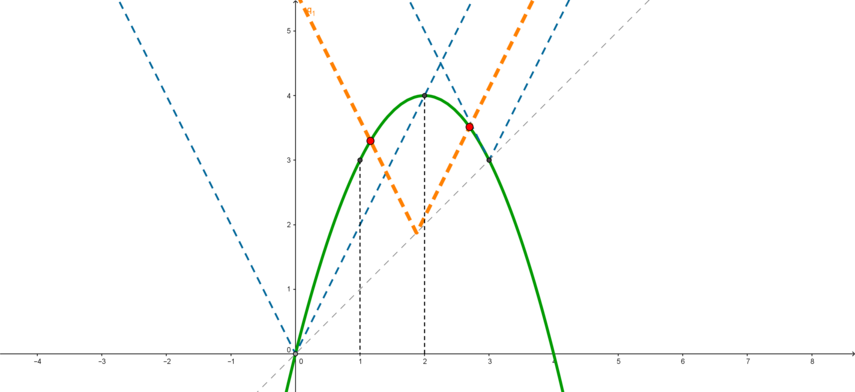
Поэтому найдем значение , при котором левая ветвь уголка пересекает параболу в точке
:
Теперь найдем значение , при котором левая ветвь уголка пересекает параболу в точке
:
То есть при решением неравенства является отрезок
, содержащий 2 целые точки
(
); при
решением неравенства является отрезок
, содержащий одну целую точку
(
).
Следовательно, при решением будет отрезок
, который содержит одну целую
точку
. Такие значения
нам подходят.
Таким образом, итоговый ответ:
при целочисленное решение
;
при целочисленное решение
;
при целочисленное решение
.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых графики уравнений
имеют ровно одну общую точку.
Графиком уравнения является парабола, пересекающая ось
в точках
и
а ось
в точке
Графиком уравнения при каждом фиксированном
является прямая.
1) При это прямая
имеющая ровно одну точку пересечения с параболой, а именно точку
Этот случай нам
подходит.
2) При это пучок прямых
проходящих через точку
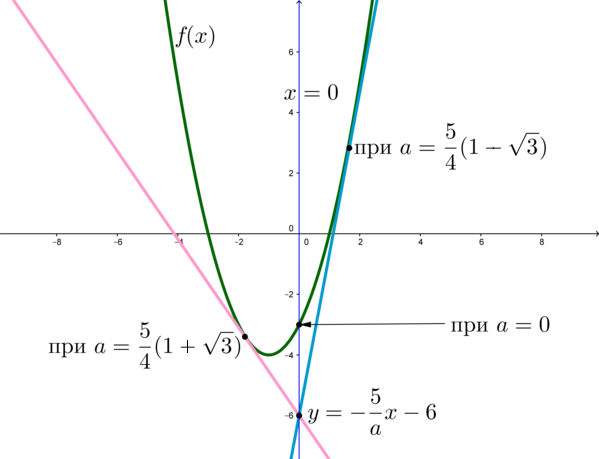
Графики имеют ровно одну общую точку при тех значениях при которых прямая
касается параболы. Запишем
условие касания параболы и прямой пучка:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Ответ отличается от верного
невключением | 3 |
| ИЛИ | |
| Недостаточное обоснование построения | |
| Рассмотрено верно одно из двух взаимных
расположений графиков функций ( | 2 |
| Верно сведено к исследованию графически или аналитически, при этом построение обосновано | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
При каких значениях уравнение
имеет ровно 2 корня?
Рассмотрим функции и
. Тогда уравнение примет
вид:
1) Заметим, что графиком при каждом фиксированном
является уголок, вершина которого
находится на прямой
.
Найдем , при котором левая ветка уголка будет касаться графика
в точке
. Тогда при всех
,
больших найденного значения, графики будут иметь ровно 2 точки пересечения.
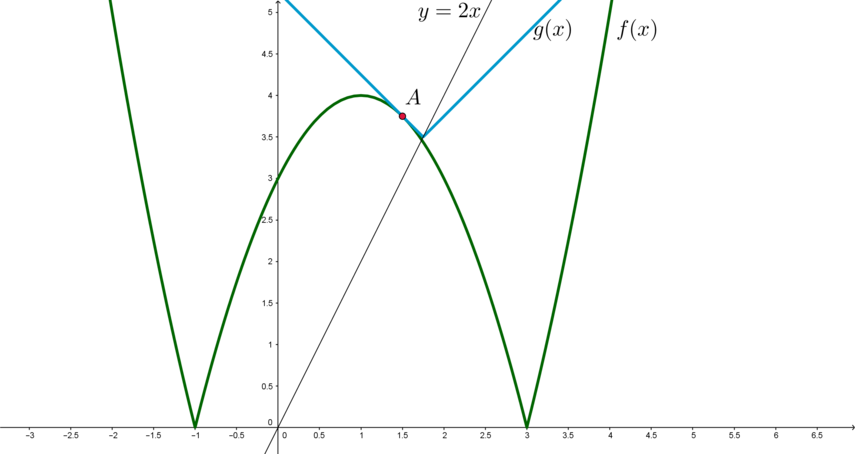
Левая ветка уголка задается уравнением ,
. Касаться она будет
графика функции
.
. Если
– точка касания, то
2) Найдем значения , когда
проходит через точку
(положение
) и через точку
(положение
).
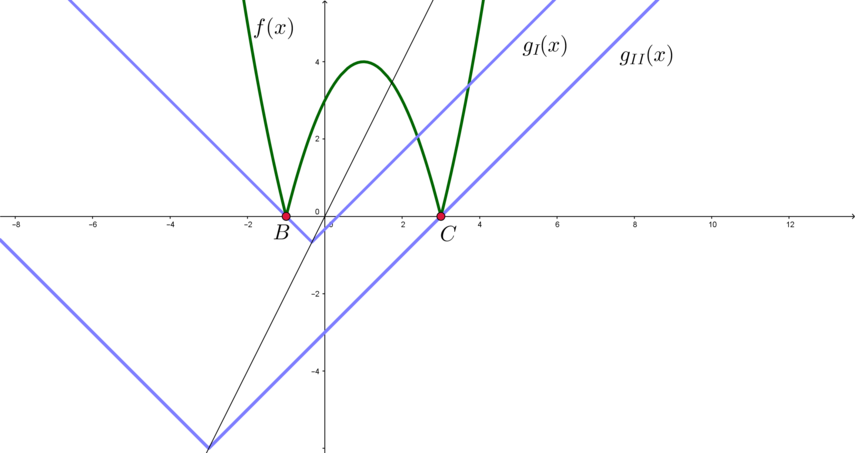
Заметим, что если находится между положениями
и
, то она имеет с
также ровно 2 точки
пересечения.
Для положения (левая ветка уголка проходит через
):
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых наименьшее значение функции
больше, чем .
Вопрос можно переформулировать следующим образом: неравенство
Перепишем неравенство в виде
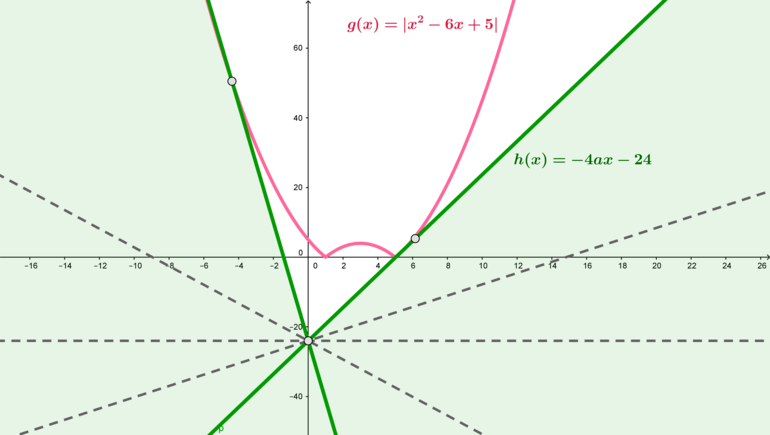
1) Рассмотрим случай, когда . Пусть прямая
касается правой ветви параболы
(при
).
. Следовательно, если они касаются в точке с абсциссой
, то
Следовательно, при
Тогда при всех
2) Рассмотрим случай, когда . Тогда прямая
параллельна оси абсцисс и находится
ниже графика
при всех
. Следовательно, это значение
нам подходит.
3) Рассмотрим случай, когда . Пусть прямая
касается левой ветви параболы
(при
).
. Следовательно, если они касаются в точке с абсциссой
, то
Следовательно, при всех
Итого заключаем, что нам подходят значения:
Прямые должны находиться в зеленой области.
Ошибка.
Попробуйте повторить позже
Найдите все возможные значения параметра , при каждом из которых уравнение
имеет ровно одно решение.
Рассмотрим функцию и пучок прямых
.
– точка максимума,
– точка минимума.
.
Все прямые проходят через точку
.
Найдем случаи, когда прямая касается графика функции
(
– точка касания). Найдем
соответствующие этому значения параметра:
Таким образом, уравнение будет иметь единственное значение при тех значениях
, при
которых прямые
будут располагаться в закрашенных областях: (причем граничный случай
не подходит)
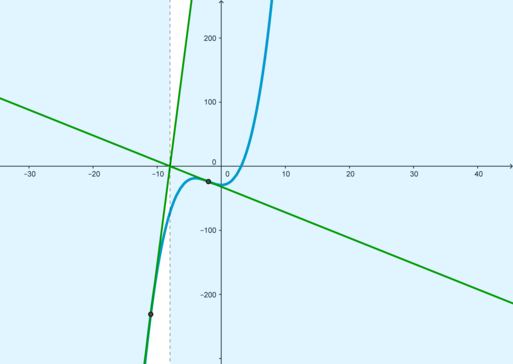
В уменьшенном масштабе это выглядит так:
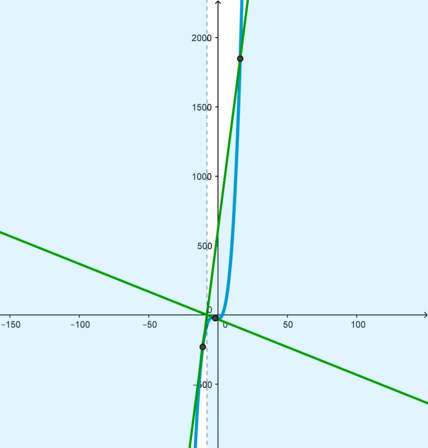
Следовательно, .
.
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет
единственное решение.
Пусть . Рассмотрим несколько случаев:
1) . Тогда уравнение имеет единственное решение
.
2) . Найдем производную
. Т.к.
, то
при любых
. Следовательно,
функция
монотонно возрастает на всем
. Значит, имеет не более одной точки пересечения с осью
.
Заметим, что , следовательно, на промежутке
есть точка
, в которой
. Значит,
и есть единственное решение данного
уравнения.
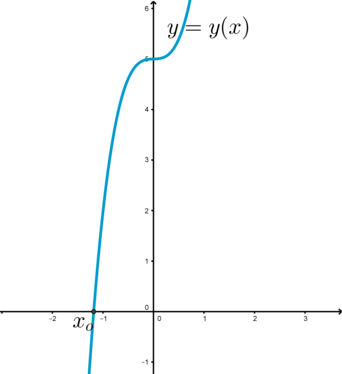
3) . Обозначим
.
Рассмотрим уравнение в виде . Обозначим
. Найдем
положительные значения
, при которых функции
и
имеют ровно одну точку
пересечения.
Найдем значения , при которых
касается
:
. Пусть
– точка касания. Тогда:
Значит, при функции
и
имеют 2 точки пересечения, а при
функции
и
имеют ровно одну точку пересечения (например, прямая, обозначенная
пунктиром).

Тогда .
Значит, уравнение будет иметь единственный корень при .
.



