Ошибка.
Попробуйте повторить позже
Внутри треугольника взяты точки
так, что
— середина
— середина
— середина
Найдите отношение площадей треугольников
и
Соединим точки и
и
и
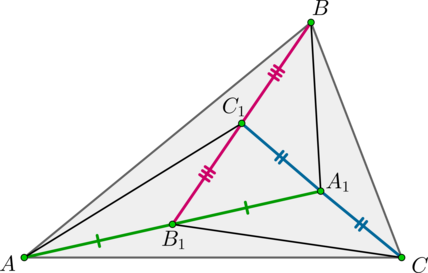
Т.к. медиана делит треугольник на два равновеликих треугольника, то
Аналогично,
Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,
Ошибка.
Попробуйте повторить позже
Точки
лежат на сторонах
соответственно треугольника
причем
Площадь треугольника
равна 15. Найдите площадь треугольника
и
имеют общий угол
, при этом
,
.
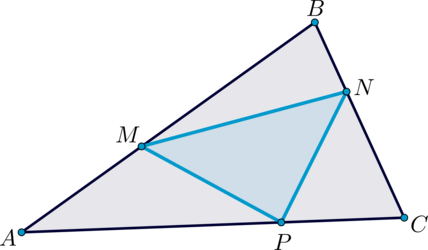
Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то
Аналогично рассуждая, получаем, что
Следовательно,
Ошибка.
Попробуйте повторить позже
Найдите радиусы вписанной и описанной окружностей треугольника со сторонами 13, 14 и 15.
Радиус вписанной окружности вычисляются по формуле
Здесь — площадь треугольника,
— его полупериметр.
Радиус описанной окружности вычисляются по формуле
Здесь ,
и
— длины сторон треугольника,
— его площадь.
![]()
Зная стороны треугольника, найдем его полупериметр:
По формуле Герона вычислим площадь треугольника:
Тогда искомые радиусы равны
Ошибка.
Попробуйте повторить позже
Найдите площадь трапеции с основаниями 11 и 4 и диагоналями 9 и 12.
Сделаем дополнительное постороение. Проведем через прямую, параллельную
,
— точка ее пересечения с
прямой
. Получаем
и
, следовательно,
— параллелограмм. Тогда
,
.
![]()
Рассмотрим теперь треугольник , длины его сторон образует пифагорову тройку
,
следовательно, он прямоугольный с прямым углом
. Пусть
высота из
на
. Тогда можем записать
площадь прямоугольного треугольника
двумя способами
|
SBED = |
Тогда площадь трапеции
|
SABCD = |
54
Ошибка.
Попробуйте повторить позже
Найдите площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные — 17 и 25.
Достроим трапецию до параллелограмма: провередем через прямую, параллельную
,
— точка ее пересечения с
прямой
.
— параллелограмм, следовательно,
,
.
![]()
Найдем косинус угла по теореме косинусов для треугольника
:
Учитывая, что синус угла, меньшего 180, всегда неотрицателен, получаем
Тогда площадь трапеции можно записать следующим образом
450
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
отмечены точки
и
соответственно так, что
Отрезки
и
пересекаются в точке
Найдите площадь треугольника
если площадь
треугольника
равна 63.
Из условия задачи следует, что .
Обозначим Так как
и
имеют одинаковую высоту, опущенную из вершины
то
Аналогично рассуждая, получим
Найдем отношение чтобы определить, какую часть составляет
от
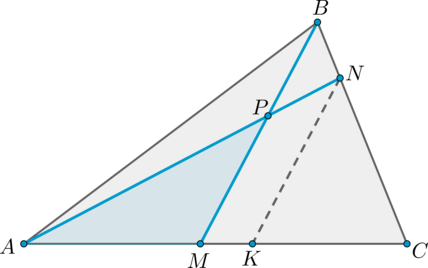
Проведем прямую Тогда по теореме Фалеса
Так как по условию то можно принять
Тогда
По теореме Фалеса имеем:
Так как и
имеют одинаковую высоту, опущенную из вершины
то получаем
Следовательно,
Тогда окончательно имеем:
Ошибка.
Попробуйте повторить позже
Внутри равностороннего треугольника со стороной движется точка. Докажите, что сумма расстояний от этой точки до сторон
треугольника не меняется, и найдите эту сумму.
Рассмотрим равносторонний
– точка внутри треугольника,
— перпендикуляры на стороны
соответственно.
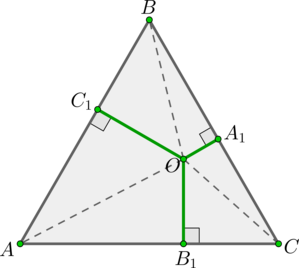
Рассмотрим Их площади равны
соответственно. Тогда сумма их
площадей равна площади всего
следовательно:
Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.
Ошибка.
Попробуйте повторить позже
В треугольнике со сторонами радиус вписанной окружности равен
. Докажите, что
треугольник является прямоугольным.
Как известно, площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. С другой стороны, площадь можно найти по формуле Герона. Следовательно:
Т.к. ,
, то
Таким образом, по обратной теореме Пифагора треугольник будет прямоугольным, причем прямой
угол находится против стороны .
Ошибка.
Попробуйте повторить позже
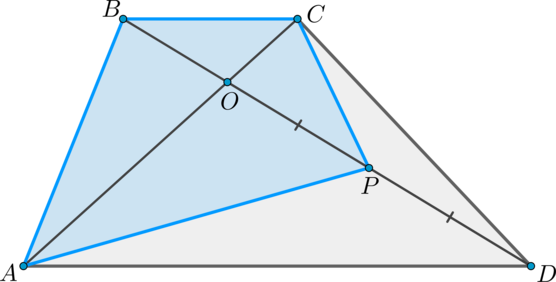
Дана трапеция ее основания
и
равны 2 и 6 соответственно. Диагонали
и
пересекаются в точке
Точка
— середина
Найдите площадь четырехугольника
если
Пусть Заметим, что
по двум углам, так как
как накрест лежащие и
как вертикальные.
Следовательно, запишем отношение подобия:
Тогда для треугольников с общей высотой из вершины имеем:
Аналогично получаем
Для треугольников с общей высотой из вершины имеем:
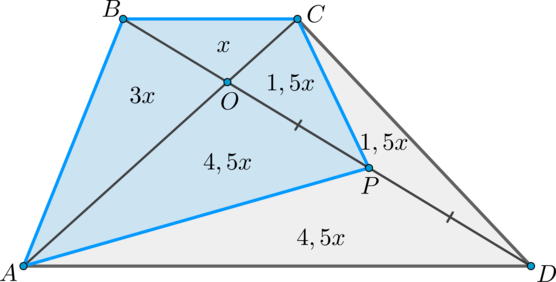
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно,
Так как по условию то окончательно имеем:
Ошибка.
Попробуйте повторить позже
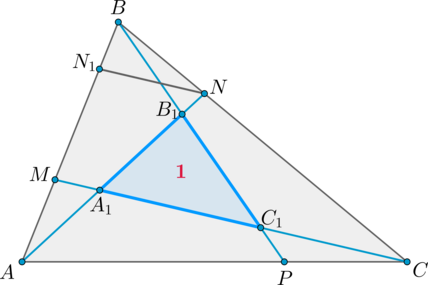
Точки
лежат на сторонах
треугольника
причем
При
пересечении отрезков
образуется треугольник
площадь которого равна 1. Найдите площадь
треугольника
Найдем часть, которую составляет от
Для этого найдем, в каком отношении отрезок
делится отрезком
Проведем
Тогда по обобщенной теореме Фалеса
делит отрезок
в том же отношении, что
делит отрезок
Следовательно, получаем
Также по условию Тогда имеем:
Следовательно, так как треугольники и
имеют общий угол
то их площади относятся как произведения
сторон, образующих этот угол:
Таким образом, Но в свою очередь
и
имеют одинаковую высоту, проведенную из
вершины
Значит, их площади относятся как основания, то есть
Таким образом, получаем
Аналогичным образом получаем, что
Тогда для площади треугольника имеем:
Следовательно,



