Ошибка.
Попробуйте повторить позже
Дан куб . Точка
– середина стороны
, а точка
– середина стороны
. Найдите угол между прямыми
и
. Ответ дайте в градусах.
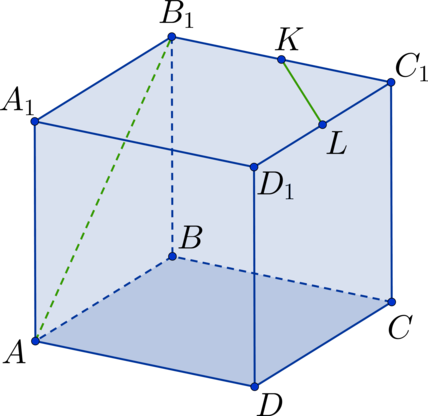
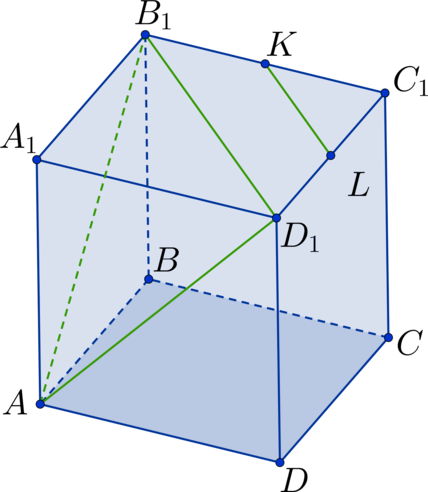
Проведем диагональ в квадрате
. Тогда
– средняя линия в
– искомый угол. Рассмотрим
. Он состоит из диагоналей
соответствующих квадратов
треугольник является равносторонним
.
Ошибка.
Попробуйте повторить позже
Дан куб Найдите угол между прямыми
и
Ответ
дайте в градусах.
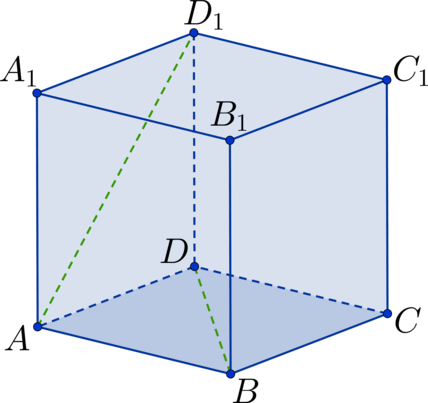
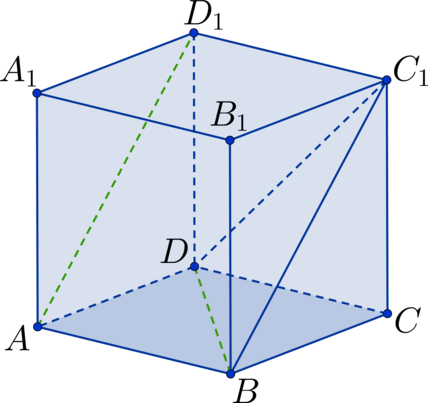
Заметим, что тогда рассмотрим треугольник
в котором
необходимо определить
Он состоит из диагоналей соответствующих
квадратов. Так как квадраты между собой равны, то равны и диагонали,
следовательно,
— равносторонний треугольник. Тогда
Ошибка.
Попробуйте повторить позже
– куб. Найдите угол между прямыми, содержащими отрезки
и
. Ответ
дайте в градусах.
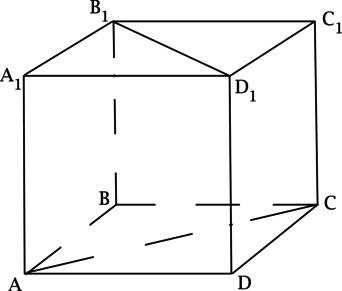
Прямая параллельна прямой
, тогда угол между
и
равен углу между
и
, но
и
– диагонали квадрата, тогда они пересекаются под прямым углом, следовательно
ответ
.
Ошибка.
Попробуйте повторить позже
– куб. На ребрах
и
отмечены точки
и
соответственно таким
образом, что
. Найдите угол между прямыми, содержащими отрезки
и
. Ответ дайте в градусах.
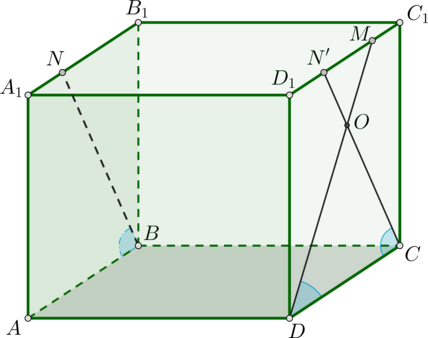
Плоскости и
– параллельны, тогда
параллельна
.
Следовательно, в плоскости
можно провести прямую, параллельную
; пусть
.
Кроме того,
, тогда угол между отрезками
и
равен
и составляет
.
Заметим, что в два угла равны по
, следовательно, и третий
. А по
определению
и есть угол между прямыми
и
.
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с вершиной
. Найдите угол между высотой
пирамиды и ребром
, если высота пирамиды равна
, а сторона основания пирамиды равна
.
Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота
падает в точку пересечения медиан основания.
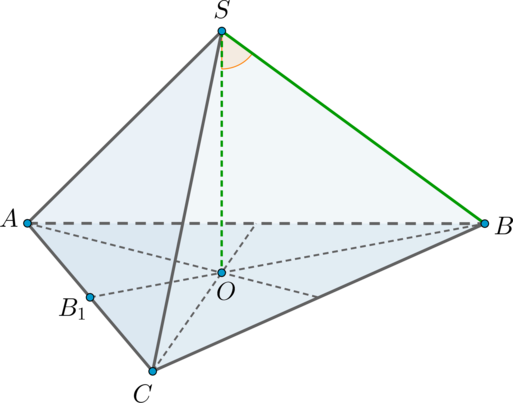
Пусть – медиана, а значит, и высота. По теореме Пифагора
Следовательно, прямоугольный
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с вершиной
. Найдите косинус угла между высотой
основания
и ребром
, если сторона основания равна
, а боковое ребро равно
.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно,
также является и медианой.
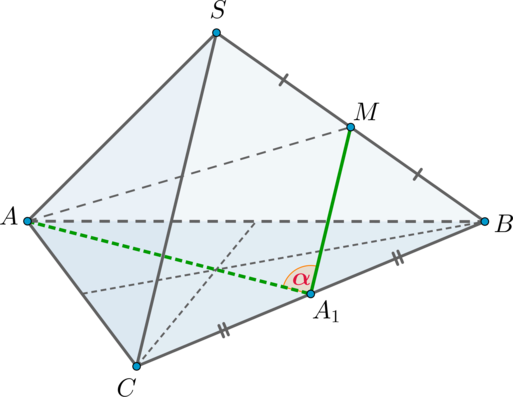
Заметим, что прямые и
скрещиваются. Проведем
, следовательно,
.
Так как и
– середина
, то
– середина
. Следовательно,
– средняя
линия и
Ошибка.
Попробуйте повторить позже
Дан правильный тетраэдр . Найдите квадрат тангенса угла между высотой грани
, опущенной из вершины
, и высотой грани
, опущенной из вершины
.
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные правильные
треугольники, то есть
также является и медианой, значит,
. Также у правильного
тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот)
противоположной грани. Следовательно, если
– высота, то
– точка пересечения медиан
треугольника
, а значит и высот, так как
правильный. Следовательно,
— медиана
и высота.
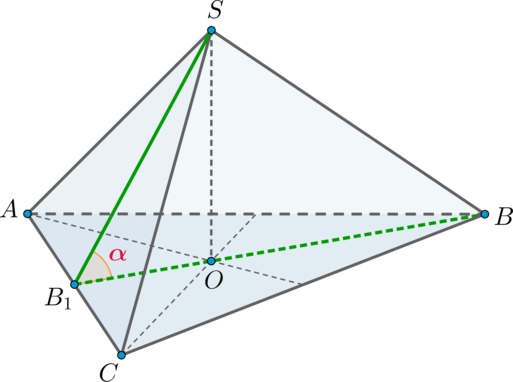
Таким образом, необходимо найти .
Пусть – ребро тетраэдра. Тогда
, следовательно, по теореме Пифагора
Так как
Ошибка.
Попробуйте повторить позже
Точки ,
и
лежат в плоскости
. Прямая
образует с плоскостью
угол в
и проходит
через точку
так, что
. Через
обозначим проекцию
на
. Найдите
, если
. Ответ дайте в градусах.
Докажем, что содержит биссектрису угла
. Выберем на
точку
, а на
точку
так, чтобы
. Построим прямую, проходящую через точку
и точку
– середину
.
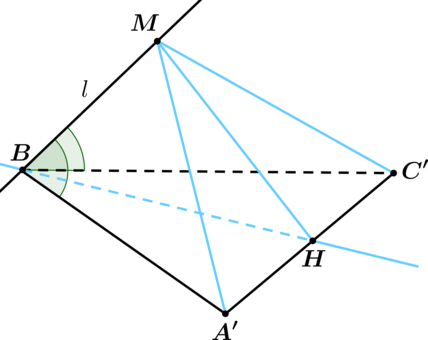
Отметим на точку
. Треугольник
– равнобедренный, тогда
– высота.
Рассмотрим треугольники и
: они равны по двум сторонам и углу между ними, тогда
и треугольник
– равнобедренный, тогда
– его высота.
В итоге и
, следовательно,
. Если предположить, что
–
проекция точки
на
, не попадает на прямую, содержащую
, то получим, что
и
, откуда следует, что
. Но тогда плоскости
и
перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не
может.
Таким образом, лежит на прямой, содержащей
, но тогда
совпадает с прямой,
содержащей
. В итоге,
.
Ошибка.
Попробуйте повторить позже
– куб. Точка
лежит на ребре
. Найдите угол между прямыми, содержащими
отрезки
и
. Ответ дайте в градусах.
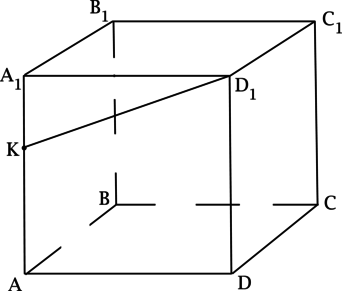
Так как – куб, то
перпендикулярен плоскости
, тогда
перпендикулярен любой прямой, лежащей в плоскости
, следовательно, угол между прямыми,
содержащими отрезки
и
равен
.
Ошибка.
Попробуйте повторить позже
Дан правильный тетраэдр . Найдите
, где
– угол между ребром
и высотой
грани
, опущенной из вершины
.
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные
правильные треугольники, то есть
также является и медианой, значит,
. Также у
правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис,
высот) противоположной грани. Следовательно, если
– высота, то
– точка пересечения медиан
треугольника
, а значит и высот, так как
правильный. Следовательно,
медиана и
высота.
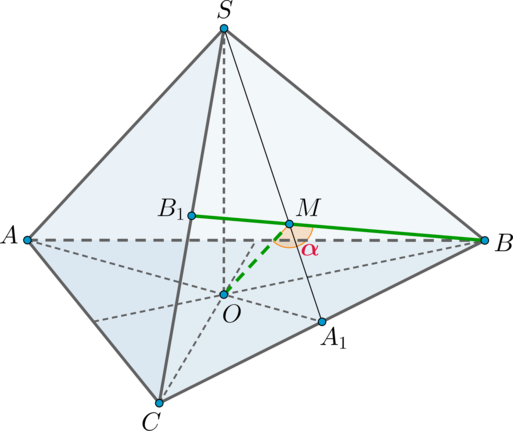
Рассмотрим . Проведем
, следовательно,
.
Заметим также, что будет лежать на
.
Действительно, так как медианы точкой пересечения делятся в отношении , считая от вершины, то
. Следовательно,
(по теореме Фалеса, так как
). Но
и
– медианы в
, следовательно, они пересекаются и точкой пересечения тоже делятся в
отношении
. А так как
делит
в отношении
, считая от вершины
, то
и есть
точка пересечения медиан
и
.
Таким образом, нужно найти .
Пусть – ребро тетраэдра. Тогда



