Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
исходное неравенство равносильно неравенству
Таким образом, исходное неравенство верно на ОДЗ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
исходное неравенство равносильно неравенству
Таким образом,
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
исходное неравенство равносильно неравенству
C учётом ОДЗ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ исходное неравенство равносильно неравенству
Так как на ОДЗ , то исходное неравенство равносильно
неравенству
откуда . Тогда с учётом ОДЗ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки в
строгости неравенства: «» вместо «
» или наоборот. Если в ответ
включено значение переменной, при котором одна из частей неравенства
не имеет смысла, то выставляется оценка «0 баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ определяют три неравенства:
решая которые находим, что
Так как на ОДЗ получаем
Пусть тогда
Найдем нули квадратного трехчлена:
Воспользуемся методом интервалов
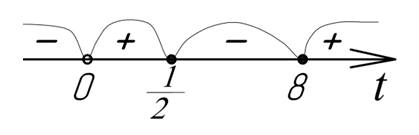
Обратная замена. Обращаем внимание на то, что основание логарифма
поэтому знак неравенства сохраняется:
1 случай.
2 случай.
С учётом ОДЗ
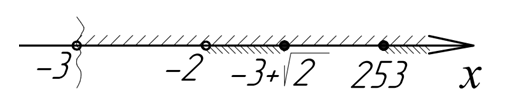
получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
Воспользуемся методом рационализации для логарифмической функции:

С учетом ОДЗ:

| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки в
строгости неравенства: «» вместо «
» или наоборот. Если в ответ
включено значение переменной, при котором одна из частей неравенства
не имеет смысла, то выставляется оценка «0 баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
Найдем ОДЗ для исходного неравенства:
|
|
Первое неравенство является следствием пятого, поэтому его можно опустить. Шестое неравенство входит в третье, поэтому его также можно исключить. Остаётся:
|
|
Первое неравенство верно для любого т.к. квадрат любого числа всегда
неотрицательный, поэтому его можно отбросить. У четвертого неравенства
то есть парабола не имеет пересечений с осью
и всегда
положительна. Поэтому остается только:
|
|
Так как у неравенства дискриминант равен
то решений у неравенства нет.
|
|
|
|
Итоговая ОДЗ:
Мы уже знаем, что квадратный трехчлен не имеет корней, то есть
график параболы всегда находится над осью
и всегда положителен. В
соответствии с этим мы имеем право вынести из основания левого логарифма
степень 2 и при этом не ставить модуль, так как при любом
трехчлен
принимает исключительно положительные значения.
Теперь решим неравенство с помощью метода рационализации:
Отметим нули функции на числовой прямой и применим метод интервалов:
Решением неравенства с учетом ОДЗ будет:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки в
строгости неравенства: «» вместо «
» или наоборот. Если в ответ
включено значение переменной, при котором одна из частей неравенства
не имеет смысла, то выставляется оценка «0 баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
Сделаем замену тогда неравенство примет вид
Найдем ОДЗ. Основание логарифма положительно, поэтому
Кроме того, основание логарифма не равно 1 и знаменатель дроби не равен 0, то есть
Тогда следовательно, неравенство равносильно при этом
условии и на ОДЗ:
Исключая получаем ответ
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
Заметим, что при
, а значит мы можем опустить логарифм с учетом того, что при
выражение не имеет
смысла:
Для начала решим второе неравенство системы:
Обозначим , тогда неравенство примет вид
Решим последнее неравенство методом интервалов:

Получим .
Вернемся к исходным обозначениям:
Тогда система примет вид
Отсюда окончательно получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
Рассмотрим отдельно случаи и
.
1) , тогда
2)
По методу интервалов на :

Таким образом, .
Так как мы рассмотрели все из ОДЗ, то других решений быть не может и окончательный
ответ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Выпишем ОДЗ всех логарифмов:
Решим неравенство на ОДЗ. В числителе оба логарифма распишем по формуле ,
а в знаменателе – по формуле
, а затем по первой формуле:
Ошибка.
Попробуйте повторить позже
Решите неравенство
если ,
и
таковы, что при любом
выполнено
ОДЗ:
Зафиксируем произвольное , тогда
, следовательно,
,
таким образом, при любом
Ошибка.
Попробуйте повторить позже
Решите неравенство
Найдем ОДЗ неравенства:
На ОДЗ исходное неравенство равносильно неравенству
Сделаем замену
По методу интервалов находим Отсюда получаем
Решим неравенство (1) с учетом того, что
Здесь неравенства второй совокупности решаются методом интервалов.
Решим неравенство (2) с учетом того, что
Здесь неравенства второй совокупности решаются методом интервалов.
Объединив решения неравенств (1) и (2), окончательно получим
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
Рассмотрим отдельно случаи ,
и
.
1) , тогда
Таким образом, все идут в ответ.
2) , тогда
Таким образом, среди решений нет.
3) , тогда
Таким образом, все идут в ответ.
Так как мы рассмотрели все из ОДЗ, то других решений быть не может и окончательный
ответ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
исходное неравенство равносильно неравенству
Таким образом, с учётом ОДЗ исходное неравенство верно при
Ошибка.
Попробуйте повторить позже
Решите неравенство
(Задача от подписчиков)
Найдем ОДЗ неравенства:
Решим неравенство на ОДЗ:
Заметим, что так как на ОДЗ , то
, следовательно, основания логарифмов больше
единицы, а значит, оба неравенства системы равносильны
Решая второе неравенство методом интервалов, получим
После пересечения данного множества с и с ОДЗ получим окончательный ответ
Ошибка.
Попробуйте повторить позже
Найдите все такие , которые являются решениями неравенства
при любых
Зафиксируем произвольное .
ОДЗ:
На ОДЗ:
Рассмотрим отдельно случаи и
.
1) , тогда
2)
Так как искомые
Так как , то
, а
, следовательно, последнее неравенство
равносильно неравенству
По методу интервалов на :
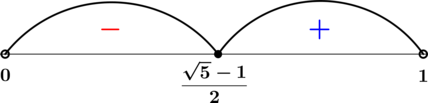
Таким образом, .
Для всякого ,
при
:
Так как мы рассмотрели все из ОДЗ, то других решений быть не может и окончательный
ответ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
если ,
и
таковы, что при любом
выполнено
ОДЗ:
Зафиксируем произвольное , тогда
, следовательно,
,
таким образом, при любом
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ:
На ОДЗ:
исходное неравенство равносильно неравенству
Сделаем замену :
откуда на ОДЗ



