Тригонометрические: на формулы сокращенного умножения —Каталог задач по ЕГЭ - Математика

Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Тригонометрические: на формулы сокращенного умножения

Тема 13. Решение уравнений

13.07 Тригонометрические: на формулы сокращенного умножения

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела решение уравнений

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#16782

Решите уравнение $2 (sinx+ cosx) =2.$

Показать ответ и решение

(sinx+ cosx)2 = 2 2 2 sin x+ 2sinxcosx+ cosx = 2 1 +sin(2x)= 2 sin(2x)= 1 2x= π-+ 2πk, k ∈ℤ 2 x= π-+ πk, k ∈ℤ 4

Ответ:

$π-+ πk, k ∈ℤ 4$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#2058

а) Решите уравнение $sin4x − cos4x= 1. 2$

б) Укажите все его корни, принадлежащие промежутку $( π 11π ) −4-;-4- .$

Показать ответ и решение

а) Применим формулу разности квадратов $a2− b2 = (a − b)(a + b)$ для левой части:

( 2 2 )( 2 2 ) 1 sin x+ cosx sin x− cos x = 2 2 2 1 sin x − cos x= 2 1 − cos2x = 2 1 cos2x= − 2 2π 2x= ± 3-+ 2πk, k ∈ℤ π x =± 3-+ πk, k ∈ ℤ

б) Отберем корни с помощью неравенств.

− π-< π+ πk1 < 11π- ⇒ −-7 < k1 < 29 4 3 4 12 12

Среди целых чисел подходят $k1 = 0, 1, 2,$ при которых получаются корни $π- 4π 7π- x = 3, 3 , 3 .$

− π-< − π-+ πk2 < 11π ⇒ -1 < k2 < 37 4 3 4 12 12

Среди целых чисел подходят $k2 = 1, 2, 3,$ при которых получаются корни $x = 2π, 5π-, 8π . 3 3 3$

Ответ:

а) $± π+ πk, 3$ $k ∈ ℤ$

б) $π-; 2π; 4π; 5π; 7π-; 8π 3 3 3 3 3 3$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Комментарий.

Ответ в задании с развёрнутым ответом – это решение и вывод (называемый ответом).

Ошибка.
Попробуйте повторить позже

Задача 3#414

а) Решите уравнение $cos4 x− sin4x= cosx.$

б) Найдите все его корни, принадлежащие промежутку $[0;2].$

Показать ответ и решение

а) По формуле разности квадратов имеем:

4 4 2 2 2 2 2 2 2 cosx − sin x= (cosx +sin x)(cos x− sin x)= cosx − sin x= 2cos x− 1

Тогда исходное уравнение примет вид

2cos2x− cosx − 1= 0

Сделав замену $t =cosx,$ получим:

2t2− t− 1= 0 ⇒ t1 = 1; t2 = − 1 2

Сделав обратную замену, получим:

⌊ cosx = 1 ⌊x = 2πn, n ∈ℤ ⌈ 1 ⇒ ⌈ 2π cosx = −2 x = ±-3 + 2πm, m ∈ℤ

б) Отберем корни с помощью неравенств.

0 ≤ 2πn≤ 2 ⇒ 0 ≤n ≤ 1- ⇒ n = 0 ⇒ x =0 π

2π 1 1 1 0≤ -3 + 2πm1 ≤ 2 ⇒ − 3 ≤ m1 ≤ π-− 3

Отсюда с учетом $π > 3$ имеем:

1-< 1 ⇒ 1− 1 < 0 ⇒ m ∈∅ π 3 π 3 1

2π 1 1 1 0≤ − 3-+ 2πm2 ≤ 2 ⇒ 3 ≤ m2 ≤ π-+ 3

Отсюда с учетом $π > 3$ имеем:

1+ 1 < 2 ⇒ m ∈ ∅ π 3 3 2

Ответ:

а) $2π ± 3 + 2πm, 2πn, n,m ∈ ℤ$

б) 0

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 4#17306

а) Решите уравнение

( π) ( π) 3 sin x + 6-sin x− 6- + 1= 4

б) Найдите все корни этого уравнения, принадлежащие промежутку $[ π ) − 2;π .$

Показать ответ и решение

а) По формулам синуса суммы и синуса разности имеем:

$pict$

б) Отберем корни с помощью неравенств с учетом $k ∈ℤ.$

π 1 − 2-≤ πk < π ⇔ − 2 ≤k < 1 ⇒ k = 0, x = 0

Ответ:

а) $x = πk, k ∈ℤ$

б) $0$

Ошибка.
Попробуйте повторить позже

Задача 5#16788

а) Решите уравнение $4 4 3 sin x +cos x= 4.$

б) Укажите все его корни, принадлежащие промежутку $(0;π).$

Показать ответ и решение

а)

$4 4 3 4 2 2 4 3 2 2 sin x+ cosx = 4 ⇔ sin x+ 2sin x cos x+ cos x= 4 +2 sin xcos x ⇔ 2 2 2 3 2 2 1 2 2 (sin x+ cos x) = 4 + 2sin x cos x ⇔ 4 = 2sin x cos x ⇔ ⇔ 1= 4sin2 xcos2x ⇔ sin2(2x)= 1 ⇔ sin(2x) =± √1- ⇔ 2 2 |-----2----------| ⇔ 2x= ± π+ πn, n∈ ℤ ⇔ x = ±π-+ πn, n∈ ℤ ⇔ |x= π-+ πn-, n∈ ℤ| 4 8 2 -----8---4-------$

б) Отберем корни с помощью неравенств с учетом $n ∈ ℤ.$

⌊ n= 0, x = π8 || 3π 0 < π+ πn-< π ⇔ − 1 < n< 7 ⇔ − 1< n < 7= 31 ⇔ |||n= 1, x = 8 8 4 8 4 8 2 2 2 |⌈n= 2, x = 58π n= 3, x = 7π 8

Ответ:

а) $π- π- 8 + 4 n, n ∈ℤ$

б) $π-; 3π; 5π; 7π 8 8 8 8$

Ошибка.
Попробуйте повторить позже

Задача 6#16787

а) Решите уравнение $1 sin4x − cos4x = 2$ .

б) Укажите все его корни, принадлежащие промежутку $( π- 11π) − 4; 4$ .

Показать ответ и решение

а)

$4 4 1 2 2 2 2 1 2 2 1 sin x− cos x = 2 ⇔ (sin x− cos x)(sin x+ cos x) = 2 ⇔ cos x − sin x = −|2--⇔-------------| 1 2π- | π- | ⇔ cos(2x) = −2 ⇔ 2x = ± 3 + 2πn, n ∈ ℤ ⇔ x-=-±-3 +-πn,-n-∈-ℤ$

б) Учитываем, что $n ∈ ℤ$ .

⌊ n = 0, x = π3 π- π- 11π-- -7 29 -7 5- || 4π − 4 < 3 +πn < 4 ⇔ −12 < n < 12 ⇔ −12 < n < 212 ⇔ |⌈n = 1, x = 3 n = 2, x = 7π 3

⌊ n = 1, x = 2π π π 11π 1 37 1 1 || 3 −4-< − 3-+ πn < -4-- ⇔ 12 < n < 12 ⇔ 12 < n < 312 ⇔ |⌈n = 2, x = 5π3 n = 3, x = 8π 3

Ответ: $π 2π 4π 5π 7π 8π 3; 3-; 3-; 3-; 3-; -3-$ .

Ответ:

а) $π ± 3-+ πn, n ∈ ℤ$

б) $π- 2π- 4π- 5π- 7π- 8π- 3; 3 ; 3 ; 3 ; 3 ; 3$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#16786

а) Решите уравнение $sin3x − cos3x+ cos2x= 0.$

б) Укажите все его корни, принадлежащие промежутку $[ ] − π;π . 2$

Показать ответ и решение

а)

sin3x− cos3x+ cos2x = 0 2 2 2 2 (sinx− cosx)(sin x + sinxcosx+ cos x)+cos x− sin x = 0 (sinx− cosx)(1+ sin xcosx)+(sin x− cosx)(− cosx− sin x)= 0 (sin x− cosx)(1+ sinx cosx − cosx − sinx)= 0 (sinx − cosx)(1− sinx)(1 − cosx)= 0 ⌊ sinx = cosx |⌈sinx = 1 cosx = 1 ⌊ x= π4 +πk |⌈ x= π2 +2πk , k ∈ ℤ x= 2πk

б) Учитывая, что $k ∈ ℤ,$ сделаем отбор корней:

π π 3 3 π −2-≤ 4-+ πk ≤ π ⇔ − 4 ≤ k ≤ 4 ⇔ k = 0, x= 4-

π π 1 1 1 π −2-≤ 2+2 πk ≤ π ⇔ − 1≤ 2k ≤ 2 ⇔ −2 ≤ k ≤ 4 ⇔ k = 0, x= 2

− π-≤ 2πk ≤ π ⇔ − 1≤ k ≤ 1 ⇔ k =0, x= 0 2 4 2

Ответ:

а) $2πk;$ $π+ πk; 4$ $π+ 2πk, 2$ $k ∈ ℤ$

б) 0; $π 4-;$ $π 2-$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Комментарий.

Ответ в задании с развёрнутым ответом – это решение и вывод (называемый ответом).

Ошибка.
Попробуйте повторить позже

Задача 8#16781

Решите уравнение $1+ sin(2x) =sinx+ cosx.$

Показать ответ и решение

1+ sin(2x)= sinx + cosx 2 2 sin x+ cosx + 2sinx cosx = sinx+ cosx (sinx+ cosx)2 =sinx+ cosx (sin x+ cosx)(sinx +cosx− 1)= 0

$pict$

Ответ:

$− π+ πk; 4$ $2πk;$ $π+ 2πk, 2$ $k ∈ ℤ$

Ошибка.
Попробуйте повторить позже

Задача 9#2442

а) Решите уравнение

sin4 x + cos4x = 3- 4

б) Найдите все его корни, принадлежащие интервалу $(0;π)$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

Добавим и вычтем в левой части уравнения $2sin2x cos2x$ :

4 2 2 4 2 2 3 2 2 2 2 2 3 sin x + 2 sin xcos x + cos x − 2sin x cos x = 4-⇒ (sin x + cos x) − 2sin x cos x = 4-⇒ 3 1 1 − 2sin2x cos2x = --⇒ 4sin2x cos2x = -- 4 2

По формуле двойного угла для синуса $2sinx cosx = sin 2x ⇒ (2sinx cosx)2 = sin22x ⇒ 4 sin2 xcos2 x = sin2 2x$ . Следовательно:

√ -- sin2 2x = 1-⇒ sin 2x = ± --2- 2 2

Отметим точки $√ -- ± --2- 2$ на оси синусов. Получим четыре точки на окружности, в которых находятся все углы, синус которых равен $√ -- --2- − 2$ или $√ -- --2- 2$ .

$PIC$

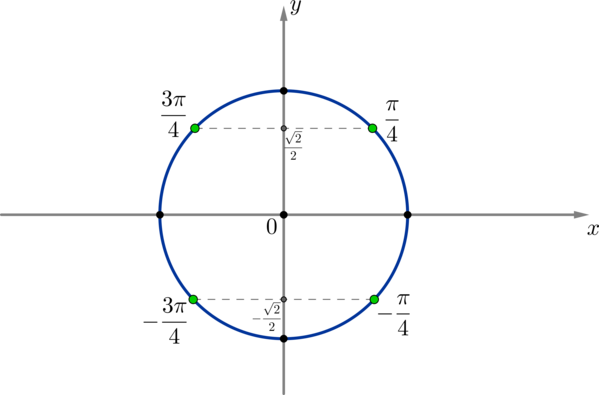
Заметим, что эти четыре точки разбили окружность на четыре равных дуги (длина дуги между любыми двумя соседними точками равна $2π π 4-= 2$ ). Это значит, что все эти точки можно записать в виде одной формулы: $2x = π-+ π-n,∈ ℤ 4 2$ , следовательно:

x = π-+ πn, ∈ ℤ 8 4

б) Отбор корней.

0 < π-+ π-n < π ⇔ − 1-< n < 31- ⇒ n = 0;1;2; 3 ⇒ x = π-; 3π; 5-π; 7π- 8 4 2 2 8 8 8 8

Ответ:

а) $π π --+ -n, ∈ ℤ 8 4$

б) $π- 3π- 5π- 7-π 8; 8 ; 8 ; 8$

Ошибка.
Попробуйте повторить позже

Задача 10#1731

а) Решите уравнение

sin2 x + 4sinx cosx + 4 cos2x = 5

б) Найдите все его корни, принадлежащие отрезку $[ π] 0; -- 2$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

Данное уравнение можно решить, сведя к однородному второй степени. Но мы решим его по-другому. Заметим, что

2 2 2 sin x + 4 sin xcos x + 4cos x = (sin x + 2cos x)

Следовательно, наше уравнение равносильно

√ -- (sin x + 2cos x)2 = 5 ⇒ sinx + 2 cosx = ± 5

Преобразуем левую часть уравнения с помощью формулы вспомогательного угла:

( ) √ -- -1-- -2-- √ -- -1-- sin x + 2cos x = 5 √5--sin x + √5--cosx = 5 sin (x + ϕ), где cos ϕ = √5--

Значит, наше уравнение примет вид:

√-- √ -- 5 sin (x + ϕ) = ± 5 ⇒ sin (x + ϕ) = ±1 ⇒ x + ϕ = π-+ πn, n ∈ ℤ 2

Сделаем постановку $1 ϕ = arccos√--- 5$ и получим окончательный ответ:

π- √1-- x = 2 − arccos 5 + πn, n ∈ ℤ

б) Отберем корни. Т.к. $( ) ( ) √1--> 0 ⇒ arccos √1--∈ 0; π ⇒ π-− arccos√1--∈ 0; π 5 5 2 2 5 2$ .

Следовательно, единственный корень, попадающий в отрезок $[ ] 0; π 2$ — это $x = π-− arccos√1-- 2 5$ при $n = 0$ .

Ответ:

а) $π 1 --− arccos√---+ πn, n ∈ ℤ 2 5$

б) $π 1 --− arccos √--- 2 5$

Ошибка.
Попробуйте повторить позже

Задача 11#1306

а) Решите уравнение

sin6 x + cos6x = 0,25

б) Найдите все его корни, принадлежащие промежутку $(0;1)$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

По формуле сокращенного умножения $a3 + b3 = (a + b)(a2 − ab + b2)$ имеем: $sin6 x + cos6x = (sin2x)3 + (cos2x)3 = (sin2x + cos2x )(sin4x − sin2 xcos2x + cos4 x) =$
$4 2 2 4 = 1 ⋅ (sin x − sin x cos x + cos x )$ .

Добавим и вычтем в скобках $2 sin2 xcos2 x$ и получим:
$sin4 x + 2sin2x cos2x + cos4x − 3sin2x cos2x = (sin2x + cos2 x)2 − 3 sin2 x cos2x =$
$= 1 − 3 sin2 xcos2 x$ .

Таким образом, уравнение преобразуется к виду:

1 − 3sin2x cos2x = 0,25 = ⇒ sin2 xcos2 x = 1- 4

По формуле двойного угла для синуса $1 1 sinα cos α = --sin2α = ⇒ (sin αcos α)2 = --sin22α ⇒ 2 4$ уравнение равносильно:

1 1 π π π --sin2 2x = --= ⇒ sin2 2x = 1 =⇒ sin2x = ±1 =⇒ 2x = --+ πn, n ∈ ℤ = ⇒ x = --+ -n, n ∈ ℤ 4 4 2 4 2

б) Отберем корни:

π- π- 1- -2 1- 0 < 4 + 2n < 1 ⇒ − 2 < n < π − 2

Т.к. $3 < π < 4 ⇒ 1-< 2-< 2- ⇒ 0 < 2-− 1-< 1- 2 π 3 π 2 6$ , следовательно, целые $n$ , удовлетворяющие неравенству, это $n = 0$ . Тогда $π x = -- 4$ .

Ответ:

а) $π π --+ -n, n ∈ ℤ 4 2$

б) $π- 4$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#1191

а) Решите уравнение

sin3x + cos3x = 0

б) Найдите все его корни, принадлежащие промежутку $[ π ] − --;π . 2$

Показать ответ и решение

а) По формуле суммы кубов $a3 + b3 = (a + b)(a2 − ab + b2)$ , а также учитывая, что $sin2x + cos2 x = 1$ , имеем:

[ sin x + cosx = 0 (sin x + cosx )(sin2x − sinx cos x + cos2x) = 0 ⇔ 1 − sin xcos x = 0

Так как $sin x ⋅ cosx = 0,5sin2x$ , то

[ sin x = − cos x | : cos x [tgx = − 1 ⇔ 0, 5sin2x = 1 sin 2x = 2

Второе уравнение не имеет решений, так как $|sin α| ≤ 1$ при любом $α$ . Первое уравнение имеет решения:

π x = − --+ πn,n ∈ ℤ 4

б) Отберем корни:

π- π- 1- 5- π- 3π- − 2 ≤ − 4 + πn ≤ π ⇔ − 5 ≤ n ≤ 4 ⇒ n = 0;1 ⇒ x = − 4; 4

Ответ:

а) $π − --+ πn, n ∈ ℤ 4$

б) $π- 3π- − 4 ; 4$

Ошибка.
Попробуйте повторить позже

Задача 13#987

а) Решите уравнение $cosx− sinx + 1+ 2sinxcosx =0.$

б) Укажите все его корни, принадлежащие промежутку $(−7π;−3π).$

Показать ответ и решение

а) Преобразуем уравнение к виду

cosx − sinx− (1− 2sinx cosx)+ 2= 0

Тогда по формуле сокращенного умножения $(sinx− cosx)2 = 1− 2sinx cosx$ можно записать:

−(sinx − cosx)− (sinx − cosx)2+ 2= 0

Сделаем замену переменной $t= sinx− cosx.$ Тогда уравнение примет вид

− t− t2+ 2 =0 ⇒ t2+ t− 2= 0 ⇒ t1 = −2, t2 =1

Сделаем обратную замену переменной.

√- √- sinx− cosx= − 2 |:√2 ⇒ -2-sinx − -2cosx =− √2 ⇒ 2 2

( ) ⇒ sin xcos π− cosxsin π-=− √2 ⇒ sin x− π- = −√2 4 4 4

Так как область значений синуса — это отрезок $[−1;1],$ то данное уравнение не имеет решений, так как $- − √ 2< −1.$

√ - √2- √2 √2 ( π) √2 sinx− cosx= 1 |: 2 ⇒ -2-sin x− -2-cosx= -2- ⇒ sin x − 4- = 2-- ⇒

⌊x− π-= π-+2πn, n∈ ℤ ⌊ π- ⇒ |⌈ 4 4 ⇒ ⌈x= 2 + 2πn, n ∈ℤ x− π-= 3π +2πm, m ∈ ℤ x= π +2πm, m ∈ ℤ 4 4

б) Отберем корни с помощью неравенств.

π 15 7 −7π < 2 + 2πn <− 3π ⇒ − 4-< n< − 4

Таким образом, среди целых чисел подходят только $n = −3;−2,$ при которых получаются корни $11π 7π x= −-2- ;− 2-.$

− 7π < π+ 2πm < −3π ⇒ −4< m < − 2

Таким образом, среди целых чисел подходит только $m = −3,$ при котором получается корень $x =− 5π.$

Ответ:

а) $π+ 2πn;π+ 2πm;n,m ∈ ℤ 2$

б) $− 11π ; −5π; − 7π 2 2$

Ошибка.
Попробуйте повторить позже

Задача 14#774

а) Решите уравнение

tg2x − 2 sin x + cos2x = 0

б) Укажите все его корни, принадлежащие промежутку $[2π;3π ]$ .

Показать ответ и решение

а) Т.к. $sinx tgx = ----- cos x$ , то уравнение можно переписать в виде:

$( sin x)2 sin2x − 2sinx cos2x + cos4x ----- − 2sinx + cos2 x = 0 ⇒ ---------------2------------- = 0 ⇒ cosx cos x$

$( 2 )2 2 ⇒ sinx-−--cos-x = 0 ⇒ sinx-−-cos--x = 0 ⇒ cos x cos x$

${ 2 { 2 sinx − cos x = 0 sin x − 1 + sin x = 0 ⇒ cos x ⁄= 0 ⇒ cos x ⁄= 0$

Первое уравнение с помощью замены $sin x = t$ сводится к квадратному, корнями которого являются

√ -- √ -- t = −-1 −---5 и t = −-1 +---5 1 2 2 2

Корень $t1$ не подходит, т.к. область значений синуса от $− 1$ до $1$ , а $√ - −1−2--5< − 1$ . Делаем обратную замену:

⌊ √5--− 1 √5--− 1 | x = arcsin------- + 2 πn,n ∈ ℤ sin x = ------- ⇒ | 2 √ -- 2 ⌈ --5 −-1 x = π − arcsin 2 + 2πm, m ∈ ℤ

Заметим, что для этих корней выполнено $cosx ⁄= 0$ (т.к. если $cosx = 0$ , то $sin x$ равен $± 1$ ).

б) Отберем корни.

Обозначим $√ -- --5-−-1 arcsin 2 = α$ . Тогда

α 3 α 2π ≤ α + 2 πn ≤ 3π ⇒ 1 − ---≤ n ≤ --− --- 2π 2 2π

Заметим, что т.к. $π- π- 6 < α < 2$ (т.к. $1 √5−1- 2 < 2 < 1$ ), то

$1--< α--< 1- 12 2π 4$ . Следовательно, $1 − -α- = 0,... 2 π$ , $3− α--= 1,... 2 2π$

Следовательно, среди целых чисел нам подходит только $n = 1$ , при котором получаем корень $√- x = α + 2π = arcsin -52−1-+ 2π$ .

1 α α 2π ≤ π − α + 2πm ≤ 3π ⇒ 2-+ 2-π ≤ m ≤ 1 + 2π-

Аналогично получаем, что $1- -α- 2 + 2 π = 0,...$ , $-α- 1 + 2π = 1,...$

Таким образом, среди целых подходит только $m = 1$ , откуда получаем корень $√- x = π − α + 2π = 3π − arcsin -5−21-$ .

Ответ:

а) $√- √- arcsin -52−1-+ 2πn; π − arcsin -5−21-+ 2πm; n, m ∈ ℤ$

б) $√- √- arcsin -5−1-+ 2π; 3 π − arcsin -5−-1 2 2$

Ошибка.
Попробуйте повторить позже

Задача 15#773

а) Решите уравнение

( ) √- √--1--- (sin x + cosx) (1 + sin 2x) = log 2+1 2 − 1

б) Укажите все его корни, принадлежащие промежутку $(12;14 )$ .

Показать ответ и решение

а) Сделаем преобразования с правой частью:

( -- ) ( -- ) ( 1 ) √ 2 + 1 √2 + 1 √-- log√2+1 √------ = log√2+1 √--------√-------- = log√2+1 ------- = log√2+1 ( 2 + 1) = 1 2 − 1 ( 2 − 1)( 2 + 1) 2 − 1

Значит, уравнение перепишется в виде:

$(sin x + cosx)(1 + sin 2x) = 1 ⇒ (sinx + cos x)(1 + 2sinx cosx ) = 1 ⇒$

$⇒ (sinx + cos x)(sin2 x + 2sin xcos x + cos2x) = 1 ⇒ (sinx + cos x)3 = 1 ⇒$

(последнее преобразование сделано по формуле сокращенного умножения)

$√ -- √ -- √ -- √ -- √ -- --2- --2- --2- ( π-) --2- ⇒ sin x + cosx = 1 | : 2 ⇒ 2 sin x + 2 cosx = 2 ⇒ sin x x + 4 = 2$

$⌊ π π ⌊ x + --= --+ 2πn, n ∈ ℤ x = 2πn, n ∈ ℤ | 4 4 ⌈ ⌈ π 3π ⇒ x = π-+ 2 πm, m ∈ ℤ x + --= ---+ 2πm, m ∈ ℤ 2 4 4$

б) Отберем корни.

6 7 12 < 2πn < 14 ⇒ --< n < -- π π

Т.к. $3 < π < 3,5$ , то $12 < 6 < 2 7 π$ и $2 < 7 < 7 π 3$ , то есть, условно говоря,

$6 π = 1,...$

$7 = 2,... π$

Таким образом, среди целых чисел подходит только $n = 2$ , который дает корень $x = 4π$ .

π 6 1 7 1 12 < 2-+ 2πm < 14 ⇒ π-− 4-< m < π-− 4-

Из выведенных данных предыдущего пункта можно также условно сказать, что

$6 1 --− --= 1,... π 4$

По поводу $7 − 1 π 4$ точного значения не получается (с той оценкой, которую мы сделали, получается, что это число из промежутка $(1,...;2,...)$ ), поэтому необходимо точнее оценить $π$ :

$314-< π < 315- ⇒ 700-< 7-< 700- ⇒ 100 100 315 π 314$

$71 7 1 1243 7 1 ⇒ ---< --− --< ----- ⇒ 1 3536-< --− --< 1661258 36 π 4 628 π 4$

Таким образом, условно можно сказать, что $7- 1- π − 4 = 1, ...$

Значит, можно сказать, что $1,... < m < 1,...$ , то есть это неравенство не имеет решений в целых числах.

Ответ:

а) $π 2πn; --+ 2πm; n,m ∈ ℤ 2$

б) $4π$

Ошибка.
Попробуйте повторить позже

Задача 16#772

а) Решите уравнение

sin3 x − cos3x + cos 2x = 0

б) Укажите все его корни, принадлежащие промежутку $[ π ] − -;π 2$ .

Показать ответ и решение

а) По формулам сокращенного умножения:

$sin3 x − cos3x = (sin x − cosx)(sin2x + sinx cosx + cos2 x) = (sin x − cosx )(1 + sinx cosx )$ ;

$2 2 cos2x = cos x − sin x = (cos x − sin x)(cosx + sinx )$ .

Значит, уравнение можно переписать в виде:

(sinx − cos x)(1 + sin xcos x) + (cosx − sinx)(cos x + sin x) = 0 ⇒ ⇒ (cos x − sin x)(− 1 − sin xcos x + cosx + sinx ) = 0 ⇒ [ ⇒ cosx − sin x = 0 − 1 − sin x cosx + cosx + sinx = 0

Решим каждое уравнение по отдельности.
1) Первое уравнение является однородным и решается делением обеих частей уравнения, например, на $cosx$ :

cos-x − sinx- = 0 ⇒ 1 − tgx = 0 ⇒ tgx = 1 ⇒ x = π-+ πn,n ∈ ℤ cos x cosx 4

2) Второе уравнение решается разложением на множители:

$− 1 − sinx cosx + cos x + sin x = 0 ⇒ sin x − 1 − (sin xcos x − cosx) = 0 ⇒$

$⇒ (sinx − 1 ) − cos x(sin x − 1) = 0 ⇒ (sin x − 1)(1 − cosx ) = 0 ⇒$

$[ ⌊ π- sin x = 1 ⌈x = 2 + 2πm, m ∈ ℤ cosx = 1 ⇒ x = 2πk,k ∈ ℤ$

б) Отберем корни по окружности:

$PIC$

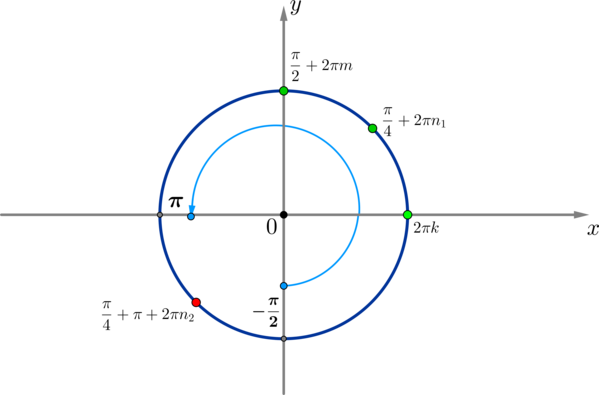
Заметим, что одна точка, задающая серию корней $π 4 + π + 2πn2$ из решения первого уравнения, не входит в отрезок $[ ] − π2;π$ .

Нетрудно увидеть, что из остальных точек в этот отрезок попадает по одному углу: $0$ (при $k = 0$ ), $π 4$ (при $n1 = 0$ ) и $π 2$ (при $m = 0$ ).

Ответ:

а) $π π 2πk; --+ πn; --+ 2πm; n,m, k ∈ ℤ 4 2$

б) $0; π; π- 4 2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#413

а) Решите уравнение

3 3 sin 2x− cos 2x = sin2x − cos2x

б) Найдите сумму его корней, принадлежащих промежутку $[− π;π) 4$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

По формуле сокращенного умножения $a3− b3 =(a− b)(a2+ ab+ b2)$ имеем: $sin32x − cos32x= (sin2x − cos2x)(sin22x + sin2xcos2x+ cos22x)=$
$= (sin 2x− cos2x)(1+ sin2xcos2x)$ .

Таким образом, уравнение примет вид:

(sin2x − cos2x)(1+ sin 2xcos2x)− (sin2x − cos2x)= 0⇒ (sin 2x− cos2x)sin 2xcos2x = 0

По формуле двойного угла для синуса $sin αcosα= 1 sin2α 2$ уравнение преобразуется к виду:

1 (sin2x − cos2x)⋅2 sin4x= 0 ⇒

[ sin2x− cos2x= 0 [tg2x= 1 ⌊x = π-+ πm,m ∈ ℤ ⇒ ⇒ ⌈ 8π 2 sin4x= 0 4x= πn,n ∈ℤ x = 4n,n ∈ℤ

б) Отберем корни:

− π-≤ π-+ πm < π ⇒ − 3 ≤ m < 7 4 8 2 4 4

Целые $m$ , удовлетворяющие данному неравенству, это $m = 0;1$ . Им соответствуют углы $π; 5π 8 8$ .

π- π- − 4 ≤ 4n < π ⇒ − 1≤ n <4

Целые $n$ , удовлетворяющие данному неравенству, это $n = −1;0;1;2;3$ . Им соответствуют углы $π- π-π- 3π − 4;0;4; 2;4$ .

Таким образом, сумма всех корней, принадлежащих промежутку:

π+ 5π − π-+0 + π+ π-+ 3π =2π 8 8 4 4 2 4

Ответ:

а) $π+ π-m, πn, n,m ∈ℤ 8 2 4$

б) $2π$

Ошибка.
Попробуйте повторить позже

Задача 18#412

а) Решите уравнение

sin4 x − cos4x + cos2x = sin x + cosx

б) Найдите все его корни, принадлежащие промежутку $( ) − 5π;0 2$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

Т.к. по формуле сокращенного умножения $a2 − b2 = (a − b)(a + b)$ выражение $sin4 x − cos4x = (sin2x − cos2 x)(sin2 x + cos2x) = (sin2 x − cos2x ) ⋅ 1$ , а по формуле косинуса двойного угла $2 2 cos2x = cos x − sin x$ , то уравнение примет вид:

sin2 x − cos2x + cos2 x − sin2 x = sin x + cosx ⇒ 0 = sin x + cosx

Полученное уравнение является однородным первой степени и решается делением обеих частей равенства на $cosx$ :

π- tgx = − 1 ⇒ x = − 4 + πn, n ∈ ℤ

б) Отберем корни:

5π- π- 9- 1- − 2 < − 4 + πn < 0 ⇒ − 4 < n < 4 ⇒ n = − 2;− 1;0

Значит, корни, принадлежащие данному промежутку — это $− 9π-;− 5π-;− π- 4 4 4$ .

Ответ:

а) $π − --+ πn, n ∈ ℤ 4$

б) $9π- 5π- π- − 4 ;− 4 ;− 4$

Ошибка.
Попробуйте повторить позже

Задача 19#411

а) Решите уравнение

cos2x + cos x + sin x = 0

б) Найдите все его корни, принадлежащие интервалу $(0; π)$ .

Показать ответ и решение

а) ОДЗ: $x$ – произвольное. Решим на ОДЗ.

Применим формулу косинуса двойного угла: $cos2x = cos2x − sin2x = (cos x − sin x)(cosx + sinx )$ :

(cos x − sin x)(cosx + sinx ) + (cos x + sin x) = 0 ⇒ (cos x + sin x)(cosx − sin x + 1) = 0 ⇒

[ cosx + sinx = 0 cosx − sinx = − 1

Первое уравнение является однородным первом степени, поэтому путем деления правой и левой частей равенства на $cosx$ сводится к $π tgx = − 1 ⇒ x0 = − --+ πn, n ∈ ℤ 4$