Тригонометрические/показательные/логарифмические: смешанного типа —Каталог задач по ЕГЭ - Математика

Главная
Каталог задач
Каталог заданий по ЕГЭ - Математика
Тригонометрические/показательные/логарифмические: смешанного типа

Тема 13. Решение уравнений

13.12 Тригонометрические/показательные/логарифмические: смешанного типа

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела решение уравнений

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#20788

а) Решите уравнение $( ) log 1 2sin2x− 3cos2x+ 6 = − 2. 3$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ 7π ] −-2 ;−2π .$

Показать ответ и решение

а)

$pict$

б) Проведём отбор с помощью двойного неравенства в каждой серии по отдельности.

$pict$

Получим корни: при $k = −3$ имеем $x = −31π, 3$ при $k = − 2$ имеем $x = −21π. 3$

$pict$

Получим корни: при $k = −3$ имеем $2 x= − 23π.$

Ответ:

а) $± π+ πk, k ∈ ℤ 3$

б) $10π 8π 7π − 3 ;− 3 ;− 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#85241

а) Решите уравнение

( √-) ( √-) log1 sinx + -5- + log1 sinx − -5- = 2 3 6 3 6

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ π] −π;2- .$

Показать ответ и решение

а) Уравнение равносильно системе

( ( ) ||{ log sin2x − 5- = 2 13 √- 36 ||( sinx − -5-> 0 6 ( 5 1 |{ sin2x − 36 = 9 | √5 ( sinx − -6-> 0 ( |{ sin2x = 1 √4 |( sinx − -5-> 0 6 ( 1 |{ sinx = ±2 |( √5- sinx − 6 > 0 sinx= 1 2 ⌊ π- |⌈x = 6 + 2πn,n ∈ ℤ x= 5π + 2πn,n ∈ ℤ 6

б) Отберем корни с помощью тригонометрической окружности. Для этого отметим на ней дугу, соответствующую отрезку $[ π ] −π;2- ,$ концы этой дуги и решения, которые лежат на ней.

$ππ- 2−6 π$

Следовательно, на отрезке $[ ] − π; π 2$ лежит число $π. 6$

Ответ:

а) $π+ 2πn, 5π+ 2πn, n ∈ ℤ 6 6$

б) $π 6-$

Ошибка.
Попробуйте повторить позже

Задача 3#85237

а) Решите уравнение $log (3sin4x + cos4x +2)= 4 +log 3. cosx cosx$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[− 3π;2π].$

Показать ответ и решение

а) Уравнение равносильно

log (3sin4x + cos4x+ 2)= log (3cos4x) cosx cosx

Выпишем ограничения на основания логарифмов:

( { cosx > 0 ( cosx ⁄= 1

При этих ограничениях уравнение равносильно

3sin4x+ cos4x+ 2= 3cos4x 2 2 2 2 2 3(sin x − cos x)(sin x+ cos x)+ 2cos 2x− 1+ 2= 0 2cos22x− 3cos2x+ 1= 0 ⌊ ⌈cos2x= 1 cos2x= 1 ⌊ 2 |x= πm, m ∈ℤ |⌈ π x= ± 6-+πn,n ∈ ℤ

Учитывая ограничения, изобразим полученные серии на окружности:

$−−π2π5πππ+5+mπ++22π2π+2mπn2πnπnn 6666$

Таким образом, $π x = ±6-+ 2πn,n∈ ℤ.$

б) Отберем корни с помощью неравенств.

Для первой серии имеем:

−3π ≤ π+ 2πn ≤2π ⇒ n= −1;0 ⇒ x = − 11π; π 6 6 6

Для второй серии имеем:

π 13π π 11π −3π ≤ − 6 + 2πn ≤ 2π ⇒ n= − 1;0;1 ⇒ x =− -6-;−-6;-6-

Ответ:

а) $± π+ 2πn,n ∈ℤ 6$

б) $13π 11π π π 11π − -6- ;− -6-;−6-;6;-6-$

Ошибка.
Попробуйте повторить позже

Задача 4#83756

а) Решите уравнение

log cos2x =log (cos2x − cosx+ sin xcosx) cosx cosx−0,5

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ ] − 3π; 5π . 2 2$

Показать ответ и решение

а) Уравнение равносильно

( ||||cosx> 0 ||||cosx⁄= 1 ( ||||| |||| cosx > 0,5 {cos2x> 0 ⇔ { cosx ⁄= 1 |||cosx− 0,5> 0 ||| ( 1)2 |||| |( cosx− 2 = cos2x− cosx+ sinx cosx |||||cosx− 0,5⁄= 1 |(2 = logcosx−0,5(cos2x− cosx+ sinx cosx)

Рассмотрим второе уравнение:

2 1 2 cos x− cosx+ 4 =cos x− cosx+ sinx cosx sinxcosx= 1 4 sin2x= 1 ⌊ π2 | x= 12 + πn,n ∈ ℤ |⌈ x= 5π + πm,m ∈ ℤ 12

Пересечем полученный ответ с условиями $cosx> 0,5$ и $cosx⁄= 1 :$

$π- 12 + 2πn$

Следовательно, $x = π-+ 2πn,n∈ ℤ. 12$

б) Отберем корни на отрезке $[ 3π 5π] − 2-;-2$ с помощью неравенства:

3π π 5π 19 29 − 2-≤ 12-+ 2πn≤ -2 ⇔ −24 ≤ n≤ 24

Так как $n ∈ℤ,$ то $n =0;1.$ Следовательно, $x = π-; 25π. 12 12$

Ответ:

а) $π-+ 2πn,n∈ ℤ 12$

б) $π 25π 12;-12$

Ошибка.
Попробуйте повторить позже

Задача 5#82246

а) Решите уравнение

( ) log22-12 sin-x+-cosx 3 log2cosx + log2cos x+ 4= 4log2(sinx +2 cosx)

б) Найдите все корни этого уравнения, принадлежащие отрезку $[0;2π].$

Показать ответ и решение

а) Преобразуем уравнение:

( ) log22-12 sinx+-cosx log2cosx + 3log2cosx= 4 (log2(sinx + 2cosx)− 1) ( ) ( ) log22-12 sinx+-cosx-+ 3log cosx= 4 log 1 sinx +cosx log2cosx 2 2 2

Сделаем замену $( ) a = log2 12 sinx+ cosx ,$ $b= log2cosx.$ Тогда $b⁄= 0$ и уравнение примет вид

2 a-+ 3b= 4a |:b⁄= 0 b (a )2 a b − 4⋅b +3 =0 ⌊ | a= 3 |⌈ b a= 1 b

Заметим, что

a log2(1sin x+ cosx) ( 1 ) b =-----2log-cosx---- = logcosx 2 sin x+ cosx 2

Сделаем обратную замену:

(⌊ 1 ||||| 2 sin x+ cosx = cos3x ⌊ (1 ) |||||⌈ 1 |logcosx 2 sinx+ cosx =3 |||{ 2 sin x+ cosx = cosx |⌈ ( ) ⇔ 1sinx + cosx > 0 logcosx 1 sinx+ cosx =1 ||||| 2 2 ||||cosx >0 ||(cosx ⁄=1

Получаем

(|⌊ sinx = 2cosx(cos2 x− 1) (|⌊ (2 sinxcosx+ 1)sin x= 0 (| ⌊sin x= 0 |||||⌈ |||||⌈ ||||| ⌈ { sinx = 0 { sinx = 0 { sin 2x= −1 |||cosx> 0 ⇔ |||cosx> 0 ⇔ ||| cosx > 0 |||( |||( |||( cosx⁄= 1 cosx⁄= 1 cosx ⁄= 1

Тогда

(||⌊ |||||| x= πn,n ∈ℤ ||{⌈ π- π | x= − 4 + πn,n ∈ℤ ⇔ x= − 4-+2πm, m ∈ℤ ||||cosx >0 |||( cosx ⁄=1

б) Отберем корни с помощью неравенства:

π 7π 0≤ −-4 + 2πm ≤ 2π ⇒ m = 1 ⇒ x= 4-

Ответ:

а) $− π+ 2πm, m ∈ℤ 4$

б) $7π -4$

Ошибка.
Попробуйте повторить позже

Задача 6#82105

а) Решите уравнение

√---------- ∘----------- 5c2o2sx−2tg2x−12−3 c1o1sx−3−tg2x − --2-4-11----=51+3 c1os1x− co1s2x−2 5tg x−cosx+6

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ 5π] π;2- .$

Показать ответ и решение

а) Заметим, что $1+ tg2x = --12-, cos x$ откуда $tg2x = -12-− 1. cos x$ Следовательно, уравнение примет вид

∘----------- ∘----------- 5c2o2sx− co2s2x− 10−3 c1o1sx− co1s2x−2 − 4 ⋅5 1co1sx−co1s2x−5 = 5⋅53 c11osx−co1s2x−2

Заметим, что можно сделать замену

∘--------------- (|| -11-- --1-- ||||y = cosx − cos2x − 2 { y2−3 |||a = 5 |||( 3y b =5

Учтем, что $y ≥ 0,$ $a> 0,$ $b> 0.$

Тогда уравнение примет вид

a2 − 4a − 5b= 0 |:b b ( a)2 a ( a ) b − 4⋅b − 5 = 0 t= b >0 t2− 4t − 5 =0 ⌊ ⌈ t= −1 t= 5 a b = 5 5y2− 3y−3 = 5 y2− 3y− 4= 0 ⌊ ⌈ y = −1 y = 4 y = 4

Сделаем обратную замену, положив $z = c1osx :$

∘ ---------- 11z − z2 − 2 = 4 z2− 11z+ 18 = 0 ⌊ ⌈ z = 2 z = 9

Следовательно, получаем

⌊ 1 ⌊ π- || cosx = 2 ||x =± 3 + 2πn,n ∈ ℤ ⌈ 1 ⇔ ⌈ 1 cosx = 9 x =± arccos9 + 2πm,m ∈ ℤ

б) Отберем корни с помощью тригонометрической окружности. Для этого отметим на ней дугу, соответствующую отрезку $[ ] π; 5π , 2$ концы этой дуги и решения, которые лежат на ней.

$557πππ 1 1 π−a2 arc33rccocso9s9+ +2π2π$

Следовательно, на отрезке $[ ] π; 5π 2$ лежат числа

− arccos 1 + 2π; 5π; 7π; arccos 1+ 2π 9 3 3 9

Ответ:

а) $± π+ 2πn,n ∈ℤ; ±arccos 1+ 2πm,m ∈ ℤ 3 9$

б) $1 5π 7π 1 − arccos9 + 2π;-3 ;-3 ; arccos9 + 2π$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#81535

а) Решите уравнение $( 2 )6sin2x+11cosx+1 1 − 5 cosx = 1.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ ] π;2π . 2$

Показать ответ и решение

а) Сделаем замену $cosx= y,$ тогда уравнение примет вид

( 2 )7+11y−6y2 1− 5 y =1 ⌊(| 2 |{ 1− 5y > 0 |||( 2 |⌈ 7+211y− 6y = 0 1 − 5y = 1 ⌊(| 5 |{ y < 2 |||( 2 |⌈ 6y − 11y − 7 = 0 y = 0 ⌊( 5 |||||| y < 2 |||{ ⌊ 1 ||||| |y = −2 |||||| |⌈ 7 |⌈( y = 3 y = 0 ⌊ y = 0 || |||y = − 1 |⌈ 2 y = 7 3

Так как $y = cosx∈ [−1;1],$ то получаем

⌊ ⌊ π- | y = 0 || x= 2 + πn,n ∈ ℤ ⌈ 1 ⇒ ⌈ 2π- y = −2 x= ± 3 + 2πm,m ∈ ℤ

б) Отберем корни с помощью тригонометрической окружности. Для этого отметим на ней дугу, соответствующую отрезку $[ ] π;2π , 2$ концы этой дуги и решения, которые лежат на ней.

$π2324ππππ 2233$

Следовательно, на отрезке $[π-;2π ] 2$ лежат числа $π; 2π ; 4π-; 3π. 2 3 3 2$

Ответ:

а) $π+ πn,n ∈ℤ;± 2π+ 2πm,m ∈ ℤ 2 3$

б) $π 2π 4π 3π 2-;3-;3-;-2$

Ошибка.
Попробуйте повторить позже

Задача 8#81523

а) Решите уравнение $log sinx+ log sinx= log sin2x⋅log √sinx. 2 3 2 3$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ 5π] −1;-2 .$

Показать ответ и решение

а) ОДЗ уравнения: $sinx> 0.$ Сделаем замену $sin x= y,$ тогда уравнение примет вид

1 log2y + log3y = 2log2y⋅2 log3y log2y + log32⋅log2y = log2y⋅log3y l⌊og2y(1+ log32 − log3y)= 0 log y = 0 ⌈ 2 log3y = 1+ log32= log36 ⌊ y = 1 ⌈ y = 6

Так как $y ∈ (0;1],$ то

y = 1 ⇒ sinx= 1 ⇔ x = π-+2πn,n∈ ℤ 2

б) Отберем корни с помощью тригонометрической окружности. Для этого отметим на ней дугу, соответствующую отрезку $[ 5π] −1;-2 ,$ концы этой дуги и решения, которые лежат на ней.

Заметим, что $π ∈(3,1;3,2),$ следовательно, $( ) 1∈ 0; π . 2$

$π−1;−1+ 2π 2$ $−5π1+ 2π 2$

Следовательно, на отрезке $[ ] − 1; 5π 2$ лежат числа $π-; 5π. 2 2$

Ответ:

а) $π+ 2πn, 2$ $n ∈ ℤ$

б) $π 2-;$ $5π -2$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 9#78010

а) Решите уравнение $√- (cos2x− 13 2 sinx+ 13)⋅log13(sin22x)= 0.$

б) Найдите все его корни, принадлежащие отрезку $[ ] 3π; 9π . 2$

Показать ответ и решение

Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а другие при этом не теряют смысла. Уравнение определено, если $sin22x> 0.$ Рассмотрим два случая:
1)

cos2x− 13√2sin x+ 13= 0,

1− 2sin2 x− 13√2-sin x+ 13= 0,

−2sin2x− 13√2sin x+ 14= 0.

Сделаем замену $t =sinx:$

√- −2t2− 13 2t+ 14= 0,

√- 2t2+ 13 2t− 14= 0,

√ - D = (13 2)2 − 4 ⋅2 ⋅(− 14) =338+ 112= 450,

√ - √--- √- √- √ - t1 = −13-2−--450 = −13-2−-15-2-= −-28--2= − 7√2, 2 ⋅2 4 4

√ - √--- √- √- √ - √ - t1 = −13-2+--450 = −13-2+-15-2-= 2--2= --2. 2 ⋅2 4 4 2

Сделаем обратную замену:
1а)

√- sinx = −7 2.

Это уравнение не имеет решений, так как $√- − 7 2< − 1.$
1б)

√2 sinx = 2-,

x= π-+ 2πn, n ∈ℤ 4

x= 3π-+ 2πn, n ∈ ℤ. 4

2 log13(sin 2x)= 0,

2 0 sin 2x =13 ,

sin22x= 1,

sin2x= ±1,

2x = π-+πn, n ∈ℤ, 2

π- πn- x = 4 + 2 .

Все найденные решения удовлетворяют ограничению $2 sin 2x > 0.$

б) Отберём корни, принадлежащие отрезку $[ 9π] 3π;-2 .$ Для отбора корней воспользуемся тригонометрической окружностью:

$PIC$

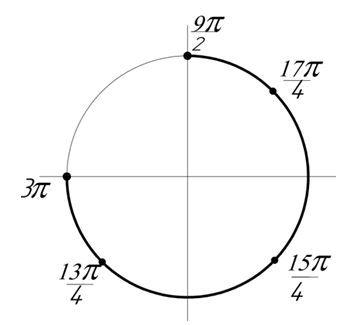
Вычислим явно все корни, принадлежащие данному отрезку.

x1 = π+ π-⋅6= 13π, 4 2 4

π- π- 15π x2 = 4 + 2 ⋅7= 4 ,

x1 = π+ π-⋅8= 17π. 4 2 4

Ответ:

а) $x = π-+ πn, n∈ ℤ 4 2$ ;
б) $13π- 15π- 17π 4 ; 4 ; 4$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 10#78009

а) Решите уравнение $log5(4sin2 x− sin2x− 2)= 0.$

б) Укажите корни данного уравнения, принадлежащие промежутку $[−2π;−1,5].$

Показать ответ и решение

По определению логарифма получаем

2 0 4 sin x− sin2x − 2= 5,

2 4sin x − sin2x− 2= 1,

2 4sin x − sin2x− 3= 0.

Воспользуемся формулой синуса двойного угла:

2 4sin x − 2sinxcosx− 3= 0.

По ОТТ:

4sin2x− 2sinxcosx− 3(sin2x+ cos2x) =0,

4sin2x− 2sin xcosx− 3sin2x − 3 cos2x =0,

sin2x − 2 sinxcosx− 3cos2x= 0.

Полученное уравнение — однородное второго порядка. Рассмотрим два случая.
1) $cosx = 0.$
Подставив значение косинуса в уравнение, получим $2 sin x = 0,$ откуда получаем, что $sinx = 0,$ а это ведет к противоречию с ОТТ. То есть в данном случае решений нет.
2) $cosx ⁄= 0.$
В этом случае можно поделить обе части уравнения на $cos2x,$ что приводит к уравнению относительно тангенса:

tg2 x− 2tgx− 3= 0.

Сделаем замену $t =tgx$ и получим квадратное уравнение:

t2− 2t− 3 = 0.

Его корнями являются $t = −1 1$ и $t= 3. 2$ Сделаем обратную замену:
1) $tg x= −1$

π x = −4-+ πn, n ∈ℤ.

tgx= 3,

x =arctg 3+ πn, n ∈ ℤ.

б) Отберём корни, принадлежащие отрезку $[− 2π;− 1,5].$ Для отбора корней воспользуемся тригонометрической окружностью:

$PIC$

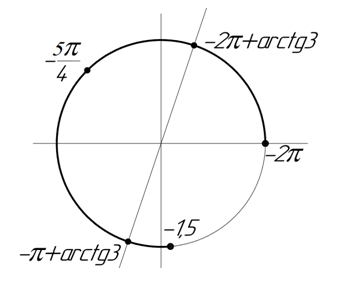
Вычислим явно все корни, принадлежащие данному отрезку.

x =− π-+π ⋅(−1)= − 5π , 1 4 4

x2 = arctg3+ π⋅(−2)= arctg3 − 2π,

x3 = arctg3 +π ⋅(− 1)= arctg3− π.

При этом принимаем во внимание, что $π- − 1,5> −2 ,$ так как $− 3> −π.$

Ответ:

а) $− π+ πn 4$ ; $arctg3+ πn$ ; $n∈ ℤ$ ;
б) $5π − 4 ;arctg3− 2π;arctg3− π$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 11#72209

а) Решите уравнение $16sinx+ 5⋅22sinx− 14 = 0.$

б) Найдите корни уравнения, принадлежащие отрезку $[3π2 ;3π].$

Показать ответ и решение

Преобразуем запись согласно свойству степеней $(ab)c = abc :$

24sinx +5 ⋅22sinx − 14 =0,

(22sinx)2 +5 ⋅22sinx − 14 = 0,

Сделаем замену $22sinx = t:$

t2 +5t− 14= 0,

D =52 − 4 ⋅1 ⋅(− 14) =25 +56 =81 = 92,

$⌊ |t = −5+-9-=2, ⌈ −5 2− 9 t= --2---= −7.$

Обратная замена:

$[ 2sinx 2 = 2, 22sinx = −7.$

Второе уравнение системы не имеет решений, поскольку показательная функция принимает только положительные значения. Рассмотрим первое уравнение:

2sinx 1 2 = 2,

2sin x= 1,

sinx= 1, 2

$⌊ π- |x = 6 + 2πn,n ∈ℤ, ⌈x= 5π + 2πn,n ∈ ℤ. 6$

б) Отберем корни методом двойных неравенств:

Первая серия:

3π π- 2 ≤ 6 +2πn ≤ 3π,

9π ≤ π+ 12πn ≤18π,

9 ≤ 1+ 12n ≤ 18,

8≤ 12n≤ 17,

-8 ≤n ≤ 17, 12 12

8- -5 12 ≤ n ≤112.

С учётом условия $n ∈ℤ$ получаем, что $n =1.$ Вычисляем корень:

x1 = π+ 2π⋅1 = 13π-. 6 6

Вторая серия:

3π ≤ 5π-+ 2πn≤ 3π, 2 6

9π ≤5π + 12πn ≤ 18π,

9 ≤ 5+ 12n ≤ 18,

4≤ 12n≤ 13,

-4 ≤n ≤ 13, 12 12

4- -1 12 ≤ n ≤112.

С учётом условия $n ∈ℤ$ получаем, что $n =1.$ Вычисляем корень:

x2 = 5π +2π ⋅1= 17π. 6 6

Ответ:

а) $x = π+ 2πk, 6$ $x = 5π+ 2πk, 6$ $k$ — целое.

б) $x = 13π, 6$ $x= 17π 6$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#42310

а) Решите уравнение $25sin5x +61+sin5x = 24sin5x +3 ⋅813+sin5x.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[5π 7π] 2-;-2 .$

Показать ответ и решение

Пусть $sin5x = t$ , тогда

25t+ 6⋅6t = 23t⋅3t+ 6 ⋅23t |:2t > 0 ⇔ 24t+ 6⋅3t = 22t⋅3t+ 6 ⋅22t = 0 ⇔ (22t− 6)(22t− 3t)= 0 ⇔ ⌊ 2t |2 = 6 |⌈( 4)t ⇔ 3 = 1 ⌊ ⌈4t = 6 t =0

Из первого равенства получаем, что $t> 1,$ что противоречит тому, что $t= sin 5x.$ Следовательно,

π sin5x= 0 ⇒ x = 5n, n∈ ℤ

б) Отберем корни с помощью неравенств.

5π≤ πn≤ 7π ⇔ 12,5 ≤ n≤ 17,5 ⇒ 2 5 2 13π 14π 16π 17π n= 13;14;15;16;17 ⇒ x = -5-;-5-;3π;-5-;-5-

Ответ:

а) $πn, n ∈ ℤ 5$

б) $13π 14π 16π 17π -5-;-5-;3π;-5-;-5-$

Ошибка.
Попробуйте повторить позже

Задача 13#23595

a) Решите уравнение $sinx sin(π+x) 5 4 + 4 = 2.$

б) Определите, какие из его корней принадлежат отрезку $[ ] 5π;4π . 2$

Показать ответ и решение

а) Сначала воспользуемся формулой приведения $sin(π+ x)= − sinx.$

Тогда исходное уравнение примет вид

5 4sinx+ 4− sinx = 2

Обозначим $t =4sinx,$ тогда

( ) 4− sinx = 4sinx −1 = t−1 = 1. t

Уравнение примет вид

$pict$

Найдем корни квадратного уравнения:

$pict$

Следовательно, получаем два решения системы:

⌊ ⌈t =2 t =0,5

Произведем обратную замену:

⌊ ⌊ ⌊ 4sinx = 2 4sinx = 412 sin x= 1 ⌈ sinx ⇔ ⌈ sinx − 1 ⇔ ⌈ 2 1 ⇔ 4 = 0,5 4 = 4 2 sin x= − 2 ⌊ π ||x = 6 + 2πk, k ∈ℤ ⌊ ||x =π − π6 + 2πk, k ∈ ℤ ⌈x = π6 + πk, k ∈ℤ ⇔ ||x =− π+ 2πk, k ∈ ℤ ⇔ x =− π +πk, k ∈ ℤ ⌈ 6 π 6 x =π + 6 + 2πk, k ∈ ℤ

б) Отберем подходящие корни при помощи неравенств.

[ ] x ∈ 5π;4π ⇔ 5π ≤x ≤ 4π 2 2

$pict$

Ответ:

а) $π- π- 6 + πk, − 6 + πk, k ∈ ℤ$

б) $17π, 19π, 23π- 6 6 6$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 14#19502

а) Решите уравнение $( ) √- (0,25)sinx cosx =2− 2sinx.$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[ ] 7π 2π;2- .$

Показать ответ и решение

а) Сведем уравнение к простейшему показательному и далее к простейшим тригонометрическим:

$pict$

б) Отберем подходящие решения с помощью тригонометрической окружности.

$PIC$

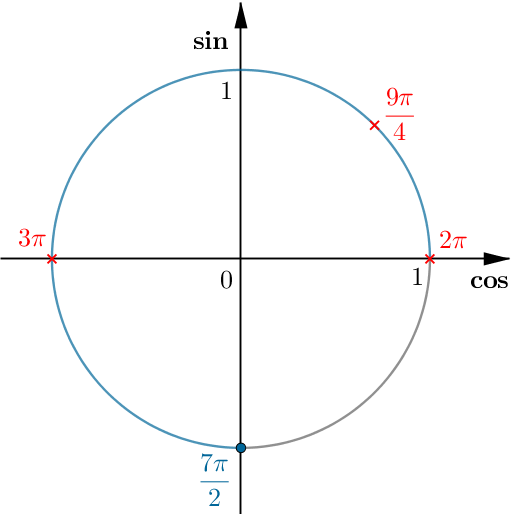
Таким образом, получим корни

9π 2π,-4 , 3π

Ответ:

а) $πk;$ $± π-+ 2πk, 4$ $k ∈ ℤ$

б) $2π,$ $9π , 4$ $3π$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 15#19501

а) Решите уравнение: $125sin2x = (√5)5sin2x ⋅0,2$ .

б) Найдите все корни этого уравнения, принадлежащие отрезку $[− 3π;− 2π]$ .

Показать ответ и решение

Решим пункт а:

$pict$

Решим пункт б, проведя отбор на единичной окружности:

$PIC$

Таким образом, получим корни $arcctg4 − 3π$ , $− 11π- 4$ .

Ответ:

а) $x = arcctg 4+ πk, k ∈ ℤ$ , $π x = 4 + πn, n ∈ ℤ$ ;

б) $arcctg4 − 3π$ , $11π-- − 4$ .

Ошибка.
Попробуйте повторить позже

Задача 16#18133

a) Решите уравнение $sinx 3cosx (27cosx) = 3 2$ .

б) Найдите все корни этого уравнения, принадлежашие отрезку $[ ] − π; π . 2$

Показать ответ и решение

а) Для начала преобразуем левую часть уравнения:

cosxsinx cosxsinx 3cosxsinx (27 ) = 27 = 3

Подставим полученное выражение в исходное уравнение:

$pict$

б) Отберем подходящие корни с помощью неравенств:

$pict$

Ответ:

а) $π π 5π 2-+ πk;-6 + 2πk;-6-+ 2πk, k ∈ ℤ$

б) $− π; π; π- 2 2 6$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Комментарий

Ответ в задании с развёрнутым ответом – это решение и вывод (называемый ответом).

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#17244

а) Решите уравнение $sinx cosx √3sinx (49 ) = 7 .$

б) Найдите его корни, принадлежащие отрезку $[ ] − 5π;− 3π . 2 2$

Показать ответ и решение

а) Сведем исходное уравнение к простейшему показательному и далее к простейшим тригонометрическим:

$pict$

б) Отберем подходящие корни неравенствами, учитывая, что $k ∈ℤ.$

5π 3π − 2 ≤ πk ≤ − 2 ⇔ −2,5 ≤k ≤ −1,5 ⇔ k = −2, x= −2π − 5π-≤ π-+ 2πk ≤ − 3π ⇔ − 15-≤ 1 +2k ≤ − 9 ⇔ 2 6 2 6 6 6 ⇔ − 8 ≤k ≤ − 5 ⇔ k = −1, x= π-− 2π = − 11π 6 6 6 6 − 5π ≤ − π-+ 2πk ≤ − 3π ⇔ − 15-≤ − 1+ 2k ≤ − 9 ⇔ 2 6 2 6 6 6 ⇔ − 7 ≤ k ≤ − 4 ⇔ k = − 1, x= − π− 2π = − 13π 6 6 6 6

Ответ:

а) $π- πk; ± 6 + 2πk, k ∈ℤ$

б) $− 2π;− 11π-;− 13π 6 6$

Критерии оценки


Содержание критерия	Балл

Обоснованно получены верные ответы в обоих пунктах	2

Обоснованно получен верный ответ в пункте а)	1
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а) и пункта б)

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2