Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции .
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика:
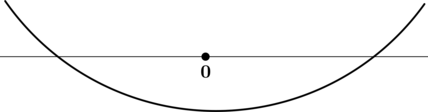
Таким образом, – точка минимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции .
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика:
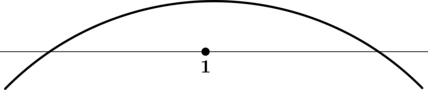
Таким образом, – точка максимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции
1 способ.
Заметим, что
Заметим, что при
2 способ.
Найдем производную функции.

Таким образом, по определению точка
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции
Найдем ОДЗ: что равносильно
откуда находим
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:
— на ОДЗ, откуда находим Для того, чтобы найти точки локального максимума/минимума функции, нужно понять,
как схематично выглядит её график.
2) Найдём промежутки знакопостоянства на ОДЗ:
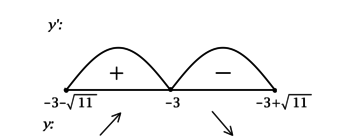
3) Эскиз графика
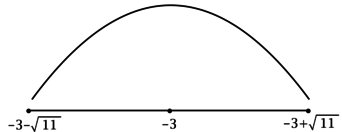
Таким образом, — точка максимума функции
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:
Отсюда на ОДЗ получаем
Далее имеем:
Тогда производная функции определена при любом
Для того, чтобы найти точки локального максимума/минимума
функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства
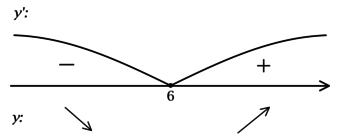
3) Эскиз графика
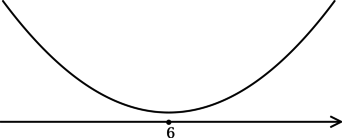
Таким образом, — точка минимума функции
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Функция является композицией двух функций
и
то есть
Так как — возрастающая функция,
убывает при
и
возрастает при
то
убывает при
и возрастает при
(так как композиция возрастающих функций — возрастающая, а
убывающей и возрастающей — убывающая).
Следовательно, — точка минимума функции
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Найдем производную заданной функции:
Легко видеть, что первый множитель определен и не равен нулю при любом
Второй множитель зануляется при
Применим метод интервалов для определения знаков производной. Критическая точка встречается ровно один раз, следовательно, в ней знак будет меняться.
Теперь можем нарисовать эскиз графика. На промежутке
производная функции
отрицательна, то есть исходная функция будет
убывать. На промежутке
производная положительна, то есть исходная
функция будет возрастать.
По эскизу видно, что точка является точкой минимума, так
как в ней производная меняет знак с «
» на «
» при проходе слева
направо.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:
Отсюда получаем и
Далее имеем:
Тогда производная определена для любого
Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства
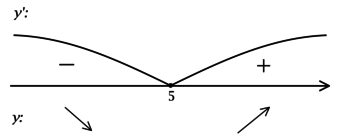
3) Эскиз графика
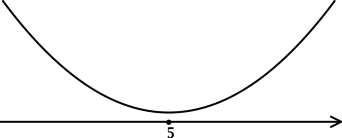
Таким образом, — точка минимума функции
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
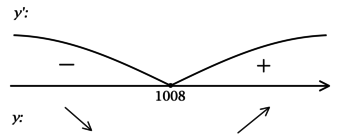
3) Эскиз графика :
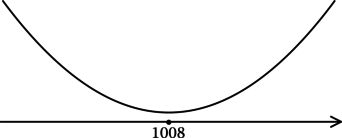
Таким образом, – точка минимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку минимума функции
Выпишем ОДЗ:
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:
Отсюда на ОДЗ получаем
Далее имеем:
Тогда производная определена для любого Для того, чтобы найти точки локального максимума/минимума функции, нужно
понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства
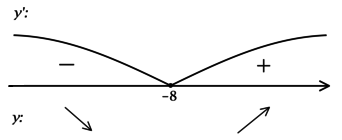
3) Эскиз графика
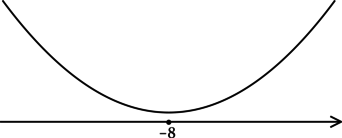
Таким образом, — точка минимума функции
Ошибка.
Попробуйте повторить позже
Найдите точку максимума функции
.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства на ОДЗ:
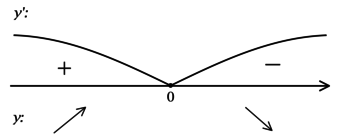
3) Эскиз графика :
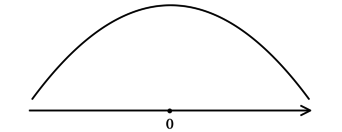
Таким образом, – точка максимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку локального максимума функции
.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
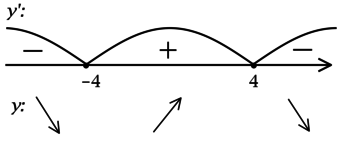
3) Эскиз графика :
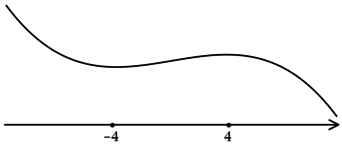
Таким образом, – точка локального максимума функции
.
Ошибка.
Попробуйте повторить позже
Найдите точку локального максимума функции , лежащую на отрезке
.
ОДЗ: – произвольный.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства (здесь бесконечно много промежутков, знаки
производной в которых чередуются):
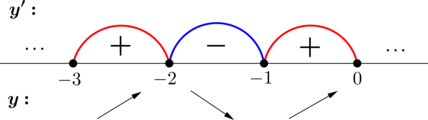
3) Найдём промежутки знакопостоянства на
:

3) Эскиз графика на
:
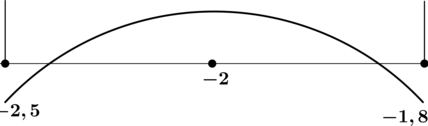
Таким образом, – точка локального максимума функции
на отрезке
.
Ошибка.
Попробуйте повторить позже
Найдите точку локального максимума функции .
ОДЗ: .
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика :
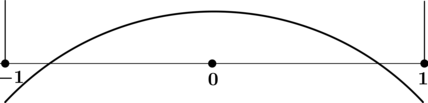
Таким образом, – точка локального максимума функции
.



